Topic square root 52 simplified: Discover the simplest method to simplify the square root of 52. In this article, we'll break down the process step-by-step, making it easy to understand and apply. Perfect for students and math enthusiasts, learn how to express √52 in its simplest form with clear explanations and examples.
Table of Content
- Simplifying the Square Root of 52
- Introduction to Square Roots
- Understanding the Concept of Simplifying Square Roots
- Prime Factorization Method
- Steps to Simplify the Square Root of 52
- Mathematical Representation of Simplified Square Roots
- Applications of Simplified Square Roots in Mathematics
- Common Mistakes to Avoid
- YOUTUBE: Hướng dẫn cách đơn giản hóa căn bậc hai của 52 để giúp bạn hiểu rõ hơn về khái niệm căn bậc hai và các phương pháp đơn giản hóa.
Simplifying the Square Root of 52
The square root of 52 can be simplified by expressing it in terms of its prime factors.
Steps to Simplify
- Find the prime factorization of 52.
- Prime factors of 52: 52 = 2 × 2 × 13.
- Pair the prime factors.
- Take one factor from each pair out of the square root.
Therefore, we have:
\[
\sqrt{52} = \sqrt{2 \times 2 \times 13} = \sqrt{2^2 \times 13} = 2\sqrt{13}
\]
Conclusion
Thus, the simplified form of the square root of 52 is \(2\sqrt{13}\).

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is a fundamental concept in mathematics, often represented by the radical symbol (√). For instance, the square root of 9 is 3 because \(3 \times 3 = 9\).
Understanding square roots involves several key points:
- The square root of a positive number has two values: a positive and a negative one. For example, the square root of 16 is both 4 and -4.
- Square roots of perfect squares are integers, such as √25 = 5.
- Non-perfect squares result in irrational numbers, like √2, which cannot be expressed as a simple fraction.
Here are some important properties of square roots:
- \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) (where b ≠ 0)
- \((\sqrt{a})^2 = a\)
Square roots are widely used in various branches of mathematics, including algebra, geometry, and calculus, and they are essential for solving quadratic equations and working with right triangles.
Understanding the Concept of Simplifying Square Roots
Simplifying square roots involves expressing a square root in its simplest form. This process makes it easier to work with square roots in mathematical expressions and equations. The goal is to identify and extract perfect square factors from under the square root.
Here are the steps to simplify square roots:
- Identify the prime factorization of the number under the square root.
- Group the prime factors into pairs of identical factors.
- Move each pair of identical factors outside the square root as a single factor.
- Multiply the factors outside the square root together, and simplify the expression inside the square root if possible.
Let's illustrate this with an example:
- Simplify \(\sqrt{72}\):
- Find the prime factorization of 72: \(72 = 2 \times 2 \times 2 \times 3 \times 3\).
- Group the prime factors into pairs: \(72 = (2 \times 2) \times (3 \times 3) \times 2\).
- Move each pair outside the square root: \(\sqrt{72} = 2 \times 3 \times \sqrt{2}\).
- Multiply the factors outside: \(\sqrt{72} = 6\sqrt{2}\).
Therefore, \(\sqrt{72}\) simplifies to \(6\sqrt{2}\).
Simplifying square roots helps in reducing the complexity of expressions and solving mathematical problems more efficiently. It is a valuable skill in algebra and higher-level mathematics.
Prime Factorization Method
The prime factorization method is a systematic approach to simplify square roots by breaking down a number into its prime factors. This method is particularly useful for identifying pairs of factors that can be extracted from under the square root.
Here are the steps to use the prime factorization method:
- Find the prime factors: Determine the prime numbers that multiply together to give the original number.
- Group the prime factors: Organize the prime factors into pairs of identical numbers.
- Simplify the square root: Move each pair of prime factors outside the square root, leaving any unpaired factors inside.
Let's apply the prime factorization method to the number 52:
- Step 1: Find the prime factors of 52:
- 52 is even, so divide by 2: \(52 \div 2 = 26\)
- 26 is even, so divide by 2: \(26 \div 2 = 13\)
- 13 is a prime number.
Thus, the prime factors of 52 are \(2 \times 2 \times 13\).
- Step 2: Group the prime factors:
Identify pairs of identical factors: \(52 = 2^2 \times 13\).
- Step 3: Simplify the square root:
Move the pair of 2's outside the square root:
\[
\sqrt{52} = \sqrt{2^2 \times 13} = 2\sqrt{13}
\]
Therefore, using the prime factorization method, \(\sqrt{52}\) simplifies to \(2\sqrt{13}\). This method helps in easily identifying and extracting perfect square factors, making it simpler to handle square roots in various mathematical problems.
Steps to Simplify the Square Root of 52
Simplifying the square root of 52 involves breaking down the number into its prime factors and then simplifying the expression by extracting perfect squares. Follow these detailed steps:
- Find the prime factorization of 52:
- 52 is an even number, so divide by 2: \(52 \div 2 = 26\)
- 26 is also even, so divide by 2 again: \(26 \div 2 = 13\)
- 13 is a prime number, so it cannot be factored further.
Thus, the prime factorization of 52 is \(2 \times 2 \times 13\), or \(2^2 \times 13\).
- Rewrite the square root using the prime factors:
Express the square root of 52 in terms of its prime factors:
\[
\sqrt{52} = \sqrt{2^2 \times 13}
\] - Extract the perfect square factor:
Since \(2^2\) is a perfect square, it can be moved outside the square root:
\[
\sqrt{2^2 \times 13} = 2\sqrt{13}
\] - Write the simplified form:
The simplified form of the square root of 52 is:
\[
\sqrt{52} = 2\sqrt{13}
\]
By following these steps, you can simplify the square root of 52 to \(2\sqrt{13}\), making it easier to handle in mathematical expressions and equations.
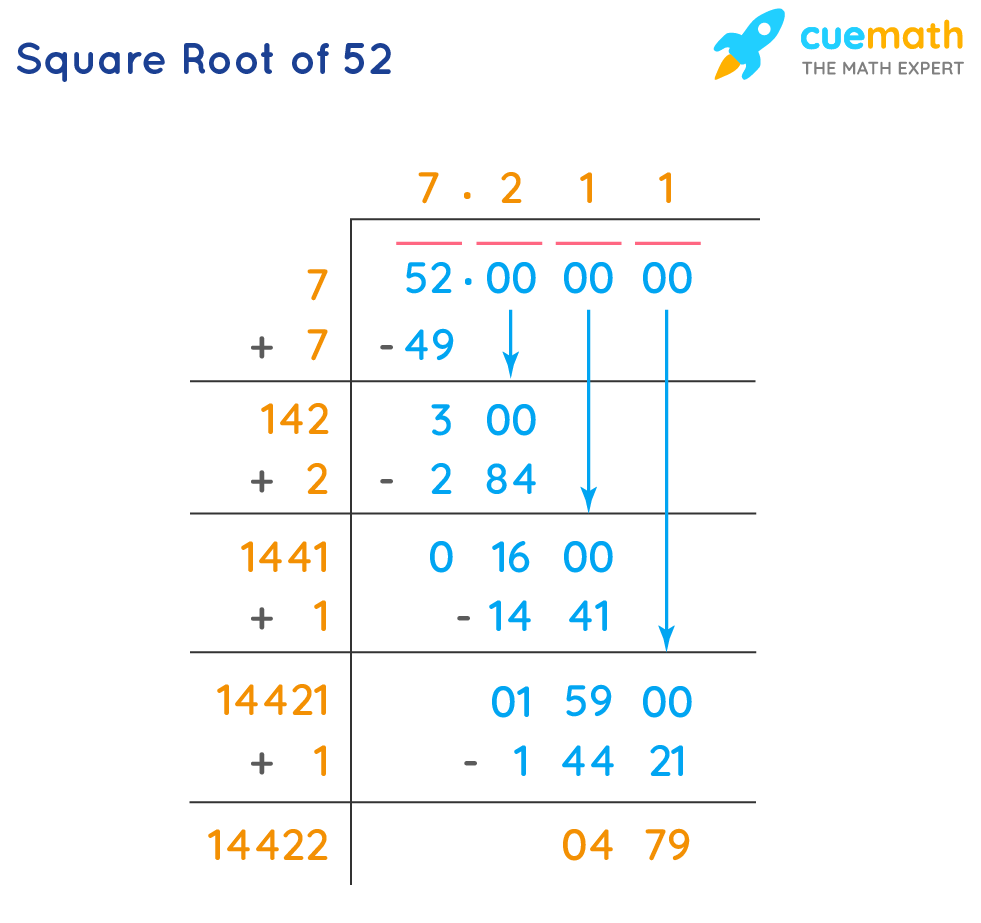
Mathematical Representation of Simplified Square Roots
In mathematics, representing square roots in their simplified form is crucial for clarity and ease of calculation. The process involves breaking down the number under the square root into its prime factors and extracting perfect squares. Here's how to represent simplified square roots mathematically:
- Identify the prime factors:
Break down the number into its prime factors. For example, for 52, the prime factorization is:
\[
52 = 2 \times 2 \times 13 = 2^2 \times 13
\] - Rewrite the square root:
Express the square root using these prime factors:
\[
\sqrt{52} = \sqrt{2^2 \times 13}
\] - Extract the perfect square factors:
Move the perfect square factors outside the square root:
\[
\sqrt{2^2 \times 13} = 2\sqrt{13}
\]
The mathematical representation of the simplified square root of 52 is:
\[
\sqrt{52} = 2\sqrt{13}
\]
This simplified form is much easier to work with in equations and mathematical expressions. Here's a comparison of different representations of square roots:
| Original Expression | Simplified Form |
|---|---|
| \(\sqrt{52}\) | \(2\sqrt{13}\) |
| \(\sqrt{72}\) | \(6\sqrt{2}\) |
| \(\sqrt{18}\) | \(3\sqrt{2}\) |
By simplifying square roots, we make calculations more straightforward and expressions more concise, enhancing our ability to solve mathematical problems efficiently.
Applications of Simplified Square Roots in Mathematics
Simplified square roots play a vital role in various mathematical concepts and applications. By simplifying square roots, we can streamline calculations, solve equations more efficiently, and better understand mathematical relationships. Here are some key applications of simplified square roots in mathematics:
- Solving Quadratic Equations:
Quadratic equations often involve square roots in their solutions. Simplifying these roots helps in finding the roots of the equation more easily. For example, the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]requires simplifying the discriminant \(\sqrt{b^2 - 4ac}\) to find the solutions for \(x\).
- Geometry and Trigonometry:
Simplified square roots are essential in geometry and trigonometry for calculating distances, areas, and angles. For instance, the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2}
\]where \(c\) is the hypotenuse of a right triangle, often involves simplifying the square root to find the length of \(c\).
- Algebraic Manipulations:
Simplifying square roots allows for easier manipulation and simplification of algebraic expressions. This is crucial when adding, subtracting, or multiplying expressions involving square roots.
- Calculus:
In calculus, simplified square roots are used in differentiation and integration. For example, integrating functions that include square roots often requires simplifying the integrand first.
- Physics and Engineering:
Simplified square roots are frequently used in physics and engineering to solve problems involving motion, forces, and energy. These fields often require precise calculations where simplified square roots can make a significant difference.
Overall, the ability to simplify square roots is a fundamental skill in mathematics that enhances problem-solving capabilities across various disciplines, making complex calculations more manageable and comprehensible.
Common Mistakes to Avoid
When simplifying the square root of 52, it's important to watch out for these common errors:
- Incorrect Prime Factorization: Ensure that the prime factorization of 52 is correct. Mistakes in this step can lead to incorrect simplification.
- Misinterpreting Square Root Properties: Understand the properties of square roots correctly. Errors here can result in incorrect simplification steps.
- Skipping Steps: Each step in the simplification process is crucial. Skipping steps may lead to overlooking factors or making computational errors.
- Not Verifying Results: Always double-check your simplified square root to ensure it is accurate. Small mistakes can easily go unnoticed but affect the final result.
- Confusing Addition with Multiplication: In some cases, confusion between addition and multiplication when combining factors can lead to incorrect simplification.
By avoiding these common mistakes and following the correct procedures, you can ensure accurate and reliable simplification of the square root of 52.
Hướng dẫn cách đơn giản hóa căn bậc hai của 52 để giúp bạn hiểu rõ hơn về khái niệm căn bậc hai và các phương pháp đơn giản hóa.
How to Simplify the Square Root of 52: Sqrt(52)
READ MORE:
Hướng dẫn chi tiết cách đơn giản hóa căn bậc hai của số 52, giúp bạn hiểu rõ hơn về các phương pháp đơn giản hóa và ứng dụng trong toán học.
Làm thế nào để đơn giản hóa căn bậc hai của 52?















