Topic square roots simplified: Welcome to our ultimate guide on simplifying square roots. This comprehensive article will help you master the basics, understand the step-by-step process, and apply advanced techniques. Whether you're a student or a math enthusiast, you'll find valuable insights and practical examples to simplify square roots with confidence.
Table of Content
- Square Roots Simplified
- Introduction to Square Roots
- Basic Concepts and Definitions
- How to Simplify Square Roots
- Step-by-Step Simplification Process
- Prime Factorization Method
- Identifying Perfect Squares
- Examples of Simplifying Square Roots
- Special Cases and Common Mistakes
- Practice Problems and Solutions
- Advanced Techniques and Tips
- Applications of Simplified Square Roots
- Additional Resources and References
- Conclusion
- YOUTUBE: Hãy xem video 'Hướng dẫn Cách Rút Gọn Căn Bậc Hai' để học cách đơn giản hóa các căn bậc hai và áp dụng vào các bài toán thực tế.
Square Roots Simplified
Square roots can often be simplified to make them easier to work with. The process involves factoring the number inside the square root to find perfect squares.
Steps to Simplify Square Roots
- Factor the number inside the square root into its prime factors.
- Identify and separate the perfect squares from the prime factors.
- Take the square root of the perfect squares and move them outside the square root.
- Multiply the numbers outside the square root.
- Leave the remaining factors inside the square root.
Examples
Here are some examples of simplifying square roots:
Example 1:
\(\sqrt{18}\)
Factor 18 into \(2 \times 3^2\).
\(\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}\)
Example 2:
\(\sqrt{50}\)
Factor 50 into \(2 \times 5^2\).
\(\sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2}\)
Example 3:
\(\sqrt{72}\)
Factor 72 into \(2^3 \times 3^2\).
\(\sqrt{72} = \sqrt{2^3 \times 3^2} = 3\sqrt{8} = 3\sqrt{4 \times 2} = 3 \times 2\sqrt{2} = 6\sqrt{2}\)
Practice Problems
Try simplifying the following square roots:
- \(\sqrt{24}\)
- \(\sqrt{32}\)
- \(\sqrt{45}\)
- \(\sqrt{98}\)
Common Mistakes
- Forgetting to factor the number completely.
- Not identifying all the perfect squares.
- Incorrectly simplifying the square root of a non-perfect square.
Additional Tips
- Always double-check your factors to ensure accuracy.
- Practice with different numbers to become more familiar with the process.
- Remember that not all square roots can be simplified (e.g., \(\sqrt{2}\), \(\sqrt{3}\)).

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. Square roots are fundamental in mathematics and are symbolized by the radical sign (√). Understanding square roots is essential for solving various mathematical problems and is widely used in algebra, geometry, and real-world applications.
For example, the square root of 16 is 4 because \( 4 \times 4 = 16 \). Similarly, the square root of 25 is 5 because \( 5 \times 5 = 25 \).
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are integers.
- Non-Perfect Squares: Numbers like 2, 3, 5, and 7 are not perfect squares, and their square roots are irrational numbers.
Here are some key concepts related to square roots:
- Principal Square Root: The non-negative square root of a number. For example, the principal square root of 9 is 3.
- Radical Sign: The symbol used to denote the square root, written as √.
- Radicand: The number under the radical sign. For instance, in √25, 25 is the radicand.
Understanding square roots involves recognizing both perfect and non-perfect squares and learning methods to simplify square roots. Let's delve deeper into these concepts to build a strong foundation in simplifying square roots.
Basic Concepts and Definitions
Square roots are fundamental concepts in mathematics, representing a value that, when multiplied by itself, gives the original number. Understanding square roots is essential for various mathematical applications and problem-solving techniques. Below are the key concepts and definitions related to square roots:
- Square Root (\(\sqrt{}\)): The square root of a number \(x\) is a value \(y\) such that \(y \times y = x\). It is denoted as \(\sqrt{x}\).
- Radicand: The number under the square root symbol. For \(\sqrt{x}\), \(x\) is the radicand.
- Perfect Squares: Numbers that have integer square roots. Examples include 1, 4, 9, 16, 25, etc.
- Irrational Numbers: Square roots of non-perfect squares are often irrational numbers, meaning they cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions.
- Principal Square Root: The non-negative square root of a number. For example, \(\sqrt{25} = 5\) and not \(-5\).
- Negative Square Roots: While the square of both positive and negative numbers can be positive, by convention, \(\sqrt{x}\) refers to the principal (positive) square root. However, \(-\sqrt{x}\) represents the negative square root.
To further illustrate these concepts, consider the following table:
| Number | Square Root | Perfect Square? | Notes |
|---|---|---|---|
| 1 | \(\sqrt{1} = 1\) | Yes | 1 is a perfect square because \(1 \times 1 = 1\). |
| 2 | \(\sqrt{2} \approx 1.414\) | No | 2 is not a perfect square; its square root is irrational. |
| 4 | \(\sqrt{4} = 2\) | Yes | 4 is a perfect square because \(2 \times 2 = 4\). |
| 9 | \(\sqrt{9} = 3\) | Yes | 9 is a perfect square because \(3 \times 3 = 9\). |
| 10 | \(\sqrt{10} \approx 3.162\) | No | 10 is not a perfect square; its square root is irrational. |
Understanding these basic concepts and definitions of square roots provides a strong foundation for further exploration and simplification techniques.
How to Simplify Square Roots
Simplifying square roots involves expressing a square root in its simplest form. This process reduces the number inside the square root to the smallest possible whole number, making it easier to work with in calculations.
To simplify a square root, follow these steps:
- Factor the Number: Break down the number inside the square root into its prime factors. For example, for √18, we factor 18 into 2 × 3 × 3.
- Identify Perfect Squares: Look for pairs of prime factors. In our example, 18 factors into 2 × 3 × 3. Here, 3 × 3 forms a perfect square.
- Rewrite the Expression: Rewrite the square root as the product of square roots, separating the perfect squares. For √18, we get √(9 × 2).
- Simplify: Take the square root of the perfect square and multiply it by the remaining square root. Thus, √(9 × 2) becomes 3√2.
Let's look at some examples:
- Example 1: Simplify √12
- Factor 12 into 4 × 3
- Rewrite as √(4 × 3)
- Simplify to 2√3 (since √4 = 2)
- Example 2: Simplify √45
- Factor 45 into 9 × 5
- Rewrite as √(9 × 5)
- Simplify to 3√5 (since √9 = 3)
You can also simplify the product and quotient of square roots:
- Product Rule: √a × √b = √(a × b)
- Example: √12 × √3 = √(12 × 3) = √36 = 6
- Quotient Rule: √(a/b) = √a / √b
- Example: √(25/4) = √25 / √4 = 5 / 2
With these methods, you can simplify any square root to its simplest form, making calculations and further operations much easier.
Step-by-Step Simplification Process
Simplifying square roots involves breaking down the number inside the square root into its prime factors and using properties of square roots to simplify. Follow these steps for a clear process:
-
Factorize the Number: Begin by finding the prime factors of the number under the square root. For example, to simplify \(\sqrt{72}\), first find the prime factors:
72 = 2 × 2 × 2 × 3 × 3
-
Pair the Factors: Group the prime factors into pairs. Each pair of identical factors can be taken out of the square root. For \(\sqrt{72}\), pair the factors:
72 = (2 × 2) × (2) × (3 × 3)
-
Take Out the Pairs: For every pair, take one factor out of the square root. For \(\sqrt{72}\):
\(\sqrt{72} = \sqrt{(2 × 2) × (3 × 3) × 2} = 2 × 3 × \sqrt{2} = 6\sqrt{2}\)
Another method involves identifying the largest perfect square factor of the number:
-
Identify Perfect Square Factors: List all factors of the number and identify the largest perfect square. For \(\sqrt{72}\), the factors are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, and 72. The largest perfect square is 36.
-
Rewrite the Radical: Express the number as a product of the perfect square and another factor. For \(\sqrt{72}\):
72 = 36 × 2
-
Separate and Simplify: Use the property \(\sqrt{ab} = \sqrt{a} × \sqrt{b}\) to split the radical and simplify. For \(\sqrt{72}\):
\(\sqrt{72} = \sqrt{36 × 2} = \sqrt{36} × \sqrt{2} = 6\sqrt{2}\)
Using these steps will help simplify square roots effectively, making complex expressions easier to work with.
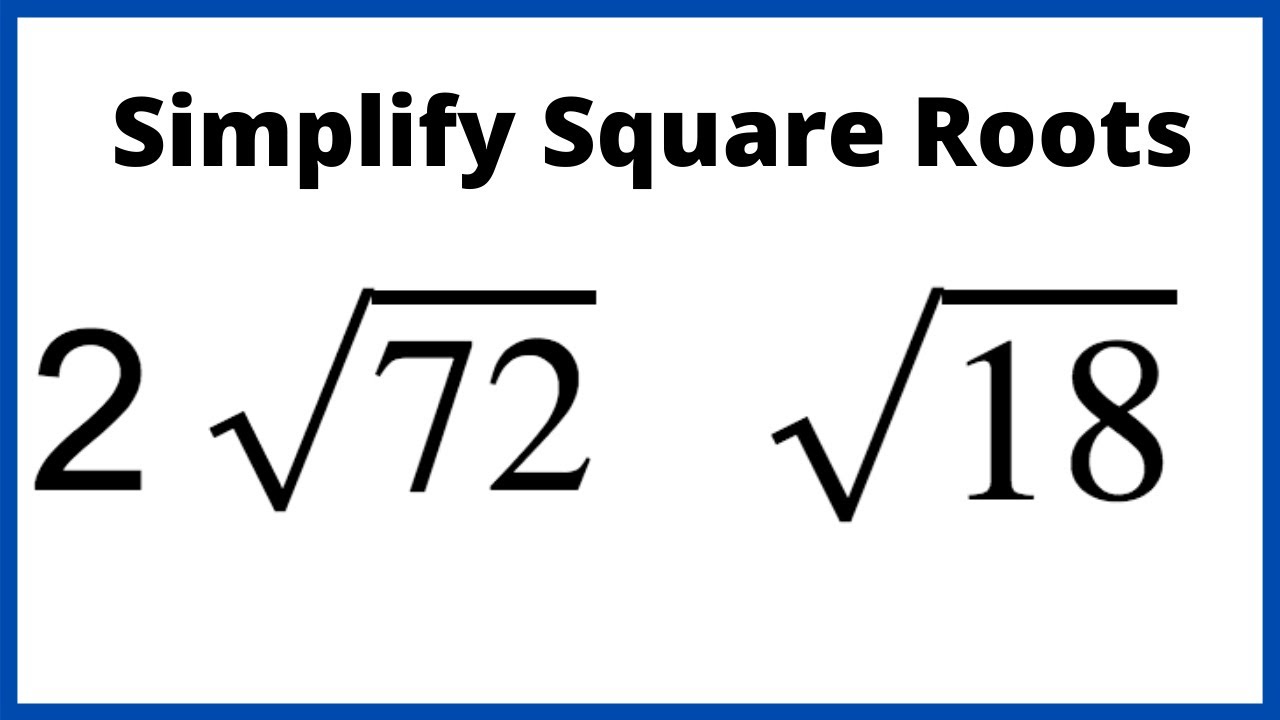
Prime Factorization Method
The prime factorization method is a straightforward approach to simplifying square roots by breaking down the number into its prime factors. Here’s how you can use this method step-by-step:
-
Find the Prime Factors: Begin by finding the prime factors of the number under the square root. Prime factors are the prime numbers that multiply together to give the original number.
For example, to simplify \( \sqrt{72} \):
- Divide 72 by the smallest prime number, 2: \( 72 \div 2 = 36 \)
- Divide 36 by 2: \( 36 \div 2 = 18 \)
- Divide 18 by 2: \( 18 \div 2 = 9 \)
- Divide 9 by the next smallest prime number, 3: \( 9 \div 3 = 3 \)
- Divide 3 by 3: \( 3 \div 3 = 1 \)
- So, the prime factors of 72 are \( 2 \times 2 \times 2 \times 3 \times 3 \)
-
Group the Prime Factors: Pair the prime factors into groups of two. Each pair of the same number can be taken out of the square root.
For \( \sqrt{72} \):
- Group the factors: \( (2 \times 2) \times (3 \times 3) \times 2 \)
- Each pair comes out of the square root as a single number: \( 2 \) and \( 3 \)
-
Simplify: Multiply the numbers outside the square root and leave any unpaired factors inside the square root.
For \( \sqrt{72} \):
- Take the pairs out: \( 2 \times 3 \)
- Multiply them: \( 2 \times 3 = 6 \)
- What’s left inside the square root is the unpaired factor: \( \sqrt{2} \)
- So, \( \sqrt{72} = 6\sqrt{2} \)
In summary, the prime factorization method involves breaking down the number into its prime factors, grouping the factors into pairs, taking out the pairs, and simplifying the expression.
Identifying Perfect Squares
Identifying perfect squares is an essential step in simplifying square roots. A perfect square is a number that can be expressed as the product of an integer with itself. Here’s how you can identify and work with perfect squares step-by-step:
-
Understand the Definition: A perfect square is any integer \( n \) that can be written as \( k^2 \), where \( k \) is also an integer.
For example, \( 1, 4, 9, 16, 25, \ldots \) are perfect squares because:
- \( 1 = 1^2 \)
- \( 4 = 2^2 \)
- \( 9 = 3^2 \)
- \( 16 = 4^2 \)
- \( 25 = 5^2 \)
-
Recognize Common Perfect Squares: It helps to memorize common perfect squares to quickly identify them. Here are some to remember:
- \( 1^2 = 1 \)
- \( 2^2 = 4 \)
- \( 3^2 = 9 \)
- \( 4^2 = 16 \)
- \( 5^2 = 25 \)
- \( 6^2 = 36 \)
- \( 7^2 = 49 \)
- \( 8^2 = 64 \)
- \( 9^2 = 81 \)
- \( 10^2 = 100 \)
-
Identify Perfect Squares in Square Roots: When simplifying square roots, look for factors that are perfect squares.
For example, to simplify \( \sqrt{50} \):
- Break down 50 into factors: \( 50 = 25 \times 2 \)
- Recognize that 25 is a perfect square: \( 25 = 5^2 \)
- Use this to simplify: \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \)
-
Practice with Larger Numbers: For larger numbers, it’s useful to perform prime factorization and look for pairs of the same number, which indicate perfect squares.
For example, to simplify \( \sqrt{200} \):
- Break down 200 into prime factors: \( 200 = 2 \times 2 \times 2 \times 5 \times 5 \)
- Group the factors: \( (2 \times 2) \times (5 \times 5) \times 2 \)
- Recognize perfect squares: \( 4 = 2^2 \) and \( 25 = 5^2 \)
- Simplify: \( \sqrt{200} = \sqrt{4 \times 25 \times 2} = \sqrt{4} \times \sqrt{25} \times \sqrt{2} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2} \)
By understanding and identifying perfect squares, you can simplify square roots more effectively and accurately.
Examples of Simplifying Square Roots
To better understand the process of simplifying square roots, let's go through several examples step-by-step.
-
Example 1: Simplify \( \sqrt{18} \)
- Step 1: Find the prime factors of 18.
- \( 18 = 2 \times 3 \times 3 \)
- Step 2: Group the prime factors into pairs.
- \( 18 = 2 \times (3 \times 3) \)
- Step 3: Take out the pairs from under the square root.
- \( \sqrt{18} = \sqrt{2 \times (3 \times 3)} = 3\sqrt{2} \)
-
Example 2: Simplify \( \sqrt{50} \)
- Step 1: Find the prime factors of 50.
- \( 50 = 2 \times 5 \times 5 \)
- Step 2: Group the prime factors into pairs.
- \( 50 = 2 \times (5 \times 5) \)
- Step 3: Take out the pairs from under the square root.
- \( \sqrt{50} = \sqrt{2 \times (5 \times 5)} = 5\sqrt{2} \)
-
Example 3: Simplify \( \sqrt{72} \)
- Step 1: Find the prime factors of 72.
- \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \)
- Step 2: Group the prime factors into pairs.
- \( 72 = (2 \times 2) \times (3 \times 3) \times 2 \)
- Step 3: Take out the pairs from under the square root.
- \( \sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \sqrt{2} = 6\sqrt{2} \)
-
Example 4: Simplify \( \sqrt{98} \)
- Step 1: Find the prime factors of 98.
- \( 98 = 2 \times 7 \times 7 \)
- Step 2: Group the prime factors into pairs.
- \( 98 = 2 \times (7 \times 7) \)
- Step 3: Take out the pairs from under the square root.
- \( \sqrt{98} = \sqrt{2 \times (7 \times 7)} = 7\sqrt{2} \)
-
Example 5: Simplify \( \sqrt{144} \)
- Step 1: Recognize that 144 is a perfect square.
- \( 144 = 12 \times 12 \)
- Step 2: Simplify using the perfect square.
- \( \sqrt{144} = 12 \)
These examples illustrate the steps to simplify square roots using prime factorization and recognizing perfect squares. By practicing these steps, you can become more proficient in simplifying square roots.
Special Cases and Common Mistakes
When simplifying square roots, certain special cases and common mistakes frequently occur. Understanding these can help avoid errors and improve mathematical accuracy.
Special Cases
-
Square Roots of Perfect Squares: A perfect square is a number that has an integer as its square root. For example, the square root of 16 is 4 because \(16 = 4^2\). Recognizing perfect squares can simplify the process significantly.
\(\sqrt{4} = 2\) \(\sqrt{9} = 3\) \(\sqrt{16} = 4\) \(\sqrt{25} = 5\) \(\sqrt{36} = 6\) \(\sqrt{49} = 7\) -
Square Roots of Fractions: The square root of a fraction can be simplified using the quotient rule \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\). For example:
- \(\sqrt{\frac{16}{9}} = \frac{\sqrt{16}}{\sqrt{9}} = \frac{4}{3}\)
Common Mistakes
- Not Simplifying Completely: Failing to recognize further simplification can lead to incomplete answers. For instance, \(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \cdot \sqrt{2} = 3\sqrt{2}\). Here, the initial simplification to \(3\sqrt{2}\) is often missed.
- Misapplying the Product Rule: Incorrectly using \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) can lead to errors. For example, \(\sqrt{12} \neq \sqrt{4} \cdot \sqrt{3}\), but \(\sqrt{12} = \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3} = 2\sqrt{3}\).
- Forgetting to Rationalize the Denominator: When simplifying expressions with square roots in the denominator, it's crucial to rationalize the denominator. For example, \(\frac{1}{\sqrt{2}}\) should be rationalized to \(\frac{\sqrt{2}}{2}\).
-
Overlooking Prime Factorization: Prime factorization can simplify square roots significantly. For example, to simplify \(\sqrt{50}\):
- Factor 50 into prime factors: \(50 = 2 \times 5^2\)
- Apply the square root: \(\sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2}\)
By recognizing these special cases and avoiding common mistakes, the process of simplifying square roots becomes more manageable and accurate.

Practice Problems and Solutions
Below are several practice problems designed to help you understand how to simplify square roots. Follow the steps carefully and verify your answers.
Problem 1
Simplify \( \sqrt{50} \).
- Find the largest perfect square factor of 50.
- The largest perfect square factor of 50 is 25, because \( 25 \times 2 = 50 \).
- Rewrite the square root as a product of the square root of the perfect square and the remaining factor.
- \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} \)
- Simplify the expression.
- \( \sqrt{25} \times \sqrt{2} = 5 \sqrt{2} \)
So, \( \sqrt{50} = 5 \sqrt{2} \).
Problem 2
Simplify \( \sqrt{72} \).
- Find the largest perfect square factor of 72.
- The largest perfect square factor of 72 is 36, because \( 36 \times 2 = 72 \).
- Rewrite the square root as a product of the square root of the perfect square and the remaining factor.
- \( \sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} \)
- Simplify the expression.
- \( \sqrt{36} \times \sqrt{2} = 6 \sqrt{2} \)
So, \( \sqrt{72} = 6 \sqrt{2} \).
Problem 3
Simplify \( \sqrt{32x^2} \).
- Find the largest perfect square factor of 32 and the variable factor.
- The largest perfect square factor of 32 is 16, because \( 16 \times 2 = 32 \).
- The variable factor \( x^2 \) is already a perfect square.
- Rewrite the square root as a product of the square root of the perfect square and the remaining factor.
- \( \sqrt{32x^2} = \sqrt{16 \times 2 \times x^2} = \sqrt{16} \times \sqrt{2} \times \sqrt{x^2} \)
- Simplify the expression.
- \( \sqrt{16} \times \sqrt{2} \times \sqrt{x^2} = 4 \times \sqrt{2} \times x = 4x \sqrt{2} \)
So, \( \sqrt{32x^2} = 4x \sqrt{2} \).
Problem 4
Simplify \( \sqrt{18y^3} \).
- Find the largest perfect square factor of 18 and the variable factor.
- The largest perfect square factor of 18 is 9, because \( 9 \times 2 = 18 \).
- The largest perfect square factor of \( y^3 \) is \( y^2 \), because \( y^2 \times y = y^3 \).
- Rewrite the square root as a product of the square root of the perfect square and the remaining factor.
- \( \sqrt{18y^3} = \sqrt{9 \times 2 \times y^2 \times y} = \sqrt{9} \times \sqrt{2} \times \sqrt{y^2} \times \sqrt{y} \)
- Simplify the expression.
- \( \sqrt{9} \times \sqrt{2} \times \sqrt{y^2} \times \sqrt{y} = 3 \times \sqrt{2} \times y \times \sqrt{y} = 3y \sqrt{2y} \)
So, \( \sqrt{18y^3} = 3y \sqrt{2y} \).
Problem 5
Simplify \( \sqrt{8a^4b^2} \).
- Find the largest perfect square factor of 8 and the variable factors.
- The largest perfect square factor of 8 is 4, because \( 4 \times 2 = 8 \).
- The variable factor \( a^4 \) is already a perfect square.
- The variable factor \( b^2 \) is already a perfect square.
- Rewrite the square root as a product of the square root of the perfect square and the remaining factor.
- \( \sqrt{8a^4b^2} = \sqrt{4 \times 2 \times a^4 \times b^2} = \sqrt{4} \times \sqrt{2} \times \sqrt{a^4} \times \sqrt{b^2} \)
- Simplify the expression.
- \( \sqrt{4} \times \sqrt{2} \times \sqrt{a^4} \times \sqrt{b^2} = 2 \times \sqrt{2} \times a^2 \times b = 2a^2b \sqrt{2} \)
So, \( \sqrt{8a^4b^2} = 2a^2b \sqrt{2} \).
Advanced Techniques and Tips
When simplifying square roots, there are several advanced techniques that can help you work more efficiently and understand the underlying principles better. Below are some advanced tips and methods to enhance your skills in simplifying square roots.
- Rationalizing the Denominator:
- Simplifying Radicals Involving Variables:
- Using Conjugates:
- Combining Like Terms:
- Decomposing Complex Radicals:
- Square Root of Sums and Differences:
- Utilizing the Pythagorean Theorem:
- Advanced Factoring Techniques:
Sometimes, square roots appear in the denominator of a fraction. To simplify such expressions, you can rationalize the denominator by multiplying both the numerator and the denominator by the square root that appears in the denominator. For example:
\[
\frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}
\]
When variables are involved under the square root, treat them as you would numbers. Apply the property \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\). For example:
\[
\sqrt{18x^2} = \sqrt{18} \cdot \sqrt{x^2} = 3\sqrt{2} \cdot x = 3x\sqrt{2}
\]
To simplify expressions involving the sum or difference of square roots, use the conjugate. For example, to simplify \(\frac{1}{\sqrt{a} + \sqrt{b}}\), multiply by the conjugate \(\sqrt{a} - \sqrt{b}\):
\[
\frac{1}{\sqrt{a} + \sqrt{b}} \cdot \frac{\sqrt{a} - \sqrt{b}}{\sqrt{a} - \sqrt{b}} = \frac{\sqrt{a} - \sqrt{b}}{a - b}
\]
When dealing with expressions that contain multiple square roots, combine like terms where possible. For example:
\[
2\sqrt{3} + 3\sqrt{3} = 5\sqrt{3}
\]
Break down more complex square roots into simpler components. For example:
\[
\sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}
\]
Understand that \(\sqrt{a + b}\) is not equal to \(\sqrt{a} + \sqrt{b}\). Instead, simplify each part separately when possible:
\[
\sqrt{9 + 16} = \sqrt{25} = 5 \neq \sqrt{9} + \sqrt{16} = 3 + 4 = 7
\]
In geometry problems, the Pythagorean Theorem can help simplify square roots. For example, in a right triangle with sides \(a\), \(b\), and hypotenuse \(c\):
\[
c = \sqrt{a^2 + b^2}
\]
Use advanced factoring to simplify more complicated expressions. For example, if you encounter \(\sqrt{x^4 - 4x^2 + 4}\), recognize it as a perfect square trinomial:
\[
\sqrt{x^4 - 4x^2 + 4} = \sqrt{(x^2 - 2)^2} = x^2 - 2
\]
By mastering these advanced techniques, you will be better equipped to handle a wide variety of problems involving square roots.
Applications of Simplified Square Roots
Simplified square roots have numerous applications in various fields. Here, we explore some practical uses:
1. Geometry and Area Calculations
One of the most common applications of square roots is in geometry, particularly in calculating areas and side lengths:
- Finding the Side of a Square: If you know the area of a square, you can find the length of one side by taking the square root of the area.
2. Physics and Engineering
Square roots are frequently used in physics and engineering calculations:
- Velocity and Kinetic Energy: The relationship between velocity (v) and kinetic energy (KE) involves square roots:
- Wave Mechanics: The speed of waves in a medium can be determined using square roots:
3. Finance and Economics
Square roots are also useful in finance, particularly in calculating interest rates and volatility:
- Compound Interest: The future value of an investment can involve square roots in the formula:
- Risk Assessment: The standard deviation of investment returns, a measure of risk, often involves taking the square root of the variance.
4. Biology and Medicine
In biological and medical sciences, square roots can be used to model growth patterns and analyze data:
- Population Studies: Estimating population growth often uses square roots to calculate rates and trends.
- Dosage Calculations: Certain medication dosages are determined using formulas involving square roots to ensure safe and effective treatment.
5. Computer Science and Cryptography
In computer algorithms and cryptographic systems, square roots play a crucial role:
- Algorithm Complexity: The time complexity of certain algorithms, such as those used in searching and sorting, can involve square roots.
- Encryption Techniques: Cryptographic methods, including RSA encryption, use square roots in the generation and analysis of keys.
By understanding and applying simplified square roots, we can solve complex problems across various disciplines more effectively.
Additional Resources and References
For further learning and practice on simplifying square roots, the following resources are highly recommended:
-
Khan Academy: An extensive collection of videos and exercises on simplifying square roots, including practice problems and step-by-step tutorials.
-
Mathematics LibreTexts: Detailed explanations and examples for simplifying and using square roots, including how to handle variable expressions and approximate square roots.
-
Third Space Learning: Guides and examples for simplifying radicals, including integer and variable expressions, with a focus on practical applications and solving techniques.
-
Paul's Online Math Notes: Comprehensive notes on algebra topics, including radical expressions and their simplification, with plenty of practice problems.
These resources provide a mix of theoretical explanations, practical examples, and exercises to deepen your understanding of simplifying square roots. They are suitable for learners at different levels, from beginners to those looking to refine their skills.

Conclusion
Understanding how to simplify square roots is a foundational skill in mathematics, applicable across various fields from algebra to physics. Mastery of these techniques not only enhances problem-solving abilities but also fosters a deeper understanding of numerical relationships and patterns.
Throughout this comprehensive guide, we have explored:
- The fundamental definitions and concepts of square roots.
- Step-by-step processes for simplifying square roots using prime factorization and identifying perfect squares.
- Special cases and common mistakes to avoid when simplifying square roots.
- Practice problems with detailed solutions to reinforce learning.
- Advanced techniques and practical applications of simplified square roots.
By practicing the methods outlined and engaging with the examples provided, readers can develop confidence in handling square roots effectively. Remember, the journey to mastering mathematics is continuous, and each new concept builds upon previous knowledge.
For further exploration, additional resources and references are available to delve deeper into specific topics or to seek clarification on complex scenarios.
Thank you for exploring the world of simplified square roots with us. Embrace the challenges and enjoy the rewards of mathematical discovery!
Hãy xem video 'Hướng dẫn Cách Rút Gọn Căn Bậc Hai' để học cách đơn giản hóa các căn bậc hai và áp dụng vào các bài toán thực tế.
Hướng dẫn Cách Rút Gọn Căn Bậc Hai
READ MORE:
Xem video 'Đơn giản hóa căn bậc hai | Chỉ số mũ, căn bậc hai và ký hiệu khoa học | Tiền đề Algebra | Khan Academy' để học về cách đơn giản hóa căn bậc hai và ứng dụng trong bài toán toán học cơ bản.
Đơn giản hóa căn bậc hai | Chỉ số mũ, căn bậc hai và ký hiệu khoa học | Tiền đề Algebra | Khan Academy















