Topic simplify the square root of 85: Welcome to our comprehensive guide on how to simplify the square root of 85. Whether you're a student brushing up on math skills or just curious, this article will walk you through the steps, methods, and tips for understanding and simplifying √85 effectively. Let's make this math concept easy and clear!
Table of Content
- Simplification of the Square Root of 85
- Introduction to Square Roots
- Understanding Simplification of Square Roots
- Checking for Perfect Squares
- Step-by-Step Simplification of √85
- Approximate Value of √85
- Applications of Simplifying Square Roots
- Common Mistakes to Avoid
- Practice Problems
- Conclusion
- YOUTUBE: Video này hướng dẫn cách đơn giản hóa căn bậc hai của 85, giúp bạn nắm vững kiến thức toán học một cách dễ dàng và hiệu quả.
Simplification of the Square Root of 85
To simplify the square root of 85, we need to determine if 85 can be broken down into smaller square roots. However, 85 is not a perfect square, and it doesn't have any square factors.
Prime Factorization Method
We start by finding the prime factors of 85:
- 85 is divisible by 5, which is a prime number.
- 85 ÷ 5 = 17, and 17 is also a prime number.
So, the prime factorization of 85 is 5 × 17.
Since 85 does not have any square factors, it cannot be simplified further.
Result
The square root of 85 in its simplest form is:
$$\sqrt{85}$$
This expression cannot be simplified further.
Approximate Value
The approximate decimal value of the square root of 85 is:
$$\sqrt{85} \approx 9.219544457292887$$
This approximation can be useful for practical calculations.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because 3 × 3 = 9. This is denoted as √9 = 3.
Square roots are fundamental in mathematics and appear in various areas such as algebra, geometry, and calculus. Understanding how to simplify square roots is essential for solving complex mathematical problems efficiently.
Let's take a closer look at some basic properties of square roots:
- Positive and Negative Roots: Every positive number has two square roots, one positive and one negative. For instance, the square roots of 25 are 5 and -5.
- Perfect Squares: A perfect square is an integer that is the square of another integer. Examples include 1, 4, 9, 16, and 25.
- Non-Perfect Squares: These are numbers that do not have an integer as their square root. For example, 2, 3, 5, and 85 are non-perfect squares.
To simplify the square root of a number means to express it in its simplest radical form. This involves factoring the number under the square root and reducing it as much as possible. In the following sections, we will explore methods such as prime factorization and checking for perfect squares to simplify square roots effectively.
Understanding Simplification of Square Roots
Simplifying square roots involves expressing the square root in its simplest form. This process helps in making calculations easier and understanding the values more intuitively. Let's break down the simplification process step by step:
The general approach to simplifying square roots involves the following steps:
- Prime Factorization: Find the prime factors of the number under the square root.
- Pairing Prime Factors: Group the prime factors into pairs.
- Extracting Pairs: Move each pair of prime factors out from under the square root.
- Multiplying Remaining Factors: Multiply the factors outside the square root and the factors remaining inside.
Let's illustrate this with a general example before applying it to :
- Example: Simplify .
- Step 1: Prime factorize 72:
- Step 2: Group the prime factors into pairs:
- Step 3: Extract the pairs:
By following these steps, we can simplify square roots effectively. Now, let's apply this method to simplify :
- Step 1: Prime factorize 85. The prime factors are 5 and 17.
- Step 2: Since there are no pairs of prime factors, cannot be simplified further.
Therefore, remains as since 85 has no perfect square factors other than 1.
Understanding this process is essential for simplifying more complex square roots and is a fundamental skill in algebra and higher mathematics.
Checking for Perfect Squares
To determine whether a number is a perfect square, we need to see if its square root is an integer. A perfect square is a number that can be expressed as the product of an integer with itself.
Here are the steps to check if 85 is a perfect square:
- Prime Factorization: First, perform prime factorization on the number. For 85, the prime factors are 5 and 17, as 85 = 5 × 17.
- Check the Exponents: In the prime factorization, if all prime factors have even exponents, the number is a perfect square. In the case of 85, both 5 and 17 have an exponent of 1, which are odd.
- Conclusion: Since the exponents of the prime factors are not all even, 85 is not a perfect square.
To further understand, here’s a simple example of a perfect square:
- The number 36 can be expressed as 6 × 6. Its prime factorization is 22 × 32. Since all exponents are even, 36 is a perfect square.
For any number that is not a perfect square, its square root will not be an integer and can only be expressed in decimal form or simplest radical form. For example, the square root of 85 is approximately 9.2195, which confirms that 85 is not a perfect square.
Step-by-Step Simplification of √85
Simplifying the square root of 85 involves several steps. While 85 is not a perfect square and cannot be simplified to an exact whole number, understanding the process is essential for dealing with other numbers that can be simplified.
- Prime Factorization:
First, find the prime factors of 85. A prime factor is a factor that is a prime number.
- 85 can be written as 85 = 5 × 17.
- Both 5 and 17 are prime numbers.
- Grouping Factors:
Next, group the factors in pairs of the same number. Since 85 is the product of two distinct prime numbers, it does not have any pairs of prime factors.
- Prime factors of 85: 51 and 171.
- Since there are no pairs, we cannot simplify the square root any further.
- Square Root Representation:
Therefore, the square root of 85 remains as it is in its simplest radical form:
\[\sqrt{85}\]
- Decimal Form:
For practical purposes, it is often useful to approximate the square root of 85 in decimal form:
\[\sqrt{85} \approx 9.2195\]
Thus, while √85 cannot be simplified into a smaller radical form, understanding the steps ensures that we can handle other numbers that might have perfect square factors.
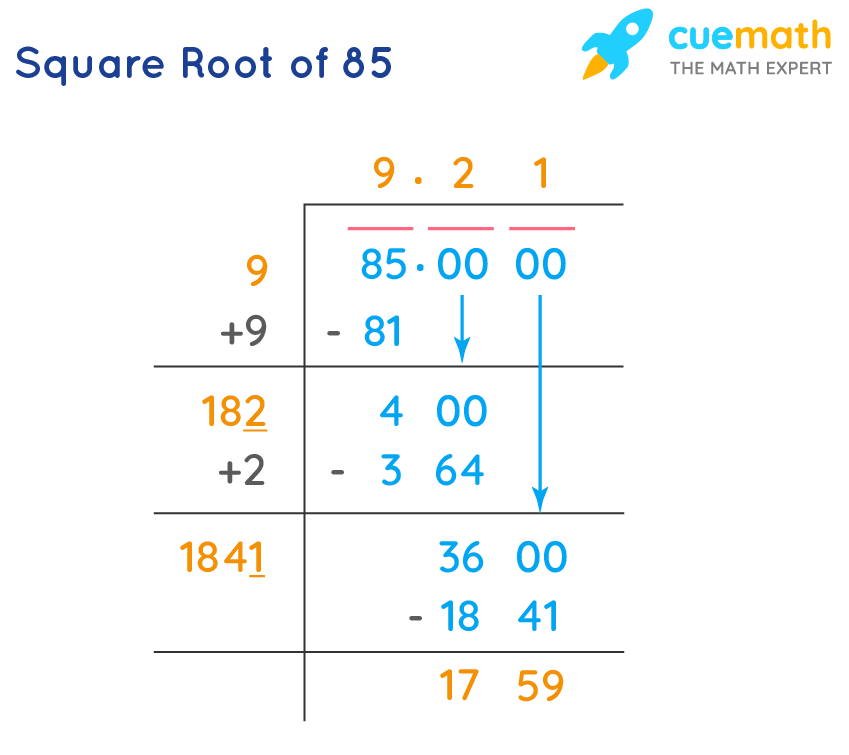
Approximate Value of √85
To find the approximate value of \(\sqrt{85}\), we need to use numerical methods or a calculator as the square root of 85 is an irrational number. Here is a step-by-step guide to approximate \(\sqrt{85}\):
-
Start with an initial guess. Since \(9^2 = 81\) and \(10^2 = 100\), we know that \(\sqrt{85}\) is between 9 and 10. Let's start with 9.
-
Divide 85 by the initial guess:
\[
\frac{85}{9} \approx 9.4444
\] -
Average the result with the initial guess:
\[
\frac{9 + 9.4444}{2} \approx 9.2222
\] -
Repeat the process with the new guess:
\[
\frac{85}{9.2222} \approx 9.2169
\]Average again:
\[
\frac{9.2222 + 9.2169}{2} \approx 9.2196
\] -
Continue this iterative process until the desired accuracy is achieved. After several iterations, you will find that:
\[
\sqrt{85} \approx 9.2195
\]
This method is known as the Babylonian method or Heron's method. It provides a good approximation through repeated averaging.
Alternatively, using a calculator, we find:
\[
\sqrt{85} \approx 9.2195444572929
\]
This value is rounded to 9.2195 for simplicity, but more decimal places can be kept for higher precision.
Knowing the approximate value of \(\sqrt{85}\) is useful in various applications, such as in geometry and physics, where precise measurements are often required.
Applications of Simplifying Square Roots
Simplifying square roots is not just an academic exercise; it has several practical applications in various fields. Here are some key areas where simplified square roots are utilized:
-
Geometry and Construction:
In geometry, the length of the sides of squares and right triangles often involves square roots. For example, the diagonal of a square with side length \( s \) is \( s\sqrt{2} \). Simplified square roots help in precise calculations of lengths and distances in construction projects.
Area (square units) Length of side (units) 9 \(\sqrt{9} = 3\) 144 \(\sqrt{144} = 12\) A \(\sqrt{A}\) -
Physics and Engineering:
Square roots are essential in formulas related to motion, energy, and waves. For example, in gravity calculations, the time \( t \) it takes for an object to fall from a height \( h \) is given by \( t = \frac{\sqrt{h}}{4} \). Simplified square roots allow engineers and physicists to solve such equations efficiently.
Example: If an object is dropped from a height of 64 feet:
\[
t = \frac{\sqrt{64}}{4} = \frac{8}{4} = 2 \text{ seconds}
\] -
Accident Investigation:
Police use square roots to determine the speed of a car before applying brakes based on the length of skid marks. The formula \( v = \sqrt{24d} \) (where \( v \) is the speed in mph and \( d \) is the skid mark length in feet) involves square roots.
Example: For skid marks measuring 190 feet:
\[
v = \sqrt{24 \times 190} \approx 67.5 \text{ mph}
\] -
Architecture:
Architects use square roots to determine distances and dimensions in designs, especially when dealing with right angles and diagonal measurements. This helps in creating accurate blueprints and ensuring the structural integrity of buildings.
-
Astronomy:
In astronomy, calculating distances between celestial bodies often involves square roots. Simplifying these roots makes it easier to understand and communicate vast distances in space.
Common Mistakes to Avoid
When simplifying square roots, several common mistakes can hinder your understanding and accuracy. Here are some key points to remember to avoid these errors:
-
Incorrect Factorization:
One of the most frequent mistakes is not correctly factoring the number under the square root. Ensure you factorize the number into its prime factors properly.
For example, for \(\sqrt{85}\), the prime factors are 5 and 17 (since \(85 = 5 \times 17\)).
-
Missing Perfect Squares:
Failing to identify perfect square factors is a common error. Always check if the number can be broken down into smaller parts that include perfect squares.
Example: Simplify \(\sqrt{18}\).
\[
\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}
\] -
Incorrect Application of Properties:
Ensure proper use of square root properties, such as \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\). Misapplication can lead to incorrect simplifications.
Example: Simplify \(\sqrt{12}\).
\[
\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}
\] -
Incorrect Simplification of Non-Simplifiable Roots:
Sometimes, a square root cannot be simplified further if there are no perfect square factors. Recognize when a square root is already in its simplest form.
Example: \(\sqrt{85}\) cannot be simplified further as its only factors are 1, 5, 17, and 85, none of which are perfect squares.
-
Forgetting to Simplify Completely:
Always simplify to the most reduced form. Partial simplification can leave expressions more complicated than necessary.
Example: Simplify \(\sqrt{50}\).
\[
\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}
\]
Practice Problems
Practicing the simplification of square roots helps solidify understanding and improves problem-solving skills. Below are several practice problems to test your ability to simplify square roots.
-
Simplify the following square roots:
- \(\sqrt{50}\)
- \(\sqrt{72}\)
- \(\sqrt{98}\)
- \(\sqrt{128}\)
-
Simplify and express the following square roots in terms of prime factors:
- \(\sqrt{75}\)
- \(\sqrt{45}\)
- \(\sqrt{200}\)
- \(\sqrt{180}\)
-
Combine and simplify the following expressions:
- \(\sqrt{12} \times \sqrt{3}\)
- \(\sqrt{8} + \sqrt{18}\)
- \(\frac{\sqrt{50}}{\sqrt{2}}\)
- \(\sqrt{20} \cdot \sqrt{5} - \sqrt{100}\)
-
Solve the following equations involving square roots:
- \(\sqrt{x + 5} = 4\)
- \(\sqrt{3x - 1} = 7\)
- \(2\sqrt{2x + 3} = 10\)
- \(\sqrt{5x + 20} = \sqrt{3x + 12}\)
-
Simplify the following complex expressions:
- \(\sqrt{75} + 3\sqrt{3} - \sqrt{12}\)
- \(2\sqrt{18} - \sqrt{8} + \sqrt{50}\)
- \(\sqrt{45} + \sqrt{20} - \sqrt{5}\)
- \(\sqrt{32} \cdot \sqrt{2} + \sqrt{128}\)
Remember to factorize the numbers under the square roots and simplify them step by step. Practicing these problems will help you become more comfortable with the process of simplifying square roots and applying the properties of radicals.

Conclusion
In conclusion, simplifying the square root of 85 involves understanding that it cannot be simplified into a simpler radical form. This is because 85 is not a perfect square and its prime factors, 5 and 17, do not pair up to form a perfect square. Thus, the square root of 85 remains in its simplest radical form as √85.
However, for practical purposes, we often use the decimal approximation, which is approximately 9.21954. This value is useful in various applications such as geometry, engineering, and daily life calculations where precise measurements are required.
Understanding the properties of square roots and the process of simplification is crucial for solving complex mathematical problems efficiently. Here are the key takeaways:
- The square root of 85 in simplest radical form is √85.
- The decimal approximation of √85 is 9.21954.
- 85 is not a perfect square because its prime factors do not form pairs.
By mastering these concepts, you can confidently approach problems involving square roots, whether in academic settings or real-world scenarios. Remember, the ability to simplify square roots enhances your problem-solving skills and mathematical understanding.
We encourage you to practice with more examples and explore the fascinating world of mathematics further. Simplifying square roots is just one of many topics that reveal the beauty and utility of math in our daily lives.
Video này hướng dẫn cách đơn giản hóa căn bậc hai của 85, giúp bạn nắm vững kiến thức toán học một cách dễ dàng và hiệu quả.
Căn Bậc Hai của 85
READ MORE:
Video này hướng dẫn cách đơn giản hóa căn bậc hai của một số không phải là số chính phương, giúp bạn hiểu rõ hơn về khái niệm này trong toán học.
Cách Đơn Giản Hóa Căn Bậc Hai của Một Số Không Phải Là Số Chính Phương
















