Topic square root 54 simplified: Simplifying the square root of 54 can seem daunting, but it's easier than you might think! This guide will walk you through the steps to break down and simplify √54, making complex math a breeze. Whether you're a student or just curious, you'll find clear and concise instructions to help you master this concept.
Table of Content
- Square Root of 54 Simplified
- Introduction to Square Roots
- Understanding Simplification
- Prime Factorization Method
- Steps to Simplify √54
- Breaking Down the Factors
- Combining Like Terms
- Final Simplified Form
- Practical Applications of √54
- Additional Practice Problems
- Common Mistakes to Avoid
- FAQs on Simplifying Square Roots
- Conclusion
- YOUTUBE:
Square Root of 54 Simplified
The square root of 54 simplified is:
\[
\sqrt{54} = \sqrt{2 \times 27} = \sqrt{2 \times 3^3} = 3\sqrt{6}
\]
READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is a fundamental concept in mathematics that helps in solving various equations and understanding geometric properties. The square root is represented by the radical symbol (√).
For example, the square root of 25 is 5 because \(5 \times 5 = 25\). In mathematical notation, this is written as \( \sqrt{25} = 5 \).
Understanding square roots involves recognizing both perfect squares and non-perfect squares:
- Perfect Squares: These are numbers whose square roots are whole numbers. Examples include 1, 4, 9, 16, 25, etc.
- Non-Perfect Squares: These numbers do not have whole numbers as their square roots. Examples include 2, 3, 5, 7, 8, etc.
When dealing with non-perfect squares, the square root is often simplified to make calculations easier. This simplification process involves finding the prime factors of the number.
Let's look at an example to illustrate the simplification of a square root. We'll use the square root of 54:
- Find the Prime Factors: Break down 54 into its prime factors: \(54 = 2 \times 3 \times 3 \times 3\).
- Group the Factors: Pair the factors: \(54 = 2 \times (3 \times 3) \times 3 = 2 \times 9 \times 3\).
- Simplify the Expression: Take the square root of the perfect square (9): \( \sqrt{54} = \sqrt{2 \times 9 \times 3} = \sqrt{2} \times \sqrt{9} \times \sqrt{3} = \sqrt{2} \times 3 \times \sqrt{3} = 3\sqrt{6} \).
Thus, the simplified form of the square root of 54 is \( 3\sqrt{6} \).
Understanding Simplification
Simplifying square roots involves reducing a square root to its simplest form. This process helps in making calculations easier and results more understandable. To simplify the square root of a number, you break it down into its prime factors and then apply the properties of square roots to combine like terms.
Here is a step-by-step approach to understanding simplification:
- Identify the prime factors of the number under the square root.
- Group the prime factors into pairs of identical numbers.
- Move each pair of identical numbers out from under the square root, simplifying them to a single number.
- Multiply the numbers outside the square root together and keep any remaining factors inside the square root.
Let's illustrate this process with the square root of 54.
- Prime factorization of 54: \( 54 = 2 \times 3 \times 3 \times 3 \)
- Pair the identical factors: \( 54 = 2 \times 3^2 \times 3 \)
- Extract the pairs: \( \sqrt{54} = \sqrt{2 \times 3^2 \times 3} = 3\sqrt{6} \)
Therefore, the simplified form of \( \sqrt{54} \) is \( 3\sqrt{6} \).
This method can be applied to any square root, making it a versatile and essential tool in mathematics.
Prime Factorization Method
The prime factorization method is a systematic approach to simplifying square roots by breaking down a number into its prime factors. This method ensures that the square root is expressed in its simplest form. Here are the detailed steps to use the prime factorization method to simplify the square root of 54:
- Find the prime factors of 54:
- Start by dividing 54 by the smallest prime number, which is 2. Since 54 is even, it is divisible by 2.
- \( 54 \div 2 = 27 \)
- Next, find the prime factors of 27. Since 27 is odd, it is not divisible by 2. Try the next smallest prime number, which is 3.
- \( 27 \div 3 = 9 \)
- Continue factoring 9 by dividing by 3 again.
- \( 9 \div 3 = 3 \)
- Finally, divide 3 by 3.
- \( 3 \div 3 = 1 \)
Thus, the prime factors of 54 are \( 2 \times 3 \times 3 \times 3 \) or \( 2 \times 3^3 \).
- Group the prime factors into pairs:
Pair the identical factors to simplify the square root.
- The prime factors of 54 can be grouped as \( 2 \times (3 \times 3) \times 3 \).
- Write this as \( 2 \times 3^2 \times 3 \).
- Simplify by taking out the pairs:
- For every pair of identical factors, one factor comes out of the square root.
- \( \sqrt{54} = \sqrt{2 \times 3^2 \times 3} \)
- Since \( 3^2 \) is a perfect square, it simplifies to 3 outside the square root.
- \( \sqrt{54} = 3 \sqrt{2 \times 3} = 3 \sqrt{6} \)
Therefore, using the prime factorization method, the square root of 54 simplifies to \( 3\sqrt{6} \). This method helps in clearly understanding the process of breaking down and simplifying square roots.
Steps to Simplify √54
Simplifying the square root of 54 involves breaking down the number into its prime factors and then simplifying the expression step by step. Below is a detailed, step-by-step guide to simplify \( \sqrt{54} \).
- Find the Prime Factors:
First, we need to find the prime factors of 54. The prime factorization of 54 is:
- 54 is divisible by 2 (the smallest prime number): \( 54 \div 2 = 27 \).
- 27 is divisible by 3: \( 27 \div 3 = 9 \).
- 9 is divisible by 3: \( 9 \div 3 = 3 \).
- 3 is a prime number: \( 3 \div 3 = 1 \).
So, the prime factorization of 54 is \( 2 \times 3 \times 3 \times 3 \) or \( 2 \times 3^3 \).
- Group the Factors:
Next, group the prime factors into pairs:
- \( 2 \times 3 \times 3 \times 3 = 2 \times (3 \times 3) \times 3 \).
- Write this as \( 2 \times 3^2 \times 3 \).
- Simplify the Square Root:
Apply the property of square roots that allows us to take out pairs of identical factors:
- \( \sqrt{54} = \sqrt{2 \times 3^2 \times 3} \).
- Since \( 3^2 \) is a perfect square, it can be simplified to 3 outside the square root:
- \( \sqrt{54} = \sqrt{2 \times 9 \times 3} = \sqrt{2 \times 3^2 \times 3} = 3 \sqrt{2 \times 3} \).
- Therefore, \( \sqrt{54} = 3 \sqrt{6} \).
Thus, the square root of 54 simplified is \( 3\sqrt{6} \). This process of simplification helps in reducing complex expressions into simpler, more manageable forms.

Breaking Down the Factors
To simplify \( \sqrt{54} \), we need to break down the number into its prime factors. This process involves dividing the number by the smallest possible prime numbers until we reach 1. Here's a detailed step-by-step breakdown:
- Start with the Number:
We begin with the number 54.
- Divide by the Smallest Prime Number:
The smallest prime number is 2. Since 54 is even, it is divisible by 2.
- \( 54 \div 2 = 27 \)
- Continue with the Next Prime Number:
Next, we need to factor 27. The smallest prime number that divides 27 is 3.
- \( 27 \div 3 = 9 \)
- Factor Further:
We continue factoring 9. It is also divisible by 3.
- \( 9 \div 3 = 3 \)
- Factor the Remaining Prime Number:
Finally, 3 is a prime number.
- \( 3 \div 3 = 1 \)
After breaking down 54, we find the prime factors:
- 54 = \( 2 \times 3 \times 3 \times 3 \)
- This can also be written as \( 2 \times 3^3 \).
By breaking down the factors in this way, we can see clearly how to proceed with simplifying the square root. Each pair of identical factors can be taken out of the square root, which simplifies the expression.
Combining Like Terms
Once we have broken down the number 54 into its prime factors, the next step in simplifying \( \sqrt{54} \) is to combine like terms. This involves grouping the prime factors in pairs and simplifying the square root expression. Here is a detailed step-by-step guide:
- Prime Factorization:
We start with the prime factorization of 54:
- 54 = \( 2 \times 3 \times 3 \times 3 \)
- This can be written as \( 2 \times 3^3 \).
- Group the Like Terms:
Next, group the identical factors into pairs:
- \( 2 \times 3 \times 3 \times 3 = 2 \times (3 \times 3) \times 3 \)
- Or, \( 2 \times 3^2 \times 3 \).
- Simplify the Pairs:
For every pair of identical factors, one factor can be taken out of the square root:
- \( \sqrt{54} = \sqrt{2 \times 3^2 \times 3} \)
- \( \sqrt{54} = \sqrt{2 \times 9 \times 3} \)
- \( \sqrt{54} = \sqrt{18 \times 3} \)
- Combine Like Terms Outside the Square Root:
Take the square root of the perfect squares and move them outside the square root:
- Since \( 3^2 = 9 \), \( \sqrt{9} = 3 \), we can simplify:
- \( \sqrt{54} = 3 \sqrt{6} \)
Therefore, by combining like terms, the simplified form of \( \sqrt{54} \) is \( 3\sqrt{6} \). This process helps in reducing the complexity of the square root expression, making it easier to work with.
Final Simplified Form
After breaking down the factors and combining like terms, the final step is to express the square root of 54 in its simplest form. Here is a detailed, step-by-step process to arrive at the final simplified form:
- Start with Prime Factorization:
The prime factorization of 54 is:
- 54 = \( 2 \times 3 \times 3 \times 3 \)
- This can be written as \( 2 \times 3^3 \).
- Group the Factors:
Group the identical factors into pairs:
- \( 2 \times 3 \times 3 \times 3 = 2 \times (3 \times 3) \times 3 \)
- Or, \( 2 \times 3^2 \times 3 \).
- Simplify by Taking Out Pairs:
For every pair of identical factors, take one factor out of the square root:
- \( \sqrt{54} = \sqrt{2 \times 3^2 \times 3} \)
- \( \sqrt{54} = \sqrt{2 \times 9 \times 3} \)
- Extract the Perfect Squares:
The square root of \( 9 \) (which is \( 3^2 \)) can be simplified to 3:
- \( \sqrt{54} = \sqrt{9 \times 6} \)
- \( \sqrt{54} = 3 \sqrt{6} \)
Therefore, the final simplified form of \( \sqrt{54} \) is:
\( 3\sqrt{6} \)
This final simplified form makes it easier to handle the square root in various mathematical applications and provides a clear, concise representation of the original number.
Practical Applications of √54
The square root of 54, simplified as \( 3\sqrt{6} \), has various practical applications in different fields. Understanding these applications helps in appreciating the importance of simplifying square roots. Here are some detailed practical applications:
- Geometry and Trigonometry:
In geometry, the square root of 54 can be used in calculating the length of the sides of triangles, especially in right-angled triangles where the Pythagorean theorem is applied. For example, if the length of the hypotenuse is \( \sqrt{54} \) units, it simplifies to \( 3\sqrt{6} \) units, making calculations easier.
- Physics and Engineering:
In physics, square roots often appear in formulas related to motion, energy, and waves. For instance, in calculating the natural frequency of a system, the square root of various quantities is used. Knowing \( \sqrt{54} = 3\sqrt{6} \) allows for quicker simplification in complex equations.
- Statistics and Probability:
In statistics, standard deviation and variance calculations involve square roots. If a data set has a variance of 54, the standard deviation is \( \sqrt{54} = 3\sqrt{6} \). This simplification is useful for interpreting data more efficiently.
- Computer Science:
Algorithms in computer science often require the use of square roots, particularly in graphics and simulations. Simplifying \( \sqrt{54} \) to \( 3\sqrt{6} \) can optimize performance by reducing the complexity of computations.
- Real-World Measurements:
In real-world scenarios, such as construction and design, precise measurements are crucial. If a dimension involves \( \sqrt{54} \), simplifying it to \( 3\sqrt{6} \) aids in accurate material calculations and cost estimations.
Understanding the practical applications of \( \sqrt{54} \) demonstrates the importance of mathematical simplification in various disciplines, enhancing both theoretical knowledge and practical skills.
Additional Practice Problems
Here are some additional practice problems to help you master the simplification of square roots:
- √32
- √72
- √98
- √200
- √128
- √18
- √50
- √242
- √288
- √320
To simplify these square roots, follow these steps:
- Find the prime factorization of the number inside the square root.
- Group the prime factors into pairs.
- Move each pair of prime factors outside the square root.
- Multiply the numbers outside the square root.
- Simplify the expression inside the square root if possible.
Let's work through the first problem as an example:
Simplifying √32:
- Prime factorization of 32: 32 = 2 × 2 × 2 × 2 × 2
- Group the prime factors into pairs: (2 × 2) × (2 × 2) × 2
- Move each pair of prime factors outside the square root: 2 × 2 × √2
- Multiply the numbers outside the square root: 4√2
- Final simplified form: √32 = 4√2
Now, try simplifying the other square roots following the same steps. Here are the prime factorizations to get you started:
| Square Root | Prime Factorization |
|---|---|
| √72 | 72 = 2 × 2 × 2 × 3 × 3 |
| √98 | 98 = 2 × 7 × 7 |
| √200 | 200 = 2 × 2 × 2 × 5 × 5 |
| √128 | 128 = 2 × 2 × 2 × 2 × 2 × 2 × 2 |
| √18 | 18 = 2 × 3 × 3 |
| √50 | 50 = 2 × 5 × 5 |
| √242 | 242 = 2 × 11 × 11 |
| √288 | 288 = 2 × 2 × 2 × 2 × 2 × 3 × 3 |
| √320 | 320 = 2 × 2 × 2 × 2 × 2 × 2 × 5 |
Practice these problems to gain confidence in simplifying square roots!
Common Mistakes to Avoid
Simplifying square roots can be tricky, and there are some common mistakes students often make when simplifying the square root of 54. Here are some of the most frequent errors and how to avoid them:
-
Incorrect Prime Factorization:
Ensure you correctly factorize the number under the square root. For 54, the prime factorization is 54 = 2 × 3 × 3 × 3. An incorrect factorization will lead to an incorrect simplification.
-
Forgetting to Simplify Completely:
After factorizing, make sure to simplify the square root completely. For √54, you should recognize that 54 = 3² × 6, which simplifies to 3√6. Stopping at √(9 × 6) without further simplification is a common mistake.
-
Misinterpreting the Radical Form:
Students often leave the answer in an incomplete form such as √54 instead of the simplest form 3√6. Always ensure you simplify to the fullest extent.
-
Incorrect Handling of Negative Roots:
Confusing real and imaginary roots is another mistake. Remember, √54 has real roots, whereas √-54 involves imaginary numbers. Do not mix these up.
-
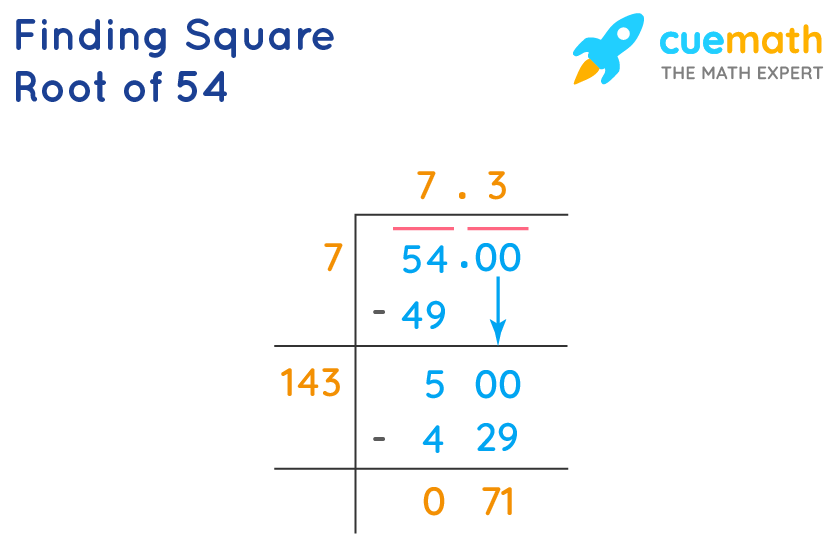
Decimal Approximation Errors:
When approximating the square root to a decimal, ensure accuracy. The square root of 54 is approximately 7.348, but using too many or too few decimal places can lead to inaccuracies, especially in higher-level calculations.
By avoiding these common mistakes, you can ensure accurate and simplified solutions for square roots like √54.
FAQs on Simplifying Square Roots
- What is the square root of 54?
The square root of 54 is approximately 7.348 when rounded to three decimal places.
- How do you simplify the square root of 54?
The simplest form of the square root of 54 is \(3\sqrt{6}\). This is derived by factoring 54 into its prime factors \(54 = 2 \times 3^3\) and then simplifying under the radical sign.
- Why is \(\sqrt{54}\) an irrational number?
The square root of 54 is irrational because it cannot be expressed as a fraction of two integers. Its decimal form is non-terminating and non-repeating.
- What are the steps to simplify \(\sqrt{54}\)?
- Factor 54 into its prime factors: \(54 = 2 \times 3^3\).
- Rewrite under the square root: \(\sqrt{54} = \sqrt{2 \times 3^3}\).
- Group the factors in pairs: \(\sqrt{54} = \sqrt{3^2 \times 6}\).
- Take the square root of the perfect square: \(\sqrt{54} = 3\sqrt{6}\).
- Can the square root of 54 be simplified further?
No, \(3\sqrt{6}\) is the simplest radical form of the square root of 54.
- Is \(\sqrt{54}\) a rational number?
No, \(\sqrt{54}\) is an irrational number.
- What is the square root of 54 in decimal form?
The decimal form of the square root of 54 is approximately 7.3484692283495.
Conclusion
Simplifying the square root of 54 may seem challenging at first, but by following systematic steps, it becomes quite manageable. The key steps include breaking down the number into its prime factors, identifying and extracting the perfect square factors, and then simplifying the expression. In the case of √54, we factorize it as 54 = 2 × 32 × 3, which allows us to simplify it to 3√6.
Understanding and mastering these steps can help in simplifying not just √54 but any other square root as well. Simplifying square roots is a valuable skill in algebra and beyond, aiding in solving equations and understanding numerical relationships.
In addition, being aware of common mistakes and practicing regularly with various problems will enhance your proficiency. Whether for academic purposes or practical applications, such as measurements and calculations, having a solid grasp of square root simplification is beneficial.
As you continue to practice, you'll find that these processes become more intuitive, making it easier to handle more complex mathematical problems. Remember, every mathematical concept is a building block for more advanced topics, and mastering the basics of square root simplification is a significant step in your mathematical journey.
We hope this guide has provided you with a clear understanding and practical approach to simplifying square roots. Keep practicing, and don't hesitate to revisit the foundational steps whenever needed. Happy calculating!

Cách Đơn Giản Hóa Căn Bậc Hai Của 54: Sqrt(54)
READ MORE:
Đơn Giản Hóa Căn Bậc Hai Của 54

















