Topic how to simplify the square root of 72: Discover the easy and effective method to simplify the square root of 72 with our comprehensive guide. This step-by-step approach will help you break down the process, making it simple to understand and apply. Perfect for students and math enthusiasts looking to master simplifying square roots!
Table of Content
- How to Simplify the Square Root of 72
- Introduction
- Understanding Square Roots
- What Does it Mean to Simplify a Square Root?
- Prime Factorization
- Steps to Simplify the Square Root of 72
- Breaking Down 72 into Prime Factors
- Grouping Factors into Pairs
- Extracting Pairs from the Square Root
- Final Simplification
- Practice Problems
- Common Mistakes to Avoid
- Tips for Simplifying Square Roots
- Applications of Simplified Square Roots
- YOUTUBE: Video hướng dẫn cách tốt nhất để đơn giản hóa căn bậc hai của một số, cụ thể là căn bậc hai của 72. Hãy theo dõi để hiểu rõ hơn và áp dụng vào các bài toán thực tế.
How to Simplify the Square Root of 72
Simplifying the square root of 72 involves finding the prime factors of 72 and then simplifying the expression by grouping the factors into pairs. Here is a detailed step-by-step guide:
Step-by-Step Process
-
First, find the prime factorization of 72:
- 72 can be divided by 2: \(72 \div 2 = 36\)
- 36 can be divided by 2: \(36 \div 2 = 18\)
- 18 can be divided by 2: \(18 \div 2 = 9\)
- 9 can be divided by 3: \(9 \div 3 = 3\)
- 3 can be divided by 3: \(3 \div 3 = 1\)
So, the prime factorization of 72 is \(72 = 2^3 \times 3^2\).
-
Next, express the square root of 72 in terms of its prime factors:
\(\sqrt{72} = \sqrt{2^3 \times 3^2}\)
-
Group the factors into pairs:
\(\sqrt{2^3 \times 3^2} = \sqrt{(2^2 \times 2) \times (3^2)}\)
-
Simplify the square root by taking out pairs of factors as single numbers:
\(\sqrt{(2^2 \times 2) \times (3^2)} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{2}\)
\(\sqrt{2^2} = 2\) and \(\sqrt{3^2} = 3\), so:
\(\sqrt{72} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\)
Conclusion
The simplified form of the square root of 72 is \(6\sqrt{2}\).

READ MORE:
Introduction
Simplifying the square root of 72 is a fundamental skill in algebra that involves breaking down the number into its prime factors and simplifying the expression by pairing the factors. This process makes it easier to work with the square root in equations and other mathematical problems. In this guide, we will walk you through the step-by-step process of simplifying \(\sqrt{72}\).
Here's a quick overview of what we'll cover:
- Understanding square roots and their properties.
- Finding the prime factorization of 72.
- Grouping the factors into pairs.
- Extracting the pairs from under the square root.
- Writing the simplified form of \(\sqrt{72}\).
By the end of this guide, you will be able to simplify the square root of 72 with confidence and apply this technique to other square roots as well. Let's get started!
Understanding Square Roots
Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the original number. The square root of a number \( n \) is denoted as \(\sqrt{n}\). For example, the square root of 9 is 3 because \( 3 \times 3 = 9 \).
There are some key properties of square roots that are useful to understand:
- Non-negative results: The square root of a positive number is always non-negative. For instance, \(\sqrt{16} = 4\), not -4, even though \((-4) \times (-4) = 16\).
- Product Property: The square root of a product is the product of the square roots of the factors. Mathematically, \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\). This property is crucial in simplifying square roots.
- Quotient Property: The square root of a quotient is the quotient of the square roots of the numerator and denominator: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
- Perfect Squares: Numbers like 1, 4, 9, 16, 25, and so on are perfect squares because their square roots are whole numbers.
In algebra, simplifying square roots often involves finding the prime factorization of the number under the square root. This means breaking the number down into its prime factors and then using the product property to simplify.
For example, to simplify \(\sqrt{72}\), we start by finding the prime factors of 72. Prime factorization helps us rewrite 72 as a product of prime numbers, which can then be grouped to simplify the square root. This method can be applied to any square root to make it easier to work with in equations and other mathematical contexts.
Next, we'll delve into the specific steps to simplify the square root of 72.
What Does it Mean to Simplify a Square Root?
Simplifying a square root means expressing it in its simplest form, where the number inside the square root (the radicand) has no perfect square factors other than 1. This process makes the square root easier to understand and work with in mathematical equations.
Here are the steps to simplify a square root:
-
Find the prime factorization of the radicand:
Break down the number under the square root into its prime factors. For example, the prime factorization of 72 is \(2^3 \times 3^2\).
-
Group the factors into pairs:
Pair the prime factors in the factorization. Each pair of the same number can be simplified because the square root of a square is the number itself. For 72, the factor pairs are \(2^2 \times 2 \times 3^2\).
-
Simplify by taking out pairs:
For each pair of factors, take one factor out of the square root. In this case, \(\sqrt{2^2 \times 3^2 \times 2} = 2 \times 3 \times \sqrt{2}\).
-
Write the simplified form:
Combine the factors outside the square root. For 72, the simplified form is \(6\sqrt{2}\).
By following these steps, we ensure that the square root is expressed in its simplest form, making it easier to work with in further mathematical calculations. This method can be applied to any number to simplify its square root effectively.
Prime Factorization
Prime factorization is the process of breaking down a composite number into its prime factors. Prime factors are the prime numbers that multiply together to give the original number. This is a crucial step in simplifying square roots.
To find the prime factorization of 72, follow these steps:
-
Divide by the smallest prime number:
Start by dividing 72 by the smallest prime number, which is 2. Since 72 is even, it is divisible by 2.
\(72 \div 2 = 36\)
-
Continue dividing by 2:
Keep dividing by 2 until you can no longer divide evenly.
\(36 \div 2 = 18\)
\(18 \div 2 = 9\)
-
Move to the next smallest prime number:
Now that 9 is not divisible by 2, move to the next smallest prime number, which is 3.
\(9 \div 3 = 3\)
\(3 \div 3 = 1\)
-
List the prime factors:
Once you reach 1, list all the prime numbers you used to divide. The prime factorization of 72 is:
\(72 = 2 \times 2 \times 2 \times 3 \times 3\)
Or, in exponential form:
\(72 = 2^3 \times 3^2\)
Understanding the prime factorization of a number is essential for simplifying square roots. In the next section, we will use these prime factors to simplify the square root of 72.

Steps to Simplify the Square Root of 72
Simplifying the square root of 72 involves breaking it down into its prime factors and then simplifying the expression by grouping the factors. Here are the detailed steps:
-
Find the prime factorization of 72:
First, determine the prime factors of 72. The prime factorization of 72 is:
\(72 = 2 \times 2 \times 2 \times 3 \times 3\)
Or, in exponential form:
\(72 = 2^3 \times 3^2\)
-
Rewrite the square root using prime factors:
Express the square root of 72 using its prime factors:
\(\sqrt{72} = \sqrt{2^3 \times 3^2}\)
-
Group the factors into pairs:
Group the prime factors in pairs, as each pair of identical factors can be taken out of the square root:
\(\sqrt{2^3 \times 3^2} = \sqrt{(2^2 \times 2) \times (3^2)}\)
-
Simplify by taking out pairs:
For each pair of identical factors, take one factor out of the square root:
\(\sqrt{(2^2 \times 2) \times (3^2)} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{2}\)
\(\sqrt{2^2} = 2\) and \(\sqrt{3^2} = 3\), so the expression simplifies to:
\(2 \times 3 \times \sqrt{2}\)
-
Write the simplified form:
Combine the factors outside the square root to get the final simplified form:
\(\sqrt{72} = 6\sqrt{2}\)
By following these steps, we can simplify the square root of 72 to \(6\sqrt{2}\), making it easier to work with in various mathematical contexts.
Breaking Down 72 into Prime Factors
To simplify the square root of 72, we first need to break down 72 into its prime factors. This process involves dividing 72 by the smallest prime numbers until we reach 1. Here is a step-by-step guide:
-
Start with the smallest prime number:
The smallest prime number is 2. Since 72 is even, it is divisible by 2.
\(72 \div 2 = 36\)
-
Continue dividing by 2:
Keep dividing by 2 as long as the quotient is even.
\(36 \div 2 = 18\)
\(18 \div 2 = 9\)
-
Move to the next smallest prime number:
Once the quotient is no longer even, move to the next smallest prime number, which is 3.
\(9 \div 3 = 3\)
\(3 \div 3 = 1\)
-
List all the prime factors:
The prime factorization of 72 can be written by listing all the prime numbers used to divide it.
\(72 = 2 \times 2 \times 2 \times 3 \times 3\)
Or, in exponential form:
\(72 = 2^3 \times 3^2\)
By breaking down 72 into its prime factors, we can see that it is composed of three 2's and two 3's. This prime factorization is essential for simplifying the square root of 72 in subsequent steps.
Grouping Factors into Pairs
To simplify the square root of 72, we need to group its prime factors into pairs. Let's break it down step by step:
-
First, find the prime factorization of 72. The prime factors of 72 are 2, 2, 2, 3, and 3.
\[
72 = 2 \times 2 \times 2 \times 3 \times 3
\] -
Next, group the factors into pairs. Grouping the factors of 72, we get:
- \(2 \times 2\)
- \(3 \times 3\)
- 2 (remaining factor)
\[
72 = (2 \times 2) \times (3 \times 3) \times 2
\] -
Now, we can simplify the expression by taking the square root of each pair of factors:
- \(\sqrt{2 \times 2} = 2\)
- \(\sqrt{3 \times 3} = 3\)
The remaining factor 2 stays under the square root:
\[
\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2}
\]
Therefore, the simplified form of the square root of 72 is:
\[
\sqrt{72} = 6\sqrt{2}
\]
Extracting Pairs from the Square Root
After grouping the prime factors of 72, the next step is to extract pairs from under the square root. Here's how to do it step by step:
-
Recall the prime factorization of 72 and how we grouped them into pairs:
- \((2 \times 2)\)
- \((3 \times 3)\)
- 2 (remaining factor)
\[
72 = (2 \times 2) \times (3 \times 3) \times 2
\] -
Take the square root of each pair of prime factors:
- \(\sqrt{2 \times 2} = 2\)
- \(\sqrt{3 \times 3} = 3\)
These pairs are now extracted from under the square root.
-
Combine the results with the remaining factor under the square root:
\[
\sqrt{72} = \sqrt{(2 \times 2) \times (3 \times 3) \times 2} = 2 \times 3 \times \sqrt{2}
\] -
Multiply the extracted factors together:
\[
2 \times 3 = 6
\]
Thus, the simplified form of the square root of 72 is:
\[
\sqrt{72} = 6\sqrt{2}
\]

Final Simplification
In this section, we will finalize the simplification of the square root of 72. We have already broken down the number into its prime factors and grouped them into pairs. Now, we will extract these pairs and simplify the expression to its simplest radical form.
- Recall that the prime factorization of 72 is:
\( 72 = 2^3 \times 3^2 \) - Group the prime factors into pairs of equal numbers:
\( 72 = (2^2) \times (3^2) \times 2 \) - Take the square root of each pair of prime factors:
\( \sqrt{72} = \sqrt{(2^2) \times (3^2) \times 2} \)
\( \sqrt{72} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{2} \) - Since the square root of a squared number is the number itself:
\( \sqrt{2^2} = 2 \) and \( \sqrt{3^2} = 3 \)
\( \sqrt{72} = 2 \times 3 \times \sqrt{2} \) - Multiply the numbers outside the radical sign:
\( \sqrt{72} = 6\sqrt{2} \)
Therefore, the simplified form of \( \sqrt{72} \) is \( 6\sqrt{2} \). This represents the most reduced form of the square root, where all perfect squares have been extracted and simplified.
Practice Problems
Practice problems are essential to mastering the process of simplifying square roots. Here are some practice problems with detailed steps to help you understand the simplification process better:
-
Problem 1: Simplify \( \sqrt{18} \)
- Prime factorize 18: \( 18 = 2 \times 3 \times 3 \)
- Group the factors into pairs: \( (3 \times 3) \times 2 \)
- Extract the pairs from the square root: \( \sqrt{3^2 \times 2} = 3\sqrt{2} \)
Solution: \( \sqrt{18} = 3\sqrt{2} \)
-
Problem 2: Simplify \( \sqrt{50} \)
- Prime factorize 50: \( 50 = 2 \times 5 \times 5 \)
- Group the factors into pairs: \( (5 \times 5) \times 2 \)
- Extract the pairs from the square root: \( \sqrt{5^2 \times 2} = 5\sqrt{2} \)
Solution: \( \sqrt{50} = 5\sqrt{2} \)
-
Problem 3: Simplify \( \sqrt{98} \)
- Prime factorize 98: \( 98 = 2 \times 7 \times 7 \)
- Group the factors into pairs: \( (7 \times 7) \times 2 \)
- Extract the pairs from the square root: \( \sqrt{7^2 \times 2} = 7\sqrt{2} \)
Solution: \( \sqrt{98} = 7\sqrt{2} \)
-
Problem 4: Simplify \( \sqrt{128} \)
- Prime factorize 128: \( 128 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \)
- Group the factors into pairs: \( (2 \times 2) \times (2 \times 2) \times (2 \times 2) \times 2 \)
- Extract the pairs from the square root: \( \sqrt{2^6 \times 2} = 2^3\sqrt{2} = 8\sqrt{2} \)
Solution: \( \sqrt{128} = 8\sqrt{2} \)
-
Problem 5: Simplify \( \sqrt{200} \)
- Prime factorize 200: \( 200 = 2 \times 2 \times 2 \times 5 \times 5 \)
- Group the factors into pairs: \( (2 \times 2) \times (5 \times 5) \times 2 \)
- Extract the pairs from the square root: \( \sqrt{2^2 \times 5^2 \times 2} = 2 \times 5 \sqrt{2} = 10\sqrt{2} \)
Solution: \( \sqrt{200} = 10\sqrt{2} \)
These practice problems will help you get comfortable with the steps involved in simplifying square roots. Make sure to factorize the number correctly, group the pairs, and extract them accurately to simplify the expression.
Common Mistakes to Avoid
When simplifying the square root of 72, certain mistakes are commonly made. Being aware of these pitfalls can help ensure accurate and efficient simplification:
- Overlooking Prime Factorization: Ensure you fully break down 72 into its prime factors. The correct factorization is \(72 = 2 \times 2 \times 2 \times 3 \times 3\). Missing a factor can lead to incorrect simplification.
- Incorrect Grouping of Factors: Each pair of identical factors should be used to simplify the root. In this case, \(2 \times 2\) and \(3 \times 3\) form the pairs. Failure to correctly pair these factors will result in errors.
- Misplacing Factors Outside the Square Root: After identifying pairs, each pair should contribute one factor outside the square root. For \( \sqrt{72} \), both \(2 \times 2\) and \(3 \times 3\) should result in \(2 \times 3 = 6\) outside the square root.
- Ignoring Leftover Factors: Any unpaired factors must remain under the square root. For \( \sqrt{72} \), the leftover factor is \(2\), resulting in the simplified form \(6\sqrt{2}\).
- Mathematical Errors in Simplification: Simple arithmetic mistakes can occur during calculations. Always double-check your work for accuracy to ensure correct results.
By avoiding these common mistakes, you can simplify the square root of 72 accurately and efficiently.
Tips for Simplifying Square Roots
Simplifying square roots can be made easier with a few helpful tips and strategies. Here are some tips to help you simplify square roots effectively:
- Understand Prime Factorization: Breaking down a number into its prime factors is essential. For example, for 72, the prime factorization is \( 72 = 2^3 \times 3^2 \).
- Identify Pairs of Factors: Group the prime factors into pairs to simplify the square root. Each pair of identical factors can be taken out of the square root. For example, for \( \sqrt{72} \):
- Prime factorization of 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Grouping into pairs: \( (2 \times 2) \) and \( (3 \times 3) \).
- Extract Pairs from the Square Root: Each pair of factors comes out of the square root as a single factor. Using the example above:
\[ \sqrt{72} = \sqrt{2 \times 2 \times 2 \times 3 \times 3} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \]
- Practice with Different Numbers: Practice simplifying square roots of various numbers to get comfortable with the process. For instance, simplify \( \sqrt{50} \):
- Prime factorization: \( 50 = 2 \times 5 \times 5 \).
- Grouping into pairs: \( 5 \times 5 \).
- Extracting pairs: \[ \sqrt{50} = \sqrt{2 \times 5 \times 5} = 5\sqrt{2} \]
- Utilize the Property of Square Roots: Remember that \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). This property can simplify the process significantly.
- Practice Regularly: The more you practice, the more familiar you will become with common square roots and the simplification process.
By following these tips, you can simplify square roots more easily and with greater confidence.
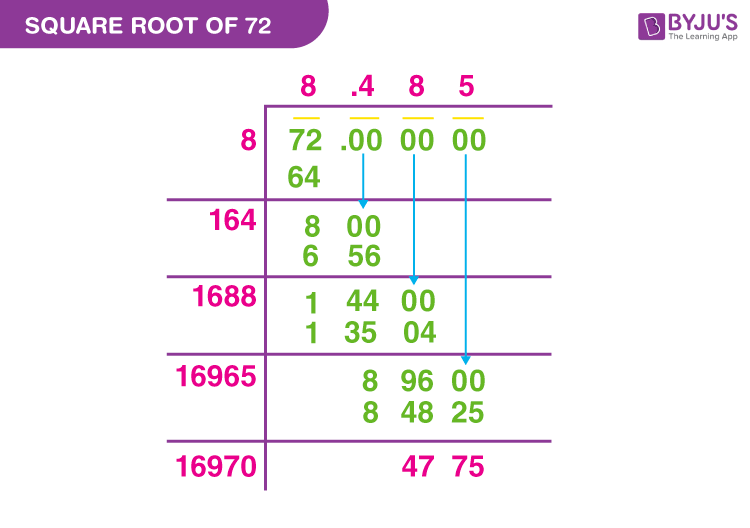
Applications of Simplified Square Roots
Simplified square roots are not just mathematical exercises; they have practical applications in various fields. Here are some examples of how simplified square roots are used in real-world scenarios:
- Engineering: Simplified square roots are crucial in engineering for precise measurements and calculations. For example, in structural engineering, they are used to determine the dimensions and load capacities of structures.
- Physics: In physics, simplified square roots are used to calculate quantities such as velocities and accelerations. For instance, the formula for the time it takes an object to fall from a certain height involves the square root of the height divided by a constant.
- Geometry: Simplifying square roots is often required when dealing with areas and volumes. For example, finding the side length of a square when given its area, or determining the radius of a circle when given its area.
- Astronomy: In astronomy, simplified square roots are used in formulas to calculate distances between celestial bodies and their velocities.
- Car Accident Investigations: Investigators use simplified square roots to determine the speed of vehicles before a crash based on the length of skid marks. The formula involves the square root of the distance multiplied by a constant.
Let's look at some specific examples to understand these applications better:
| Application | Example | Formula |
|---|---|---|
| Free Fall Time | Calculating the time it takes for an object to fall from a height of 64 feet. | \(\frac{\sqrt{64}}{4} = 2 \text{ seconds}\) |
| Speed from Skid Marks | Determining the speed of a car from 190 feet of skid marks. | \(\sqrt{24 \cdot 190} \approx 67.5 \text{ mph}\) |
By understanding and applying simplified square roots, one can solve complex real-world problems with ease and accuracy.
Video hướng dẫn cách tốt nhất để đơn giản hóa căn bậc hai của một số, cụ thể là căn bậc hai của 72. Hãy theo dõi để hiểu rõ hơn và áp dụng vào các bài toán thực tế.
Cách Tốt Nhất Để Đơn Giản Hóa Căn Bậc Hai Của Một Số, Căn(72)
READ MORE:
Hướng dẫn chi tiết cách tính căn bậc hai của số 72. Xem video để biết cách thực hiện và hiểu rõ hơn về căn bậc hai.
Cách Tính Căn Bậc Hai Của 72: Sqrt(72)

















