48 Square Root Simplified: Easy Steps to Simplify √48

The process of simplifying the square root of 48 involves finding factors of 48 that are perfect squares. Here's a detailed step-by-step guide:

Step-by-Step Simplification

1. First, find the prime factorization of 48:

   \( 48 = 2^4 \times 3 \)

2. Identify the perfect square factors:

   \( 2^4 = 16 \) is a perfect square.

3. Rewrite 48 as a product of the perfect square and another factor:

   \( 48 = 16 \times 3 \)

4. Use the property of square roots that \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\):

   \(\sqrt{48} = \sqrt{16 \times 3} = \sqrt{16} \times \sqrt{3}\)

5. Simplify the square root of the perfect square:

   \(\sqrt{16} = 4\)

6. Combine the simplified square roots:

   \(\sqrt{48} = 4 \sqrt{3}\)

Final Simplified Form

Thus, the simplified form of the square root of 48 is:

\(\sqrt{48} = 4\sqrt{3}\)

Simplifying square roots is a fundamental skill in mathematics that allows us to express square roots in their simplest form. This process involves breaking down the number inside the square root, known as the radicand, into its prime factors and then simplifying based on the properties of square roots.

Understanding how to simplify square roots is essential for solving various mathematical problems more efficiently and accurately. Let's explore the steps involved in simplifying the square root of 48:

1. Prime Factorization: Begin by finding the prime factors of the radicand. For 48, the prime factors are 2 and 3.
2. Grouping Perfect Squares: Group the prime factors into pairs, as each pair represents a perfect square. For 48, we can group the factors as follows: \(48 = 2 \times 2 \times 2 \times 2 \times 3\) or \(48 = (2 \times 2) \times (2 \times 2) \times 3\).
3. Extracting Perfect Squares: Extract the square root of each pair of prime factors. For instance, \(\sqrt{2^4 \times 3} = \sqrt{(2^2)^2 \times 3} = 2^2 \sqrt{3}\).
4. Simplifying: Simplify the expression by multiplying the extracted square roots. In our example, \(\sqrt{48} = 4 \sqrt{3}\).

By following these steps, we can simplify square roots efficiently. Simplifying the square root of 48 gives us \(4 \sqrt{3}\), which is much easier to work with in mathematical expressions and calculations.

In the following sections, we will delve deeper into each step of the process, providing detailed explanations and additional examples to ensure a thorough understanding of simplifying square roots.

A square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical terms, the square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). The square root symbol is represented as \( \sqrt{} \), and finding the square root of a number is essentially the opposite of squaring that number.

For example, \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \). Similarly, \( \sqrt{49} = 7 \) because \( 7 \times 7 = 49 \). It is important to note that every positive number has two square roots: one positive and one negative. For instance, both 7 and -7 are square roots of 49 because \( 7 \times 7 = 49 \) and \( -7 \times -7 = 49 \).

When dealing with square roots, there are several key points to remember:

• Perfect Squares: Numbers like 1, 4, 9, 16, 25, and 36 are perfect squares because their square roots are whole numbers.
• Non-Perfect Squares: Numbers that are not perfect squares have square roots that are irrational numbers, which cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal expansions. For example, \( \sqrt{2} \approx 1.414 \).
• Square Root Properties: The product of square roots can be simplified using the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). For instance, \( \sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2 \sqrt{3} \).

Let's consider the square root of 48 as an example:

1. Prime Factorization: Find the prime factors of 48: \( 48 = 2^4 \times 3 \).
2. Grouping Factors: Group the prime factors into pairs: \( 48 = (2^2) \times (2^2) \times 3 \).
3. Simplifying: Apply the square root to each group: \( \sqrt{48} = \sqrt{(2^2) \times (2^2) \times 3} = 2 \times 2 \times \sqrt{3} = 4 \sqrt{3} \).

Understanding square roots is crucial for simplifying expressions, solving equations, and analyzing various mathematical and real-world problems. In the following sections, we will explore different methods and techniques for simplifying square roots, starting with the prime factorization method.

The prime factorization method is an efficient way to simplify square roots. This method involves breaking down the number under the square root (called the radicand) into its prime factors and then simplifying the expression. Here’s how you can simplify the square root of 48 using the prime factorization method:

1. Find the Prime Factors of 48:

   Start by dividing 48 by the smallest prime number, which is 2.

   • 48 ÷ 2 = 24
   • 24 ÷ 2 = 12
   • 12 ÷ 2 = 6
   • 6 ÷ 2 = 3
   • 3 ÷ 3 = 1

   Thus, the prime factorization of 48 is \(2^4 \times 3\).

2. Group the Prime Factors:

   Group the prime factors into pairs. Each pair of the same number can be taken out of the square root.

   • \(\sqrt{48} = \sqrt{2^4 \times 3} = \sqrt{(2^2 \times 2^2) \times 3}\)
3. Simplify the Expression:

   Take one number from each pair out of the square root.

   • \(\sqrt{(2^2 \times 2^2) \times 3} = 2 \times 2 \times \sqrt{3} = 4\sqrt{3}\)

Therefore, the simplified form of the square root of 48 is \(4\sqrt{3}\). This method can be applied to any number to find its simplified square root.

To simplify the square root of a number, it is helpful to identify perfect squares within the number. Perfect squares are numbers that are the square of an integer. For instance, 1 (1²), 4 (2²), 9 (3²), and 16 (4²) are all perfect squares.

To find the perfect squares within 48, we follow these steps:

1. List Factors of 48:
   • The factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.
2. Identify Perfect Squares:
   • Among the factors, the perfect squares are: 1, 4, 16.
3. Select the Largest Perfect Square:
   • The largest perfect square factor of 48 is 16.
4. Divide by the Perfect Square:
   • Divide 48 by 16 to get 3 (48 ÷ 16 = 3).
5. Calculate the Square Root:
   • The square root of 16 is 4 (√16 = 4).
6. Combine Results:
   • Combine the square root of 16 and the remaining factor under the square root: √48 = 4√3.

Therefore, the simplified form of the square root of 48 is 4√3. Identifying and using perfect squares in the factorization process simplifies the calculation significantly, providing a clear and concise result.

Rewriting the radicand is a critical step in simplifying square roots. The radicand is the number under the radical sign. To simplify the square root of 48, we need to express 48 in terms of its prime factors and identify the perfect squares. Here’s a step-by-step guide:

1. Identify Prime Factors: Start by breaking down the number 48 into its prime factors. This can be done through repeated division:

   • 48 ÷ 2 = 24
   • 24 ÷ 2 = 12
   • 12 ÷ 2 = 6
   • 6 ÷ 2 = 3
   • 3 ÷ 3 = 1

   So, the prime factorization of 48 is 2 × 2 × 2 × 2 × 3 or \(2^4 \times 3\).

2. Identify Perfect Squares: Look for pairs of prime factors because the square root of a square is a whole number. In this case, we have \(2^4\), which is a perfect square because \(2^4 = (2^2)^2\). Thus, we can rewrite \(2^4\) as \((2^2)^2\) and separate it under the radical:

   \(\sqrt{48} = \sqrt{2^4 \times 3} = \sqrt{(2^2)^2 \times 3} = \sqrt{(2^2)^2} \times \sqrt{3} = 4\sqrt{3}\)

3. Rewrite the Radicand: Now, express the original radicand (48) in its simplified form:

   \(\sqrt{48} = 4\sqrt{3}\)

This method of rewriting the radicand by identifying and simplifying perfect squares helps in reducing the square root to its simplest radical form.

Simplifying the square root of 48 involves breaking down the radicand (the number inside the square root) into its prime factors and then simplifying. Here's a step-by-step guide:

1. Prime Factorization: Start by finding the prime factors of 48. The prime factorization of 48 is:

   \[
   48 = 2 \times 24 = 2 \times 2 \times 12 = 2 \times 2 \times 2 \times 6 = 2 \times 2 \times 2 \times 2 \times 3 = 2^4 \times 3
   \]

2. Grouping the Factors: Group the prime factors into pairs:

   \[
   2^4 \times 3 = (2 \times 2) \times (2 \times 2) \times 3
   \]

3. Applying the Square Root: Take the square root of each pair of factors:

   \[
   \sqrt{48} = \sqrt{(2 \times 2) \times (2 \times 2) \times 3} = \sqrt{2^2 \times 2^2 \times 3}
   \]

   \[
   \sqrt{2^2} \times \sqrt{2^2} \times \sqrt{3} = 2 \times 2 \times \sqrt{3}
   \]

4. Simplifying the Expression: Multiply the simplified factors:

   \[
   2 \times 2 \times \sqrt{3} = 4\sqrt{3}
   \]

Thus, the simplified form of the square root of 48 is:

\[
\sqrt{48} = 4\sqrt{3}
\]

After breaking down the square root of 48 into its prime factors and simplifying, the next step is to combine these simplified factors to get the final simplified form. Let's walk through this process step-by-step:

1. Identify Simplified Factors: From the previous steps, we have identified the factors inside the square root and simplified them:

   \[
   \sqrt{48} = \sqrt{2^4 \times 3}
   \]

2. Separate Perfect Squares: Separate the perfect squares from the other factors:

   \[
   \sqrt{2^4 \times 3} = \sqrt{(2^2 \times 2^2) \times 3}
   \]

3. Take the Square Root of Perfect Squares: Take the square root of the perfect squares (since \(\sqrt{a^2} = a\)):

   \[
   \sqrt{2^2} \times \sqrt{2^2} \times \sqrt{3} = 2 \times 2 \times \sqrt{3}
   \]

4. Combine the Factors: Multiply the simplified factors outside the square root:

   \[
   2 \times 2 \times \sqrt{3} = 4\sqrt{3}
   \]

Therefore, the combined simplified factors of the square root of 48 give us the final simplified form:

\[
\sqrt{48} = 4\sqrt{3}
\]

To determine the final simplified form of the square root of 48, we consolidate the steps we have previously covered. Here's the detailed process:

1. Prime Factorization: Start by finding the prime factorization of 48:

   \[
   48 = 2^4 \times 3
   \]

2. Separate the Perfect Squares: Identify the perfect squares within the prime factorization:

   \[
   \sqrt{48} = \sqrt{2^4 \times 3} = \sqrt{(2^2)^2 \times 3}
   \]

3. Extract the Perfect Squares: Take the square root of the perfect squares:

   \[
   \sqrt{(2^2)^2 \times 3} = 2^2 \times \sqrt{3} = 4 \sqrt{3}
   \]

After extracting and simplifying the factors, we arrive at the final simplified form:

\[
\sqrt{48} = 4\sqrt{3}
\]

This means that the square root of 48, when simplified, is \(4\sqrt{3}\). This form is much easier to work with in various mathematical applications and helps in understanding the underlying structure of the number.

Simplifying the square root of 48 can be done in a clear and structured manner. Here is a detailed, step-by-step process to achieve the final simplified form:

1. Find the Prime Factorization:

   First, find the prime factors of 48:

   \[
   48 = 2 \times 24 = 2 \times 2 \times 12 = 2 \times 2 \times 2 \times 6 = 2 \times 2 \times 2 \times 2 \times 3 = 2^4 \times 3
   \]

2. Express Under the Square Root:

   Rewrite the square root of 48 using its prime factorization:

   \[
   \sqrt{48} = \sqrt{2^4 \times 3}
   \]

3. Identify Perfect Squares:

   Group the factors to identify perfect squares. In this case, \(2^4\) is a perfect square:

   \[
   \sqrt{2^4 \times 3} = \sqrt{(2^2)^2 \times 3}
   \]

4. Simplify the Perfect Squares:

   Take the square root of the perfect squares:

   \[
   \sqrt{(2^2)^2 \times 3} = 2^2 \times \sqrt{3} = 4 \sqrt{3}
   \]

5. Combine the Factors:

   Combine the simplified factors to get the final form:

   \[
   4 \sqrt{3}
   \]

Thus, the step-by-step simplification process of the square root of 48 yields:

\[
\sqrt{48} = 4\sqrt{3}
\]

Following these steps ensures that the square root is simplified correctly, making it easier to use in further mathematical calculations and applications.

When simplifying the square root of 48, it's easy to make mistakes that can lead to incorrect results. Here are some common pitfalls to watch out for and how to avoid them:

1. Incorrect Prime Factorization:

   Ensure that the prime factorization of 48 is done correctly. An error in this step can lead to incorrect simplification:

   \[
   48 = 2^4 \times 3
   \]

2. Not Grouping Factors Properly:

   Failing to correctly group the factors to identify perfect squares can lead to mistakes. Make sure to group pairs of prime factors:

   \[
   \sqrt{2^4 \times 3} = \sqrt{(2^2)^2 \times 3}
   \]

3. Ignoring Perfect Squares:

   Overlooking perfect squares in the factorization prevents proper simplification. Always simplify perfect squares:

   \[
   \sqrt{(2^2)^2 \times 3} = 2^2 \times \sqrt{3} = 4 \sqrt{3}
   \]

4. Incorrectly Simplifying Non-Perfect Squares:

   Remember that only perfect squares can be simplified outside the square root. Ensure correct simplification:

   \[
   \sqrt{4 \times 3} \neq \sqrt{4} \times \sqrt{3}
   \]

5. Arithmetic Errors:

   Basic arithmetic mistakes, such as multiplying or adding incorrectly, can lead to errors in the final result. Double-check your calculations:

   \[
   2 \times 2 = 4
   \]

Avoiding these common mistakes will help ensure that the simplification process is accurate and that the final result is correct:

\[
\sqrt{48} = 4\sqrt{3}
\]

Simplified square roots are not just an academic exercise; they have practical applications in various fields. Here are some ways in which understanding and using simplified square roots can be beneficial:

1. Geometry and Trigonometry:

   Simplified square roots often appear in geometric formulas, such as the Pythagorean theorem, which is used to find the lengths of sides in right-angled triangles:

   \[
   c = \sqrt{a^2 + b^2}
   \]

   If \(a = 6\) and \(b = 8\), then:

   \[
   c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10
   \]

2. Physics:

   Square roots are used in various physics equations. For example, the formula for the period \(T\) of a pendulum involves the square root:

   \[
   T = 2\pi \sqrt{\frac{L}{g}}
   \]

   where \(L\) is the length of the pendulum and \(g\) is the acceleration due to gravity.

3. Engineering:

   Engineers use simplified square roots in calculations involving stress, strain, and other properties of materials. For instance, the formula for calculating the natural frequency of a beam involves a square root:

   \[
   f = \frac{1}{2\pi} \sqrt{\frac{k}{m}}
   \]

   where \(k\) is the stiffness and \(m\) is the mass.

4. Architecture:

   Architects use square roots in their designs to ensure structural integrity and aesthetic proportions. Calculations involving the dimensions of different shapes and structures often require the use of simplified square roots.

5. Finance:

   In finance, the square root is used in the calculation of standard deviation and other statistical measures that assess market volatility and risk:

   \[
   \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2}
   \]

   where \(\sigma\) is the standard deviation, \(N\) is the number of data points, \(x_i\) are the data points, and \(\mu\) is the mean of the data points.

Understanding how to simplify square roots makes these applications more manageable and easier to compute, facilitating accuracy and efficiency in various professional fields.

Visualizing the simplification of the square root of 48 can help in understanding the process better. Here's a step-by-step visual representation:

1. Prime Factorization:

   Break down 48 into its prime factors:

   \[
   48 = 2 \times 24 = 2 \times 2 \times 12 = 2 \times 2 \times 2 \times 6 = 2 \times 2 \times 2 \times 2 \times 3 = 2^4 \times 3
   \]

   

2. Group the Factors:

   Group the prime factors into pairs of perfect squares:

   \[
   \sqrt{48} = \sqrt{2^4 \times 3} = \sqrt{(2^2)^2 \times 3}
   \]

   

3. Take the Square Root:

   Simplify by taking the square root of each pair of perfect squares:

   \[
   \sqrt{(2^2)^2 \times 3} = 2^2 \times \sqrt{3} = 4 \sqrt{3}
   \]

   

4. Combine the Simplified Factors:

   Combine the factors to get the final simplified form:

   \[
   4 \sqrt{3}
   \]

   

The final simplified form of the square root of 48 is:

\[
\sqrt{48} = 4\sqrt{3}
\]

Using visual aids can make the simplification process more intuitive and help solidify understanding of the steps involved.

In this section, we will explore additional examples of simplifying square roots using the prime factorization method. Simplifying square roots can help in understanding the properties of numbers and making calculations easier. Below are a few examples with detailed step-by-step solutions.

Example 1: Simplifying √75

1. Find the prime factorization of 75:
   • 75 = 3 × 5 × 5
2. Identify pairs of prime factors:
   • We have one pair of 5s.
3. Rewrite the radicand using the pairs:
   • √75 = √(3 × 5²)
4. Take the square root of the pair:
   • √(3 × 5²) = 5√3
5. The simplified form of √75 is:
   • 5√3

Example 2: Simplifying √200

1. Find the prime factorization of 200:
   • 200 = 2 × 2 × 2 × 5 × 5
2. Identify pairs of prime factors:
   • We have one pair of 2s and one pair of 5s.
3. Rewrite the radicand using the pairs:
   • √200 = √(2² × 5² × 2)
4. Take the square root of the pairs:
   • √(2² × 5² × 2) = 2 × 5 √2
5. The simplified form of √200 is:
   • 10√2

Example 3: Simplifying √98

1. Find the prime factorization of 98:
   • 98 = 2 × 7 × 7
2. Identify pairs of prime factors:
   • We have one pair of 7s.
3. Rewrite the radicand using the pairs:
   • √98 = √(2 × 7²)
4. Take the square root of the pair:
   • √(2 × 7²) = 7√2
5. The simplified form of √98 is:
   • 7√2

Example 4: Simplifying √180

1. Find the prime factorization of 180:
   • 180 = 2 × 2 × 3 × 3 × 5
2. Identify pairs of prime factors:
   • We have one pair of 2s and one pair of 3s.
3. Rewrite the radicand using the pairs:
   • √180 = √(2² × 3² × 5)
4. Take the square root of the pairs:
   • √(2² × 3² × 5) = 2 × 3 √5
5. The simplified form of √180 is:
   • 6√5

Example 5: Simplifying √245

1. Find the prime factorization of 245:
   • 245 = 5 × 7 × 7
2. Identify pairs of prime factors:
   • We have one pair of 7s.
3. Rewrite the radicand using the pairs:
   • √245 = √(5 × 7²)
4. Take the square root of the pair:
   • √(5 × 7²) = 7√5
5. The simplified form of √245 is:
   • 7√5

In this section, we will provide practice problems along with their detailed solutions to help you master the process of simplifying square roots. Each problem will be broken down step-by-step to ensure clarity and understanding.

Practice Problem 1: Simplify √72

1. Find the prime factorization of 72:
   • 72 = 2 × 2 × 2 × 3 × 3
2. Identify pairs of prime factors:
   • We have one pair of 2s and one pair of 3s.
3. Rewrite the radicand using the pairs:
   • √72 = √(2² × 3² × 2)
4. Take the square root of the pairs:
   • √(2² × 3² × 2) = 2 × 3 √2
5. The simplified form of √72 is:
   • 6√2

Practice Problem 2: Simplify √108

1. Find the prime factorization of 108:
   • 108 = 2 × 2 × 3 × 3 × 3
2. Identify pairs of prime factors:
   • We have one pair of 2s and one pair of 3s.
3. Rewrite the radicand using the pairs:
   • √108 = √(2² × 3² × 3)
4. Take the square root of the pairs:
   • √(2² × 3² × 3) = 2 × 3 √3
5. The simplified form of √108 is:
   • 6√3

Practice Problem 3: Simplify √288

1. Find the prime factorization of 288:
   • 288 = 2 × 2 × 2 × 2 × 3 × 3
2. Identify pairs of prime factors:
   • We have two pairs of 2s and one pair of 3s.
3. Rewrite the radicand using the pairs:
   • √288 = √(2² × 2² × 3²)
4. Take the square root of the pairs:
   • √(2² × 2² × 3²) = 2 × 2 × 3
5. The simplified form of √288 is:
   • 12

Practice Problem 4: Simplify √450

1. Find the prime factorization of 450:
   • 450 = 2 × 3 × 3 × 5 × 5
2. Identify pairs of prime factors:
   • We have one pair of 3s and one pair of 5s.
3. Rewrite the radicand using the pairs:
   • √450 = √(2 × 3² × 5²)
4. Take the square root of the pairs:
   • √(2 × 3² × 5²) = 3 × 5 √2
5. The simplified form of √450 is:
   • 15√2

Practice Problem 5: Simplify √125

1. Find the prime factorization of 125:
   • 125 = 5 × 5 × 5
2. Identify pairs of prime factors:
   • We have one pair of 5s.
3. Rewrite the radicand using the pairs:
   • √125 = √(5² × 5)
4. Take the square root of the pair:
   • √(5² × 5) = 5 √5
5. The simplified form of √125 is:
   • 5√5

Here are some frequently asked questions about simplifying square roots:

• What is the square root of 48?

  The square root of 48 is approximately 6.928. In its simplified radical form, it is \( 4\sqrt{3} \).

• Can we find the square root of 48 by the approximation method?

  Yes, we can estimate the square root of 48 using the approximation method. This method involves recognizing that 48 lies between the perfect squares of 36 (6²) and 49 (7²), so the square root of 48 is between 6 and 7.

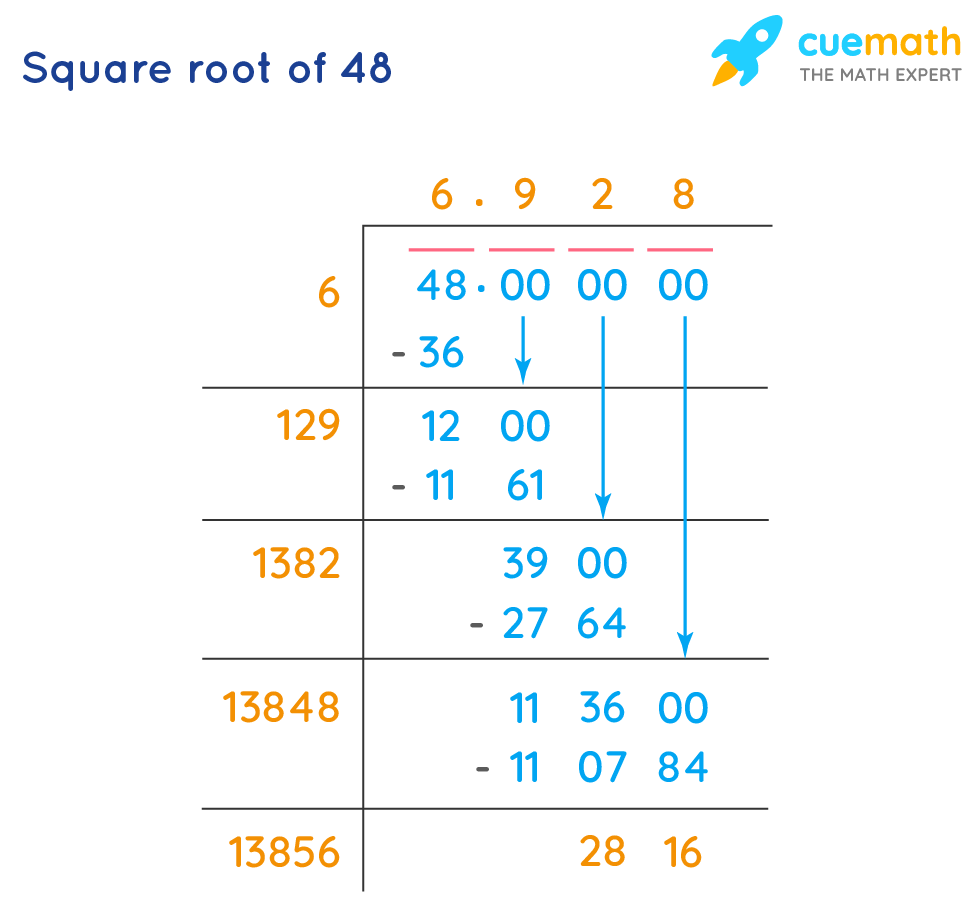
• How do you find the square root of 48?

  There are several methods to find the square root of 48:
  

  
  
  1. Prime Factorization Method: Decompose 48 into its prime factors (2 × 2 × 2 × 2 × 3) and group the factors to simplify \( \sqrt{48} \) to \( 4\sqrt{3} \).
  
  
  2. Long Division Method: Use the long division method to iteratively approximate the square root.
  
  
  3. Estimation Method: Estimate based on nearby perfect squares.
  
  
  
  


• Is the square root of 48 an irrational number?

  Yes, the square root of 48 is an irrational number because it cannot be expressed as a simple fraction and its decimal representation is non-terminating and non-repeating.

• What is the square root of 48 in simplified form?

  The square root of 48 in simplified form is \( 4\sqrt{3} \).

• Is the square root of 48 a natural number?

  No, the square root of 48 is not a natural number. Natural numbers are positive integers, and \( \sqrt{48} \approx 6.928 \) is not an integer.

• Is the square root of 48 a perfect square?

  No, 48 is not a perfect square because its square root is not an integer.

In conclusion, simplifying the square root of 48 involves breaking down the number into its prime factors and identifying perfect squares within those factors. The process highlights the importance of understanding prime factorization and the properties of square roots.

We started with the number 48 and determined its prime factorization: \(48 = 2^4 \times 3\). By identifying the perfect square \(16 = 2^4\), we were able to simplify \(\sqrt{48}\) to \(4\sqrt{3}\). This simplified form is more manageable and often used in further mathematical applications.

Understanding how to simplify square roots is not only useful in theoretical mathematics but also in practical scenarios, such as solving quadratic equations and evaluating integrals in calculus. It helps in reducing complexity and making calculations more straightforward.

We hope this comprehensive guide has provided you with a clear and detailed understanding of how to simplify the square root of 48 and apply similar methods to other numbers. With practice, these techniques will become second nature, aiding in your overall mathematical proficiency.

Thank you for following along, and we encourage you to continue exploring more complex mathematical concepts and their practical applications. Happy learning!