Topic square root 28 simplified: Unlock the mystery of simplifying the square root of 28 with our easy-to-follow guide. In this article, you'll learn the step-by-step process to simplify √28, understand the underlying concepts, and apply this knowledge in practical scenarios. Perfect for students and math enthusiasts alike, this guide makes simplifying square roots simple and fun!
Table of Content
- Square Root of 28 Simplified
- Introduction to Square Roots
- Understanding Square Root Simplification
- Prime Factorization Method
- Simplifying Square Root of 28 Step-by-Step
- Mathematical Explanation and Proof
- Alternative Methods for Simplifying Square Roots
- Common Mistakes to Avoid
- Practical Applications of Simplified Square Roots
- Additional Practice Problems
- Conclusion
- YOUTUBE:
Square Root of 28 Simplified
The square root of 28 simplified is represented as:
Here, the expression \( 2\sqrt{7} \) is the simplified form of \( \sqrt{28} \). In this form, the square root of 28 cannot be simplified further into an integer or a simpler radical.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5, because \(5 \times 5 = 25\).
Mathematically, the square root of a number \(x\) is denoted as \(\sqrt{x}\). The principal square root is the non-negative root, which is what we typically refer to when we mention the square root of a number.
Here is a simple table to illustrate some basic square roots:
| Number | Square Root |
|---|---|
| 1 | \(\sqrt{1} = 1\) |
| 4 | \(\sqrt{4} = 2\) |
| 9 | \(\sqrt{9} = 3\) |
| 16 | \(\sqrt{16} = 4\) |
| 25 | \(\sqrt{25} = 5\) |
When simplifying square roots, the goal is to find the simplest radical form of the number. This often involves breaking down the number into its prime factors. For instance, to simplify the square root of 28, we can use the following steps:
- Find the prime factorization of 28: \(28 = 2 \times 2 \times 7\).
- Group the prime factors into pairs: \(28 = (2 \times 2) \times 7\).
- Simplify the expression using the property \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\): \(\sqrt{28} = \sqrt{(2 \times 2) \times 7} = \sqrt{2^2 \times 7} = \sqrt{2^2} \times \sqrt{7}\).
- Since \(\sqrt{2^2} = 2\), we have: \(\sqrt{28} = 2 \sqrt{7}\).
By following these steps, we find that the square root of 28 simplifies to \(2 \sqrt{7}\). This method can be applied to simplify the square root of any non-perfect square number.
Understanding Square Root Simplification
Simplifying square roots involves expressing the square root of a number in its simplest form. This process makes calculations easier and the results more comprehensible. Here’s a detailed explanation of how to simplify square roots:
Steps to Simplify Square Roots
-
Identify the number inside the square root, known as the radicand. For example, in √28, the radicand is 28.
-
Perform prime factorization on the radicand to break it down into its prime factors. Prime factorization of 28 is:
- 28 = 2 × 14
- 14 = 2 × 7
- So, 28 = 2 × 2 × 7 or 28 = 2² × 7
-
Group the prime factors into pairs. For each pair of prime factors, take one factor out of the square root. If a prime factor does not have a pair, it remains inside the square root:
- √28 = √(2² × 7)
- Since 2² is a pair of 2s, take one 2 out of the square root:
- √28 = 2√7
Example
Let’s go through the example of simplifying √28 step-by-step:
- Start with the radicand: 28
- Perform prime factorization: 28 = 2 × 2 × 7
- Group the prime factors: 2² × 7
- Take one factor out of the square root for each pair: 2√7
- Therefore, √28 simplifies to 2√7
Properties of Simplified Square Roots
Simplified square roots have the following properties:
- The radicand has no perfect square factors other than 1.
- The expression is in its simplest form, which is easier to work with in mathematical calculations.
Benefits of Simplifying Square Roots
Understanding how to simplify square roots is beneficial because:
- It makes calculations involving square roots more manageable.
- It provides a clearer understanding of the magnitude of the square root.
- It helps in comparing and combining square roots more easily.
Prime Factorization Method
The prime factorization method is a reliable technique to simplify square roots by breaking down the radicand into its prime factors. This method ensures that the square root is expressed in its simplest form. Here’s a detailed step-by-step guide on using the prime factorization method to simplify the square root of 28:
Steps for Prime Factorization
-
Identify the radicand: The number inside the square root is called the radicand. For our example, the radicand is 28.
-
Perform prime factorization: Break down 28 into its prime factors. Begin by dividing 28 by the smallest prime number, 2:
- 28 ÷ 2 = 14
- 14 ÷ 2 = 7
- Since 7 is a prime number, it cannot be divided further.
So, the prime factorization of 28 is \(28 = 2 \times 2 \times 7\) or \(28 = 2^2 \times 7\).
-
Group the prime factors: Group the prime factors into pairs. For every pair of the same prime factor, one factor can be taken out of the square root:
- \(\sqrt{28} = \sqrt{2^2 \times 7}\)
-
Simplify the square root: For each pair of prime factors, take one factor out of the square root:
- \(\sqrt{2^2 \times 7} = 2\sqrt{7}\)
Example of Simplifying √28
Let’s apply the prime factorization method to simplify \(\sqrt{28}\):
- Start with the radicand: 28
- Perform prime factorization: \(28 = 2^2 \times 7\)
- Group the prime factors: \(2^2 \times 7\)
- Simplify the square root: \(\sqrt{2^2 \times 7} = 2\sqrt{7}\)
Therefore, \(\sqrt{28}\) simplifies to \(2\sqrt{7}\).
Benefits of Prime Factorization
The prime factorization method is beneficial because:
- It systematically breaks down the radicand into its basic components.
- It makes it easier to identify and extract perfect square factors.
- It ensures the square root is simplified to its most basic form.
Simplifying Square Root of 28 Step-by-Step
Simplifying the square root of 28 involves a systematic process of breaking down the number into its prime factors and then simplifying the expression. Follow these detailed steps to simplify \(\sqrt{28}\):
Step-by-Step Process
-
Identify the radicand: The radicand is the number inside the square root symbol. For our example, the radicand is 28.
-
Perform prime factorization: Break down 28 into its prime factors.
- Start by dividing 28 by the smallest prime number, which is 2: \(28 \div 2 = 14\)
- Continue dividing by 2: \(14 \div 2 = 7\)
- Since 7 is a prime number, it cannot be divided further.
Therefore, the prime factorization of 28 is \(28 = 2 \times 2 \times 7\) or \(28 = 2^2 \times 7\).
-
Group the prime factors: Group the prime factors into pairs.
- In this case, we have \(2^2\) and 7.
The expression inside the square root now looks like this: \(\sqrt{2^2 \times 7}\).
-
Simplify the square root: For each pair of the same prime factor, take one factor out of the square root.
- \(\sqrt{2^2 \times 7} = 2\sqrt{7}\)
Conclusion
By following these steps, we have simplified the square root of 28. The final simplified form is:
\(\sqrt{28} = 2\sqrt{7}\)
Summary of Steps
- Identify the radicand: 28
- Perform prime factorization: \(28 = 2^2 \times 7\)
- Group the prime factors: \(2^2\) and 7
- Simplify the square root: \(\sqrt{2^2 \times 7} = 2\sqrt{7}\)
Thus, we have successfully simplified \(\sqrt{28}\) to \(2\sqrt{7}\) using a clear and methodical approach.

Mathematical Explanation and Proof
To simplify the square root of 28, we can use the method of prime factorization. Let's break it down step by step:
Prime Factorization of 28: First, we find the prime factors of 28.
- 28 is divisible by 2: \(28 \div 2 = 14\)
- 14 is divisible by 2: \(14 \div 2 = 7\)
- 7 is a prime number.
So, the prime factorization of 28 is \(2 \times 2 \times 7\).
Grouping the Prime Factors: We group the prime factors in pairs.
The prime factors of 28 are \(2 \times 2 \times 7\), which can be grouped as \((2 \times 2) \times 7\).
Taking the Square Root: Apply the square root to the grouped prime factors.
\(\sqrt{28} = \sqrt{2 \times 2 \times 7} = \sqrt{(2 \times 2) \times 7} = \sqrt{2^2 \times 7}\)
Simplifying the Expression: Simplify the square root by separating the square root of the perfect square and the remaining factor.
\(\sqrt{2^2 \times 7} = \sqrt{2^2} \times \sqrt{7} = 2\sqrt{7}\)
Therefore, the simplified form of \(\sqrt{28}\) is \(2\sqrt{7}\).
Proof:
To verify our simplification, we can square the simplified result and check if we get back to 28.
- Square the simplified form: \((2\sqrt{7})^2 = 2^2 \times (\sqrt{7})^2 = 4 \times 7 = 28\).
Since squaring \(2\sqrt{7}\) gives us 28, our simplification is correct.
Alternative Methods for Simplifying Square Roots
There are several methods to simplify square roots, each offering a unique approach to achieving the simplest radical form. Below, we will explore some of these alternative methods.
1. Prime Factorization Method
This method involves breaking down the number inside the square root into its prime factors.
- Find the prime factors of the number under the square root.
- Group the prime factors into pairs.
- Move one factor from each pair outside the square root.
Example: To simplify \(\sqrt{28}\):
\[
\sqrt{28} = \sqrt{2 \times 2 \times 7} = 2\sqrt{7}
\]
2. Long Division Method
This method is particularly useful for finding the square root of a number that isn't a perfect square. It involves a series of division steps to approximate the square root.
- Group the digits of the number in pairs, starting from the decimal point.
- Find the largest number whose square is less than or equal to the first group.
- Use the result to form a new divisor and repeat the process with the next group of digits.
This method can be repeated to get a more accurate approximation of the square root.
3. Repeated Subtraction Method
This ancient method involves repeatedly subtracting consecutive odd numbers from the number for which you are finding the square root until you reach zero.
- Start with the number and subtract consecutive odd numbers (1, 3, 5, ...).
- Count the number of subtractions performed to reach zero.
Example: To find \(\sqrt{28}\):
\[
28 - 1 = 27 \\
27 - 3 = 24 \\
24 - 5 = 19 \\
19 - 7 = 12 \\
12 - 9 = 3 \\
3 - 11 = -8 \text{ (stop here, as the next step would go below zero)}
\]
Since the count of subtractions is not an integer, this method indicates that \(\sqrt{28}\) is not a perfect square and requires approximation.
4. Using Calculator Approximation
For practical purposes, especially when a precise decimal value is needed, using a calculator is often the quickest method.
- Enter the number into a calculator and press the square root function.
Example: The square root of 28 using a calculator is approximately 5.2915.
5. Graphical Method
This visual method involves plotting the number on a number line and estimating its square root based on known squares.
- Identify the nearest perfect squares below and above the number.
- Estimate the square root based on these values.
Example: Knowing that \( \sqrt{25} = 5 \) and \( \sqrt{36} = 6 \), we estimate \( \sqrt{28} \) to be slightly more than 5 but less than 6.
By using these various methods, you can simplify square roots effectively depending on the context and the tools available.
Common Mistakes to Avoid
When simplifying square roots, there are several common mistakes that students often make. Here are some key errors to watch out for and tips on how to avoid them:
- Incorrect Prime Factorization: Make sure to break down the number completely into its prime factors. For example, the correct prime factorization of 28 is \( 28 = 2 \times 2 \times 7 \), not \( 28 = 4 \times 7 \).
- Forgetting to Pair Factors: When simplifying square roots, you need to pair the prime factors. In the case of \( \sqrt{28} \), the correct pairs are \( 2 \times 2 \). This pair comes out of the square root as a single 2.
- Leaving Unpaired Factors Inside the Square Root: Any prime factor that does not have a pair must stay inside the square root. For \( \sqrt{28} \), the factor 7 remains inside because it is unpaired.
- Incorrect Simplification: Ensure that you correctly simplify the expression after factoring. For \( \sqrt{28} \), the simplification should be \( \sqrt{2 \times 2 \times 7} = 2\sqrt{7} \), not \( 4\sqrt{7} \).
- Not Using Simplified Form: Always express the final answer in the simplest form. For example, always write \( 2\sqrt{7} \) instead of \( \sqrt{28} \) after simplification.
By being mindful of these common mistakes, you can ensure accurate and simplified square root calculations.
Practical Applications of Simplified Square Roots
Simplified square roots, such as \( \sqrt{28} = 2\sqrt{7} \), are not merely abstract mathematical concepts but have numerous practical applications across various fields. Understanding these applications can enhance our appreciation of the relevance and utility of square roots in everyday life and professional contexts. Here are some detailed examples:
-
Geometry and Architecture:
In geometry, simplified square roots are crucial for solving problems involving the Pythagorean theorem. For instance, the hypotenuse of a right triangle with legs of lengths \( \sqrt{28} \) and another side can be easily calculated. In architecture, the accurate calculation of diagonal distances and structural dimensions often involves square roots.
-
Physics and Engineering:
Simplified square roots play a significant role in physics for calculating distances, velocities, and forces. In engineering, particularly civil and structural engineering, they are used to determine the natural frequencies of structures, aiding in the design of buildings and bridges to withstand dynamic loads such as winds and earthquakes.
-
Statistics and Probability:
Square roots are fundamental in statistical analysis. The standard deviation, a measure of data dispersion, is the square root of the variance. Simplifying square roots helps in presenting and interpreting statistical data more clearly.
-
Computer Science:
In computer graphics and gaming, simplified square roots are used to calculate distances between points and vector magnitudes. Algorithms for encryption and data compression also utilize square roots to enhance efficiency and security.
-
Navigation:
Pilots and navigators use square roots to compute distances between waypoints. The distance formula, derived from the Pythagorean theorem, is essential for accurate navigation in both aviation and maritime contexts.
-
Telecommunications:
In telecommunications, the inverse square law, which describes how signal strength diminishes with distance, involves square roots. Understanding and simplifying these roots helps in designing efficient communication networks.
These examples illustrate the diverse applications of simplified square roots, emphasizing their importance in both theoretical and practical scenarios. Mastering the simplification of square roots can therefore provide valuable skills applicable in numerous professional fields and everyday situations.
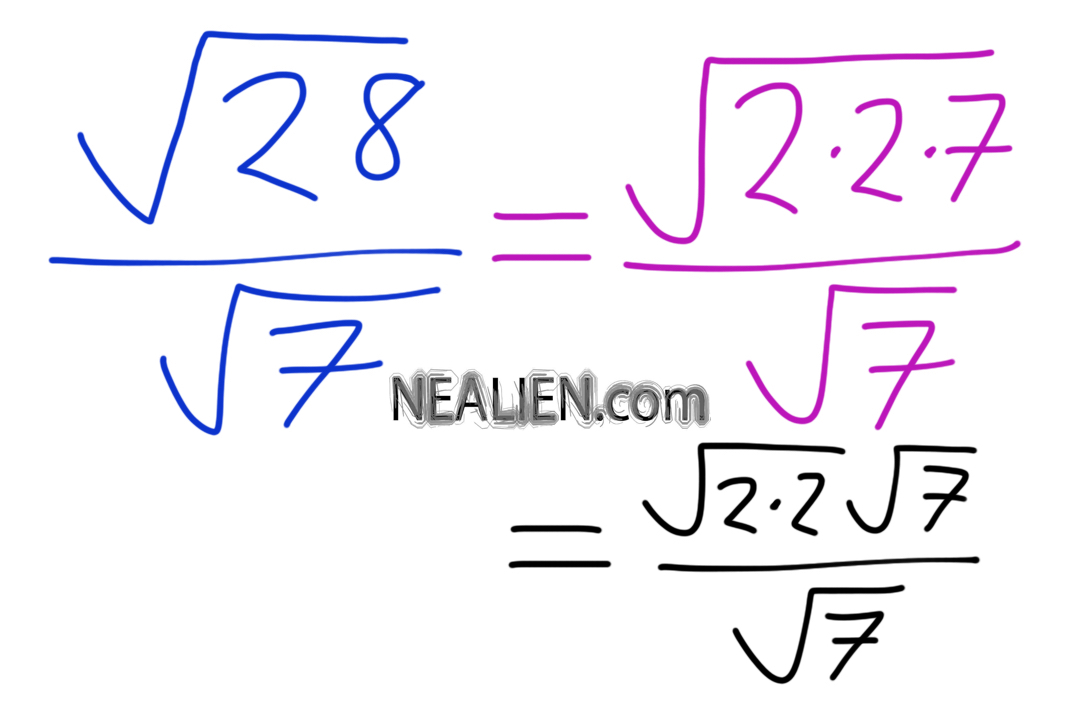
Additional Practice Problems
Below are some additional practice problems to help you master the art of simplifying square roots. Work through each problem step-by-step to ensure you understand the process.
-
Problem 1: Simplify √50
- Find the prime factorization of 50: 50 = 2 × 5 × 5
- Group the prime factors into pairs: √(2 × 52)
- Simplify by taking out the pair: 5√2
-
Problem 2: Simplify √72
- Find the prime factorization of 72: 72 = 2 × 2 × 2 × 3 × 3
- Group the prime factors into pairs: √(22 × 2 × 32)
- Simplify by taking out the pairs: 6√2
-
Problem 3: Simplify √98
- Find the prime factorization of 98: 98 = 2 × 7 × 7
- Group the prime factors into pairs: √(2 × 72)
- Simplify by taking out the pair: 7√2
-
Problem 4: Simplify √200
- Find the prime factorization of 200: 200 = 2 × 2 × 2 × 5 × 5
- Group the prime factors into pairs: √(22 × 2 × 52)
- Simplify by taking out the pairs: 10√2
Practice these problems and try to create similar ones to further enhance your understanding. With consistent practice, simplifying square roots will become second nature.
Conclusion
In this article, we have explored the process of simplifying the square root of 28 using various mathematical techniques. By breaking down the number into its prime factors, we determined that the square root of 28 can be expressed in its simplest form as \(2\sqrt{7}\).
This simplification process not only helps in making calculations easier but also provides a deeper understanding of the properties of square roots and their applications. The steps involved—factorizing the number, grouping the prime factors, and simplifying the expression—are essential tools in algebra that can be applied to other similar problems.
We also touched upon alternative methods, such as the long division method, which offers a detailed approach to finding the square root of any number, including those that result in irrational numbers. Understanding these methods broadens our mathematical toolkit and enhances problem-solving skills.
By avoiding common mistakes, such as incorrect factorization or mishandling the properties of square roots, we can ensure accurate results. Practical applications of simplified square roots are vast, from solving quadratic equations to simplifying expressions in physics and engineering.
As you continue to practice and apply these techniques, you will find that simplifying square roots becomes a straightforward and valuable skill. Keep exploring and practicing with additional problems to reinforce your understanding and proficiency.
Mathematics is a progressive journey of learning and discovery. Simplifying the square root of 28 is just one example of how breaking down complex problems into simpler steps can lead to clear and precise solutions. Keep challenging yourself with new problems, and enjoy the process of mathematical exploration and mastery.
Căn Bậc Hai của 28
READ MORE:
Cách Đơn Giản Hóa Căn Bậc Hai















