Topic 3 square root of 27: Delve into the fascinating world of roots with our comprehensive guide on the "3 square root of 27". Discover how to calculate both the cube and square roots, explore their unique properties, and understand their practical applications. Whether you're a student or just curious, this article will illuminate the intriguing aspects of roots in mathematics.
Table of Content
- Understanding the Cube Root of 27
- Introduction to Square Roots and Cube Roots
- What is the Cube Root?
- What is the Square Root?
- How to Calculate the Cube Root of 27
- Steps to Find the Square Root of 27
- Properties of Cube Roots
- Properties of Square Roots
- Examples of Cube Roots
- Examples of Square Roots
- Applications of Cube Roots in Real Life
- Applications of Square Roots in Real Life
- Common Mistakes in Calculating Roots
- Understanding the Relationship Between Cubes and Cube Roots
- Understanding the Relationship Between Squares and Square Roots
- Mathematical Notation and Symbols for Roots
- Using Technology to Calculate Roots
- Practice Problems for Cube Roots
- Practice Problems for Square Roots
- YOUTUBE: Xem video để học cách tìm căn bậc ba của 8 và 27 một cách dễ dàng và không cần dùng máy tính.
Understanding the Cube Root of 27
The cube root of a number is a value that, when multiplied by itself three times, gives the original number. In mathematical notation, the cube root of a number \( n \) is written as \( \sqrt[3]{n} \).
Calculation
To find the cube root of 27, we need to determine the number \( x \) such that:
\( x^3 = 27 \)
Using the cube root function, this can be represented as:
\( \sqrt[3]{27} \)
Step-by-Step Solution
1. Identify the number: \( 27 \).
2. Recognize that 27 is a perfect cube.
3. Determine which number, when cubed, equals 27:
- \( 3 \times 3 = 9 \)
- \( 9 \times 3 = 27 \)
Thus, the cube root of 27 is:
\( \sqrt[3]{27} = 3 \)
Verifying the Result
To verify, we cube the result:
\( 3^3 = 3 \times 3 \times 3 = 27 \)
This confirms that \( 3 \) is indeed the cube root of 27.
General Properties
- The cube root function is the inverse of the cube function.
- Cube roots of positive numbers are positive.
- Cube roots of negative numbers are negative.
Conclusion
The cube root of 27 is a straightforward example of finding roots of perfect cubes. In this case, the cube root of 27 is 3, as demonstrated by the calculations above.

READ MORE:
Introduction to Square Roots and Cube Roots
The concepts of square roots and cube roots are fundamental in mathematics, offering a deeper understanding of numbers and their properties. In this section, we will explore what these roots are, how to calculate them, and their significance in various mathematical contexts.
Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol (√). For example, the square root of 27 can be expressed as:
\[\sqrt{27}\]
Calculating the square root of 27, we find it is approximately 5.196.
Cube Roots
The cube root of a number is a value that, when used three times in a multiplication, gives the original number. It is denoted by the radical symbol with an index of three (∛). For example, the cube root of 27 can be expressed as:
\[\sqrt[3]{27}\]
Calculating the cube root of 27, we find it is exactly 3.
To summarize, the primary difference between square roots and cube roots lies in the exponent to which the root value must be raised to obtain the original number. Square roots involve an exponent of 2, while cube roots involve an exponent of 3.
Mathematical Notation
- Square root of a number \(x\): \(\sqrt{x}\)
- Cube root of a number \(x\): \(\sqrt[3]{x}\)
Steps to Calculate Roots
- Identify the number for which you need to find the root.
- Determine if you are calculating a square root or a cube root.
- Use appropriate mathematical methods or technology tools for accurate computation.
Understanding these concepts and how to calculate roots is crucial for solving a wide range of mathematical problems, from simple equations to more complex algebraic expressions.
What is the Cube Root?
The cube root of a number is the value that, when multiplied by itself three times, gives the original number. It is an essential concept in mathematics, particularly in algebra and geometry. The cube root is represented using the radical symbol with an index of three (∛).
Mathematically, if \( x \) is the cube root of \( y \), then:
\[ x = \sqrt[3]{y} \]
For example, to find the cube root of 27, we solve for \( x \) in the equation:
\[ x^3 = 27 \]
By inspection or calculation, we find that:
\[ 3^3 = 3 \times 3 \times 3 = 27 \]
Therefore, the cube root of 27 is:
\[ \sqrt[3]{27} = 3 \]
Properties of Cube Roots:
- Uniqueness: Every real number has a unique real cube root.
- Negative Numbers: The cube root of a negative number is also negative. For example, \(\sqrt[3]{-8} = -2\).
- Zero: The cube root of zero is zero, \(\sqrt[3]{0} = 0\).
Steps to Calculate the Cube Root:
- Identify the number: Determine the number for which you want to find the cube root.
- Prime Factorization (optional): For some numbers, breaking them down into prime factors can simplify finding the cube root.
- Use a Calculator: For non-perfect cubes, use a scientific calculator or online tool to find an approximate value.
Understanding the cube root is crucial for solving equations involving volume and for applications in various fields such as physics, engineering, and computer science.
What is the Square Root?
The square root of a number is a value that, when multiplied by itself, gives the original number. In other words, for a given number x, the square root is a number y such that \( y^2 = x \).
Mathematically, the square root of x is denoted as \( \sqrt{x} \). For example, \( \sqrt{9} = 3 \) because \( 3^2 = 9 \).
Calculating the Square Root
To calculate the square root of a number, you can use several methods:
- Using a calculator or a computer software that has a square root function.
- Estimating by hand using the long division method.
- Utilizing prime factorization, where you break down the number into its prime factors and then take the square root of each factor pair.
Examples
- \( \sqrt{16} = 4 \) because \( 4^2 = 16 \)
- \( \sqrt{25} = 5 \) because \( 5^2 = 25 \)
- \( \sqrt{36} = 6 \) because \( 6^2 = 36 \)
Properties of Square Roots
Some important properties of square roots include:
- \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
- \( \sqrt{a^2} = |a| \), where \(|a|\) denotes the absolute value of \(a\)
Understanding the Square Root of 27
The square root of 27, denoted as \( \sqrt{27} \), can be simplified by recognizing that 27 is not a perfect square. However, it can be expressed in its simplest radical form:
\( \sqrt{27} = \sqrt{9 \times 3} = \sqrt{9} \times \sqrt{3} = 3\sqrt{3} \)
Therefore, \( \sqrt{27} \) is approximately equal to 5.196 when rounded to three decimal places.
Practice Problem
Calculate the square root of 81. Provide your answer in both exact form and decimal form.
How to Calculate the Cube Root of 27
The cube root of a number is a value that, when multiplied by itself three times, gives the original number. The cube root of 27 can be calculated using the following steps:
Step-by-Step Calculation
-
Prime Factorization:
First, find the prime factors of 27:
27 = 3 × 3 × 3
-
Group the Factors:
Since 27 is a perfect cube, we can group the factors in sets of three:
27 = 33
-
Apply the Cube Root:
Now, take the cube root of both sides:
∛27 = ∛(33)
The cube root of 33 is 3.
Therefore, the cube root of 27 is:
∛27 = 3
Mathematical Notation
- Exponent Form: \( 27^{\frac{1}{3}} \)
- Radical Form: \( \sqrt[3]{27} \)
Example Calculation
To better understand the cube root, consider this example:
- Given a cube with a volume of 27 cubic units, the side length of the cube is the cube root of 27, which is 3 units.
Understanding cube roots helps in solving various mathematical problems and is essential in fields such as physics and engineering.
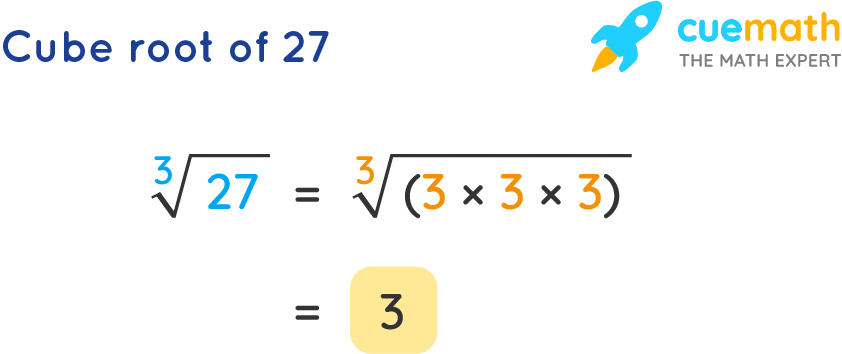
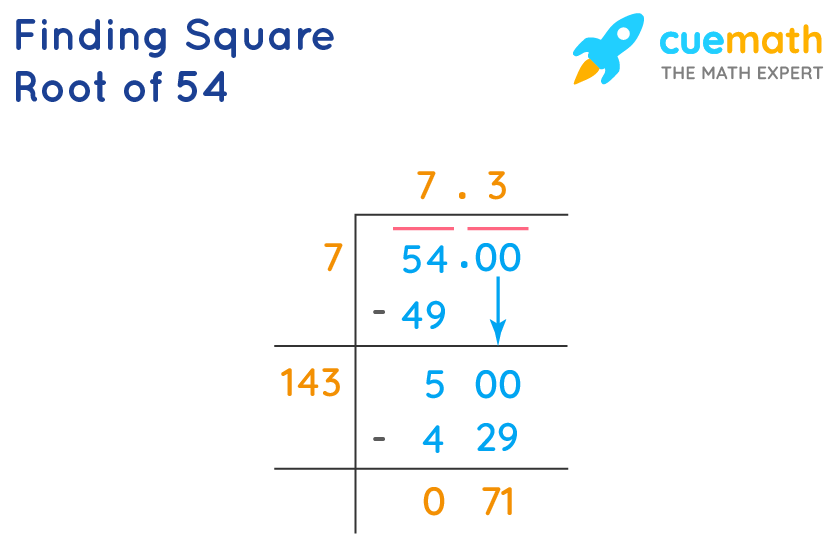
Steps to Find the Square Root of 27
To find the square root of 27, we can follow a step-by-step process. This can include factoring the number, simplifying the radicals, and approximating the value. Here are the steps:
-
Factor the Number: Begin by factoring 27 into its prime factors.
\( 27 = 3^3 \) -
Break Down the Radical: Express the square root of 27 in terms of its prime factors.
\( \sqrt{27} = \sqrt{3^3} \) -
Simplify the Radicals: Use the property of square roots that states
\( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \) to simplify the expression.\( \sqrt{3^3} = \sqrt{3^2 \cdot 3} = \sqrt{3^2} \cdot \sqrt{3} = 3\sqrt{3} \) -
Approximate the Value: To find the decimal approximation, calculate the value of
\( \sqrt{3} \approx 1.732 \) and multiply by 3.\( 3 \cdot 1.732 \approx 5.196 \)
Thus, the simplified form of the square root of 27 is
Properties of Cube Roots
The cube root of a number is a value that, when multiplied by itself three times, gives the original number. Here are some key properties of cube roots:
- Definition: The cube root of a number \( x \) is a number \( y \) such that \( y^3 = x \). It is denoted as \( \sqrt[3]{x} \).
- Perfect Cubes: If a number is a perfect cube, its cube root will be an integer. For example, \( \sqrt[3]{27} = 3 \) because \( 3 \times 3 \times 3 = 27 \).
- Sign Preservation: The cube root of a positive number is positive, and the cube root of a negative number is negative. For instance, \( \sqrt[3]{-27} = -3 \).
- Non-integer Results: If a number is not a perfect cube, its cube root will be an irrational number. For example, \( \sqrt[3]{20} \) is approximately \( 2.727 \).
- Cube of a Cube Root: The cube of the cube root of a number returns the original number, i.e., \( (\sqrt[3]{x})^3 = x \).
Steps to Simplify Cube Roots
- Identify if the number is a perfect cube. If so, the cube root is an integer.
- If the number is not a perfect cube, factorize it to find any perfect cube factors.
- Take the cube root of the perfect cube factors separately.
- Combine the results to get the simplified form.
Example:
Simplify \( \sqrt[3]{54} \)
- 54 is not a perfect cube.
- Factorize 54 into \( 27 \times 2 \) where 27 is a perfect cube.
- \( \sqrt[3]{54} = \sqrt[3]{27 \times 2} = \sqrt[3]{27} \times \sqrt[3]{2} \)
- \( \sqrt[3]{27} = 3 \), so \( \sqrt[3]{54} = 3 \times \sqrt[3]{2} \)
- Thus, \( \sqrt[3]{54} \approx 3 \times 1.2599 \approx 3.7797 \)
Additional Properties:
- Commutative Property: The cube root operation is commutative, meaning \( \sqrt[3]{a \cdot b} = \sqrt[3]{a} \cdot \sqrt[3]{b} \).
- Associative Property: The cube root of a product can be broken down into the product of cube roots, \( \sqrt[3]{a \cdot b \cdot c} = \sqrt[3]{a} \cdot \sqrt[3]{b} \cdot \sqrt[3]{c} \).
- Inverse Property: The cube root function is the inverse of the cube function, so \( \sqrt[3]{(x^3)} = x \).
Properties of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. Understanding the properties of square roots helps in simplifying expressions and solving equations involving square roots. Here are some key properties:
- Non-Negative Results: The square root of a non-negative number is always non-negative. For example, √25 = 5.
- Perfect Squares: If a number is a perfect square, its square root is an integer. For example, √49 = 7 because 49 is 7 squared.
- Product Property: The square root of a product is equal to the product of the square roots of the factors:
\(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\). For example, \(\sqrt{36} = \sqrt{4 \cdot 9} = \sqrt{4} \cdot \sqrt{9} = 2 \cdot 3 = 6\).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots of the numerator and the denominator:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\). For example, \(\sqrt{\frac{25}{9}} = \frac{\sqrt{25}}{\sqrt{9}} = \frac{5}{3}\).
- Non-Perfect Squares: If a number is not a perfect square, its square root is an irrational number. For example, √2 is approximately 1.4142135, and it cannot be expressed as a fraction.
- Even and Odd Perfect Squares: The square root of an even perfect square is always even, and the square root of an odd perfect square is always odd. For example, √144 = 12 (even), and √225 = 15 (odd).
- Negative Numbers: The square root of a negative number is not a real number but an imaginary number. For example, √(-9) = 3i.
By understanding these properties, one can simplify complex square root expressions and solve related mathematical problems more efficiently.
Examples of Cube Roots
Understanding cube roots can be made easier by looking at several examples. Here, we will explore the cube roots of various numbers, starting with the cube root of 27.
- Cube Root of 27: The cube root of 27 is 3. This is because \( 3^3 = 27 \). In mathematical notation: \[ \sqrt[3]{27} = 3 \]
- Cube Root of 8: The cube root of 8 is 2. This is because \( 2^3 = 8 \). In mathematical notation: \[ \sqrt[3]{8} = 2 \]
- Cube Root of 64: The cube root of 64 is 4. This is because \( 4^3 = 64 \). In mathematical notation: \[ \sqrt[3]{64} = 4 \]
- Cube Root of 125: The cube root of 125 is 5. This is because \( 5^3 = 125 \). In mathematical notation: \[ \sqrt[3]{125} = 5 \]
For non-perfect cubes, the cube root can be a more complex number. Here are some examples:
- Cube Root of 2: The cube root of 2 is approximately 1.26, because \( 1.26^3 \approx 2 \).
- Cube Root of 10: The cube root of 10 is approximately 2.15, because \( 2.15^3 \approx 10 \).
- Cube Root of 50: The cube root of 50 is approximately 3.68, because \( 3.68^3 \approx 50 \).
Understanding the cube roots of both perfect and non-perfect cubes helps build a stronger foundation in mathematics.

Examples of Square Roots
Here are some examples of square roots, including the square root of 27:
-
Square Root of 27: \( \sqrt{27} \) can be simplified as follows:
Step 1: Factorize 27 into prime factors: \( 27 = 3 \times 3 \times 3 \). Step 2: Identify pairs of identical factors: \( \sqrt{27} = \sqrt{3^3} \). Step 3: Apply the property of square roots: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). Step 4: Calculate the square root: \( \sqrt{27} = 3\sqrt{3} \). -
Other Examples:
- Square Root of 16: \( \sqrt{16} = 4 \).
- Square Root of 36: \( \sqrt{36} = 6 \).
- Square Root of 64: \( \sqrt{64} = 8 \).
Applications of Cube Roots in Real Life
The cube root of a number is essential in various real-life applications, particularly in fields that involve three-dimensional measurements and analysis. Here are some common and important applications of cube roots:
- Volume Calculation: The cube root is frequently used to determine the side length of a cube when the volume is known. For example, if a cube has a volume of 27 cubic units, its side length is the cube root of 27, which is 3 units.
- Architecture and Engineering: Architects and engineers use cube roots to calculate dimensions and structural properties when designing buildings, bridges, and other structures that require precise volumetric measurements.
- Physics and Engineering: In physics, cube roots are used to determine quantities like density, where volume is a factor. For instance, to find the side length of a cube-shaped object with a given volume to understand its spatial properties.
- Material Science: In material science, the cube root helps in understanding and calculating properties related to the volume of materials. This is crucial when dealing with nanoparticles or other small-scale materials.
- Economics and Finance: Economists use cube roots in certain models to understand growth rates and economic indicators that involve three-dimensional data, such as production and inventory levels.
- Astronomy: Cube roots are used in calculating the size of astronomical objects and their distances. For example, the average density of celestial bodies can be derived from their volume and mass.
- Computer Graphics: In computer graphics and gaming, cube roots are used to calculate scaling factors and to ensure that objects maintain their proportions when resized in three-dimensional space.
- Hydraulics and Fluid Dynamics: Engineers use cube roots to calculate the capacity of tanks and reservoirs, ensuring efficient storage and flow of liquids.
By understanding and applying cube roots, we can solve complex problems and make accurate predictions in various scientific, engineering, and practical contexts. Mastery of cube roots enhances our ability to work with three-dimensional data effectively.
Applications of Square Roots in Real Life
The square root of a number is a fundamental mathematical concept that has numerous practical applications in various fields. Here are some key real-life applications of square roots:
- Geometry and Construction: Square roots are used to calculate the dimensions of a square when the area is known. For example, if a square has an area of 27 square units, its side length is the square root of 27, which is approximately \( \sqrt{27} \approx 5.2 \) units.
- Physics and Engineering: In physics, square roots are essential in calculating quantities such as the root mean square (RMS) value of an alternating current (AC) voltage or current. RMS is used to determine the effective value of the fluctuating electrical quantities.
- Statistics: Square roots are used in the calculation of standard deviation, a measure of the dispersion of a set of data points. The standard deviation is the square root of the variance and provides insights into the variability within a dataset.
- Finance and Economics: In finance, square roots are used in risk assessment models, such as calculating the volatility of stock prices. The standard deviation, which involves the square root, helps in understanding the risk and return of investments.
- Computer Science: In computer algorithms, square roots are used in various search algorithms and optimizations. For instance, the Euclidean distance between two points in a plane involves the square root function.
- Medicine: Square roots are used in medical calculations, such as determining the body surface area (BSA) for dosing medications. BSA is calculated using the square root of the product of height and weight.
- Astronomy: Astronomers use square roots to calculate distances and magnitudes. For example, the inverse square law of light involves the square root when determining how the intensity of light diminishes with distance.
- Acoustics: In acoustics, the intensity of sound is often related to the square root of its power. This relationship helps in understanding sound levels and designing acoustically efficient spaces.
- Agriculture: Farmers use square roots to calculate the area of land plots, which is essential for planting, irrigation, and managing resources effectively.
By understanding and applying square roots, we can solve practical problems, make informed decisions, and understand the world around us better. Mastery of square roots is crucial for success in many scientific, engineering, and everyday contexts.
Common Mistakes in Calculating Roots
Calculating square and cube roots can often lead to errors if certain common mistakes are not avoided. Here are some frequent mistakes and tips to prevent them:
- Ignoring the Order of Operations: Always remember to follow the correct order of operations (PEMDAS/BODMAS). For example, when calculating \(3\sqrt{27}\), ensure you find the square root first before multiplying.
- Incorrect Square Root Simplification: Ensure you correctly simplify the square root. For example, \(\sqrt{27}\) should be simplified to \(3\sqrt{3}\) since \(27 = 3^3\).
- Misapplying Properties of Roots: The square root of a product is the product of the square roots, but this is often misapplied. For example, \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\), but only if \(a\) and \(b\) are non-negative.
- Forgetting to Simplify Completely: After performing initial operations, always check if the expression can be further simplified. For instance, after calculating \(\sqrt{27} = 3\sqrt{3}\), check if the coefficients can be simplified.
- Overlooking Prime Factorization: Prime factorization is crucial for simplifying roots. For example, recognizing that \(27 = 3^3\) helps in simplifying \(\sqrt{27}\) correctly.
Here are steps to correctly calculate and simplify the square root of 27:
- Factorize the number under the square root: \(27 = 3 \times 3 \times 3\).
- Group the factors into pairs: \(27 = (3 \times 3) \times 3 = 9 \times 3\).
- Take the square root of each pair: \(\sqrt{9 \times 3} = \sqrt{9} \times \sqrt{3}\).
- Simplify the roots: \(\sqrt{9} = 3\), hence \(\sqrt{27} = 3\sqrt{3}\).
By following these steps and avoiding common mistakes, you can accurately calculate roots and understand the mathematical principles behind them.
Common errors also occur with calculators. Here are tips to avoid these issues:
- Misinterpreting Calculator Outputs: Ensure you understand error messages and double-check your input.
- Incorrect Data Entry: Carefully enter numbers to avoid typos that lead to incorrect results.
By being mindful of these common mistakes and following proper calculation steps, you can achieve accurate and reliable results when working with roots.

Understanding the Relationship Between Cubes and Cube Roots
The relationship between cubes and cube roots is fundamental in mathematics. Here, we explore how these concepts are interconnected and how to effectively understand and compute them.
To begin with, a cube of a number is found by multiplying the number by itself three times. Mathematically, if a is a number, then its cube is represented as:
= a × a × a
For example:
- 2 cubed is 8, because 2 × 2 × 2 = 8.
- 3 cubed is 27, because 3 × 3 × 3 = 27.
Conversely, the cube root of a number is the value that, when cubed, gives the original number. The cube root is denoted by the radical symbol with a small three:
= b if b³ = a
For instance:
- The cube root of 8 is 2, since 2³ = 8.
- The cube root of 27 is 3, since 3³ = 27.
Steps to Compute Cube Roots
- Identify the number you want to find the cube root of.
- Determine the factors of the number to see if it is a perfect cube.
- Use the prime factorization method to break down the number into its prime factors.
- Group the prime factors into triples. If each group multiplies to the same number, that number is the cube root.
Let's consider an example:
To find the cube root of 64:
- Prime factorize 64: 64 = 2 × 2 × 2 × 2 × 2 × 2 = 2³ × 2³.
- Group the factors into triples: (2³) × (2³).
- Since the triples multiply to the same number, the cube root of 64 is 4.
Another example is finding the cube root of 27:
- Prime factorize 27: 27 = 3 × 3 × 3 = 3³.
- Since 27 is already a perfect cube, its cube root is 3.
Properties of Cubes and Cube Roots
- Cube of a Negative Number: The cube of a negative number is also negative. For example, (-3)³ = -27.
- Cube Root of a Negative Number: The cube root of a negative number is also negative. For example, ∛(-27) = -3.
- Inverse Relationship: Cubing a number and taking the cube root are inverse operations. If a³ = b, then ∛b = a.
Understanding the relationship between cubes and cube roots helps in simplifying complex mathematical problems and finding solutions more efficiently. Mastery of these concepts is essential for advanced mathematics and various real-world applications.
Understanding the Relationship Between Squares and Square Roots
Understanding the relationship between squares and square roots is fundamental in mathematics. Squaring a number and finding the square root of a number are inverse operations, meaning that one operation reverses the effect of the other.
When you square a number, you multiply it by itself:
\(a^2 = a \times a\)
For example, \(5^2 = 5 \times 5 = 25\).
To find the square root of a number, you determine what number, when squared, gives the original number:
\(\sqrt{a^2} = a\)
For example, \(\sqrt{25} = 5\).
The relationship can be summarized as follows:
- Squaring a number is the process of multiplying it by itself.
- Finding the square root of a number is the process of determining which number squared results in the original number.
Here are some key points to consider:
- The square of a number is always non-negative.
- The square root of a positive number is always positive.
- The square root of zero is zero.
- Negative numbers do not have real square roots because the square of any real number is non-negative.
In mathematical notation:
If \(x^2 = y\), then \(x = \pm\sqrt{y}\).
This means that both positive and negative numbers can be square roots of a given positive number.
Let's look at some examples:
| Number (n) | Square (n^2) | Square Root (\(\sqrt{n^2}\)) |
|---|---|---|
| 3 | 9 | 3 |
| 4 | 16 | 4 |
| 5 | 25 | 5 |
Understanding this relationship is crucial for solving quadratic equations, understanding geometric concepts, and performing various calculations in algebra and beyond.
For instance, in solving the equation \(x^2 = 27\), we find:
\(x = \pm\sqrt{27} \approx \pm 5.196\)
Thus, the concepts of squares and square roots are deeply interrelated, forming a fundamental part of mathematical learning and application.
Mathematical Notation and Symbols for Roots
In mathematics, roots are fundamental operations used to solve equations and understand relationships between numbers. Below are some key notations and symbols used for representing roots:
Square Root
The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). It is denoted by the radical symbol \( \sqrt{} \).
- The principal square root of \( x \) is written as \( \sqrt{x} \).
- The principal square root of 27 is written as \( \sqrt{27} \).
- For example, \( \sqrt{9} = 3 \) because \( 3^2 = 9 \).
Cube Root
The cube root of a number \( x \) is a value that, when multiplied by itself three times, gives \( x \). It is denoted by the radical symbol with an index of 3: \( \sqrt[3]{} \).
- The cube root of \( x \) is written as \( \sqrt[3]{x} \).
- The cube root of 27 is written as \( \sqrt[3]{27} \).
- For example, \( \sqrt[3]{27} = 3 \) because \( 3^3 = 27 \).
General n-th Root
The n-th root of a number \( x \) is a value that, when raised to the power of \( n \), gives \( x \). It is denoted by the radical symbol with an index of \( n \): \( \sqrt[n]{} \).
- The n-th root of \( x \) is written as \( \sqrt[n]{x} \).
- For example, the 4th root of 16 is \( \sqrt[4]{16} = 2 \) because \( 2^4 = 16 \).
Radicand
The radicand is the number or expression inside the radical symbol. For example, in \( \sqrt{27} \), the number 27 is the radicand.
Properties of Roots
- \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\) - The square root of a product is the product of the square roots.
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) - The square root of a quotient is the quotient of the square roots.
- \(\sqrt[n]{a^m} = a^{\frac{m}{n}}\) - The n-th root of \( a^m \) can be written as \( a \) raised to the power of \( \frac{m}{n} \).
Special Notations
- \(\pm \sqrt{x}\) - Represents both the positive and negative square roots of \( x \).
- For example, \( \pm \sqrt{16} = \pm 4 \) because both 4 and -4 are square roots of 16.
Understanding these notations and properties is crucial for solving various mathematical problems involving roots. Proper use of these symbols helps in communicating mathematical ideas clearly and effectively.
Using Technology to Calculate Roots
In today's digital age, technology provides us with various tools and methods to easily calculate roots. These tools range from basic calculators to sophisticated computer software and online platforms. Below are some key ways technology can assist in calculating roots:
-
Scientific Calculators:
Most scientific calculators have built-in functions for calculating square roots and cube roots. To find a square root, you typically use the √ button. For cube roots, some calculators have a specific button, or you may need to use the general root function and specify the degree.
-
Graphing Calculators:
Graphing calculators not only compute roots but also graph the functions to visualize the solutions. These calculators are especially useful in educational settings for understanding the behavior of root functions.
-
Online Calculators:
Websites like Mathway and Calculator.dev offer online tools for calculating roots. These tools are accessible from any device with internet access and provide step-by-step solutions to root problems, making them great for learning and verification purposes.
-
Mathematical Software:
Software like MATLAB, Mathematica, and Python libraries (e.g., NumPy) allow for advanced root calculations, including symbolic computation and numerical analysis. These tools are essential for higher-level mathematics and engineering applications.
-
Mobile Apps:
Many mobile apps are available for root calculations, providing convenience and accessibility on the go. These apps often include additional features like unit converters and equation solvers.
Steps to Use Technology for Root Calculations
- Choose your preferred tool: calculator, online platform, software, or mobile app.
- Input the number you want to find the root of.
- Select the type of root calculation (square root, cube root, etc.).
- Follow the tool's instructions to compute the root.
- Review the result and, if necessary, explore step-by-step solutions or visualizations provided by the tool.
Using technology to calculate roots not only simplifies the process but also enhances understanding through interactive and visual aids. Whether you are a student, educator, or professional, these tools can significantly improve your efficiency and accuracy in solving root-related problems.

Practice Problems for Cube Roots
Here are some practice problems to help you understand and master cube roots:
-
Find the cube root of 27.
Solution: \(\sqrt[3]{27} = 3\)
-
Calculate the cube root of 64.
Solution: \(\sqrt[3]{64} = 4\)
-
Determine the cube root of 125.
Solution: \(\sqrt[3]{125} = 5\)
-
What is the cube root of 216?
Solution: \(\sqrt[3]{216} = 6\)
-
Find the cube root of 1000.
Solution: \(\sqrt[3]{1000} = 10\)
Here are some more challenging problems:
-
Find the cube root of 729.
Solution: \(\sqrt[3]{729} = 9\)
-
Calculate the cube root of 1331.
Solution: \(\sqrt[3]{1331} = 11\)
-
Determine the cube root of 1728.
Solution: \(\sqrt[3]{1728} = 12\)
-
What is the cube root of 2744?
Solution: \(\sqrt[3]{2744} = 14\)
-
Find the cube root of 3375.
Solution: \(\sqrt[3]{3375} = 15\)
Now, try solving these word problems:
-
A cube has a volume of 343 cubic units. What is the length of one side of the cube?
Solution: The side length is \(\sqrt[3]{343} = 7\) units.
-
If the volume of a cube is 512 cubic centimeters, what is the length of each edge?
Solution: The edge length is \(\sqrt[3]{512} = 8\) centimeters.
-
A storage box in the shape of a cube has a volume of 27 cubic feet. What is the length of one side of the box?
Solution: The side length is \(\sqrt[3]{27} = 3\) feet.
-
The volume of a cubical container is 1331 cubic inches. Find the length of one side.
Solution: The side length is \(\sqrt[3]{1331} = 11\) inches.
-
A die has a volume of 216 cubic millimeters. What is the side length of the die?
Solution: The side length is \(\sqrt[3]{216} = 6\) millimeters.
Practice Problems for Square Roots
Here are some practice problems to help you understand and master the concept of square roots:
-
Find the square root of 49.
Solution: \(\sqrt{49} = 7\)
-
Calculate the square root of 81.
Solution: \(\sqrt{81} = 9\)
-
Determine the square root of 144.
Solution: \(\sqrt{144} = 12\)
-
What is the square root of 16?
Solution: \(\sqrt{16} = 4\)
-
Find the square root of 225 using the prime factorization method.
Solution:
- Prime factors of 225: \(225 = 3^2 \times 5^2\)
- Square root: \(\sqrt{225} = 3 \times 5 = 15\)
Calculate the square root of 121 by estimation.
Solution:
- Find nearest perfect squares: \(100\) and \(144\)
- Estimate: \(\sqrt{121} \approx 11\)
What is the square root of 200 using the long division method?
Solution:
- Pair digits: \(20|00\)
- Find the largest number whose square is less than or equal to 20: \(4\)
- Long division steps to refine: Result is approximately \(14.14\)
Find the square root of 18 to the nearest tenth.
Solution: \(\sqrt{18} \approx 4.2\)
-
Calculate the square root of 0.25.
Solution: \(\sqrt{0.25} = 0.5\)
-
What is the square root of 2? Provide an approximate value.
Solution: \(\sqrt{2} \approx 1.414\)
These problems cover various methods to calculate square roots, including prime factorization, estimation, and the long division method, ensuring a comprehensive understanding of the topic.
Xem video để học cách tìm căn bậc ba của 8 và 27 một cách dễ dàng và không cần dùng máy tính.
Tìm căn bậc ba của 8 và 27 mà không cần máy tính
READ MORE:
Xem video để hiểu rõ cách tính căn bậc ba của 27 một cách chi tiết và dễ hiểu.
Giải thích Căn bậc ba của 27