Topic 3 square root 64: The concept of the square root is fundamental in mathematics, and understanding it can open the door to a deeper appreciation of mathematical principles. This article delves into the 3 square root of 64, exploring its significance, methods to calculate it, and its applications in various fields. Join us in uncovering the mysteries of mathematical roots!
Table of Content
- Search Results for "3 square root 64"
- Introduction to Square Roots
- Definition and Basic Properties of Square Roots
- Calculating the Square Root of 64
- Methods to Find Square Roots
- Applications of Square Roots in Real Life
- The Importance of 64 in Mathematics
- Exploring Cube Roots
- Mathematical Patterns Involving 64
- Practice Problems and Exercises
- Conclusion and Summary
- YOUTUBE: Tìm hiểu cách tính căn bậc ba của 64 mà không cần sử dụng máy tính. Video hướng dẫn chi tiết và dễ hiểu.
Search Results for "3 square root 64"
The square root of a number is a value that, when multiplied by itself, gives the original number. For the expression "3 square root 64," the result is:
$\sqrt[3]{64} = 4$
This means that the cube root of 64 is 4. In other words, 4 multiplied by itself three times equals 64.
READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical notation, the square root of a number x is written as \(\sqrt{x}\). The square root symbol is also called a radical, and the number under the radical sign is called the radicand.
Square roots are fundamental in mathematics and have various applications in different fields such as geometry, algebra, and calculus. They are particularly important in solving quadratic equations and in understanding the properties of numbers and shapes.
For example, the square root of 64 is 8, because \(8 \times 8 = 64\). This can be written as:
\(\sqrt{64} = 8\)
There are several key properties of square roots that are useful to know:
- Non-negative Numbers: The square root of a non-negative number is always non-negative.
- Product Property: The square root of a product is equal to the product of the square roots, i.e., \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).
- Quotient Property: The square root of a quotient is equal to the quotient of the square roots, i.e., \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\), where \(b \ne 0\).
- Squares of Square Roots: The square of the square root of a number returns the original number, i.e., \((\sqrt{a})^2 = a\).
In addition to these properties, it's important to note that not all numbers have integer square roots. For instance, the square root of 2 is an irrational number, which means it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating.
Understanding square roots also involves recognizing perfect squares, which are numbers that have integer square roots. Some common perfect squares include 1, 4, 9, 16, 25, 36, 49, and 64. These numbers are important in various mathematical contexts and often serve as benchmarks for learning and calculations.
In the following sections, we will delve deeper into the definition and properties of square roots, methods to calculate them, and their applications in real life. We will also explore the significance of the number 64 in mathematics, including its role as a perfect square and its place in the powers of 2.
Definition and Basic Properties of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical terms, if \( x \) is the square root of \( y \), then \( x^2 = y \).
The square root of 64 is denoted as \( \sqrt{64} \), and since \( 8 \times 8 = 64 \), we have:
\[
\sqrt{64} = 8
\]
Some basic properties of square roots include:
- Non-negative result: The square root of a non-negative number is always non-negative. For example, \( \sqrt{64} = 8 \), and not -8.
- Product property: The square root of a product is the product of the square roots of the factors. Mathematically, \[ \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \]. For example, \[ \sqrt{64 \times 16} = \sqrt{64} \times \sqrt{16} = 8 \times 4 = 32 \].
- Quotient property: The square root of a quotient is the quotient of the square roots of the numerator and the denominator. Mathematically, \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]. For example, \[ \sqrt{\frac{64}{16}} = \frac{\sqrt{64}}{\sqrt{16}} = \frac{8}{4} = 2 \].
Square roots have significant applications in various fields such as geometry, algebra, and calculus. Understanding the properties of square roots is fundamental to solving many mathematical problems.
Calculating the Square Root of 64
Calculating the square root of 64 is straightforward, as 64 is a perfect square. Here, we will outline different methods to find the square root of 64:
- Prime Factorization Method:
- Find the prime factors of 64. The factorization of 64 is:
\[ 64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^6 \]
- Group the prime factors into pairs of identical numbers:
\[ (2 \times 2) \times (2 \times 2) \times (2 \times 2) = 8 \]
- Take one number from each pair and multiply them:
\[ \sqrt{64} = 2 \times 2 \times 2 = 8 \]
- Direct Calculation Method:
- Verification:
Recognize that 64 is a perfect square. By definition, the square root of a perfect square is an integer.
\[ \sqrt{64} = 8 \]
We can verify our result by squaring the obtained square root:
\[ 8^2 = 64 \]
This confirms that the square root of 64 is indeed 8.
Additionally, the concept of a square root can be extended to understand other mathematical operations and real-life applications.
For instance, if you have a square with an area of 64 square units, each side of the square will measure 8 units. Similarly, if a circle has an area of 64π square units, its radius would be 8 units since:
\[ \pi r^2 = 64\pi \]
\[ r^2 = 64 \]
\[ r = \sqrt{64} = 8 \]
In conclusion, the square root of 64 is an essential mathematical concept that can be calculated using various methods and has multiple applications in different fields.
Methods to Find Square Roots
Finding square roots is a fundamental mathematical skill that can be approached using several methods. Below, we outline two popular methods for finding square roots: the Prime Factorization Method and the Long Division Method.
Prime Factorization Method
The Prime Factorization Method involves breaking down the number into its prime factors and then pairing the prime factors to find the square root. Here are the steps to find the square root of 64 using this method:
- First, express 64 as a product of prime numbers: \(64 = 2 \times 2 \times 2 \times 2 \times 2 \times 2\).
- Group the prime factors into pairs: \( (2 \times 2) \times (2 \times 2) \times (2 \times 2) \).
- Take one number from each pair: \( 2 \times 2 \times 2 \).
- Multiply these numbers together to get the square root: \( 2 \times 2 \times 2 = 8 \).
Therefore, the square root of 64 is 8.
Long Division Method
The Long Division Method is a more systematic approach to finding square roots, especially for larger numbers. Here are the steps to find the square root of 64 using this method:
- Start by pairing the digits of the number from right to left. For 64, we have one pair: (64).
- Find the largest number whose square is less than or equal to the first pair. Here, 8 is the largest number because \(8^2 = 64\).
- Write 8 as the quotient. Since \(8 \times 8 = 64\), subtract 64 from 64 to get a remainder of 0.
Since there are no more pairs of digits to bring down and the remainder is 0, the square root of 64 is 8.
Below is a representation of the long division method:
| 8 | |
| 64 | 8 |
| 64 | |
| 0 |
Using these methods, we can effectively determine the square root of 64. Both methods are useful depending on the context and the number involved.
Applications of Square Roots in Real Life
Square roots have numerous applications in various fields. Here are some key examples:
Geometry and Area Calculations
Square roots are commonly used in geometry to determine the side length of a square when its area is known. For instance, if the area of a square is 64 square units, the length of each side is calculated as follows:
\[
\sqrt{64} = 8 \text{ units}
\]
This principle is useful in real-life situations, such as determining the dimensions of a plot of land or a piece of fabric when only the area is provided.
Physics and Engineering
Square roots are also crucial in physics, especially in kinematic equations involving gravity. For example, the time \( t \) it takes for an object to fall from a height \( h \) is given by:
\[
t = \frac{\sqrt{h}}{4}
\]
For an object dropped from a height of 64 feet, the time to reach the ground is:
\[
t = \frac{\sqrt{64}}{4} = 2 \text{ seconds}
\]
Accident Investigations
In accident investigations, police officers use the length of skid marks to estimate the speed of a vehicle before the brakes were applied. If \( d \) is the length of the skid marks, the speed \( s \) can be calculated as:
\[
s = \sqrt{24d}
\]
For skid marks of 190 feet, the speed is approximately:
\[
s = \sqrt{24 \times 190} \approx 67.5 \text{ mph}
\]
Distance Calculations
Square roots are used to calculate distances between points in both 2D and 3D space. The distance \( D \) between points \((x_1, y_1)\) and \((x_2, y_2)\) is given by:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
This formula is derived from the Pythagorean theorem and is used in various fields, including navigation, architecture, and computer graphics.
Quadratic Equations
Square roots are essential in solving quadratic equations using the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
This formula is used in many areas of science and engineering to find the roots of quadratic equations, which often represent critical points in a system or process.
Construction and Design
In construction, square roots help determine dimensions for various projects. For example, if a square patio has an area of 200 square feet, the length of each side is:
\[
\sqrt{200} \approx 14.1 \text{ feet}
\]
These examples illustrate how square roots play a vital role in practical applications, making them an essential mathematical concept in everyday life.
The Importance of 64 in Mathematics
The number 64 holds significant importance in mathematics due to its unique properties and its role in various mathematical concepts.
64 as a Perfect Square
64 is a perfect square because it can be expressed as the product of an integer with itself. Mathematically, this is shown as:
\[ 64 = 8 \times 8 = 8^2 \]
Being a perfect square, 64 has several implications in mathematics:
- It simplifies calculations in geometry, especially when dealing with areas and squares.
- In algebra, it aids in solving quadratic equations where the solutions involve square roots of perfect squares.
Role of 64 in Powers of 2
64 is a power of 2, specifically:
\[ 64 = 2^6 \]
This property makes it integral in fields like computer science, where binary systems and power of two calculations are fundamental. Key aspects include:
- Binary Representation: In binary, 64 is represented as \(1000000_2\), making it a milestone in digital computing.
- Memory and Storage: Computer memory and storage are often organized in powers of two, making 64 GB a common capacity.
Mathematical Patterns Involving 64
64 exhibits interesting patterns in mathematics. For instance:
- It is both a perfect square and a perfect cube:
- Perfect square: \[ 64 = 8^2 \]
- Perfect cube: \[ 64 = 4^3 \]
These properties illustrate the versatility of 64 in different mathematical contexts.
Applications of 64 in Real-Life Mathematics
The number 64 is not just theoretical but has practical applications:
- Geometry and Area Calculations: Knowing the square root of 64 helps in calculating dimensions in construction and design.
- Physics and Engineering: 64 is used in various formulae and calculations, making it vital in these fields.
Practice Problems Involving 64
To understand the significance of 64, practicing problems involving this number can be helpful:
- Find the square root of 64 using different methods (prime factorization, long division).
- Calculate the cube root of 64 and discuss its properties.
- Explore patterns by finding powers and roots of 64 in various equations.
Conclusion
The number 64, being both a perfect square and a perfect cube, plays a crucial role in mathematics and its applications. Understanding its properties helps in various areas of study and practical applications.
Exploring Cube Roots
Definition and Properties of Cube Roots
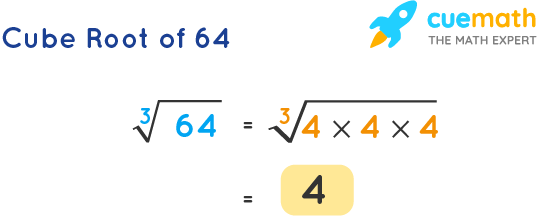
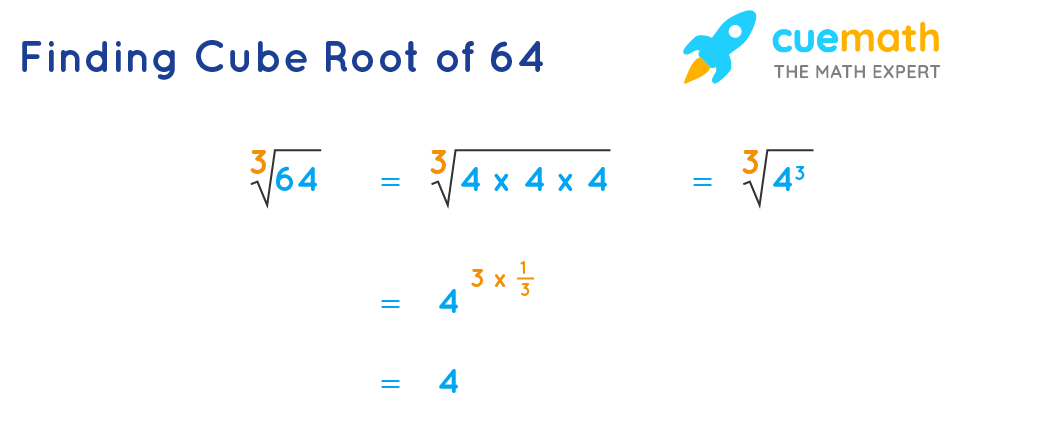
The cube root of a number is a value that, when multiplied by itself three times, gives the original number. It is denoted as \( \sqrt[3]{x} \) or \( x^{1/3} \). For example, \( \sqrt[3]{64} = 4 \) because \( 4^3 = 64 \).
Some properties of cube roots include:
- The cube root of a positive number is positive.
- The cube root of a negative number is negative.
- Cube roots are used to reverse the process of cubing a number.
Calculating the Cube Root of 64
To find the cube root of 64, you need to determine which number multiplied by itself three times equals 64:
\[
\sqrt[3]{64} = 4 \text{ because } 4 \times 4 \times 4 = 64
\]
Therefore, \( \sqrt[3]{64} = 4 \).
How to Calculate Cube Roots Manually
There are several methods to manually calculate cube roots, including:
- Prime Factorization Method: Break down the number into its prime factors and group them into sets of three.
- Estimation Method: Use known cube roots and interpolate between them to estimate the cube root of a given number.
- Using a Calculator: Modern calculators have a cube root function, often represented as \( \sqrt[3]{x} \) or \( x^{1/3} \).
Applications of Cube Roots
Cube roots are essential in various fields, including:
- Geometry: Calculating the side length of a cube given its volume.
- Physics: Determining the properties of objects with cubic relationships, such as density and volume.
- Engineering: Solving problems related to cubic structures and materials.
For instance, if you know the volume of a cube is 64 cubic units, you can find the side length by calculating the cube root of 64, which is 4 units.
Examples and Practice Problems
Here are some examples to help solidify your understanding of cube roots:
- The cube root of 8 is \( \sqrt[3]{8} = 2 \).
- The cube root of 27 is \( \sqrt[3]{27} = 3 \).
- The cube root of 125 is \( \sqrt[3]{125} = 5 \).
Practice problems:
- Find the cube root of 216.
- Calculate \( \sqrt[3]{1000} \).
- Determine the cube root of -27.
Conclusion
Understanding cube roots is crucial for solving mathematical problems involving volume and scaling. Mastering both manual and calculator methods for finding cube roots will enhance your problem-solving skills in various scientific and engineering contexts.
Mathematical Patterns Involving 64
The number 64 plays a significant role in various mathematical patterns and sequences. Here, we explore some of the key patterns and properties associated with 64.
Arithmetic Patterns
In arithmetic sequences, each term is derived by adding a fixed number to the previous term. For example:
- Sequence: 8, 16, 24, 32, 40, 48, 56, 64
- Pattern: Add 8 to each term to get the next term.
Geometric Patterns
In geometric sequences, each term is derived by multiplying the previous term by a fixed number. For instance:
- Sequence: 1, 2, 4, 8, 16, 32, 64
- Pattern: Multiply each term by 2 to get the next term.
Power of 2
64 is a power of 2, specifically \(2^6\). Powers of 2 are fundamental in binary systems and digital computing:
- Exponential Form: \(64 = 2^6\)
- Binary Representation: 64 in binary is 1000000.
Perfect Square
64 is a perfect square, meaning it is the square of an integer:
- Square Root: \( \sqrt{64} = 8 \)
- Property: A perfect square has an integer as its square root.
Perfect Cube
64 is also a perfect cube, meaning it is the cube of an integer:
- Cube Root: \( \sqrt[3]{64} = 4 \)
- Property: A perfect cube has an integer as its cube root.
Fibonacci Sequence
Although 64 itself is not a Fibonacci number, it can be related to Fibonacci sequences in various ways. For example:
- Modified Fibonacci Sequence: Consider the sequence where each term is the sum of the two preceding terms plus a fixed number. For instance, starting with 1 and 2 and adding 1 each time: 1, 2, 4, 7, 12, 20, 33, 54, 88.
Applications in Geometry
64 is significant in geometry, particularly in area calculations:
- Square Area: A square with a side length of 8 units has an area of 64 square units.
- Volume Calculation: A cube with a side length of 4 units has a volume of 64 cubic units.
These patterns and properties illustrate the importance of the number 64 in various mathematical contexts, showcasing its versatility and relevance across different areas of mathematics.
Practice Problems and Exercises
Practicing square roots and cube roots is essential for mastering these concepts. Below are a variety of problems and exercises to help reinforce your understanding.
Square Roots
Find the square root of the following perfect squares:
- √64
- √81
- √144
- √225
- √400
Simplify the square root of the following non-perfect squares to the simplest radical form:
- √50
- √72
- √98
- √128
- √200
Cube Roots
Find the cube root of the following perfect cubes:
- ∛64
- ∛125
- ∛216
- ∛343
- ∛512
Simplify the cube root of the following non-perfect cubes:
- ∛54
- ∛128
- ∛250
- ∛405
- ∛686
Mixed Problems
Solve the following equations involving square roots and cube roots:
- √(x + 9) = 7
- ∛(2x - 16) = 4
- √(x² + 16) = 10
- ∛(3x + 5) = 3
- √(4x + 1) = 5
Real-Life Applications
Apply your knowledge of square roots and cube roots to solve these real-life problems:
- A square garden has an area of 64 square meters. What is the length of one side of the garden?
- A cube-shaped water tank has a volume of 512 cubic meters. What is the length of one edge of the tank?
- If the side length of a square is doubled, by what factor does the area increase?
- The volume of a cube is 343 cubic centimeters. If each edge of the cube is increased by 1 centimeter, what is the new volume?
- A rectangular prism has a volume of 1000 cubic meters. If the height is 10 meters and the width is 10 meters, what is the length?
By practicing these problems, you can solidify your understanding of square roots and cube roots, and how they are used in various mathematical and real-life contexts.
Conclusion and Summary
In this article, we explored the mathematical significance and applications of the square root of 64. Understanding the concept of square roots is fundamental in various fields, including geometry, algebra, and calculus. We began by defining square roots and their properties, emphasizing the importance of 64 as a perfect square.
We delved into the methods to calculate square roots, including prime factorization and long division, and highlighted the principal square root of 64 as 8. Additionally, we explored the broader implications and applications of square roots in real life, such as in geometry for area calculations and in physics and engineering for solving complex equations.
The importance of the number 64 extends beyond its role as a perfect square. It is also significant in powers of 2, playing a crucial role in computer science and digital systems. Moreover, we examined cube roots, specifically the cube root of 64, which is 4, and discussed the properties and calculations involved.
In the section on mathematical patterns involving 64, we observed its occurrence in various sequences and its relevance in different mathematical contexts. To reinforce learning, practice problems and exercises were provided, allowing readers to apply their knowledge and gain proficiency in calculating square roots and understanding their applications.
In summary, mastering the concept of square roots and their applications is essential for advancing in mathematics and related disciplines. The number 64, with its unique properties, serves as a valuable example to illustrate these concepts. By understanding and applying these principles, one can solve a wide range of mathematical problems and appreciate the beauty and utility of mathematics in everyday life.
Tìm hiểu cách tính căn bậc ba của 64 mà không cần sử dụng máy tính. Video hướng dẫn chi tiết và dễ hiểu.
Căn bậc ba của 64 mà không cần máy tính
READ MORE:
Hướng dẫn cách sử dụng phân tích số nguyên tố để tính căn bậc ba của 64. Video chi tiết và dễ hiểu.
Sử dụng phân tích số nguyên tố để tính căn bậc ba của một số, căn bậc ba của 64