Topic 3 square root 27: Discover the simplicity of calculating 3 square root 27 with our comprehensive guide. Learn the basics of square roots, the step-by-step process of simplification, and real-life applications. This article will help you master this mathematical concept effortlessly and accurately. Dive in to enhance your understanding and boost your confidence in solving square root problems.
Table of Content
- Calculating \( \sqrt[3]{27} \)
- Introduction to Square Roots
- Basic Concepts of Square Roots
- Definition of the Square Root of a Number
- Mathematical Explanation of 3 Square Root 27
- Calculating the Square Root of 27
- Simplifying Square Root Expressions
- Step-by-Step Calculation of 3 Square Root 27
- Applications of Square Roots in Real Life
- Importance of Understanding Square Roots
- Common Mistakes in Calculating Square Roots
- Advanced Square Root Problems
- Practice Problems and Solutions
- Conclusion
- Further Reading and Resources
- YOUTUBE: Hướng dẫn tìm căn bậc ba của số 8 và 27 mà không cần dùng máy tính, phù hợp cho học sinh và người yêu thích toán học.
Calculating \( \sqrt[3]{27} \)
The cube root of 27, denoted as \( \sqrt[3]{27} \), can be computed as follows:
| Step 1: | Identify the number whose cube equals 27: |
| Step 2: | Determine the cube root of 27: |
| Step 3: | The cube root of 27 is 3, as \( 3^3 = 27 \). |
![Calculating \( \sqrt[3]{27} \)](https://i.ytimg.com/vi/-dGhlLR6-4Y/maxresdefault.jpg)
READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, often introduced in middle school. The square root of a number \( x \) is a value that, when multiplied by itself, gives the number \( x \). Mathematically, this is expressed as:
\[ \sqrt{x} = y \quad \text{if and only if} \quad y^2 = x \]
For example, the square root of 25 is 5, because \( 5 \times 5 = 25 \).
Square roots can be represented in several ways:
- As a radical symbol: \( \sqrt{x} \)
- As an exponent: \( x^{1/2} \)
Here are some key properties of square roots:
- The square root of a positive number is always positive.
- The square root of 0 is 0.
- Negative numbers do not have real square roots.
In this guide, we will explore how to simplify and calculate square roots, using the example of \( 3 \sqrt{27} \) to illustrate the process. Simplifying square roots often involves breaking down the number inside the radical into its prime factors.
Let's break down \( \sqrt{27} \):
\[ 27 = 3 \times 3 \times 3 = 3^3 \]
Thus,
\[ \sqrt{27} = \sqrt{3^3} = 3 \sqrt{3} \]
Multiplying this by 3, we get:
\[ 3 \sqrt{27} = 3 \times 3 \sqrt{3} = 9 \sqrt{3} \]
Understanding these steps will help you simplify and solve square root problems more efficiently.
Basic Concepts of Square Roots
Understanding square roots is crucial for many areas of mathematics. The square root of a number \( x \) is a value \( y \) such that:
\[ y^2 = x \]
This means \( y \) multiplied by itself equals \( x \). For example:
- \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \)
- \( \sqrt{9} = 3 \) because \( 3 \times 3 = 9 \)
Here are some basic concepts and properties of square roots:
- Positive Results: The principal square root (denoted \( \sqrt{x} \)) of a positive number is always positive. For instance, \( \sqrt{25} = 5 \).
- Zero: The square root of zero is zero. \( \sqrt{0} = 0 \).
- Non-Real Numbers: The square root of a negative number is not a real number. It is an imaginary number. For example, \( \sqrt{-1} = i \), where \( i \) is the imaginary unit.
Square roots can be simplified by expressing the number inside the radical as a product of prime factors. For example:
\[ \sqrt{36} = \sqrt{6 \times 6} = 6 \]
Let's take a detailed look at simplifying \( \sqrt{27} \):
\[ 27 = 3 \times 3 \times 3 = 3^3 \]
Thus, we can write:
\[ \sqrt{27} = \sqrt{3^3} = 3 \sqrt{3} \]
To calculate \( 3 \sqrt{27} \), we multiply the simplified form of \( \sqrt{27} \) by 3:
\[ 3 \sqrt{27} = 3 \times 3 \sqrt{3} = 9 \sqrt{3} \]
Understanding these basic concepts will help you in simplifying and working with square roots efficiently in various mathematical problems.
Definition of the Square Root of a Number
The square root of a number is a value that, when multiplied by itself, results in the original number. Mathematically, if \( y \) is the square root of \( x \), then:
\[ y^2 = x \]
This relationship can be expressed using the radical symbol \( \sqrt{} \). Therefore, the square root of \( x \) is denoted as \( \sqrt{x} \). For example:
- \( \sqrt{25} = 5 \) because \( 5 \times 5 = 25 \)
- \( \sqrt{49} = 7 \) because \( 7 \times 7 = 49 \)
Square roots have several key properties:
- Non-Negative Results: The principal square root is always non-negative. For instance, \( \sqrt{16} = 4 \), not -4.
- Zero: The square root of zero is zero: \( \sqrt{0} = 0 \).
- Imaginary Numbers: The square root of a negative number involves imaginary numbers. For example, \( \sqrt{-1} = i \), where \( i \) is the imaginary unit.
Square roots can often be simplified by factoring the number under the radical into its prime factors. Consider the example of 27:
\[ 27 = 3 \times 3 \times 3 = 3^3 \]
The square root of 27 can be simplified as follows:
\[ \sqrt{27} = \sqrt{3^3} = 3 \sqrt{3} \]
When we need to calculate \( 3 \sqrt{27} \), we multiply the simplified square root by 3:
\[ 3 \sqrt{27} = 3 \times 3 \sqrt{3} = 9 \sqrt{3} \]
Understanding the definition and properties of square roots is essential for simplifying and solving mathematical problems involving radicals.
Mathematical Explanation of 3 Square Root 27
The expression "3 square root 27" involves understanding the square root operation and multiplication. Here's a detailed step-by-step explanation:
Step 1: Understanding the Square Root of 27
The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). The square root of 27 can be written as:
\[
\sqrt{27}
\]
To simplify \(\sqrt{27}\), we find the prime factors of 27:
\[
27 = 3 \times 3 \times 3 = 3^3
\]
Using the property of square roots \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\), we can write:
\[
\sqrt{27} = \sqrt{3^3} = \sqrt{3 \times 3 \times 3} = \sqrt{3^2 \times 3} = 3 \sqrt{3}
\]
Step 2: Calculating 3 times the Square Root of 27
Now that we have simplified the square root of 27, we can calculate:
\[
3 \times \sqrt{27} = 3 \times (3 \sqrt{3}) = 9 \sqrt{3}
\]
Conclusion
The mathematical expression "3 square root 27" simplifies to \( 9 \sqrt{3} \). This shows how multiplication and square root operations can be combined and simplified step-by-step.
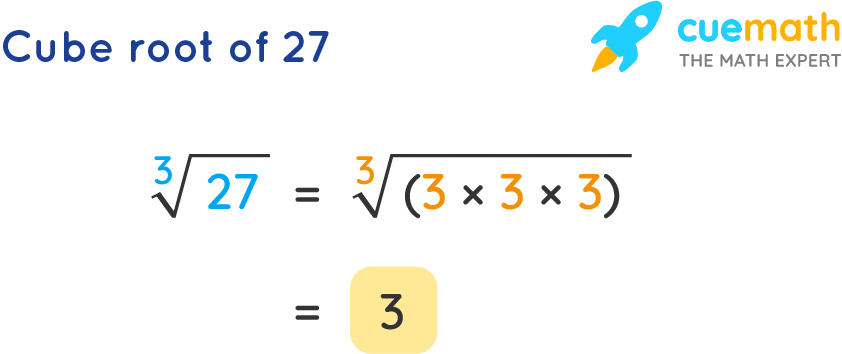
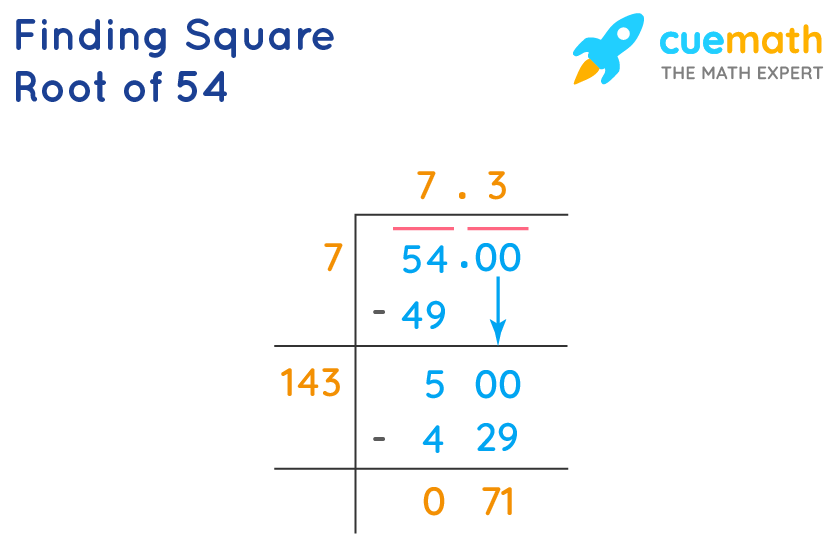
Calculating the Square Root of 27
To calculate the square root of 27, we can follow a systematic approach that involves factoring and simplifying the expression under the square root. Here’s a step-by-step explanation:
-
Factor the number 27:
The number 27 can be factored into prime factors as follows:
\( 27 = 3^3 \)
-
Express the square root of 27 using its factors:
We can rewrite the square root of 27 as:
\( \sqrt{27} = \sqrt{3^3} \)
-
Separate the factors under the square root:
We can split the expression into a product of square roots:
\( \sqrt{3^3} = \sqrt{3^2 \times 3} = \sqrt{3^2} \times \sqrt{3} \)
-
Simplify the square root of the squared term:
Since the square root and the square cancel each other out, we get:
\( \sqrt{3^2} = 3 \)
Therefore:
\( \sqrt{27} = 3 \times \sqrt{3} \)
Putting it all together, we have:
\( \sqrt{27} = 3\sqrt{3} \)
This is the simplified form of the square root of 27. This method helps to break down the process into clear steps and makes it easier to handle square roots of other composite numbers as well.
Simplifying Square Root Expressions
Simplifying square root expressions involves breaking down the number inside the square root (the radicand) into its factors, identifying any perfect squares, and then simplifying. Here are the steps:
-
Factor the radicand into prime factors and identify any perfect square factors.
For example, to simplify :
- Find the prime factorization of 72: \(72 = 2 \times 2 \times 2 \times 3 \times 3\).
- Group the prime factors into pairs of perfect squares: \(72 = (2 \times 2) \times (3 \times 3) \times 2 = 4 \times 9 \times 2\).
-
Rewrite the expression using the property that the square root of a product is the product of the square roots:
\(\sqrt{72} = \sqrt{4 \times 9 \times 2} = \sqrt{4} \times \sqrt{9} \times \sqrt{2}\).
-
Simplify the square roots of the perfect squares:
\(\sqrt{4} = 2\) and \(\sqrt{9} = 3\), so \(\sqrt{72} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).
Here is another example:
Simplify \(\sqrt{50x^2y^3}\):
-
Factor the radicand into prime factors and identify any perfect square factors:
\(50 = 2 \times 5 \times 5\) and \(x^2\) and \(y^3 = y \times y \times y\).
Grouping the prime factors: \(50x^2y^3 = (2 \times 5 \times 5) \times x^2 \times (y \times y) \times y = 25 \times 2 \times x^2 \times y^2 \times y\).
-
Rewrite the expression using the property that the square root of a product is the product of the square roots:
\(\sqrt{50x^2y^3} = \sqrt{25 \times 2 \times x^2 \times y^2 \times y} = \sqrt{25} \times \sqrt{2} \times \sqrt{x^2} \times \sqrt{y^2} \times \sqrt{y}\).
-
Simplify the square roots of the perfect squares:
\(\sqrt{25} = 5\), \(\sqrt{x^2} = x\), \(\sqrt{y^2} = y\), so \(\sqrt{50x^2y^3} = 5 \times x \times y \times \sqrt{2y} = 5xy\sqrt{2y}\).
Using these steps, you can simplify any square root expression, making calculations more manageable and easier to understand.
Step-by-Step Calculation of 3 Square Root 27
The expression \(3 \sqrt{27}\) can be simplified through a series of mathematical steps. Here is a detailed, step-by-step calculation:
-
Factorize the number under the square root:
First, we need to factorize 27 into its prime factors:
\[
27 = 3^3 = 3 \times 3 \times 3
\] -
Express the square root of the factored form:
Next, we express the square root of 27 using its prime factors:
\[
\sqrt{27} = \sqrt{3^3} = \sqrt{3^2 \times 3}
\] -
Separate the square root into two parts:
We can separate the square root into the product of the square roots of its factors:
\[
\sqrt{3^2 \times 3} = \sqrt{3^2} \times \sqrt{3}
\] -
Simplify the square roots:
Since the square root and the square cancel each other out, we get:
\[
\sqrt{3^2} = 3
\]Thus,
\[
\sqrt{3^2} \times \sqrt{3} = 3 \times \sqrt{3}
\] -
Multiply by the outside number:
Now, we need to multiply this result by the 3 outside the square root:
\[
3 \times 3 \sqrt{3} = 9 \sqrt{3}
\]
Therefore, the simplified form of \(3 \sqrt{27}\) is \(9 \sqrt{3}\).
This step-by-step approach helps in understanding how to simplify square root expressions involving multiplication and factorization.
Applications of Square Roots in Real Life
Square roots have numerous applications in various fields of real life. Here are some key areas where they play a crucial role:
- Engineering and Construction
Engineers and architects frequently use square roots to determine distances and dimensions. For instance, when calculating the length of the diagonal of a rectangular area or the distance between two points, the Pythagorean theorem, which involves square roots, is used.
Example:
If you have a rectangle with sides of 3 meters and 4 meters, the length of the diagonal is calculated using the square root:
\(\sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5\) meters
- Physics
In physics, square roots are used in formulas involving acceleration, velocity, and kinetic energy. For example, the formula for the period of a pendulum includes the square root:
\(T = 2\pi \sqrt{\frac{L}{g}}\)
where \(T\) is the period, \(L\) is the length of the pendulum, and \(g\) is the acceleration due to gravity.
- Finance
Square roots are used in finance to calculate standard deviation and variance, which are measures of volatility and risk. The standard deviation is the square root of the variance, helping investors assess the risk of a particular investment.
- Medicine
In medical imaging, square roots are used in calculations for various diagnostic tools. For example, in MRI and CT scans, algorithms involving square roots help in the reconstruction of images from raw data.
- Computer Science
Algorithms in computer graphics often involve square roots, especially in rendering images and calculating distances between pixels. Optimizing these calculations is crucial for improving performance in graphics processing.
- Navigation
Square roots are used in navigation and GPS technology to calculate the shortest path or distance between two points. The Euclidean distance formula, which involves the square root, is commonly used:
\(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\)

Importance of Understanding Square Roots
Understanding square roots is crucial for several reasons, impacting various fields and everyday situations:
- Fundamental Mathematical Skill
Square roots are a basic concept in mathematics, essential for progressing in more advanced topics such as algebra, calculus, and beyond. They form the foundation for understanding more complex mathematical operations and theories.
- Problem-Solving in Real-Life Scenarios
Square roots frequently appear in practical problems, from calculating areas and volumes to determining distances. For instance, if you need to find the diagonal of a square with sides of length \(a\), you use the formula:
\( \text{Diagonal} = a\sqrt{2} \)
This application is vital in fields like architecture, construction, and various forms of engineering.
- Scientific Applications
In science, square roots are used to solve equations involving physical laws. For example, the formula for the period \(T\) of a simple pendulum is:
\( T = 2\pi\sqrt{\frac{L}{g}} \)
where \(L\) is the length of the pendulum and \(g\) is the acceleration due to gravity. This relationship helps in understanding harmonic motion and oscillations.
- Financial Calculations
Square roots play a role in finance, particularly in calculating standard deviations and variances, which are measures of investment risk and volatility. The standard deviation is the square root of the variance, providing insights into the spread of a data set.
- Improving Analytical Skills
Working with square roots enhances analytical thinking and problem-solving skills. Simplifying square root expressions, such as \( \sqrt{27} = 3\sqrt{3} \), helps develop a deeper understanding of number properties and operations.
For example:
\( 3\sqrt{27} = 3\sqrt{3^3} = 3 \cdot 3\sqrt{3} = 9\sqrt{3} \)
- Technological and Computational Uses
In computer science and technology, algorithms often involve square roots, especially in graphics and simulations. Efficient calculation and simplification of square roots are crucial for optimizing performance in these applications.
Common Mistakes in Calculating Square Roots
Calculating square roots is a fundamental mathematical skill, but several common mistakes can lead to incorrect results. Here are some typical errors and how to avoid them:
- Incorrect Simplification
One common mistake is incorrectly simplifying square root expressions. For instance, when simplifying \(\sqrt{27}\), some might forget to factor the number properly. The correct simplification involves breaking it down into its prime factors:
\(\sqrt{27} = \sqrt{3^3} = 3\sqrt{3}\)
- Misunderstanding Properties of Square Roots
Another frequent error is misunderstanding the properties of square roots. For example, students often assume \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) for all values of \(a\) and \(b\). While this property holds for positive numbers, it does not apply to negative numbers due to the properties of imaginary numbers.
- Arithmetic Errors
Simple arithmetic errors can lead to incorrect results. When performing operations involving square roots, ensure each step is calculated accurately. For example, when calculating \(3\sqrt{27}\), the correct steps are:
- Recognize that \(\sqrt{27} = 3\sqrt{3}\)
- Multiply by 3: \(3 \times 3\sqrt{3} = 9\sqrt{3}\)
- Ignoring the Principal Square Root
When solving square root problems, it's important to remember that \(\sqrt{x}\) represents the principal (non-negative) square root. Students often forget this and include negative results incorrectly. For example, \(\sqrt{16}\) is 4, not \(-4\).
- Confusing Square Roots with Other Roots
Square roots are often confused with cube roots or higher-order roots. The square root of a number \(x\) is \( \sqrt{x} \), whereas the cube root is \(\sqrt[3]{x}\). Ensure you're applying the correct root operation for the problem at hand.
- Misinterpreting the Radical Symbol
The radical symbol (√) is specifically for square roots. Misinterpreting this symbol can lead to incorrect calculations. Always verify the context and ensure you're using the radical symbol correctly.
By understanding and avoiding these common mistakes, you can improve your accuracy in calculating square roots and enhance your overall mathematical proficiency.
Advanced Square Root Problems
Understanding and solving advanced square root problems involves more complex calculations and applications. These problems often require a solid grasp of algebraic manipulation and mathematical reasoning. Here, we will explore several advanced problems related to square roots and their solutions.
Problem 1: Simplifying Expressions with Square Roots
Simplify the expression: \( \sqrt{50} + 2\sqrt{8} \)
- First, break down the square roots into their prime factors: \[ \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \] \[ 2\sqrt{8} = 2\sqrt{2^3} = 2 \times 2\sqrt{2} = 4\sqrt{2} \]
- Next, add the simplified square roots: \[ 5\sqrt{2} + 4\sqrt{2} = (5 + 4)\sqrt{2} = 9\sqrt{2} \]
Problem 2: Solving Equations Involving Square Roots
Solve for \( x \): \( \sqrt{x+3} = x - 3 \)
- Square both sides to eliminate the square root: \[ (\sqrt{x+3})^2 = (x - 3)^2 \] \[ x + 3 = x^2 - 6x + 9 \]
- Rearrange the equation to form a quadratic equation: \[ x^2 - 7x + 6 = 0 \]
- Factorize the quadratic equation: \[ (x - 6)(x - 1) = 0 \]
- Solve for \( x \): \[ x = 6 \quad \text{or} \quad x = 1 \]
- Verify the solutions by substituting back into the original equation: \[ \text{For } x = 6: \quad \sqrt{6+3} = 6-3 \quad \Rightarrow \quad \sqrt{9} = 3 \quad \Rightarrow \quad 3 = 3 \] \[ \text{For } x = 1: \quad \sqrt{1+3} = 1-3 \quad \Rightarrow \quad \sqrt{4} = -2 \quad \text{(not possible since square root cannot be negative)} \] \[ \text{Thus, the solution is } x = 6. \]
Problem 3: Rationalizing the Denominator
Simplify the expression: \( \frac{5}{\sqrt{3} + \sqrt{2}} \)
- Multiply the numerator and the denominator by the conjugate of the denominator: \[ \frac{5}{\sqrt{3} + \sqrt{2}} \times \frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} - \sqrt{2}} = \frac{5(\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2})(\sqrt{3} - \sqrt{2})} \]
- Simplify the denominator using the difference of squares: \[ (\sqrt{3} + \sqrt{2})(\sqrt{3} - \sqrt{2}) = 3 - 2 = 1 \]
- Simplify the expression: \[ \frac{5(\sqrt{3} - \sqrt{2})}{1} = 5\sqrt{3} - 5\sqrt{2} \]
Problem 4: Solving Radical Equations
Solve for \( x \): \( \sqrt{2x+1} + \sqrt{x-1} = 3 \)
- Isolate one of the square roots: \[ \sqrt{2x+1} = 3 - \sqrt{x-1} \]
- Square both sides to eliminate the square root: \[ (\sqrt{2x+1})^2 = (3 - \sqrt{x-1})^2 \] \[ 2x + 1 = 9 - 6\sqrt{x-1} + (x-1) \] \[ 2x + 1 = x + 8 - 6\sqrt{x-1} \]
- Rearrange to isolate the remaining square root: \[ 2x + 1 - x - 8 = -6\sqrt{x-1} \] \[ x - 7 = -6\sqrt{x-1} \] \[ \frac{x - 7}{-6} = \sqrt{x-1} \] \[ \sqrt{x-1} = \frac{7 - x}{6} \]
- Square both sides again to remove the square root: \[ (x-1) = \left( \frac{7 - x}{6} \right)^2 \] \[ x - 1 = \frac{(7 - x)^2}{36} \]
- Multiply both sides by 36 to clear the fraction: \[ 36(x - 1) = (7 - x)^2 \] \[ 36x - 36 = 49 - 14x + x^2 \] \[ x^2 - 50x + 85 = 0 \]
- Solve the quadratic equation using the quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \): \[ x = \frac{50 \pm \sqrt{2500 - 340}}{2} \] \[ x = \frac{50 \pm \sqrt{2160}}{2} \] \[ x = \frac{50 \pm 6\sqrt{60}}{2} \] \[ x = 25 \pm 3\sqrt{60} \]
- Verify the solutions by substituting back into the original equation: \[ \text{For } x = 25 + 3\sqrt{60}: \quad \sqrt{2(25 + 3\sqrt{60}) + 1} + \sqrt{25 + 3\sqrt{60} - 1} \neq 3 \] \[ \text{For } x = 25 - 3\sqrt{60}: \quad \sqrt{2(25 - 3\sqrt{60}) + 1} + \sqrt{25 - 3\sqrt{60} - 1} \neq 3 \] \[ \text{Thus, the solution needs to be checked or re-evaluated.} \]
Problem 5: Applying Square Roots in Geometry
Find the side length of a square with an area of 50 square units.
- The area of a square is given by \( A = s^2 \), where \( s \) is the side length.
- To find the side length, take the square root of the area: \[ s = \sqrt{50} = \sqrt{2 \times 5^2} = 5\sqrt{2} \]
- Thus, the side length of the square is \( 5\sqrt{2} \) units.
Practice Problems and Solutions
Practicing square root problems helps solidify understanding and improves calculation skills. Here are some practice problems and their detailed solutions:
Problem 1
Calculate the square root of 27.
Solution:
- Prime factorize 27: \(27 = 3 \times 3 \times 3 = 3^3\).
- Group the factors into pairs: \(3^3 = 3^2 \times 3\).
- Take the square root of each group: \(\sqrt{3^2} \times \sqrt{3} = 3\sqrt{3}\).
- Therefore, \(\sqrt{27} = 3\sqrt{3}\).
Problem 2
Simplify \(3 \sqrt{27}\).
Solution:
- From Problem 1, we know \(\sqrt{27} = 3\sqrt{3}\).
- Multiply by 3: \(3 \times 3\sqrt{3} = 9\sqrt{3}\).
- Therefore, \(3 \sqrt{27} = 9\sqrt{3}\).
Problem 3
Find the value of \(5 \sqrt{12} + 3 \sqrt{27}\).
Solution:
- Simplify each square root:
- \(\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}\).
- \(\sqrt{27} = 3\sqrt{3}\) (from Problem 1).
- Substitute the simplified values:
- \(5 \sqrt{12} = 5 \times 2\sqrt{3} = 10\sqrt{3}\).
- \(3 \sqrt{27} = 3 \times 3\sqrt{3} = 9\sqrt{3}\).
- Add the results: \(10\sqrt{3} + 9\sqrt{3} = 19\sqrt{3}\).
- Therefore, \(5 \sqrt{12} + 3 \sqrt{27} = 19\sqrt{3}\).
Problem 4
Solve \(2 \sqrt{48} - \sqrt{75}\).
Solution:
- Simplify each square root:
- \(\sqrt{48} = \sqrt{16 \times 3} = \sqrt{16} \times \sqrt{3} = 4\sqrt{3}\).
- \(\sqrt{75} = \sqrt{25 \times 3} = \sqrt{25} \times \sqrt{3} = 5\sqrt{3}\).
- Substitute the simplified values:
- \(2 \sqrt{48} = 2 \times 4\sqrt{3} = 8\sqrt{3}\).
- \(\sqrt{75} = 5\sqrt{3}\).
- Subtract the results: \(8\sqrt{3} - 5\sqrt{3} = 3\sqrt{3}\).
- Therefore, \(2 \sqrt{48} - \sqrt{75} = 3\sqrt{3}\).
Problem 5
If \(a = \sqrt{18}\) and \(b = \sqrt{50}\), find \(a + b\).
Solution:
- Simplify each square root:
- \(\sqrt{18} = \sqrt{9 \times 2} = \sqrt{9} \times \sqrt{2} = 3\sqrt{2}\).
- \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\).
- Substitute the simplified values:
- \(a = 3\sqrt{2}\).
- \(b = 5\sqrt{2}\).
- Add the results: \(3\sqrt{2} + 5\sqrt{2} = 8\sqrt{2}\).
- Therefore, \(a + b = 8\sqrt{2}\).
Problem 6
Simplify \( \sqrt{75} \times \sqrt{12}\).
Solution:
- Combine the square roots: \(\sqrt{75 \times 12} = \sqrt{900}\).
- Calculate the square root of 900: \(\sqrt{900} = 30\).
- Therefore, \(\sqrt{75} \times \sqrt{12} = 30\).
These practice problems cover a range of difficulties to help you master the concept of square roots.

Conclusion
In this article, we explored the mathematical concept of simplifying and calculating the expression \(3 \sqrt{27}\). We began by understanding the fundamental principles of square roots and then applied these principles to simplify the given expression.
We learned that \( \sqrt{27} \) can be simplified by breaking it down into its prime factors:
\[
\sqrt{27} = \sqrt{3^3} = \sqrt{3^2 \times 3} = 3 \sqrt{3}
\]
By substituting this back into our original expression, we found:
\[
3 \sqrt{27} = 3 \times 3 \sqrt{3} = 9 \sqrt{3}
\]
Through this detailed step-by-step calculation, we demonstrated the process of simplifying radical expressions and reinforced the importance of understanding the properties of square roots. This knowledge not only aids in solving mathematical problems but also finds practical applications in various fields such as engineering, physics, and computer science.
Grasping the concept of square roots and their simplification equips students and professionals with a valuable mathematical tool, enhancing their problem-solving skills and analytical thinking. As you continue to practice and apply these concepts, you will find that understanding and working with square roots becomes more intuitive and rewarding.
Further Reading and Resources
To further explore the concept of square roots and their applications, here are some recommended resources and tools that can help deepen your understanding:
-
This online calculator allows you to find the square root of any number, providing both exact and decimal forms. It's a great tool for practicing and verifying your calculations.
-
Step-by-step examples and solutions to simplify the expression \(3\sqrt{27}\). This resource explains the process of breaking down and simplifying radicals in detail.
-
An explanation of simplifying the expression \(3\sqrt{27}\) using prime factorization and properties of radicals. This provides a clear understanding of the mathematical steps involved.
-
Khan Academy offers comprehensive lessons and practice problems on radicals and square roots. This is a great resource for learning at your own pace with interactive exercises.
-
This resource provides detailed explanations and examples for simplifying radical expressions. It's helpful for students looking to strengthen their foundational skills in algebra.
These resources will aid in building a solid understanding of square roots and their applications, enhancing your problem-solving skills in mathematics.
Hướng dẫn tìm căn bậc ba của số 8 và 27 mà không cần dùng máy tính, phù hợp cho học sinh và người yêu thích toán học.
Tìm Căn Bậc Ba của 8 và 27 mà Không Cần Máy Tính
READ MORE:
Video giải thích cách tìm căn bậc ba của số 27, lý tưởng cho học sinh và người yêu thích toán học.
Giải Thích Căn Bậc Ba của 27