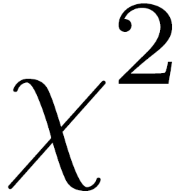Topic what does x squared equal: What does x squared equal? This fundamental question opens the door to a deeper understanding of algebra. By exploring the definition, properties, and applications of x squared, we can better appreciate its significance in mathematics. Join us as we delve into this essential concept and discover its various uses and solutions.
Table of Content
- Understanding What x Squared Equals
- Introduction to x Squared
- Definition and Basic Concept of x Squared
- Examples of x Squared in Mathematics
- Properties of x Squared
- Graphical Representation of x Squared
- Perfect Squares and Their Importance
- Solving Equations Involving x Squared
- Quadratic Equations and x Squared
- Methods to Solve Quadratic Equations
- Applications of x Squared in Real Life
- Practice Problems and Solutions
- Conclusion
- YOUTUBE: Hướng dẫn chi tiết cách giải phương trình x bình phương = 4 và các giá trị bình phương khác của x. Video này sẽ giúp bạn hiểu rõ hơn về các phương trình bậc hai và cách giải chúng.
Understanding What x Squared Equals
The expression \( x^2 \) or "x squared" refers to the value obtained when a number, \( x \), is multiplied by itself. This is a fundamental concept in algebra and appears frequently in various mathematical equations and real-world applications.
Definition
In mathematical terms, \( x^2 \) can be defined as:
\[
x^2 = x \times x
\]
Examples
- If \( x = 2 \), then \( x^2 = 2 \times 2 = 4 \).
- If \( x = -3 \), then \( x^2 = (-3) \times (-3) = 9 \).
- If \( x = 5 \), then \( x^2 = 5 \times 5 = 25 \).
Properties of \( x^2 \)
- \( x^2 \) is always non-negative, regardless of whether \( x \) is positive or negative.
- The graph of \( y = x^2 \) is a parabola opening upwards.
Perfect Squares
A perfect square is an integer that is the square of another integer. For example:
- \( 1^2 = 1 \)
- \( 2^2 = 4 \)
- \( 3^2 = 9 \)
- \( 4^2 = 16 \)
- \( 5^2 = 25 \)
Solving Equations Involving \( x^2 \)
Equations that involve \( x^2 \) are often quadratic equations, which can be written in the standard form:
\[
ax^2 + bx + c = 0
\]
These equations can be solved using various methods such as factoring, completing the square, or using the quadratic formula:
\[
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\]
Applications
Understanding \( x^2 \) is crucial in many areas of mathematics and science, including:
- Calculating areas of squares.
- Solving physics problems involving motion and forces.
- Analyzing quadratic functions in algebra.
Practice Problems
- Solve for \( x \): \( x^2 = 16 \).
- Solve for \( x \): \( x^2 - 9 = 0 \).
- Solve the quadratic equation: \( 2x^2 + 3x - 2 = 0 \).
READ MORE:
Introduction to x Squared
Understanding the concept of x squared is fundamental in algebra and mathematics as a whole. Squaring a number means multiplying the number by itself. This concept applies not only to integers but also to variables. The notation for squaring a number or variable is typically written as \(x^2\), where the superscript 2 denotes the squaring operation.
Let's break down the process of squaring with some examples and applications:
- Squaring a Positive Number: For any positive number \(a\), squaring it results in \(a \times a = a^2\). For example, \(3^2 = 3 \times 3 = 9\).
- Squaring a Negative Number: When squaring a negative number, the result is positive because a negative times a negative equals a positive. For instance, \((-4)^2 = (-4) \times (-4) = 16\).
- Squaring Zero: The square of zero is zero, \(0^2 = 0 \times 0 = 0\).
One important application of squaring is in finding the area of a square. If the side length of a square is \(x\), the area is calculated as \(x^2\). Additionally, squaring is used in various algebraic formulas and solving quadratic equations.
In algebra, solving the equation \(x^2 = a\) involves finding the square roots of \(a\). The solutions are \(x = \sqrt{a}\) and \(x = -\sqrt{a}\), acknowledging that both positive and negative roots are valid for non-negative \(a\).
Definition and Basic Concept of x Squared
The concept of \( x^2 \) or "x squared" is fundamental in mathematics, particularly in algebra. Squaring a number means multiplying it by itself. For instance, if \( x \) is 3, then \( x^2 \) is 3 * 3, which equals 9.
Here are some essential points about \( x^2 \):
- Squaring a number always results in a non-negative value. This is because both positive and negative numbers become positive when multiplied by themselves. For example, \( 4^2 = 16 \) and \((-4)^2 = 16\).
- The notation \( x^2 \) is read as "x squared" and indicates that the base number \( x \) is raised to the power of 2.
- The square of a number is a special case of exponentiation where the exponent is 2.
Understanding squares is crucial for solving quadratic equations and understanding geometric concepts, such as the area of a square.
Let's look at the definition and properties of squaring more formally:
- Definition: For any real number \( x \), \( x^2 \) is defined as \( x \times x \).
- Properties:
- Non-negativity: \( x^2 \geq 0 \) for all \( x \in \mathbb{R} \). Even when \( x \) is negative, \( x^2 \) is positive.
- Symmetry: \( x^2 \) is the same whether \( x \) is positive or negative. For example, \( 5^2 = 25 \) and \((-5)^2 = 25\).
- Quadratic nature: Squaring a number is a type of quadratic operation, which is fundamental in quadratic equations and functions. The standard form of a quadratic equation is \( ax^2 + bx + c = 0 \).
Understanding \( x^2 \) is essential for many areas of mathematics and science, as it forms the basis for more complex concepts like quadratic equations, parabolas, and the Pythagorean theorem.
Examples of x Squared in Mathematics
Understanding x squared (\(x^2\)) is fundamental in mathematics. Here are some detailed examples demonstrating its use:
Example 1: Simple Calculation
To find the value of \(x^2\) for a specific x, simply multiply the number by itself.
- For \(x = 3\), \(x^2 = 3^2 = 3 \times 3 = 9\)
- For \(x = -4\), \(x^2 = (-4)^2 = (-4) \times (-4) = 16\)
Example 2: Solving Equations
Consider the equation \(x^2 = 16\). To solve for x, we take the square root of both sides:
\[\sqrt{x^2} = \sqrt{16}\]
This gives us \(x = 4\) or \(x = -4\), since both \(4^2\) and \((-4)^2\) equal 16.
Example 3: Area of a Square
The area of a square is found using the formula \(A = x^2\), where x is the length of a side.
If a square has an area of 25 square units, we can find the side length as follows:
\[x^2 = 25\]
\[x = \sqrt{25} = 5\]
Therefore, each side of the square is 5 units long.
Example 4: Quadratic Equations
Quadratic equations often involve \(x^2\). For example, consider the quadratic equation \(x^2 - 5x + 6 = 0\). To solve it, we factorize the quadratic expression:
\[x^2 - 5x + 6 = (x - 2)(x - 3) = 0\]
This gives us the solutions \(x = 2\) and \(x = 3\).
Example 5: Graphing \(x^2\)
The function \(y = x^2\) represents a parabola when graphed. It opens upwards, and its vertex is at the origin (0,0). The graph is symmetric about the y-axis. Here's a table of values:
| x | y = x^2 |
|---|---|
| -3 | 9 |
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
Example 6: Difference of Squares
Consider the expression \(x^4 - 16\). This can be factorized using the difference of squares formula:
\[x^4 - 16 = (x^2)^2 - 4^2 = (x^2 + 4)(x^2 - 4)\]
The term \(x^2 - 4\) can be further factorized:
\[x^2 - 4 = (x + 2)(x - 2)\]
Thus, the full factorization is:
\[x^4 - 16 = (x^2 + 4)(x + 2)(x - 2)\]
These examples illustrate the versatility and importance of \(x^2\) in various mathematical contexts.
Properties of x Squared
The properties of \(x^2\) are fundamental in understanding various aspects of mathematics, from basic arithmetic to advanced algebra. Below, we explore several key properties of \(x^2\).
-
Non-negativity:
The value of \(x^2\) is always non-negative. This means that for any real number \(x\), \(x^2 \geq 0\). Whether \(x\) is positive, negative, or zero, squaring \(x\) results in a non-negative number.
\(\text{Example: } x = -3, \, x^2 = (-3)^2 = 9\)
-
Zero Property:
If \(x^2 = 0\), then \(x\) must be 0. This is because 0 is the only number whose square is 0.
\(\text{Example: } x = 0, \, x^2 = 0^2 = 0\)
-
Symmetry:
Squaring a number preserves symmetry. Specifically, \((x^2)\) and \((-x)^2\) yield the same result. This property shows that the square of both a number and its negative are identical.
\(\text{Example: } x = 4, \, x^2 = 4^2 = 16\) and \(\text{-}x = -4, \, (-4)^2 = 16\)
-
Parabolic Graph:
The graph of \(y = x^2\) is a parabola that opens upwards. This graph is symmetric with respect to the y-axis.

-
Algebraic Identity:
The square of a binomial can be expanded using the formula \((a + b)^2 = a^2 + 2ab + b^2\). Similarly, \((a - b)^2 = a^2 - 2ab + b^2\).
\(\text{Example: } (x + 3)^2 = x^2 + 6x + 9\)
-
Multiplication Property:
The product of two squares is the square of the product of the numbers. That is, \((xy)^2 = x^2 y^2\).
\(\text{Example: } (2 \cdot 3)^2 = 6^2 = 36 \text{ and } 2^2 \cdot 3^2 = 4 \cdot 9 = 36\)
These properties illustrate the simplicity yet profound impact of squaring a number. Understanding these helps in solving quadratic equations, graphing parabolas, and exploring further algebraic concepts.

Graphical Representation of x Squared
The function \( x^2 \) is a fundamental mathematical expression that represents a parabola in a two-dimensional coordinate system. To understand its graphical representation, consider the following details:
1. Basic Shape
The graph of \( y = x^2 \) is a parabola that opens upwards. The vertex of the parabola is at the origin (0, 0), which is the minimum point of the curve.
2. Key Characteristics
- Axis of Symmetry: The graph is symmetric about the y-axis. This means that for every point (x, y) on the graph, there is a corresponding point (-x, y).
- Vertex: The lowest point of the parabola is the vertex at (0, 0).
- Direction: The parabola opens upwards, indicating that the function has a minimum value at the vertex.
3. Plotting Points
To draw the graph of \( y = x^2 \), you can plot points for different values of x and connect them smoothly:
| x | y = x2 |
|---|---|
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
4. Graphical Visualization
Using MathJax, we can represent the equation graphically:
Below is the graph of \( y = x^2 \):

5. Detailed Steps
- Start at the origin (0,0) which is the vertex of the parabola.
- Plot points on either side of the origin, such as (-2, 4), (-1, 1), (1, 1), and (2, 4).
- Draw a smooth curve through these points to complete the parabola.
This visual representation helps in understanding how the values of \( x \) and \( x^2 \) correlate to form a parabolic shape. The symmetry and the vertex are key features that define the nature of the \( x^2 \) graph.
Perfect Squares and Their Importance
A perfect square is an integer that is the square of another integer. In other words, a number \( n \) is a perfect square if there exists an integer \( m \) such that \( n = m^2 \). Perfect squares have significant importance in various fields of mathematics and real-world applications.
1. Definition of Perfect Squares
Perfect squares are numbers that can be expressed as the product of an integer with itself. For example:
- \(1 = 1^2\)
- \(4 = 2^2\)
- \(9 = 3^2\)
- \(16 = 4^2\)
- \(25 = 5^2\)
2. Properties of Perfect Squares
- Perfect squares are always non-negative.
- The square root of a perfect square is always an integer.
- The number of factors of a perfect square is always odd.
- When a perfect square is expressed in prime factorization, all the exponents are even.
3. List of Some Perfect Squares
| Number | Perfect Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
4. Importance of Perfect Squares
Perfect squares play a crucial role in various aspects of mathematics and everyday life:
- Algebra: Perfect squares simplify the process of factoring and solving quadratic equations.
- Geometry: The concept of perfect squares is used in calculating the area of squares, which is essential in geometry.
- Number Theory: They are fundamental in the study of number properties and integer relationships.
- Computing: Efficient algorithms for checking perfect squares are crucial in computer science.
5. Applications of Perfect Squares
- In real-world scenarios, perfect squares are used in design and construction to ensure precise measurements and calculations.
- They are essential in financial calculations, such as determining areas for landscaping and architectural designs.
- In statistics, the sum of squared deviations is a critical measure used in various data analyses.
Understanding perfect squares and their properties provides a strong foundation for further mathematical study and practical applications.
Solving Equations Involving x Squared
When solving equations that involve x squared, we are typically dealing with quadratic equations. These equations take the general form:
\( ax^2 + bx + c = 0 \)
Here, a, b, and c are constants, and x is the variable to be solved. There are several methods to solve quadratic equations:
1. Factoring
Factoring involves expressing the quadratic equation as a product of two binomials. For example:
\( x^2 + 5x + 6 = 0 \)
can be factored as:
\( (x + 2)(x + 3) = 0 \)
Setting each factor equal to zero gives us the solutions:
\( x + 2 = 0 \) or \( x + 3 = 0 \)
Thus, the solutions are:
\( x = -2 \) and \( x = -3 \)
2. Using the Quadratic Formula
For any quadratic equation \( ax^2 + bx + c = 0 \), the solutions can be found using the quadratic formula:
\( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)
Example: Solve \( 2x^2 + 3x - 2 = 0 \)
Here, a = 2, b = 3, and c = -2. Plugging these values into the quadratic formula gives:
\( x = \frac{-3 \pm \sqrt{3^2 - 4(2)(-2)}}{2(2)} = \frac{-3 \pm \sqrt{9 + 16}}{4} = \frac{-3 \pm \sqrt{25}}{4} = \frac{-3 \pm 5}{4} \)
This yields two solutions:
\( x = \frac{2}{4} = \frac{1}{2} \) and \( x = \frac{-8}{4} = -2 \)
3. Completing the Square
Completing the square transforms the quadratic equation into a perfect square trinomial. Consider the equation:
\( x^2 + 6x + 5 = 0 \)
First, move the constant term to the other side:
\( x^2 + 6x = -5 \)
Next, add the square of half the coefficient of x to both sides:
\( x^2 + 6x + 9 = -5 + 9 \)
Now, we have a perfect square trinomial on the left:
\( (x + 3)^2 = 4 \)
Taking the square root of both sides:
\( x + 3 = \pm 2 \)
This gives us two solutions:
\( x = -1 \) and \( x = -5 \)
4. Graphical Method
Solving the quadratic equation graphically involves plotting the quadratic function \( y = ax^2 + bx + c \) and finding the points where the graph intersects the x-axis. These points are the solutions of the equation.
Example: For \( y = x^2 - 4x + 3 \), the graph intersects the x-axis at \( x = 1 \) and \( x = 3 \), hence these are the solutions.
Using these methods, you can solve any quadratic equation. Practice with different equations to become proficient in each technique.
Quadratic Equations and x Squared
Quadratic equations are polynomial equations of the form \( ax^2 + bx + c = 0 \), where \( a \), \( b \), and \( c \) are constants, and \( a \neq 0 \). These equations are fundamental in algebra and have various methods of solution.
Standard Form of a Quadratic Equation
The standard form of a quadratic equation is:
\[ ax^2 + bx + c = 0 \]
Here, \( x \) represents an unknown variable, while \( a \), \( b \), and \( c \) are coefficients where \( a \neq 0 \). The term \( ax^2 \) is the quadratic term, \( bx \) is the linear term, and \( c \) is the constant term.
Methods to Solve Quadratic Equations
There are several methods to solve quadratic equations, including:
- Factoring
- Completing the Square
- Using the Quadratic Formula
- Graphical Methods
1. Factoring
Factoring involves writing the quadratic equation as a product of its linear factors. For example:
\[ x^2 + 5x + 6 = 0 \]
Can be factored into:
\[ (x + 2)(x + 3) = 0 \]
Setting each factor to zero gives the solutions \( x = -2 \) and \( x = -3 \).
2. Completing the Square
This method involves rearranging the equation to form a perfect square trinomial. For example:
\[ x^2 + 6x + 5 = 0 \]
Can be rewritten as:
\[ (x + 3)^2 - 4 = 0 \]
Then solving for \( x \) by isolating the squared term and taking the square root of both sides.
3. Using the Quadratic Formula
The quadratic formula provides a direct way to find the roots of any quadratic equation:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Here, \( b^2 - 4ac \) is called the discriminant. It determines the nature of the roots:
- If the discriminant is positive, there are two distinct real roots.
- If the discriminant is zero, there is exactly one real root (a repeated root).
- If the discriminant is negative, there are two complex roots.
4. Graphical Methods
Graphing the quadratic function \( y = ax^2 + bx + c \) provides a visual representation of the roots. The points where the graph intersects the x-axis are the solutions to the quadratic equation.
Example: Solving Using the Quadratic Formula
Consider the quadratic equation \( 2x^2 - 4x - 6 = 0 \). To solve this using the quadratic formula, we identify \( a = 2 \), \( b = -4 \), and \( c = -6 \). Plugging these into the formula gives:
\[ x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(2)(-6)}}{2(2)} \]
Simplifying under the square root:
\[ x = \frac{4 \pm \sqrt{16 + 48}}{4} \]
\[ x = \frac{4 \pm \sqrt{64}}{4} \]
\[ x = \frac{4 \pm 8}{4} \]
This gives two solutions:
\[ x = 3 \quad \text{and} \quad x = -1 \]
Importance of Quadratic Equations
Quadratic equations are used in various real-life applications, including physics, engineering, economics, and biology. They model phenomena such as projectile motion, area optimization, and population dynamics.
Understanding and solving quadratic equations is a crucial skill in mathematics, providing a foundation for more advanced topics in algebra and calculus.

Methods to Solve Quadratic Equations
There are several methods to solve quadratic equations, each with its own approach. The most common methods include:
1. Factoring
Factoring involves expressing the quadratic equation as a product of its linear factors. For example, to solve \( x^2 + 5x + 6 = 0 \), we factor it as:
\[ (x + 2)(x + 3) = 0 \]
Setting each factor to zero gives the solutions \( x = -2 \) and \( x = -3 \).
2. Completing the Square
Completing the square involves rearranging the quadratic equation to form a perfect square trinomial. For instance, consider \( x^2 - 10x + 16 = 0 \). We can rewrite it as:
\[ x^2 - 10x + 25 - 25 + 16 = 0 \]
\[ (x - 5)^2 - 9 = 0 \]
Then, solving for \( x \):
\[ (x - 5)^2 = 9 \]
\[ x - 5 = \pm 3 \]
Thus, \( x = 8 \) or \( x = 2 \).
3. Using the Quadratic Formula
The quadratic formula is a universal method for solving any quadratic equation. Given \( ax^2 + bx + c = 0 \), the solutions are:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
The term \( b^2 - 4ac \) is known as the discriminant and it determines the nature of the roots:
- If the discriminant is positive, there are two distinct real roots.
- If the discriminant is zero, there is exactly one real root.
- If the discriminant is negative, there are two complex roots.
4. Graphical Method
Graphing the quadratic function \( y = ax^2 + bx + c \) can provide a visual representation of the solutions. The x-intercepts of the graph (where \( y = 0 \)) are the solutions to the quadratic equation.
Example: Solving Using the Quadratic Formula
Consider the quadratic equation \( 2x^2 - 4x - 6 = 0 \). Using the quadratic formula:
\[ a = 2, \, b = -4, \, c = -6 \]
Plugging in these values:
\[ x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(2)(-6)}}{2(2)} \]
\[ x = \frac{4 \pm \sqrt{16 + 48}}{4} \]
\[ x = \frac{4 \pm \sqrt{64}}{4} \]
\[ x = \frac{4 \pm 8}{4} \]
Therefore, the solutions are \( x = 3 \) and \( x = -1 \).
Applications of x Squared in Real Life
The concept of \(x^2\) or squaring a number has numerous practical applications in various fields. Here are some detailed examples:
1. Finance
In finance, squaring is used to calculate stock market volatility, which measures how much a stock's price varies over time. The standard deviation, a key metric for assessing investment risk, is derived from the variance of stock returns, where variance is the average of the squared differences from the mean.
2. Architecture and Engineering
Architects and engineers use squares to determine the natural frequency of structures such as bridges and buildings, helping predict how these structures will respond to different loads. For instance, the vibration of a bridge under traffic can be analyzed using these principles to ensure safety and durability.
3. Science
In various scientific fields, squaring is vital. For example:
- Physics: The kinetic energy of an object is calculated as \( \frac{1}{2}mv^2 \), where \(v\) is the velocity.
- Astronomy: The square of the orbital speed of planets helps in understanding their motion around stars.
4. Sports
In sports, particularly those involving projectile motion like basketball or javelin throw, quadratic equations help determine the optimal angle and velocity for achieving the best results. The trajectory of the ball or object can be modeled using \( y = ax^2 + bx + c \), where \(a\), \(b\), and \(c\) are constants.
5. Agriculture
Farmers use quadratic equations to optimize land usage. For instance, if they need to fence a rectangular area with a given amount of fencing, they can use quadratic equations to maximize the enclosed area. This involves calculating the dimensions that will give the largest possible area.
6. Projectile Motion in Defense
In the military, calculating the trajectory of projectiles involves quadratic equations. The path of artillery shells or missiles is determined by their initial velocity and the angle of launch, modeled by the equation \( y = ax^2 + bx + c \).
7. Management and Business
Managers use quadratic equations to model and solve problems related to cost, revenue, and profit. For example, the profit maximization problem can be modeled using a quadratic function where the maximum profit occurs at the vertex of the parabola described by the profit function \( P(x) = ax^2 + bx + c \).
8. Navigation and Mapping
In navigation, quadratic equations help in determining distances and plotting courses. The Pythagorean theorem, which involves squaring the sides of a right triangle, is essential in calculating the shortest path between two points.
9. Computer Graphics and Cryptography
In computer graphics, squares and square roots are used in algorithms for rendering images and animations. Cryptography uses these mathematical concepts to secure data through encryption methods that rely on the properties of numbers and their squares.
10. Everyday Calculations
From calculating areas of rooms for flooring to determining the correct dosage of medication based on body weight (which often involves squaring the weight), the application of \(x^2\) is pervasive in daily life.
Understanding the applications of \(x^2\) can provide insights into its significance in both theoretical and practical scenarios, highlighting its importance across various domains.
Practice Problems and Solutions
Here are some practice problems involving quadratic equations, along with detailed solutions to help you understand the steps involved in solving them.
Problem 1
Solve the quadratic equation \(x^2 - 4x - 5 = 0\).
Solution:
- Identify the coefficients: \(a = 1\), \(b = -4\), \(c = -5\).
- Set up the quadratic equation in standard form: \(ax^2 + bx + c = 0\).
- Factor the quadratic equation:
\(x^2 - 4x - 5 = (x - 5)(x + 1) = 0\).
- Set each factor equal to zero and solve for \(x\):
- \(x - 5 = 0 \Rightarrow x = 5\)
- \(x + 1 = 0 \Rightarrow x = -1\)
- The solutions are \(x = 5\) and \(x = -1\).
Problem 2
Solve the quadratic equation \(2x^2 + 3x - 2 = 0\).
Solution:
- Identify the coefficients: \(a = 2\), \(b = 3\), \(c = -2\).
- Set up the quadratic equation in standard form: \(ax^2 + bx + c = 0\).
- Use the quadratic formula: \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\).
- Calculate the discriminant: \(b^2 - 4ac = 3^2 - 4 \cdot 2 \cdot (-2) = 9 + 16 = 25\).
- Substitute the values into the quadratic formula:
\(x = \frac{-3 \pm \sqrt{25}}{4} = \frac{-3 \pm 5}{4}\).
- Simplify to find the two solutions:
- \(x = \frac{-3 + 5}{4} = \frac{2}{4} = \frac{1}{2}\)
- \(x = \frac{-3 - 5}{4} = \frac{-8}{4} = -2\)
- The solutions are \(x = \frac{1}{2}\) and \(x = -2\).
Problem 3
Solve the quadratic equation \(x^2 + 6x + 9 = 0\).
Solution:
- Identify the coefficients: \(a = 1\), \(b = 6\), \(c = 9\).
- Set up the quadratic equation in standard form: \(ax^2 + bx + c = 0\).
- Factor the quadratic equation:
\(x^2 + 6x + 9 = (x + 3)^2 = 0\).
- Set the factor equal to zero and solve for \(x\):
- \(x + 3 = 0 \Rightarrow x = -3\)
- The solution is \(x = -3\).
Practice Problems
Try solving the following problems on your own:
- Solve \(3x^2 - 2x - 1 = 0\).
- Solve \(x^2 + 2x - 8 = 0\).
- Solve \(4x^2 - 4x + 1 = 0\).
Once you have attempted the problems, check your solutions using the methods outlined above.
Conclusion
The concept of x squared, represented as \(x^2\), is a fundamental aspect of mathematics that extends beyond mere arithmetic. It plays a crucial role in various mathematical fields such as algebra, geometry, and calculus. Throughout this guide, we have explored the basic definition of \(x^2\), its properties, and its applications in solving quadratic equations, understanding parabolic graphs, and modeling real-world phenomena.
In the journey of understanding \(x^2\), we've discovered that:
- Basic Definition: \(x^2\) denotes a number or variable \(x\) multiplied by itself.
- Properties: It always results in a non-negative value for real numbers, influences the shape of quadratic graphs, and is essential in formulating and solving quadratic equations.
- Graphical Representation: The graph of a quadratic function \(y = x^2\) is a parabola that opens upwards.
- Quadratic Equations: These equations, of the form \(ax^2 + bx + c = 0\), can be solved using methods like factoring, completing the square, and the quadratic formula.
- Real-Life Applications: From physics (projectile motion) to engineering (structural analysis) and economics (cost functions), the concept of squaring numbers is integral to numerous practical applications.
Understanding and mastering the concept of \(x^2\) is a stepping stone to deeper mathematical comprehension and problem-solving abilities. As you continue to explore and practice, you will gain greater insights and appreciation for the elegance and utility of this fundamental mathematical principle. Remember, every mathematical challenge is an opportunity to enhance your skills and knowledge. Keep practicing, stay curious, and enjoy the journey of learning mathematics.
Hướng dẫn chi tiết cách giải phương trình x bình phương = 4 và các giá trị bình phương khác của x. Video này sẽ giúp bạn hiểu rõ hơn về các phương trình bậc hai và cách giải chúng.
Giải Phương Trình x Bình Phương = 4 và Các Giá Trị Bình Phương Khác của x
READ MORE:
Video của Corbettmaths hướng dẫn cách giải các phương trình x bình phương. Tìm hiểu cách tiếp cận và giải các bài toán liên quan đến x bình phương một cách dễ dàng.
Phương Trình x Bình Phương - Corbettmaths




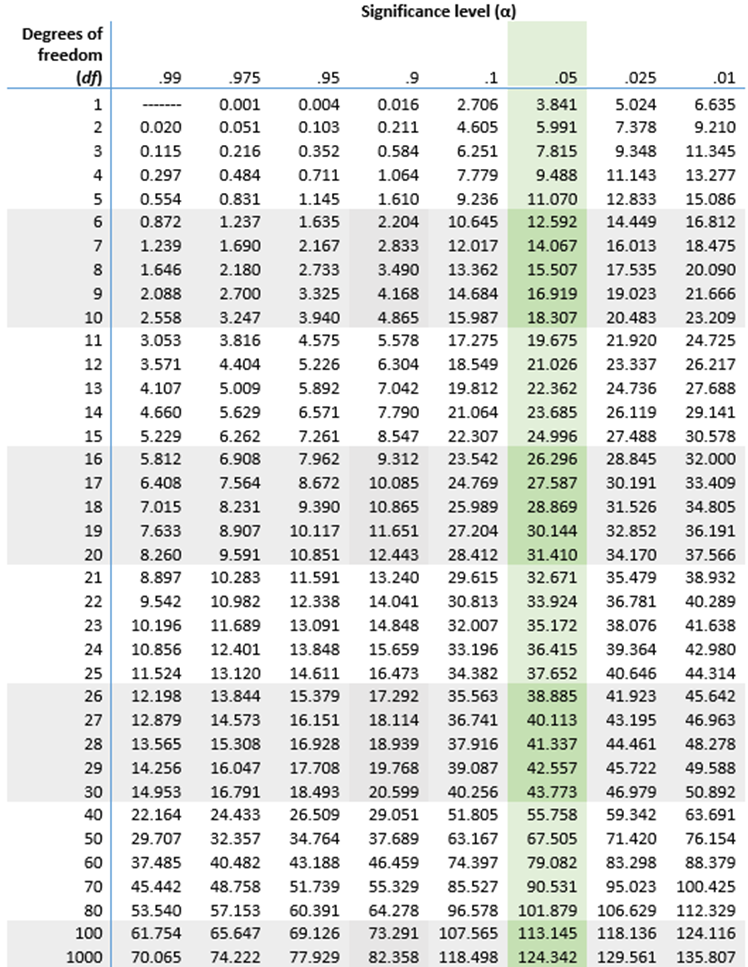
:max_bytes(150000):strip_icc()/Chi-SquareStatistic_Final_4199464-7eebcd71a4bf4d9ca1a88d278845e674.jpg)