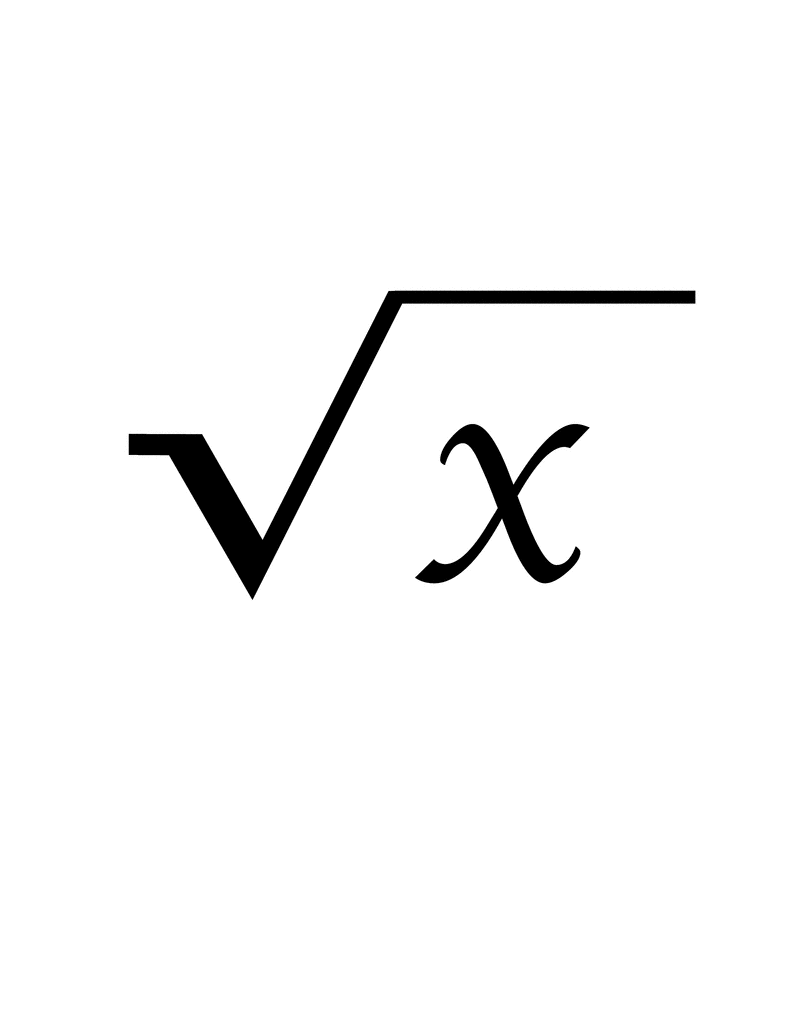Topic what is x-9 squared: Discover the simplicity and utility of the expression (x-9) squared. This guide delves into the methods of expanding and simplifying the expression, its significance in algebra, and its practical applications. Perfect for students and enthusiasts, learn how (x-9)^2 forms the basis for solving quadratic equations and understanding parabolic graphs.
Table of Content
- Understanding (x - 9)2
- Introduction to (x-9) Squared
- Basic Algebra Concepts
- Expanding (x-9)^2 Using FOIL Method
- Factoring Quadratic Expressions
- Simplification and Combining Like Terms
- Standard Form of (x-9)^2
- Using the Distributive Property
- Applications in Solving Quadratic Equations
- Graphical Representation of Quadratic Functions
- Real-world Examples and Practice Problems
- Interactive Tools and Calculators
- Conclusion and Further Resources
- YOUTUBE: Xử lý x^2 - 9 bằng công thức hiệu bình phương. Video này giải thích cách sử dụng công thức hiệu bình phương để phân tích đa thức và ứng dụng trong đề tài 'what is x-9 squared'?
Understanding (x - 9)2
To simplify the expression (x - 9)2, we need to expand it using algebraic methods. This involves applying the distributive property, also known as the FOIL method (First, Outer, Inner, Last).
Step-by-Step Simplification
- Rewrite the expression:
\((x - 9) (x - 9)\) - Apply the FOIL method to expand the expression:
- First: \(x \cdot x = x^2\)
- Outer: \(x \cdot (-9) = -9x\)
- Inner: \((-9) \cdot x = -9x\)
- Last: \((-9) \cdot (-9) = 81\)
- Combine like terms:
- \(x^2 - 9x - 9x + 81\)
Thus, the simplified form of \((x - 9)^2\) is \(x^2 - 18x + 81\).
Graphical Representation
When plotted on a graph, the function \(y = (x - 9)^2\) represents a parabola that opens upwards with its vertex at the point (9, 0).
Uses and Applications
This type of polynomial is commonly encountered in algebraic problems and has various applications in fields such as physics, engineering, and economics. Understanding how to expand and simplify such expressions is fundamental for solving quadratic equations and analyzing quadratic functions.
For further exploration and practice, consider using online tools such as:
READ MORE:
Introduction to (x-9) Squared
The expression \((x-9)^2\) represents a quadratic expression that can be expanded and simplified using algebraic techniques. Understanding this expression is fundamental in algebra, especially when dealing with polynomials and quadratic equations. Here's a step-by-step guide to understanding and working with \((x-9)^2\).
- Definition: The expression \((x-9)^2\) is read as "x minus nine squared" and represents the square of the binomial \(x-9\).
- Expansion: To expand \((x-9)^2\), we use the FOIL method (First, Outer, Inner, Last) as follows:
- First: \(x \cdot x = x^2\)
- Outer: \(x \cdot -9 = -9x\)
- Inner: \(-9 \cdot x = -9x\)
- Last: \(-9 \cdot -9 = 81\)
- Simplification: Combine like terms to simplify the expression:
\((x-9)^2 = x^2 - 9x - 9x + 81 = x^2 - 18x + 81\)
- Application: The simplified form \(x^2 - 18x + 81\) is useful in various algebraic contexts, including solving quadratic equations and graphing parabolas.
- Graphical Representation: When graphed, the quadratic equation \(y = (x-9)^2\) forms a parabola that opens upwards with its vertex at the point (9,0).
Understanding \((x-9)^2\) is crucial for mastering algebraic operations involving binomials and quadratics. By following the steps outlined above, students can confidently expand, simplify, and apply this expression in various mathematical problems.
Basic Algebra Concepts
Understanding basic algebra concepts is crucial for solving mathematical problems involving variables, expressions, and equations. Algebra provides the foundation for advanced mathematical studies and applications in various fields.
Here are some essential concepts in algebra:
- Variables: Symbols, usually letters, used to represent unknown values. For example, in the expression
\(x - 9\) , \(x\) is a variable. - Expressions: Combinations of variables, numbers, and operators. An example is
\(3x + 5\) . - Equations: Statements that assert the equality of two expressions, such as
\(2x + 3 = 7\) . - Operations: Basic arithmetic operations like addition, subtraction, multiplication, and division. In algebra, these operations are applied to variables and expressions.
- Distributive Property: A property that states
\(a(b + c) = ab + ac\) . This is used to expand expressions.
In solving algebraic problems, you often need to simplify expressions, solve for variables, and apply properties like the distributive property. For example, to simplify
- Expand using the FOIL method:
\((x-9)(x-9) = x^2 - 9x - 9x + 81\) . - Combine like terms:
\(x^2 - 18x + 81\) .
These steps illustrate the process of simplifying an expression, a fundamental skill in algebra.
Expanding (x-9)^2 Using FOIL Method
To expand \((x-9)^2\) using the FOIL method, we follow a systematic process. FOIL stands for First, Outer, Inner, and Last, which are the terms we multiply in the binomials.
- First: Multiply the first terms in each binomial.
\((x-9)(x-9)\)
\(x \cdot x = x^2\)
- Outer: Multiply the outer terms in each binomial.
\((x-9)(x-9)\)
\(x \cdot (-9) = -9x\)
- Inner: Multiply the inner terms in each binomial.
\((x-9)(x-9)\)
\(-9 \cdot x = -9x\)
- Last: Multiply the last terms in each binomial.
\((x-9)(x-9)\)
\(-9 \cdot (-9) = 81\)
Combining these results, we get:
\(x^2 - 9x - 9x + 81\)
Simplifying further, we combine like terms:
\(x^2 - 18x + 81\)
Thus, the expanded form of \((x-9)^2\) is:
\(x^2 - 18x + 81\)
Factoring Quadratic Expressions
Factoring quadratic expressions is an essential skill in algebra. It involves rewriting a quadratic expression in the form \(ax^2 + bx + c\) as a product of two binomials. The steps to factor a quadratic expression are as follows:
- Identify a, b, and c: In the quadratic expression \(ax^2 + bx + c\), identify the coefficients a, b, and c. For example, in \(x^2 - 18x + 81\), \(a = 1\), \(b = -18\), and \(c = 81\).
- Find two numbers that multiply to ac and add to b: Look for two numbers whose product is \(ac\) (in this case, \(1 \cdot 81 = 81\)) and whose sum is \(b\) (which is \(-18\)). The numbers \(-9\) and \(-9\) satisfy these conditions.
- Rewrite the middle term using these numbers: Rewrite \(-18x\) as \(-9x - 9x\). The expression becomes \(x^2 - 9x - 9x + 81\).
- Factor by grouping: Group the terms to factor by grouping:
- \(x^2 - 9x - 9x + 81\)
- \((x^2 - 9x) + (-9x + 81)\)
- Factor out the common factor in each group:
- \(x(x - 9) - 9(x - 9)\)
- Factor out the common binomial factor: The expression becomes:
- \((x - 9)(x - 9)\)
Thus, the factored form of \(x^2 - 18x + 81\) is \((x - 9)^2\). This method of factoring quadratics by grouping is a powerful technique for solving quadratic equations and simplifying expressions.

Simplification and Combining Like Terms
The process of simplifying and combining like terms is essential in algebra. This step helps to make expressions more manageable and to find solutions efficiently. Here, we will look at how to simplify and combine like terms using the expression .
- Expand the Expression:
Start by expanding the expression using the distributive property:
Using the distributive property (FOIL method):
- First:
- Outer:
- Inner:
- Last:
- Combine Like Terms:
After expansion, combine the like terms:
Combine the terms:
- Simplify:
The simplified form of the expression is:
Standard Form of (x-9)^2
The standard form of the expression (x-9)^2 is crucial in algebraic manipulation and understanding quadratic equations. This form is known as the square of a binomial and can be expanded using the FOIL method, which stands for First, Outer, Inner, Last.
To expand (x-9)^2, apply the FOIL method:
| First: | x * x = x^2 |
| Outer: | x * (-9) = -9x |
| Inner: | -9 * x = -9x |
| Last: | -9 * (-9) = 81 |
Combine all these results to obtain the expanded form:
(x - 9)^2 = x^2 - 18x + 81
This expanded form, x^2 - 18x + 81, represents a quadratic expression in standard form, ax^2 + bx + c, where a = 1, b = -18, and c = 81. It is useful for solving quadratic equations, graphing quadratic functions, and understanding the symmetry properties of the parabola.
Using the Distributive Property
When dealing with the expression (x-9)^2, applying the distributive property is essential for expanding it correctly. The distributive property allows us to distribute each term inside the parentheses to every term inside the parentheses.
Let's expand (x-9)^2 step by step using the distributive property:
| (x-9)^2 = (x-9) * (x-9) |
| = x * (x-9) - 9 * (x-9) |
| = x^2 - 9x - 9x + 81 |
| = x^2 - 18x + 81 |
Thus, using the distributive property correctly yields the expanded form of (x-9)^2 as x^2 - 18x + 81, which is crucial in algebraic manipulation and solving quadratic equations.
Applications in Solving Quadratic Equations
The expression (x-9)^2, when expanded to x^2 - 18x + 81, is directly applicable in solving quadratic equations. Quadratic equations are equations of the form ax^2 + bx + c = 0, where a, b, and c are constants and x is the variable.
To demonstrate its application, consider the following quadratic equation:
x^2 - 18x + 81 = 0
This equation can be solved using various methods such as factoring, completing the square, or using the quadratic formula. Here, the expanded form of (x-9)^2 helps in identifying the coefficients of x^2, x, and the constant term, which are crucial for solving the equation.
By applying appropriate methods to solve quadratic equations derived from expressions like (x-9)^2, one can find the solutions that satisfy the equation and interpret the results in real-world scenarios involving quadratic relationships.

Graphical Representation of Quadratic Functions
Quadratic functions, represented by equations like y = ax^2 + bx + c, where a, b, and c are constants, have distinctive graphical representations called parabolas. These graphs are symmetric and either open upwards (when a > 0) or downwards (when a < 0).
The quadratic function derived from (x-9)^2, which is x^2 - 18x + 81, can be graphically represented as:
- The graph is a parabola that opens upwards since the coefficient of x^2 (a) is positive (a = 1).
- The vertex of the parabola, determined by the formula x = -b/(2a), helps locate the minimum point of the graph.
- The x-intercepts (roots) of the quadratic function correspond to the solutions of the equation x^2 - 18x + 81 = 0, found using methods such as factoring or the quadratic formula.
- Understanding the graphical representation of quadratic functions is essential for interpreting real-world scenarios such as projectile motion, optimization problems, and engineering applications.
Real-world Examples and Practice Problems
Understanding the expression (x-9)^2 and its expanded form x^2 - 18x + 81 has practical applications in various real-world scenarios and provides opportunities for practice in solving related problems.
Here are some examples and practice problems involving (x-9)^2:
- A manufacturer wants to determine the minimum cost of production represented by the function C(x) = x^2 - 18x + 81, where x is the number of units produced and C(x) is the total cost. What is the production level that minimizes cost?
- An architect needs to design a parabolic arch for a bridge using the equation y = x^2 - 18x + 81, where y represents the height of the arch and x is the horizontal distance. What are the dimensions of the arch to achieve the desired height?
- A physics student investigates the trajectory of a ball launched from a height of 81 meters with an initial velocity that forms a parabolic path described by (x-9)^2. What is the maximum height reached by the ball?
These examples illustrate how (x-9)^2 can be applied to solve real-world problems involving optimization, design, and physics, enhancing understanding and proficiency in quadratic equations and their graphical representations.
Interactive Tools and Calculators
Interactive tools and calculators can greatly assist in exploring and understanding the expression (x-9)^2 and its applications in algebra and quadratic equations.
Here are some functionalities that interactive tools can provide:
- Expression Evaluation: Enter different values of x to instantly compute (x-9)^2 and visualize its expanded form x^2 - 18x + 81.
- Graphing Utility: Plot the graph of the quadratic function y = x^2 - 18x + 81 to observe the parabolic shape and its key characteristics such as vertex, roots, and axis of symmetry.
- Solving Quadratic Equations: Input quadratic equations derived from (x-9)^2 and use the calculator to solve for roots, facilitating understanding of how the equation relates to real-world scenarios.
- Interactive Examples: Explore interactive examples and practice problems related to (x-9)^2, with step-by-step solutions provided for deeper comprehension.
By utilizing interactive tools and calculators, learners can engage actively with (x-9)^2, reinforce algebraic skills, and gain insights into its practical applications in various fields.
Conclusion and Further Resources
In conclusion, understanding (x-9)^2 and its expanded form x^2 - 18x + 81 is fundamental in algebraic manipulation, quadratic equations, and graphical representations of quadratic functions.
Key takeaways include:
- The expression (x-9)^2 can be expanded using methods like FOIL or the distributive property to obtain x^2 - 18x + 81.
- Graphically, the quadratic function y = x^2 - 18x + 81 forms a parabola that opens upwards with vertex (9, 81).
- Applications of (x-9)^2 include solving optimization problems, understanding projectile motion, and designing structures with parabolic shapes.
For further exploration, here are some resources:
- Textbooks on algebra and quadratic equations for in-depth study.
- Online courses and tutorials offering interactive lessons on quadratic functions and their applications.
- Graphing calculators and software for visualizing and solving quadratic equations.
Continued practice and exploration of (x-9)^2 and related topics will enhance proficiency in algebra and deepen understanding of quadratic relationships in mathematics and beyond.

Xử lý x^2 - 9 bằng công thức hiệu bình phương. Video này giải thích cách sử dụng công thức hiệu bình phương để phân tích đa thức và ứng dụng trong đề tài 'what is x-9 squared'?
Factor x^2 - 9 using the Difference of Squares Formula
READ MORE:
Video này hướng dẫn giải phương trình x^2-9=0 bằng hai phương pháp khác nhau.
Giải phương trình x^2-9=0 (Hai phương pháp)