Topic square root of 225 simplified: Discover how to simplify the square root of 225 with easy steps and clear explanations. This guide will walk you through the process, ensuring you understand the prime factorization method and how to verify your results. Perfect for students, teachers, and math enthusiasts looking to deepen their knowledge of square roots.
Table of Content
- Square Root of 225 Simplified
- Introduction to Square Roots
- Definition and Properties of Square Roots
- Prime Factorization Method
- Calculating the Square Root of 225
- Verification of the Square Root Calculation
- Common Mistakes in Simplifying Square Roots
- Practical Applications of Square Roots
- Frequently Asked Questions
- YOUTUBE: Hướng dẫn tìm căn bậc hai của 225 bằng phương pháp phân tích nhân tử nguyên tố. Video giải thích cách tính căn bậc hai một cách đơn giản và dễ hiểu.
Square Root of 225 Simplified
The square root of a number is a value that, when multiplied by itself, gives the original number. For the number 225, the simplified square root can be determined as follows:
Calculation
We start by finding the prime factors of 225.
- 225 can be factored into 15 × 15.
- Each 15 can be further factored into 3 × 5.
Thus, the prime factorization of 225 is:
\[ 225 = 3^2 \times 5^2 \]
Taking the square root of both sides, we get:
\[ \sqrt{225} = \sqrt{3^2 \times 5^2} \]
Using the property of square roots that \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\), we can simplify this to:
\[ \sqrt{225} = \sqrt{3^2} \times \sqrt{5^2} \]
Since the square root of a square number is the base of the exponent, we find:
\[ \sqrt{3^2} = 3 \]
\[ \sqrt{5^2} = 5 \]
Therefore:
\[ \sqrt{225} = 3 \times 5 = 15 \]
Conclusion
The simplified square root of 225 is:
\[ \sqrt{225} = 15 \]
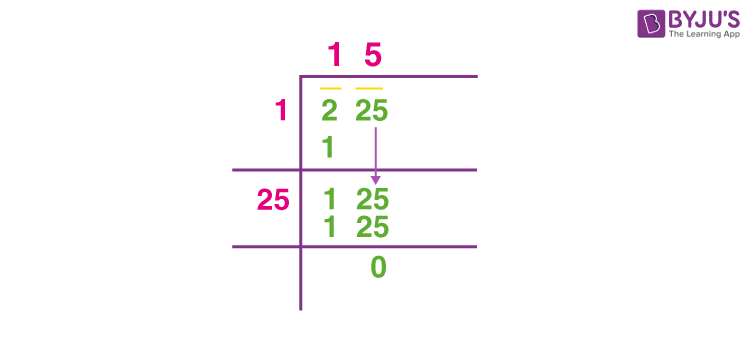
READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical operations that are essential in various fields of study, including algebra, geometry, and calculus. The square root of a number is a value that, when multiplied by itself, gives the original number. Understanding square roots is crucial for solving quadratic equations, working with exponential functions, and simplifying radicals.
Here are some key points to understand about square roots:
- The square root of a number \( x \) is denoted as \( \sqrt{x} \).
- For any positive number \( x \), \( \sqrt{x} \) is a real number.
- The square root of a perfect square is always an integer. For example, \( \sqrt{16} = 4 \) because \( 4 \times 4 = 16 \).
To further illustrate, let's break down the process of finding the square root of a specific number, such as 225. We will use the prime factorization method:
- First, factorize 225 into its prime components: \( 225 = 15 \times 15 \).
- Next, factor each 15 into prime factors: \( 15 = 3 \times 5 \). Therefore, \( 225 = (3 \times 5) \times (3 \times 5) = 3^2 \times 5^2 \).
- Take the square root of both sides: \( \sqrt{225} = \sqrt{3^2 \times 5^2} = \sqrt{3^2} \times \sqrt{5^2} = 3 \times 5 = 15 \).
This method shows that the square root of 225 simplifies to 15. By understanding these fundamental steps, you can apply the same principles to simplify the square roots of other perfect squares.
Definition and Properties of Square Roots
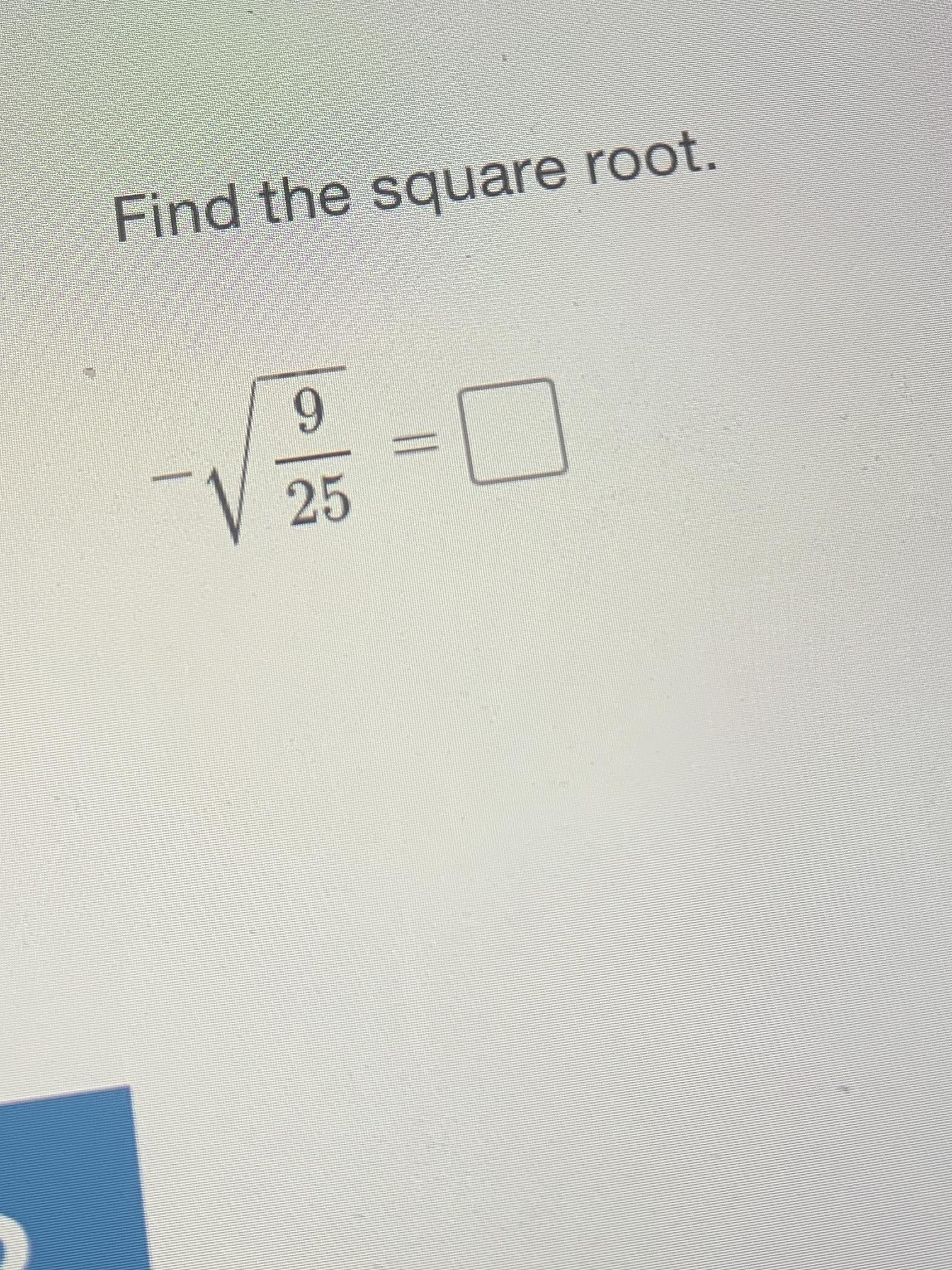
The square root of a number is a value that, when multiplied by itself, results in the original number. It is denoted by the radical symbol \( \sqrt{} \). For example, the square root of 225 is written as \( \sqrt{225} \).
Here are some fundamental properties of square roots:
- Non-negative results: The square root of a non-negative number is also non-negative. For instance, \( \sqrt{225} = 15 \).
- Product property: The square root of a product is the product of the square roots of the factors. Mathematically, \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). For example, \( \sqrt{225} = \sqrt{15 \times 15} = \sqrt{15} \times \sqrt{15} \).
- Quotient property: The square root of a quotient is the quotient of the square roots of the numerator and the denominator. Mathematically, \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \) for \( b \neq 0 \).
- Square of the square root: The square of the square root of a number returns the original number. Mathematically, \( (\sqrt{a})^2 = a \). For example, \( (\sqrt{225})^2 = 225 \).
- Perfect squares: The square root of a perfect square is always an integer. For example, \( \sqrt{225} = 15 \) because \( 15 \times 15 = 225 \).
- Irrational numbers: The square root of a non-perfect square is an irrational number. For example, \( \sqrt{2} \) is an irrational number because it cannot be expressed as a simple fraction.
Understanding these properties helps in simplifying expressions and solving equations involving square roots. Let's look at the specific example of 225:
- Factorize 225 into its prime factors: \( 225 = 15 \times 15 \).
- Further factorize 15 into prime factors: \( 15 = 3 \times 5 \). Thus, \( 225 = (3 \times 5) \times (3 \times 5) = 3^2 \times 5^2 \).
- Apply the product property: \( \sqrt{225} = \sqrt{3^2 \times 5^2} = \sqrt{3^2} \times \sqrt{5^2} \).
- Simplify the square roots of the factors: \( \sqrt{3^2} = 3 \) and \( \sqrt{5^2} = 5 \).
- Multiply the results: \( 3 \times 5 = 15 \).
Thus, the square root of 225 is 15, which demonstrates the application of the properties of square roots.
Prime Factorization Method
The prime factorization method is a systematic way of determining the square root of a number by breaking it down into its prime factors. Follow these steps to find the square root of 225 using the prime factorization method:
-
Start by finding the prime factors of 225. Begin with the smallest prime number, which is 2, and continue with higher prime numbers until the number is fully factorized.
Since 225 is an odd number, it is not divisible by 2. The next smallest prime number is 3:
- \(225 \div 3 = 75\)
- \(75 \div 3 = 25\)
- \(25 \div 5 = 5\)
- \(5 \div 5 = 1\)
-
Write down the prime factors obtained from the division:
\(225 = 3 \times 3 \times 5 \times 5\)
-
Group the prime factors into pairs of identical numbers:
\(225 = (3 \times 3) \times (5 \times 5)\)
-
Take the square root of each pair of identical numbers:
\(\sqrt{225} = \sqrt{(3 \times 3) \times (5 \times 5)} = 3 \times 5\)
-
Multiply the results to get the simplified square root:
\(\sqrt{225} = 15\)
Therefore, the square root of 225 is 15. The prime factorization method helps us simplify the process by breaking down the number into its basic building blocks and recombining them in a straightforward manner.
Calculating the Square Root of 225
To calculate the square root of 225, we can use various methods. Below are detailed steps for three common methods: Prime Factorization, Long Division, and Repeated Subtraction.
Prime Factorization Method
The prime factorization method involves breaking down 225 into its prime factors.
- First, write the prime factors of 225:
\(225 = 3 \times 3 \times 5 \times 5\)
- Next, group the prime factors into pairs:
\(225 = (3 \times 3) \times (5 \times 5)\)
- Take the square root of each pair:
\(\sqrt{225} = \sqrt{(3 \times 3) \times (5 \times 5)} = 3 \times 5 = 15\)
Therefore, the square root of 225 is 15.
Long Division Method
The long division method involves dividing the number step-by-step.
- Set up the number 225 for long division:
15 | 2 25
1
-1
1 25
2 5
-1 25
0
- Find the largest number whose square is less than or equal to 225, which is 15.
- Thus, the square root of 225 is 15.
Repeated Subtraction Method
The repeated subtraction method involves subtracting successive odd numbers from 225 until we reach zero.
- Start with 225 and subtract successive odd numbers:
- 225 - 1 = 224
- 224 - 3 = 221
- 221 - 5 = 216
- 216 - 7 = 209
- 209 - 9 = 200
- 200 - 11 = 189
- 189 - 13 = 176
- 176 - 15 = 161
- 161 - 17 = 144
- 144 - 19 = 125
- 125 - 21 = 104
- 104 - 23 = 81
- 81 - 25 = 56
- 56 - 27 = 29
- 29 - 29 = 0
- Since we subtracted 15 times to reach zero, the square root of 225 is 15.
Using any of these methods, we find that the square root of 225 is 15.

Verification of the Square Root Calculation
To verify the calculation of the square root of 225, we can use several methods. The most straightforward method is to square the result and see if we get the original number back. For the square root of 225, we calculated it as 15. Let's verify this step by step:
Verification by Squaring the Result
If the square root of 225 is 15, then squaring 15 should give us 225.
\[
15^2 = 15 \times 15 = 225
\]
Since squaring 15 gives us 225, our calculation is verified.
Verification Using Prime Factorization
Another method to verify the square root calculation is through prime factorization:
- Prime factorize 225: \[ 225 = 3^2 \times 5^2 \]
- Take the square root of the prime factors: \[ \sqrt{225} = \sqrt{3^2 \times 5^2} \]
- Since the square root of a product is the product of the square roots: \[ \sqrt{3^2} \times \sqrt{5^2} = 3 \times 5 = 15 \]
This confirms that the square root of 225 is indeed 15.
Verification Using the Long Division Method
The long division method is a systematic way to find the square root of a number. Here’s how it works for 225:
- Write 225 under the long division symbol.
- Pair the digits from right to left: 2 | 25.
- Find the largest number whose square is less than or equal to 2. This number is 1.
- Place 1 above the division bar and subtract its square (1) from 2 to get the remainder 1.
- Bring down the next pair of digits (25) to make the new dividend 125.
- Double the quotient (1) to get the new divisor's first digit (2). Find the number X such that 2X times X is less than or equal to 125. X is 5.
- Place 5 next to 1 on top (making 15) and subtract 125 (25 × 5) from 125 to get the remainder 0.
Since the remainder is 0, the quotient 15 is confirmed as the square root of 225.
By these methods, we have verified that the square root of 225 is indeed 15.
Common Mistakes in Simplifying Square Roots
When simplifying square roots, there are several common mistakes that learners often make. Understanding these errors can help avoid them and ensure accurate simplification.
- Forgetting to Check for Perfect Squares:
One of the most frequent mistakes is neglecting to identify perfect square factors of the radicand (the number under the square root). For instance, in simplifying \( \sqrt{225} \), recognizing that \( 225 \) is a perfect square (since \( 15^2 = 225 \)) simplifies the process greatly.
- Incorrectly Simplifying Non-Perfect Squares:
Another common error is simplifying a square root without proper factorization. For example, \( \sqrt{72} \) should be simplified by recognizing \( 72 = 36 \times 2 \). Thus, \( \sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2} \).
- Overlooking Pairs in Prime Factorization:
When using prime factorization, it is important to correctly pair factors. For example, for \( \sqrt{50} \), the prime factors are \( 2 \) and \( 5 \times 5 \). This means \( \sqrt{50} = \sqrt{2 \times 25} = \sqrt{2} \times \sqrt{25} = 5\sqrt{2} \). Missing such pairs can lead to incorrect simplifications.
- Not Simplifying Completely:
Sometimes, the simplification process is not carried out to its fullest extent. For instance, in simplifying \( \sqrt{180} \), it should be broken down as \( \sqrt{36 \times 5} = 6\sqrt{5} \). Stopping at \( \sqrt{9 \times 20} = 3\sqrt{20} \) leaves further simplification to be desired.
- Confusing Radicands and Results:
Ensure the radicand remains consistent during simplification. Mistakes can occur if intermediate steps are incorrectly combined. For instance, mishandling \( \sqrt{48} \) can lead to errors if not properly simplified to \( 4\sqrt{3} \).
By recognizing and avoiding these common mistakes, the process of simplifying square roots becomes more straightforward and accurate.
Practical Applications of Square Roots
Square roots have numerous practical applications across various fields. Here are some of the key areas where square roots play an essential role:
-
Finance:
In finance, square roots are used to calculate stock market volatility. The volatility is measured by taking the variance of stock returns and then finding the square root, which helps investors assess the risk associated with different investments.
-
Architecture:
Square roots are crucial in engineering and architecture to determine the natural frequency of structures like bridges and buildings. This helps in predicting how a structure will respond to various loads, such as wind or traffic.
-
Science:
Many scientific calculations involve square roots, such as determining the velocity of a moving object, the absorption of radiation by materials, and the intensity of sound waves. These calculations help scientists understand natural phenomena and develop new technologies.
-
Statistics:
Square roots are used in statistical analysis to calculate standard deviation, which is the square root of the variance. This measure helps in understanding how data points deviate from the mean, providing insights into the data's spread and consistency.
-
Geometry:
In geometry, square roots are used to calculate the area and perimeter of shapes and solve problems involving right triangles. The Pythagorean theorem, for instance, involves square roots to determine the length of the hypotenuse.
-
Computer Science:
Square roots are used in computer programming for encryption algorithms, image processing, and game physics. For example, encryption algorithms use square roots to generate secure keys for data protection.
-
Navigation:
Square roots are applied in navigation to compute distances between points on a map or globe and to estimate directions. Pilots and sailors use these calculations to determine the most efficient routes.
-
Electrical Engineering:
In electrical engineering, square roots are used to calculate power, voltage, and current in circuits, which is vital for designing and optimizing electrical systems.
-
Photography:
The aperture of a camera lens is described by an f-number, which is related to the square root of the area of the aperture. This affects the amount of light entering the camera and influences exposure settings.
-
Telecommunication:
Square roots are used in telecommunications to describe the inverse square law, which explains how signal strength decreases with distance. This is important for designing efficient communication systems.
These examples illustrate how square roots are integral to solving practical problems in various disciplines, highlighting their importance in everyday applications and advanced technological developments.
Frequently Asked Questions
-
What is the square root of 225?
The square root of 225 is 15. This is because \( 15 \times 15 = 225 \).
-
Is 225 a perfect square?
Yes, 225 is a perfect square because its square root is a whole number, 15.
-
How do you simplify the square root of 225?
The square root of 225 is already in its simplest form, which is 15.
-
Can the square root of 225 be negative?
Yes, technically the square root of 225 can be both positive and negative. Thus, \( \sqrt{225} = \pm 15 \). However, the principal square root is the positive value.
-
How do you calculate the square root of 225 using a calculator?
To find the square root of 225 using a calculator, simply enter 225 and press the square root (√) button. The result will be 15.
-
What is the prime factorization method for finding the square root of 225?
The prime factorization of 225 is \( 3^2 \times 5^2 \). Taking the square root of each factor and multiplying them gives \( 3 \times 5 = 15 \).
-
Is the square root of 225 a rational number?
Yes, the square root of 225 is a rational number because it can be expressed as the fraction \(\frac{15}{1}\).
-
What are some practical applications of square roots?
Square roots are used in various fields such as geometry, physics, engineering, and computer science. They help in calculating areas, solving quadratic equations, and analyzing signal processing among other applications.

Hướng dẫn tìm căn bậc hai của 225 bằng phương pháp phân tích nhân tử nguyên tố. Video giải thích cách tính căn bậc hai một cách đơn giản và dễ hiểu.
Làm thế nào để Tìm Căn bậc hai của 225 bằng Phân tích Nhân tử Nguyên tố / Căn bậc hai của 225 / Căn bậc hai 225
READ MORE:
Hướng dẫn cách tìm căn bậc hai của 225 mà không cần sử dụng máy tính. Video giải thích chi tiết từng bước để tính căn bậc hai một cách dễ hiểu và trực quan.
Tìm căn bậc hai của 225 mà không sử dụng máy tính