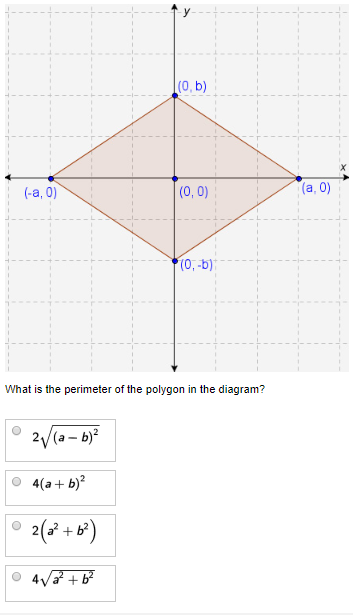
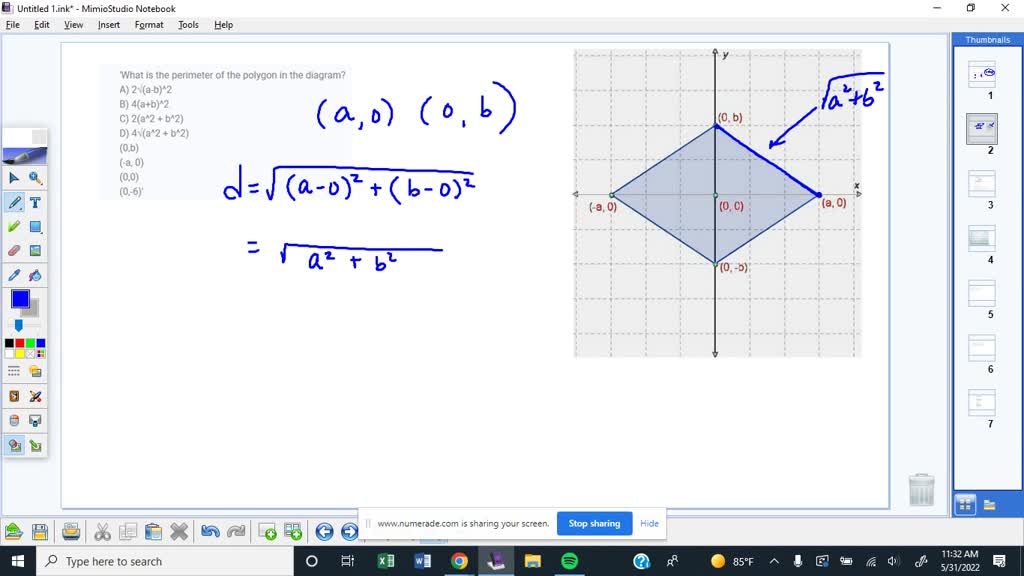
Topic what is the perimeter of the polygon in the diagram: Discover how to calculate the perimeter of the polygon in the diagram with our easy-to-follow guide. Learn the essential formulas and methods for both regular and irregular polygons, and master perimeter calculations in no time. This article will help you understand the concepts clearly and apply them effectively in various scenarios.
Table of Content
- Perimeter of a Polygon
- Introduction to Polygons
- Definition of Perimeter
- Types of Polygons
- Regular vs. Irregular Polygons
- Calculating the Perimeter of Regular Polygons
- Examples of Regular Polygon Perimeter Calculation
- Calculating the Perimeter of Irregular Polygons
- Methods for Irregular Polygon Perimeter Calculation
- Examples of Irregular Polygon Perimeter Calculation
- Practical Applications of Perimeter Calculation
- Common Mistakes and Tips
- Advanced Topics in Perimeter Calculation
- Perimeter in Coordinate Geometry
- Using Technology for Perimeter Calculation
- Conclusion and Summary
- Additional Resources
- Frequently Asked Questions
- YOUTUBE: Chu vi của một đa giác
Perimeter of a Polygon
The perimeter of a polygon is the total length of its boundary, calculated by summing the lengths of all its sides. Polygons can be regular or irregular, each with specific methods to find their perimeter.
Definition
A polygon is a 2-dimensional shape with straight sides, and its perimeter is the sum of the lengths of these sides. The formula to find the perimeter is straightforward:
\[
\text{Perimeter} = \sum_{i=1}^{n} \text{side}_i
\]
Steps to Calculate the Perimeter
- Identify and measure the lengths of all sides of the polygon.
- Ensure all side lengths are in the same unit.
- Sum the lengths of all sides to get the perimeter.
Formula for Regular Polygons
For regular polygons, where all sides and angles are equal:
\[
\text{Perimeter} = n \times s
\]
where \( n \) is the number of sides, and \( s \) is the length of one side.
Examples
Example 1: Regular Polygon
Consider a regular pentagon with each side length of 6 cm:
\[
\text{Perimeter} = 5 \times 6 = 30 \, \text{cm}
\]
Example 2: Irregular Polygon
Consider an irregular hexagon with side lengths 9 cm, 2 cm, 6 cm, 10 cm, 3 cm, and 12 cm:
\[
\text{Perimeter} = 9 + 2 + 6 + 10 + 3 + 12 = 42 \, \text{cm}
\]
Conclusion
The concept of the perimeter is crucial in various mathematical and practical applications. Whether dealing with regular or irregular polygons, the process involves summing the lengths of all sides, which is essential for understanding and solving geometric problems.

READ MORE:
Introduction to Polygons
A polygon is a two-dimensional geometric figure with a finite number of straight line segments connected to form a closed shape. These segments are called sides or edges, and the points where two edges meet are called vertices or corners. Polygons are named based on the number of sides they have.
Here are some common types of polygons based on the number of sides:
- Triangle: 3 sides
- Quadrilateral: 4 sides
- Pentagon: 5 sides
- Hexagon: 6 sides
- Heptagon: 7 sides
- Octagon: 8 sides
- Nonagon: 9 sides
- Decagon: 10 sides
Polygons can be classified into two main types: regular and irregular polygons. A regular polygon has all sides and angles equal, whereas an irregular polygon has sides and angles of different lengths and degrees.
The perimeter of a polygon is the total distance around the outside, which can be calculated by adding the lengths of all its sides. For a regular polygon with \( n \) sides of length \( s \), the perimeter \( P \) is given by:
\[
P = n \times s
\]
For irregular polygons, the perimeter is calculated by summing the lengths of each side:
\[
P = s_1 + s_2 + s_3 + \ldots + s_n
\]
Understanding the properties and classification of polygons is fundamental for calculating their perimeter and applying these concepts in various mathematical and real-world scenarios.
Definition of Perimeter
The perimeter of a polygon is defined as the total length of all its sides. It represents the distance around the boundary of the polygon. The perimeter is an important measurement in geometry, providing essential information for various applications such as construction, design, and land measurement.
To understand the concept of perimeter, consider the following points:
- Simple Definition: The perimeter is the sum of the lengths of all the sides of a polygon.
- Units of Measurement: Perimeter is measured in linear units such as meters, centimeters, inches, or feet, depending on the context.
The formula for calculating the perimeter varies based on the type of polygon:
1. Perimeter of Regular Polygons:
For a regular polygon (a polygon with all sides and angles equal), the perimeter \( P \) can be calculated using the formula:
\[
P = n \times s
\]
where \( n \) is the number of sides and \( s \) is the length of each side.
For example, the perimeter of a regular hexagon (6 sides) with each side measuring 4 units is:
\[
P = 6 \times 4 = 24 \text{ units}
\]
2. Perimeter of Irregular Polygons:
For an irregular polygon (a polygon with sides and angles of different lengths and degrees), the perimeter is the sum of the lengths of all sides:
\[
P = s_1 + s_2 + s_3 + \ldots + s_n
\]
where \( s_1, s_2, s_3, \ldots, s_n \) are the lengths of the sides.
For example, the perimeter of an irregular pentagon with sides measuring 3, 4, 5, 6, and 7 units is:
\[
P = 3 + 4 + 5 + 6 + 7 = 25 \text{ units}
\]
Understanding the definition and calculation of perimeter is fundamental for solving various geometric problems and is widely applicable in real-world contexts.
Types of Polygons
Polygons are classified based on various characteristics, such as the number of sides, the lengths of the sides, and the measures of the angles. Understanding these classifications helps in identifying and working with different polygons effectively.
Here are the main types of polygons:
- Based on the Number of Sides:
- Triangle: A polygon with 3 sides.
- Quadrilateral: A polygon with 4 sides.
- Pentagon: A polygon with 5 sides.
- Hexagon: A polygon with 6 sides.
- Heptagon: A polygon with 7 sides.
- Octagon: A polygon with 8 sides.
- Nonagon: A polygon with 9 sides.
- Decagon: A polygon with 10 sides.
- Based on the Regularity of Sides and Angles:
- Regular Polygon: All sides and angles are equal. Examples include the equilateral triangle and the square.
- Irregular Polygon: Sides and angles are of different lengths and measures. An example is a scalene triangle.
- Based on Convexity:
- Convex Polygon: All interior angles are less than 180 degrees, and no sides are indented. Examples include regular polygons like the hexagon.
- Concave Polygon: At least one interior angle is greater than 180 degrees, and some sides may be indented. An example is a star-shaped polygon.
- Special Types of Quadrilaterals:
- Square: A regular quadrilateral with all sides and angles equal.
- Rectangle: Opposite sides are equal, and all angles are 90 degrees.
- Rhombus: All sides are equal, but angles are not 90 degrees.
- Parallelogram: Opposite sides are parallel and equal, but angles are not 90 degrees.
- Trapezoid: Only one pair of opposite sides is parallel.
Understanding the types of polygons is essential for calculating their perimeters, as different types have different properties and formulas associated with them. This knowledge also aids in various mathematical applications and problem-solving scenarios.
Regular vs. Irregular Polygons
Polygons can be classified into two main categories based on the equality of their sides and angles: regular and irregular polygons. Understanding the differences between these two types is crucial for geometric calculations and applications.
Regular Polygons:
A regular polygon has all sides of equal length and all interior angles of equal measure. This symmetry makes regular polygons simpler to analyze and work with in various geometric contexts. The following are key characteristics of regular polygons:
- All sides are equal: Each side has the same length.
- All angles are equal: Each interior angle has the same measure.
- High degree of symmetry: Regular polygons are highly symmetrical.
- Simpler perimeter calculation: The perimeter \( P \) can be easily calculated using the formula: \[ P = n \times s \] where \( n \) is the number of sides and \( s \) is the length of each side.
Examples of regular polygons include the equilateral triangle (3 equal sides), the square (4 equal sides), and the regular hexagon (6 equal sides).
Irregular Polygons:
An irregular polygon has sides and angles of different lengths and measures. Unlike regular polygons, irregular polygons do not have uniform symmetry, making their analysis more complex. Key characteristics of irregular polygons include:
- Sides of different lengths: Each side can have a unique length.
- Angles of different measures: Each interior angle can have a different measure.
- Less symmetry: Irregular polygons lack the symmetry found in regular polygons.
- Complex perimeter calculation: The perimeter \( P \) is calculated by summing the lengths of all sides: \[ P = s_1 + s_2 + s_3 + \ldots + s_n \] where \( s_1, s_2, s_3, \ldots, s_n \) are the lengths of the sides.
Examples of irregular polygons include scalene triangles (triangles with sides of different lengths) and irregular quadrilaterals (four-sided polygons with sides and angles of varying lengths and measures).
In summary, regular polygons are characterized by their equal sides and angles, which simplify many geometric calculations. Irregular polygons, with their varying side lengths and angle measures, require more detailed analysis for accurate calculations. Understanding these differences is fundamental for effectively working with different types of polygons.

Calculating the Perimeter of Regular Polygons
Calculating the perimeter of a regular polygon is straightforward due to its symmetrical properties. A regular polygon has all sides of equal length and all interior angles of equal measure. The formula to calculate the perimeter is simple and efficient.
Here are the steps to calculate the perimeter of a regular polygon:
- Identify the number of sides: Determine the number of sides \( n \) of the polygon. For example, a hexagon has 6 sides.
- Measure the length of one side: Measure or obtain the length \( s \) of one side of the polygon. For example, if one side of a hexagon is 5 units long, then \( s = 5 \) units.
- Use the perimeter formula: The formula to calculate the perimeter \( P \) of a regular polygon is: \[ P = n \times s \] where \( n \) is the number of sides and \( s \) is the length of each side.
Let's go through an example:
- Example: Calculate the perimeter of a regular pentagon with each side measuring 4 units.
- Number of sides \( n \) = 5
- Length of one side \( s \) = 4 units
- Perimeter \( P \) = \( n \times s \) = \( 5 \times 4 \) = 20 units
Using this formula, you can quickly find the perimeter of any regular polygon as long as you know the number of sides and the length of one side. This method is efficient and avoids the need for more complex calculations required for irregular polygons.
Regular polygons include shapes like equilateral triangles, squares, and regular hexagons. Each of these polygons can be easily analyzed and their perimeters calculated using the steps outlined above.
To summarize:
- Identify the number of sides \( n \).
- Measure the length of one side \( s \).
- Apply the formula \( P = n \times s \).
Understanding and applying this method will help you quickly determine the perimeter of any regular polygon, making it a valuable tool in geometry.
Examples of Regular Polygon Perimeter Calculation
Calculating the perimeter of regular polygons is straightforward due to their equal side lengths. Below are detailed examples demonstrating how to calculate the perimeter of various regular polygons using the perimeter formula \( P = n \times s \), where \( n \) is the number of sides and \( s \) is the length of one side.
Example 1: Equilateral Triangle
An equilateral triangle has three sides of equal length.
- Number of sides \( n \) = 3
- Length of one side \( s \) = 4 units
Using the formula:
\[
P = n \times s = 3 \times 4 = 12 \text{ units}
\]
So, the perimeter of the equilateral triangle is 12 units.
Example 2: Square
A square has four sides of equal length.
- Number of sides \( n \) = 4
- Length of one side \( s \) = 5 units
Using the formula:
\[
P = n \times s = 4 \times 5 = 20 \text{ units}
\]
So, the perimeter of the square is 20 units.
Example 3: Regular Pentagon
A regular pentagon has five sides of equal length.
- Number of sides \( n \) = 5
- Length of one side \( s \) = 3 units
Using the formula:
\[
P = n \times s = 5 \times 3 = 15 \text{ units}
\]
So, the perimeter of the regular pentagon is 15 units.
Example 4: Regular Hexagon
A regular hexagon has six sides of equal length.
- Number of sides \( n \) = 6
- Length of one side \( s \) = 7 units
Using the formula:
\[
P = n \times s = 6 \times 7 = 42 \text{ units}
\]
So, the perimeter of the regular hexagon is 42 units.
Example 5: Regular Octagon
A regular octagon has eight sides of equal length.
- Number of sides \( n \) = 8
- Length of one side \( s \) = 2 units
Using the formula:
\[
P = n \times s = 8 \times 2 = 16 \text{ units}
\]
So, the perimeter of the regular octagon is 16 units.
These examples illustrate how to apply the perimeter formula for various regular polygons. By identifying the number of sides and the length of one side, you can easily calculate the perimeter of any regular polygon.
Calculating the Perimeter of Irregular Polygons
Calculating the perimeter of irregular polygons involves summing the lengths of all its sides. Unlike regular polygons, irregular polygons have sides of different lengths, which requires a more detailed approach. Follow these steps to calculate the perimeter of an irregular polygon:
Steps to Calculate the Perimeter:
- Identify and measure each side: Measure the length of each side of the polygon. This may involve using a ruler or other measuring tools if the polygon is drawn on paper, or using given lengths if they are provided.
- List all side lengths: Write down the length of each side. For an irregular polygon with \( n \) sides, you will have \( s_1, s_2, s_3, \ldots, s_n \).
- Sum the lengths of all sides: Add up the lengths of all the sides to find the perimeter \( P \). The formula is: \[ P = s_1 + s_2 + s_3 + \ldots + s_n \] where \( s_1, s_2, s_3, \ldots, s_n \) are the lengths of the sides.
Example Calculation:
Consider an irregular pentagon with the following side lengths:
- Side 1 (\( s_1 \)) = 3 units
- Side 2 (\( s_2 \)) = 4 units
- Side 3 (\( s_3 \)) = 5 units
- Side 4 (\( s_4 \)) = 6 units
- Side 5 (\( s_5 \)) = 7 units
To find the perimeter, sum all the side lengths:
\[
P = s_1 + s_2 + s_3 + s_4 + s_5 = 3 + 4 + 5 + 6 + 7 = 25 \text{ units}
\]
So, the perimeter of the irregular pentagon is 25 units.
Another example:
Consider an irregular hexagon with the following side lengths:
- Side 1 (\( s_1 \)) = 2.5 units
- Side 2 (\( s_2 \)) = 3.2 units
- Side 3 (\( s_3 \)) = 4.1 units
- Side 4 (\( s_4 \)) = 5.0 units
- Side 5 (\( s_5 \)) = 3.8 units
- Side 6 (\( s_6 \)) = 4.4 units
To find the perimeter, sum all the side lengths:
\[
P = s_1 + s_2 + s_3 + s_4 + s_5 + s_6 = 2.5 + 3.2 + 4.1 + 5.0 + 3.8 + 4.4 = 23 \text{ units}
\]
So, the perimeter of the irregular hexagon is 23 units.
By following these steps, you can calculate the perimeter of any irregular polygon. This process involves careful measurement and addition, ensuring all side lengths are accurately accounted for.
Methods for Irregular Polygon Perimeter Calculation
Calculating the perimeter of irregular polygons, where sides and angles can vary, requires a different approach compared to regular polygons. Here are the methods commonly used:
1. Sum of Side Lengths
For polygons where the side lengths are known, the perimeter is simply the sum of these lengths:
\[ \text{Perimeter} = \sum_{i=1}^{n} \text{Side}_i \]
Steps:
- Identify all side lengths of the polygon.
- Sum these lengths.
- The result is the perimeter of the polygon.
Example:
For a polygon with sides 3 cm, 4 cm, 5 cm, and 6 cm:
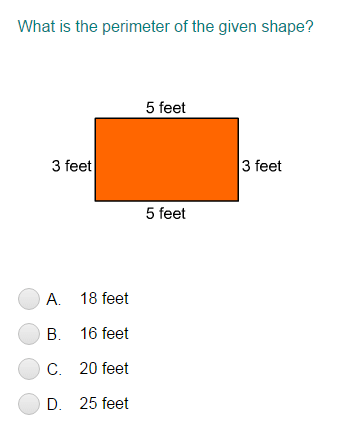
\[ \text{Perimeter} = 3 + 4 + 5 + 6 = 18 \, \text{cm} \]
2. Using Coordinates (Distance Formula)
If the vertices of the polygon are given in a coordinate plane, the perimeter can be calculated using the distance formula between each pair of consecutive vertices:
\[ \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Steps:
- List the coordinates of each vertex.
- Calculate the distance between each pair of consecutive vertices.
- Sum all these distances to get the perimeter.
Example:
For a triangle with vertices at (1,1), (4,1), and (4,5):
- Distance between (1,1) and (4,1): \[ \sqrt{(4-1)^2 + (1-1)^2} = 3 \]
- Distance between (4,1) and (4,5): \[ \sqrt{(4-4)^2 + (5-1)^2} = 4 \]
- Distance between (4,5) and (1,1): \[ \sqrt{(1-4)^2 + (1-5)^2} = 5 \]
- Total Perimeter: \[ 3 + 4 + 5 = 12 \]
3. Dividing into Triangles
If direct measurement or coordinates are not available, sometimes the polygon can be divided into simpler shapes, like triangles, to calculate the perimeter:
Steps:
- Divide the polygon into triangles.
- Calculate the perimeter of each triangle.
- Sum the perimeters of all triangles, ensuring shared sides are not double-counted.
Example:
For a quadrilateral divided into two triangles, if the triangles have perimeters of 8 cm and 10 cm and share a side of 3 cm:
\[ \text{Total Perimeter} = 8 + 10 - 3 = 15 \, \text{cm} \]
4. Measurement Tools
For practical applications, especially with irregular shapes, measurement tools like rulers, tape measures, or digital devices can be used:
Steps:
- Place the tool along each side of the polygon.
- Record the length of each side.
- Sum these lengths to determine the perimeter.
5. Software and Apps
Digital tools and applications can calculate the perimeter of irregular polygons given vertex coordinates or image data:
Steps:
- Input the coordinates or upload an image of the polygon.
- The software computes the perimeter automatically using algorithms.
Popular tools include GIS software and various geometry apps available online.
Examples of Irregular Polygon Perimeter Calculation
Calculating the perimeter of an irregular polygon involves summing the lengths of its sides. Here are detailed examples to illustrate different methods:
Example 1: Known Side Lengths
Consider an irregular quadrilateral with side lengths: 7 cm, 5 cm, 9 cm, and 6 cm.
Steps:
- Identify the lengths of all sides.
- Sum the side lengths:
\[ \text{Perimeter} = 7 + 5 + 9 + 6 \]
- Calculate the total:
\[ \text{Perimeter} = 27 \, \text{cm} \]
Example 2: Using Coordinates
For a pentagon with vertices at (2,3), (5,7), (6,4), (4,2), and (1,2):
Steps:
- List the coordinates of each vertex.
- Calculate the distance between each pair of consecutive vertices using the distance formula:
- Distance between (2,3) and (5,7):
\[ \sqrt{(5-2)^2 + (7-3)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
- Distance between (5,7) and (6,4):
\[ \sqrt{(6-5)^2 + (4-7)^2} = \sqrt{1 + 9} = \sqrt{10} \approx 3.16 \]
- Distance between (6,4) and (4,2):
\[ \sqrt{(4-6)^2 + (2-4)^2} = \sqrt{4 + 4} = \sqrt{8} \approx 2.83 \]
- Distance between (4,2) and (1,2):
\[ \sqrt{(1-4)^2 + (2-2)^2} = \sqrt{9 + 0} = \sqrt{9} = 3 \]
- Distance between (1,2) and (2,3):
\[ \sqrt{(2-1)^2 + (3-2)^2} = \sqrt{1 + 1} = \sqrt{2} \approx 1.41 \]
- Sum these distances:
\[ \text{Perimeter} \approx 5 + 3.16 + 2.83 + 3 + 1.41 = 15.4 \, \text{units} \]
Example 3: Measurement from a Diagram
Consider an irregular hexagon where you measure the sides directly from a diagram:
Measured side lengths are: 4.2 cm, 3.8 cm, 5.1 cm, 4.0 cm, 6.3 cm, and 2.5 cm.
Steps:
- Measure each side of the hexagon using a ruler or a measuring tool.
- Sum the measured lengths:
\[ \text{Perimeter} = 4.2 + 3.8 + 5.1 + 4.0 + 6.3 + 2.5 \]
- Calculate the total:
\[ \text{Perimeter} = 25.9 \, \text{cm} \]
Example 4: Software Calculation
Using a geometry software, input the vertices of a decagon as: (0,0), (2,3), (4,6), (6,8), (7,7), (8,5), (7,3), (5,2), (3,1), (1,0).
Steps:
- Enter the coordinates into the software.
- Allow the software to compute the distances between consecutive vertices and sum them:
- The software provides the total perimeter:
For illustration, assume the calculated distances are:
\[ \text{Distances} = 3.61, 3.61, 2.83, 1.41, 2.24, 2.24, 3.16, 2.24, 2.24, 1 \]
\[ \text{Perimeter} \approx 24.58 \, \text{units} \]
Practical Applications of Perimeter Calculation
Perimeter calculation has numerous practical applications across various fields. Here are some key examples:
1. Construction and Architecture
Perimeter calculation is crucial in construction and architecture for determining the boundary lengths of various structures and plots:
- Plot Layout: Helps in planning the layout of a plot by knowing the boundary lengths to allocate space for buildings, gardens, etc.
- Fencing: Determines the amount of fencing material needed to enclose a property.
- Flooring: Calculates the perimeter for installing baseboards or molding around a room.
2. Landscaping and Gardening
Used in designing garden beds, pathways, and enclosing areas:
- Garden Borders: Helps in laying out garden borders or edging.
- Pathways: Determines the perimeter of garden paths for material estimation.
- Water Features: Assists in the design of ponds and water features by calculating liner and edging material.
3. Manufacturing and Material Cutting
Important in industrial design and manufacturing processes where precise material measurements are necessary:
- Fabric Cutting: Calculates the perimeter of fabric pieces for efficient cutting and minimizing waste.
- Metal Sheets: Determines the perimeter for cutting metal sheets in automotive and appliance manufacturing.
- Packaging: Helps in designing packaging materials, including calculating the perimeter of labels and wraps.
4. Surveying and Land Measurement
In surveying, perimeter calculation helps in mapping and defining property boundaries:
- Land Division: Used in dividing large plots into smaller sections by measuring boundary lines.
- Property Valuation: Helps in the valuation of property by accurately defining its boundaries.
- Legal Documentation: Essential for creating legal property descriptions and deeds.
5. Textile and Fashion Design
Used in designing clothing patterns and textile layouts:
- Pattern Making: Calculates the perimeter of clothing patterns for fitting and seam allowances.
- Textile Layouts: Determines the perimeter of fabric layouts to optimize material usage.
- Accessory Design: Helps in designing accessories like belts and trims by knowing the perimeter for fitting purposes.
6. Urban Planning
In urban planning, perimeter calculation assists in designing and managing city layouts:
- Parks and Recreation: Helps in the layout of parks by determining the perimeter of various sections and facilities.
- Public Works: Used in planning the perimeter of roads, sidewalks, and public buildings.
- Zoning: Assists in zoning regulations by defining the boundaries of different zones accurately.
7. Art and Design
Artists and designers use perimeter calculation for various creative purposes:
- Sculpture and Installation: Calculates the perimeter of sculptures and installations for base planning and material estimation.
- Framing: Determines the perimeter of artwork for framing purposes.
- Graphic Design: Used in creating layouts and templates for design projects.
8. Agriculture
Farmers and agricultural planners use perimeter calculations for managing land and resources:
- Field Planning: Helps in planning fields and crop layouts by determining the perimeter for irrigation and fencing.
- Resource Allocation: Used in allocating resources like water and fertilizer based on field perimeters.
- Livestock Management: Calculates the perimeter of enclosures and pastures for livestock management.
Common Mistakes and Tips
When calculating the perimeter of polygons, several common mistakes can arise. Here are key points to watch for and tips to ensure accurate calculations:
1. Mistake: Incorrect Side Lengths
Failing to measure or use the correct side lengths is a frequent error.
Tip: Always double-check measurements or given values before performing calculations. If using coordinates, verify each point is plotted correctly.
- For diagrams, use precise tools like rulers or calipers for accurate measurements.
- In coordinate geometry, cross-check the coordinates with the diagram.
2. Mistake: Omitting Sides
Another common mistake is forgetting to include all sides in the calculation.
Tip: Ensure all sides are accounted for by systematically working around the polygon.
- Label each side or vertex in a sequence to avoid missing any.
- Create a checklist of sides and tick them off as you calculate their lengths.
3. Mistake: Double-Counting Shared Sides
When dividing polygons into simpler shapes, shared sides can be accidentally counted more than once.
Tip: Be mindful of shared sides in internal divisions and subtract them if necessary.
- Highlight or note down shared sides to ensure they are counted only once.
- Re-calculate the shared length and adjust the total accordingly.
4. Mistake: Misapplying the Distance Formula
Errors in applying the distance formula can lead to incorrect side lengths.
Tip: Use the correct formula and ensure each step in the calculation is accurate:
\[ \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Double-check the coordinate pairs before substituting them into the formula.
- Verify calculations by repeating them or using a calculator.
5. Mistake: Incorrect Unit Handling
Mixing different units or failing to convert units can result in wrong perimeters.
Tip: Always use consistent units throughout your calculations.
- If side lengths are given in different units, convert them to a common unit before summing.
- Check the final perimeter to ensure the unit is correctly stated (e.g., cm, meters).
6. Mistake: Rounding Errors
Rounding too early in the calculation process can introduce errors.
Tip: Maintain as much precision as possible until the final result.
- Carry intermediate results to a few more decimal places than needed.
- Round only the final result to the required precision.
7. Mistake: Misidentifying Polygon Types
Misidentifying the type of polygon (regular vs. irregular) can lead to incorrect methods being used.
Tip: Confirm the polygon type before choosing a calculation method.
- For regular polygons, verify that all sides and angles are equal.
- For irregular polygons, ensure each side is measured or calculated individually.
8. Mistake: Overlooking Internal Angles
Sometimes, internal angles can affect the perimeter when working with certain methods.
Tip: Be aware of internal angles and their impact, especially in complex shapes.
- Consider using trigonometric methods if internal angles are known.
- For complex shapes, verify angles using geometric principles or software tools.
General Tips
- Use Reliable Tools: Utilize reliable measuring tools and software for accurate results.
- Practice Problem-Solving: Regularly practice solving perimeter problems to become familiar with different scenarios.
- Seek Verification: Cross-check your results with peers or online calculators for confirmation.
- Document Each Step: Keep a clear record of each calculation step to track and correct errors easily.
Advanced Topics in Perimeter Calculation
In this section, we will delve into more complex aspects of calculating the perimeter of polygons. This includes dealing with polygons on a coordinate plane, the use of various advanced mathematical techniques, and leveraging technology for precise calculations.
Polygons on a Coordinate Plane
When working with polygons on a coordinate plane, we can calculate the perimeter by determining the distance between consecutive vertices. This is particularly useful for irregular polygons where side lengths are not directly given.
Consider a polygon with vertices at \( (x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n) \). The distance between two points \( (x_i, y_i) \) and \( (x_{i+1}, y_{i+1}) \) is given by the distance formula:
\[
d = \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2}
\]
To find the perimeter \( P \), sum the distances between consecutive vertices:
\[
P = \sum_{i=1}^{n-1} \sqrt{(x_{i+1} - x_i)^2 + (y_{i+1} - y_i)^2} + \sqrt{(x_1 - x_n)^2 + (y_1 - y_n)^2}
\]
Using Technology for Perimeter Calculation
Various software tools and online calculators can significantly simplify the process of perimeter calculation. These tools often allow you to input the coordinates of vertices or side lengths, and they handle the computation, reducing human error.
- Geometric Drawing Tools: Programs like GeoGebra and Desmos can be used to plot polygons and automatically calculate their perimeters.
- Programming: Writing scripts in languages such as Python can automate the perimeter calculation for complex polygons.
For example, a simple Python script using the math library might look like this:
import math
def distance(x1, y1, x2, y2):
return math.sqrt((x2 - x1)**2 + (y2 - y1)**2)
def perimeter(vertices):
n = len(vertices)
perim = 0
for i in range(n):
x1, y1 = vertices[i]
x2, y2 = vertices[(i+1) % n]
perim += distance(x1, y1, x2, y2)
return perim
vertices = [(1, 2), (4, 6), (7, 2)]
print("Perimeter:", perimeter(vertices))
Perimeter Calculation for Complex Polygons
For complex polygons, especially those that are self-intersecting or have a large number of sides, advanced computational geometry techniques are required. This might involve:
- Decomposition: Breaking the polygon into simpler shapes (triangles, rectangles) whose perimeters are easier to calculate.
- Integration Methods: Using calculus-based methods to integrate over the edges of the polygon.
Real-World Applications
Advanced perimeter calculations are crucial in various fields such as computer graphics, geographical information systems (GIS), and architectural design. Accurate perimeter measurements can impact material estimates, structural integrity assessments, and even urban planning.
Summary
Understanding and calculating the perimeter of polygons, especially in advanced contexts, requires a blend of mathematical techniques and technological tools. Mastering these skills can provide significant advantages in both academic and professional settings.

Perimeter in Coordinate Geometry
In coordinate geometry, calculating the perimeter of a polygon involves determining the distance between consecutive vertices. This method is particularly useful for irregular polygons where side lengths are not directly provided. The formula for the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is derived from the Pythagorean theorem:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
To calculate the perimeter of a polygon with vertices \((x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\), follow these steps:
- Identify the coordinates of each vertex of the polygon.
- Apply the distance formula to find the length of each side.
- Sum the lengths of all sides to obtain the perimeter.
Consider a polygon with vertices \((x_1, y_1), (x_2, y_2), (x_3, y_3)\) and \((x_4, y_4)\). The perimeter \(P\) can be calculated as follows:
- Calculate the distance between \((x_1, y_1)\) and \((x_2, y_2)\): \[ d_1 = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
- Calculate the distance between \((x_2, y_2)\) and \((x_3, y_3)\): \[ d_2 = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \]
- Calculate the distance between \((x_3, y_3)\) and \((x_4, y_4)\): \[ d_3 = \sqrt{(x_4 - x_3)^2 + (y_4 - y_3)^2} \]
- Calculate the distance between \((x_4, y_4)\) and \((x_1, y_1)\): \[ d_4 = \sqrt{(x_1 - x_4)^2 + (y_1 - y_4)^2} \]
The perimeter \(P\) of the polygon is then the sum of these distances:
\[ P = d_1 + d_2 + d_3 + d_4 \]
Let's illustrate this with an example. Suppose we have a polygon with vertices at \((2, 3)\), \((5, 11)\), \((12, 8)\), and \((9, 5)\). We can calculate the distances between these points as follows:
| Between \((2, 3)\) and \((5, 11)\): | \[ d_1 = \sqrt{(5 - 2)^2 + (11 - 3)^2} = \sqrt{3^2 + 8^2} = \sqrt{9 + 64} = \sqrt{73} \approx 8.54 \] |
| Between \((5, 11)\) and \((12, 8)\): | \[ d_2 = \sqrt{(12 - 5)^2 + (8 - 11)^2} = \sqrt{7^2 + (-3)^2} = \sqrt{49 + 9} = \sqrt{58} \approx 7.62 \] |
| Between \((12, 8)\) and \((9, 5)\): | \[ d_3 = \sqrt{(9 - 12)^2 + (5 - 8)^2} = \sqrt{(-3)^2 + (-3)^2} = \sqrt{9 + 9} = \sqrt{18} \approx 4.24 \] |
| Between \((9, 5)\) and \((2, 3)\): | \[ d_4 = \sqrt{(2 - 9)^2 + (3 - 5)^2} = \sqrt{(-7)^2 + (-2)^2} = \sqrt{49 + 4} = \sqrt{53} \approx 7.28 \] |
Finally, the perimeter \(P\) is:
\[ P = 8.54 + 7.62 + 4.24 + 7.28 = 27.68 \]
Using these steps, you can calculate the perimeter of any polygon given its vertices in a coordinate plane. This method is efficient and widely applicable, particularly in advanced geometry problems.
Using Technology for Perimeter Calculation
In the modern era, technology offers numerous tools and software that simplify the process of calculating the perimeter of polygons, whether regular or irregular. Below are some of the common technologies and methods used:
- Geometry Software: Programs such as GeoGebra and Desmos provide interactive environments where you can draw polygons and automatically calculate their perimeter.
- Online Calculators: Various websites offer polygon perimeter calculators. These tools typically require you to input the lengths of the sides, and they compute the perimeter for you.
- Coordinate Geometry Tools: For polygons defined by vertices on a coordinate plane, software like MATLAB or Python libraries such as NumPy can be used to calculate distances between points and sum them to find the perimeter. Here’s a step-by-step guide using Python:
- List the coordinates of the vertices.
- Use the distance formula to calculate the length of each side:
\[
\text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\] - Sum the lengths of all sides to get the perimeter.
Example Python Code:
import numpy as np
# Define the coordinates of the vertices
vertices = np.array([[0, 0], [0, 4], [4, 4], [4, 0]])
# Calculate the distances between consecutive vertices
distances = np.sqrt(np.sum(np.diff(vertices, axis=0)**2, axis=1))
# Add the distance between the last and first vertex to close the polygon
distances = np.append(distances, np.sqrt(np.sum((vertices[0] - vertices[-1])**2)))
# Calculate the perimeter
perimeter = np.sum(distances)
print("Perimeter:", perimeter)
- CAD Software: Computer-Aided Design (CAD) programs like AutoCAD allow precise drawing and measurement of polygonal shapes, making it easy to calculate perimeters for complex designs.
- Graphing Calculators: Advanced graphing calculators, such as the TI-84, have built-in functions to calculate distances and can be used for perimeter calculations in coordinate geometry.
These technologies enhance accuracy and efficiency in perimeter calculations, making them accessible and straightforward, even for complex polygons.
Conclusion and Summary
Understanding the perimeter of a polygon, whether regular or irregular, is fundamental in geometry and has various practical applications. Here is a summary of the key points covered:
- Definition: The perimeter of a polygon is the total length of its sides.
- Regular Polygons: For regular polygons, where all sides and angles are equal, the perimeter can be calculated using the formula:
\[ P = n \times s \]
where \( n \) is the number of sides and \( s \) is the length of one side. - Irregular Polygons: For irregular polygons, where sides may not be equal, the perimeter is found by summing the lengths of all sides:
\[ P = s_1 + s_2 + s_3 + \ldots + s_n \]
- Using Technology: Various tools and software, such as GeoGebra, Desmos, and MATLAB, can aid in calculating the perimeter by providing visualizations and precise measurements.
- Practical Applications: Calculating perimeters is essential in fields like architecture, engineering, and land surveying, where precise measurements are crucial.
- Common Mistakes: Ensure all sides are measured correctly and consistently, especially for irregular polygons. Double-check calculations to avoid errors.
- Advanced Topics: In coordinate geometry, the distance formula can be used to determine side lengths when vertices are given in a coordinate plane:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
By mastering these concepts and utilizing technological tools, one can efficiently calculate the perimeter of any polygon. This knowledge is not only academically important but also highly applicable in various real-world scenarios.
Additional Resources
To further enhance your understanding and calculation of polygon perimeters, here are some valuable resources:
- Math Open Reference:
- - A comprehensive guide to calculating the perimeter of various types of polygons, including interactive examples to visualize the calculations.
- Topics include:
- General polygon definitions
- Perimeter formulas for regular and irregular polygons
- Applications and examples
- Story of Mathematics:
- - Detailed explanations and examples for finding the perimeter of different polygon types, from triangles to trapezoids.
- Examples provided include step-by-step solutions for:
- Triangles
- Squares and rhombuses
- Rectangles and parallelograms
- Trapezoids
- Tutors.com:
- - Offers a mix of video tutorials, written explanations, and practical examples to solidify your understanding.
- Key sections include:
- General perimeter calculation methods
- Formulas for regular and irregular polygons
- Real-world application problems
These resources will provide you with the tools and knowledge to confidently calculate the perimeter of any polygon you encounter, whether in academic settings or practical applications.
Frequently Asked Questions
-
Q: What is the perimeter of a polygon?
A: The perimeter of a polygon is the total distance around the outside of the polygon. It is calculated by adding together the lengths of all the sides of the polygon.
-
Q: How do you find the perimeter of a regular polygon?
A: For a regular polygon, where all sides are of equal length, the perimeter (P) can be found using the formula:
\[ P = n \times s \]
where n is the number of sides, and s is the length of one side. For example, the perimeter of a regular hexagon (6 sides) with each side measuring 4 meters would be:
\[ P = 6 \times 4 = 24 \text{ meters} \]
-
Q: How do you calculate the perimeter of an irregular polygon?
A: For an irregular polygon, you simply add the lengths of all the sides. For instance, if an irregular polygon has sides of lengths 3 cm, 4 cm, 5 cm, and 6 cm, the perimeter is:
\[ P = 3 + 4 + 5 + 6 = 18 \text{ cm} \]
-
Q: What if the lengths of some sides of the polygon are unknown?
A: If the lengths of some sides are unknown, you will need to find those lengths before calculating the perimeter. In some cases, properties of the polygon (like the fact that opposite sides of a rectangle are equal) can help determine these lengths.
-
Q: How can I find the perimeter of a polygon on a coordinate plane?
A: To find the perimeter of a polygon on a coordinate plane, use the distance formula to find the lengths of each side. For two points \((x_1, y_1)\) and \((x_2, y_2)\), the distance \(d\) is calculated as:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Sum the lengths of all sides to get the perimeter.
-
Q: Are there tools available to help calculate the perimeter of complex polygons?
A: Yes, various geometry software and online calculators can assist in calculating the perimeter of complex polygons. These tools often allow you to input the coordinates of the vertices or the lengths of the sides and automatically compute the perimeter.
Chu vi của một đa giác
Chu vi của một Đa giác
READ MORE:
Chu vi của một đa giác là gì?
Chu vi của một đa giác