Topic area and perimeter worded problems: Explore the intricacies of area and perimeter through engaging worded problems in this comprehensive guide. From basic concepts to advanced strategies, this article equips you with the skills to tackle any mathematical challenge. Dive into practice exercises with solutions and unlock your potential in problem-solving.
Table of Content
- Area and Perimeter Worded Problems
- 1. Introduction to Area and Perimeter
- 2. Understanding Worded Problems
- 3. Basic Concepts of Area and Perimeter
- 4. Worded Problems Involving Rectangles
- 5. Worded Problems Involving Squares
- 6. Worded Problems Involving Circles
- 7. Worded Problems Involving Triangles
- 8. Advanced Worded Problems
- 9. Strategies and Tips for Solving Worded Problems
- 10. Practice Exercises with Solutions
- YOUTUBE: Video này hướng dẫn cách giải bài toán về diện tích và chu vi, cụ thể là tính chiều rộng của chuồng chó. Phù hợp cho học sinh và người học muốn cải thiện kỹ năng toán học của mình.
Area and Perimeter Worded Problems
Understanding the concepts of area and perimeter through worded problems is essential for students to apply mathematical principles to real-world situations. Here is a detailed synthesis of information and examples to help grasp these concepts effectively.
Rectangular Area and Perimeter Word Problems
Rectangles are common shapes used to illustrate area and perimeter problems. The formulas are straightforward:
- Area: \( \text{Area} = \text{length} \times \text{width} \)
- Perimeter: \( \text{Perimeter} = 2(\text{length} + \text{width}) \)
For example, a rectangular garden measuring 10 meters by 12 meters has:
- Area: \( 10 \, \text{m} \times 12 \, \text{m} = 120 \, \text{m}^2 \)
- Perimeter: \( 2(10 \, \text{m} + 12 \, \text{m}) = 44 \, \text{m} \)
Triangular Area and Perimeter Word Problems
Triangles are another common shape. The area and perimeter calculations involve:
- Area: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
- Perimeter: Sum of all three sides
Real-Life Applications
Word problems often relate to real-life scenarios, such as finding the amount of material needed for construction or the distance around a park. For example, to cover a rectangular floor with tiles:
- Calculate the area of the floor
- Divide by the area of one tile
Given a floor of 10 feet by 12 feet and tiles of 1 square foot each:
- Number of tiles needed: \( \frac{120 \, \text{sq ft}}{1 \, \text{sq ft per tile}} = 120 \text{ tiles} \)
Complex Shapes
Sometimes, the shapes are more complex, requiring the division into simpler shapes. For example, an irregular garden can be divided into rectangles to find the total perimeter.
Interactive Practice
To reinforce learning, interactive worksheets and online practice problems are beneficial. These resources often provide step-by-step solutions and practice problems to help students visualize and solve area and perimeter problems.
| Resource | Description |
| Khan Academy | Offers practice problems and instructional videos on area and perimeter of rectangles. |
| Live Worksheets | Interactive worksheets for practicing area and perimeter word problems. |

READ MORE:
1. Introduction to Area and Perimeter
Understanding the concepts of area and perimeter is fundamental in geometry and essential for solving various mathematical problems. These concepts not only apply to academic exercises but also have practical applications in everyday life, such as in construction, design, and space planning.
The perimeter of a shape is the total length of its boundaries. It is measured in linear units, such as meters or feet. For instance, the perimeter of a rectangle is the sum of all its sides, calculated as:
\[
\text{Perimeter of a rectangle} = 2 \times (\text{length} + \text{width})
\]
On the other hand, the area of a shape is the measure of the space it occupies. It is measured in square units, such as square meters or square feet. For a rectangle, the area is determined by multiplying its length by its width:
\[
\text{Area of a rectangle} = \text{length} \times \text{width}
\]
These formulas are the foundation for solving more complex worded problems involving different geometric shapes. To further illustrate these concepts, let's look at the definitions and formulas for the area and perimeter of some common shapes:
- Square
- Perimeter: \[ \text{Perimeter of a square} = 4 \times \text{side} \]
- Area: \[ \text{Area of a square} = \text{side}^2 \]
- Circle
- Perimeter (Circumference): \[ \text{Circumference of a circle} = 2 \pi \times \text{radius} \]
- Area: \[ \text{Area of a circle} = \pi \times \text{radius}^2 \]
- Triangle
- Perimeter: The sum of all three sides.
- Area: \[ \text{Area of a triangle} = \frac{1}{2} \times \text{base} \times \text{height} \]
By mastering these basic formulas, you will be well-equipped to tackle a wide variety of area and perimeter problems. As we proceed, we will explore various worded problems that will help deepen your understanding and application of these concepts.
2. Understanding Worded Problems
Worded problems, also known as word problems, are mathematical problems presented in a narrative format. These problems require you to read and comprehend the text, identify the relevant mathematical concepts, and then apply the appropriate formulas and strategies to find the solution.
Here are the steps to effectively understand and solve worded problems involving area and perimeter:
- Read the Problem Carefully: Begin by reading the entire problem thoroughly. Pay attention to details and make sure you understand what is being asked.
- Identify Key Information: Look for important numbers, units of measurement, and keywords that indicate specific mathematical operations (e.g., total, difference, perimeter, area).
- Draw a Diagram: Visualize the problem by sketching a diagram. This can help in understanding the shape and the relationship between different parts of the problem.
- Write Down the Formulas: Recall and write down the relevant formulas for area and perimeter. For example:
- Perimeter of a rectangle: \( P = 2(l + w) \)
- Area of a rectangle: \( A = l \times w \)
- Perimeter of a circle: \( P = 2\pi r \)
- Area of a circle: \( A = \pi r^2 \)
- Perimeter of a triangle: \( P = a + b + c \)
- Area of a triangle: \( A = \frac{1}{2} \times \text{base} \times \text{height} \)
- Set Up Equations: Using the information from the problem and the formulas, set up the equations needed to solve for the unknown values.
- Solve the Equations: Solve the equations step by step, ensuring each calculation is correct. Be mindful of units and convert them if necessary.
- Check Your Work: After finding the solution, review each step to ensure no mistakes were made. Verify that the solution makes sense in the context of the problem.
Let's look at a sample problem to illustrate these steps:
Example: Emily has a square mirror with sides of 60 cm. What is the perimeter and area of Emily's mirror?
- Read the problem carefully: Emily's mirror is square with sides of 60 cm.
- Identify key information: Side length = 60 cm.
- Draw a diagram: Sketch a square and label the sides as 60 cm.
- Write down the formulas:
- Perimeter of a square: \( P = 4s \)
- Area of a square: \( A = s^2 \)
- Set up equations:
- Perimeter: \( P = 4 \times 60 \)
- Area: \( A = 60^2 \)
- Solve the equations:
- Perimeter: \( P = 240 \) cm
- Area: \( A = 3600 \) cm2
- Check your work: Verify that the calculations are correct and the units are appropriate.
By following these steps, you can systematically approach and solve worded problems involving area and perimeter, ensuring accuracy and comprehension.
3. Basic Concepts of Area and Perimeter
Understanding the basic concepts of area and perimeter is fundamental to solving worded problems in geometry. These concepts help us determine the size and boundary length of various shapes. Let's explore these concepts step by step.
Area
The area of a shape is the measure of the space it occupies. It is typically measured in square units (e.g., square meters, square feet).
- Rectangle: The area of a rectangle is calculated by multiplying its length (l) by its width (w): \[ \text{Area} = l \times w \]
- Square: Since all sides of a square are equal, the area is the side length (s) squared: \[ \text{Area} = s^2 \]
- Circle: The area of a circle is calculated using the radius (r) and the constant π (pi): \[ \text{Area} = \pi r^2 \]
- Triangle: The area of a triangle is found using its base (b) and height (h): \[ \text{Area} = \frac{1}{2} b h \]
Perimeter
The perimeter of a shape is the total length of its boundary. It is the sum of the lengths of all sides of the shape.
- Rectangle: The perimeter of a rectangle is calculated by adding twice the length and twice the width: \[ \text{Perimeter} = 2l + 2w \]
- Square: The perimeter of a square is four times the side length: \[ \text{Perimeter} = 4s \]
- Circle: The perimeter (circumference) of a circle is found using the radius and the constant π: \[ \text{Perimeter} = 2\pi r \]
- Triangle: The perimeter of a triangle is the sum of the lengths of its three sides: \[ \text{Perimeter} = a + b + c \]
Units of Measurement
It is important to ensure that all measurements are in the same unit when calculating area and perimeter. Common units include:
- Length: meters (m), centimeters (cm), feet (ft), inches (in)
- Area: square meters (m2), square centimeters (cm2), square feet (ft2), square inches (in2)
Applications
Knowing how to calculate area and perimeter is essential for various real-life applications, such as:
- Determining the amount of material needed for a project (e.g., flooring, painting)
- Planning the layout of gardens, rooms, or other spaces
- Solving problems related to fencing or border placement
4. Worded Problems Involving Rectangles
Word problems involving rectangles often require finding the area or perimeter of a rectangle given certain dimensions or solving for missing dimensions based on given information. Here, we will go through some common types of problems and strategies to solve them.
4.1. Area of a Rectangle
The area of a rectangle can be found using the formula:
\[ \text{Area} = \text{length} \times \text{width} \]
Example Problem:
- A rectangular garden has a length of 10 meters and a width of 5 meters. What is the area of the garden?
Solution:
\[ \text{Area} = 10 \, \text{m} \times 5 \, \text{m} = 50 \, \text{m}^2 \]
4.2. Perimeter of a Rectangle
The perimeter of a rectangle can be found using the formula:
\[ \text{Perimeter} = 2 \times (\text{length} + \text{width}) \]
Example Problem:
- A rectangular field has a length of 12 meters and a width of 7 meters. What is the perimeter of the field?
Solution:
\[ \text{Perimeter} = 2 \times (12 \, \text{m} + 7 \, \text{m}) = 2 \times 19 \, \text{m} = 38 \, \text{m} \]
4.3. Finding Missing Dimensions
Sometimes, you may need to find a missing dimension of a rectangle given its area or perimeter.
Example Problem:
- The perimeter of a rectangle is 24 meters, and its length is 7 meters. What is its width?
Solution:
\[ \text{Perimeter} = 2 \times (\text{length} + \text{width}) \]
\[ 24 = 2 \times (7 + \text{width}) \]
\[ 24 = 14 + 2 \times \text{width} \]
\[ 10 = 2 \times \text{width} \]
\[ \text{width} = 5 \, \text{m} \]
4.4. Practical Application Problems
These problems often involve real-life scenarios where you apply the formulas for area and perimeter.
Example Problem:
- A rectangular garden needs a fence around it. The garden is 15 meters long and 8 meters wide. How much fencing material is needed?
Solution:
\[ \text{Perimeter} = 2 \times (15 \, \text{m} + 8 \, \text{m}) = 2 \times 23 \, \text{m} = 46 \, \text{m} \]
4.5. Optimizing Dimensions
Sometimes, you might need to optimize the dimensions of a rectangle to maximize or minimize the area or perimeter.
Example Problem:
- You have 40 meters of fencing to create a rectangular garden. What dimensions will give you the maximum area?
Solution:
To maximize the area, the garden should be as close to a square as possible. For a perimeter of 40 meters:
\[ 2 \times (\text{length} + \text{width}) = 40 \]
\[ \text{length} + \text{width} = 20 \]
Let’s consider equal lengths and widths (a square):
\[ \text{length} = \text{width} = 10 \, \text{m} \]
Thus, the maximum area is:
\[ \text{Area} = 10 \, \text{m} \times 10 \, \text{m} = 100 \, \text{m}^2 \]
These are just a few examples of the types of worded problems involving rectangles. Practicing various problems will help you understand the concepts and improve your problem-solving skills.

5. Worded Problems Involving Squares
Understanding worded problems involving squares is crucial for solving various mathematical and real-life problems. This section provides detailed explanations and step-by-step solutions for common types of problems involving squares.
1. Calculating the Area and Perimeter of a Square
- Area: The area of a square is calculated using the formula \( A = a^2 \), where \( a \) is the length of one side of the square.
- Perimeter: The perimeter of a square is calculated using the formula \( P = 4a \), where \( a \) is the length of one side of the square.
Example 1:
A square garden has a side length of 5 meters. Calculate the area and the perimeter of the garden.
- Area: \( A = 5^2 = 25 \) square meters
- Perimeter: \( P = 4 \times 5 = 20 \) meters
2. Comparing Areas of Squares and Rectangles
When comparing the areas of a square and a rectangle, ensure both shapes have the same area to find relationships between their dimensions.
Example 2:
A square and a rectangle have the same area. The rectangle has a length of 9 cm and a width of 4 cm. Find the side length of the square.
- Area of rectangle: \( 9 \times 4 = 36 \) square cm
- Side length of the square: \( \sqrt{36} = 6 \) cm
3. Doubling the Side Length of a Square
Doubling the side length of a square increases its area by a factor of four.
Example 3:
The side of a square is 3 cm. If its side is doubled, how many times is the area of the new square bigger than the area of the older square?
- Original area: \( 3^2 = 9 \) square cm
- New side length: \( 2 \times 3 = 6 \) cm
- New area: \( 6^2 = 36 \) square cm
- The new area is \( \frac{36}{9} = 4 \) times bigger
4. Finding the Area Using Diagonals
The area of a square can also be calculated using its diagonal.
Example 4:
In a square, if the length of each diagonal is 2 cm, find its area.
- Formula: \( A = \frac{1}{2} \times d^2 \)
- Area: \( A = \frac{1}{2} \times 2^2 = 2 \) square cm
5. Practical Applications
Worded problems often involve real-life applications, such as tiling floors or designing gardens.
Example 5:
How many square tiles with a side length of 3 cm are needed to cover a rectangular floor of 27 cm by 10 cm?
- Area of one tile: \( 3^2 = 9 \) square cm
- Area of the floor: \( 27 \times 10 = 270 \) square cm
- Number of tiles: \( \frac{270}{9} = 30 \) tiles
These examples illustrate the basic concepts and applications of squares in worded problems, enhancing your problem-solving skills and understanding of geometry.
6. Worded Problems Involving Circles
When solving worded problems involving circles, it's essential to understand the basic properties and formulas associated with circles. Here are the key concepts:
- Radius (r): The distance from the center of the circle to any point on its circumference.
- Diameter (d): The distance across the circle, passing through the center. The diameter is twice the radius (d = 2r).
- Circumference (C): The total distance around the circle. The formula for the circumference is \(C = 2\pi r\) or \(C = \pi d\).
- Area (A): The total space enclosed within the circle. The formula for the area is \(A = \pi r^2\).
Let's look at some examples and steps to solve worded problems involving circles.
Example 1: Finding the Circumference
Problem: A circular garden has a radius of 7 meters. Calculate the circumference of the garden.
- Identify the radius (r) from the problem: \( r = 7 \) meters.
- Use the formula for circumference: \( C = 2\pi r \).
- Substitute the value of the radius into the formula: \( C = 2\pi \times 7 \).
- Simplify the expression: \( C = 14\pi \).
- Approximate using \( \pi \approx 3.14 \): \( C \approx 14 \times 3.14 = 43.96 \) meters.
Answer: The circumference of the garden is approximately 43.96 meters.
Example 2: Finding the Area
Problem: A circular table top has a diameter of 1.5 meters. Calculate the area of the table top.
- Identify the diameter (d) from the problem: \( d = 1.5 \) meters.
- Calculate the radius: \( r = \frac{d}{2} = \frac{1.5}{2} = 0.75 \) meters.
- Use the formula for area: \( A = \pi r^2 \).
- Substitute the value of the radius into the formula: \( A = \pi \times (0.75)^2 \).
- Simplify the expression: \( A = \pi \times 0.5625 \).
- Approximate using \( \pi \approx 3.14 \): \( A \approx 3.14 \times 0.5625 = 1.77 \) square meters.
Answer: The area of the table top is approximately 1.77 square meters.
Example 3: Word Problem Involving Both Circumference and Area
Problem: A wheel has a radius of 0.5 meters. Calculate both the circumference and the area of the wheel.
- Identify the radius (r) from the problem: \( r = 0.5 \) meters.
- Finding the Circumference:
- Use the formula for circumference: \( C = 2\pi r \).
- Substitute the value of the radius into the formula: \( C = 2\pi \times 0.5 \).
- Simplify the expression: \( C = \pi \).
- Approximate using \( \pi \approx 3.14 \): \( C \approx 3.14 \) meters.
- Finding the Area:
- Use the formula for area: \( A = \pi r^2 \).
- Substitute the value of the radius into the formula: \( A = \pi \times (0.5)^2 \).
- Simplify the expression: \( A = \pi \times 0.25 \).
- Approximate using \( \pi \approx 3.14 \): \( A \approx 3.14 \times 0.25 = 0.785 \) square meters.
Answer: The circumference of the wheel is approximately 3.14 meters, and the area is approximately 0.785 square meters.
7. Worded Problems Involving Triangles
Triangles are a fundamental shape in geometry, and problems involving their area and perimeter can be approached systematically. Below are several types of worded problems involving triangles, along with strategies for solving them.
Basic Concepts
- Area of a Triangle: The area \( A \) of a triangle is given by the formula \( A = \frac{1}{2} \times \text{base} \times \text{height} \).
- Perimeter of a Triangle: The perimeter \( P \) of a triangle is the sum of the lengths of its sides.
Example Problems
Problem 1: Finding the Area
The height of a triangle is 4 inches more than twice the length of the base. The area of the triangle is 35 square inches. Find the height of the triangle.
- Let the base be \( b \) inches.
- The height \( h \) is \( 2b + 4 \) inches.
- Using the area formula: \( \frac{1}{2} \times b \times (2b + 4) = 35 \).
- Solve for \( b \):
- \( b(2b + 4) = 70 \)
- \( 2b^2 + 4b - 70 = 0 \)
- Using the quadratic formula \( b = \frac{-B \pm \sqrt{B^2 - 4AC}}{2A} \), where \( A = 2 \), \( B = 4 \), and \( C = -70 \).
- \( b = \frac{-4 \pm \sqrt{16 + 560}}{4} = \frac{-4 \pm 24}{4} \)
- The positive solution is \( b = 5 \) inches.
- Thus, the height \( h = 2 \times 5 + 4 = 14 \) inches.
Problem 2: Perimeter of a Triangle
The sides of a triangle are given as \( 3x \), \( x - 1 \), and \( 3x + 1 \). If the perimeter is 56 meters, find the area.
- First, find \( x \) using the perimeter:
- \( 3x + (x - 1) + (3x + 1) = 56 \)
- \( 7x = 56 \)
- \( x = 8 \)
- The sides are \( 24 \)m, \( 7 \)m, and \( 25 \)m.
- To find the area, use Heron's formula:
- Semi-perimeter \( s = \frac{24 + 7 + 25}{2} = 28 \)m
- Area \( A = \sqrt{s(s-a)(s-b)(s-c)} \)
- \( A = \sqrt{28 \times (28-24) \times (28-7) \times (28-25)} \)
- \( A = \sqrt{28 \times 4 \times 21 \times 3} = \sqrt{7056} = 84 \) square meters.
Problem 3: Similar Triangles
Raul is 6 ft tall and he casts a shadow 5 ft long. He measures that the shadow cast by his school building is 30 ft long. How tall is the building?
- Using the properties of similar triangles:
- Height of Raul / Length of Raul's shadow = Height of building / Length of building's shadow
- \( \frac{6}{5} = \frac{h}{30} \)
- \( h = \frac{6 \times 30}{5} = 36 \) ft
Practice Problems
- The base of an isosceles triangle is 8 cm and its height is 5 cm. Find the area.
- A triangle has sides 9 cm, 12 cm, and 15 cm. Find the area using Heron's formula.
- The sides of a triangle are in the ratio 3:4:5. If the perimeter is 36 cm, find the lengths of the sides and the area.
Strategies and Tips
- Draw diagrams to visualize the problem.
- Use algebraic methods to set up and solve equations.
- Remember key formulas and properties, such as Heron's formula for area and the properties of similar triangles.
8. Advanced Worded Problems
Advanced word problems involving area and perimeter often require a deeper understanding of geometric principles, the ability to visualize complex shapes, and sometimes the integration of multiple formulas. Below are several examples and strategies to tackle these advanced problems step by step.
Example 1: Composite Shapes
Problem: A park consists of a rectangular playground that is 50 meters long and 30 meters wide, adjacent to a semicircular garden with a diameter of 30 meters. Find the total area of the park.
- Calculate the area of the rectangle:
- \( \text{Area}_{\text{rectangle}} = l \times w = 50 \, \text{m} \times 30 \, \text{m} = 1500 \, \text{m}^2 \)
- Calculate the area of the semicircle:
- Radius \( r = \frac{30 \, \text{m}}{2} = 15 \, \text{m} \)
- \( \text{Area}_{\text{semicircle}} = \frac{1}{2} \pi r^2 = \frac{1}{2} \pi (15 \, \text{m})^2 = \frac{1}{2} \pi (225 \, \text{m}^2) = 112.5 \pi \, \text{m}^2 \approx 353.43 \, \text{m}^2 \)
- Add the areas together to find the total area:
- \( \text{Total Area} = 1500 \, \text{m}^2 + 353.43 \, \text{m}^2 = 1853.43 \, \text{m}^2 \)
Example 2: Fencing Around an Irregular Shape
Problem: A garden has a shape composed of a rectangle and a triangle on one of its sides. The rectangle is 40 meters by 20 meters, and the triangle has a base of 20 meters and a height of 15 meters. Calculate the amount of fencing needed to enclose the garden.
- Calculate the perimeter of the rectangle:
- \( \text{Perimeter}_{\text{rectangle}} = 2(l + w) = 2(40 \, \text{m} + 20 \, \text{m}) = 120 \, \text{m} \)
- Calculate the sides of the triangle using the Pythagorean theorem:
- Each side of the triangle (legs are 15 m and 10 m each since the height splits the base in half): \( \sqrt{(10 \, \text{m})^2 + (15 \, \text{m})^2} = \sqrt{100 + 225} = \sqrt{325} \approx 18.03 \, \text{m} \)
- Add the triangle's base and the two sides to the rectangle's perimeter:
- \( \text{Perimeter}_{\text{triangle}} = 20 \, \text{m} + 2 \times 18.03 \, \text{m} = 56.06 \, \text{m} \)
- \( \text{Total Fencing Needed} = 120 \, \text{m} + 56.06 \, \text{m} = 176.06 \, \text{m} \)
Example 3: Finding the Area of an Irregular Polygon
Problem: A plot of land is shaped like an L, consisting of two rectangles. The larger rectangle is 40 meters by 30 meters, and the smaller rectangle is 20 meters by 10 meters, attached to the larger one at one corner. Find the total area.
- Calculate the area of both rectangles:
- \( \text{Area}_{\text{larger rectangle}} = 40 \, \text{m} \times 30 \, \text{m} = 1200 \, \text{m}^2 \)
- \( \text{Area}_{\text{smaller rectangle}} = 20 \, \text{m} \times 10 \, \text{m} = 200 \, \text{m}^2 \)
- Add the areas together to find the total area:
- \( \text{Total Area} = 1200 \, \text{m}^2 + 200 \, \text{m}^2 = 1400 \, \text{m}^2 \)
By breaking down complex shapes into simpler components and applying the appropriate formulas, advanced word problems involving area and perimeter can be systematically solved.

9. Strategies and Tips for Solving Worded Problems
Solving worded problems involving area and perimeter can be challenging, but with the right strategies and tips, you can master these problems step-by-step. Here are some effective strategies and tips to help you solve area and perimeter worded problems:
1. Understand the Problem
- Read Carefully: Read the problem thoroughly to understand what is being asked. Identify key information and underline important details.
- Visualize: Draw a diagram of the shape mentioned in the problem. This can help you see the relationship between different parts of the problem.
2. Identify Formulas and Key Information
- Know Your Formulas: Recall the relevant formulas for area and perimeter. For example:
- Perimeter of a rectangle: \(P = 2(l + w)\)
- Area of a rectangle: \(A = l \times w\)
- Perimeter of a square: \(P = 4s\)
- Area of a square: \(A = s^2\)
- Perimeter (circumference) of a circle: \(C = 2\pi r\)
- Area of a circle: \(A = \pi r^2\)
- Extract Key Information: Identify the given values (e.g., length, width, radius) and what you need to find.
3. Plan and Set Up the Equation
- Write Equations: Based on the given information and the formulas, set up the equation(s) you need to solve.
- Substitute Values: Substitute the known values into the equations.
4. Solve the Equations
- Perform Calculations: Carefully carry out the calculations needed to solve for the unknowns.
- Check Units: Ensure that your answer is in the correct units (e.g., square units for area, linear units for perimeter).
5. Verify Your Answer
- Double-Check: Verify your calculations and ensure that your answer makes sense in the context of the problem.
- Review the Problem: Re-read the problem to ensure you have answered all parts of the question.
6. Practice Regularly
- Practice Different Types: Solve a variety of worded problems involving different shapes and scenarios to build your skills.
- Collaborate and Discuss: Work with peers to discuss strategies and solutions to different problems. This can provide new insights and approaches.
Example Problem
Problem: A rectangular garden has a length of 10 meters and a width of 6 meters. What is the perimeter and area of the garden?
- Step 1: Identify the Formulas:
- Perimeter of a rectangle: \(P = 2(l + w)\)
- Area of a rectangle: \(A = l \times w\)
- Step 2: Substitute the Values:
- Perimeter: \(P = 2(10 + 6) = 2 \times 16 = 32\) meters
- Area: \(A = 10 \times 6 = 60\) square meters
By following these strategies and practicing regularly, you can become proficient in solving area and perimeter worded problems. Keep practicing and reviewing your work to improve your problem-solving skills.
10. Practice Exercises with Solutions
Practice exercises are crucial for mastering the concepts of area and perimeter. Below are some word problems along with detailed solutions to help you understand the step-by-step process involved in solving these problems.
Exercise 1: Rectangular Garden
A rectangular garden has a length of 15 meters and a width of 10 meters.
- Find the perimeter of the garden.
- Find the area of the garden.
Solution:
- Perimeter: \( P = 2(l + w) \)
- \( P = 2(15 + 10) = 2(25) = 50 \) meters
- Area: \( A = l \times w \)
- \( A = 15 \times 10 = 150 \) square meters
Exercise 2: Square Playground
A square playground has a side length of 20 meters.
- Find the perimeter of the playground.
- Find the area of the playground.
Solution:
- Perimeter: \( P = 4s \)
- \( P = 4 \times 20 = 80 \) meters
- Area: \( A = s^2 \)
- \( A = 20^2 = 400 \) square meters
Exercise 3: Circular Flower Bed
A circular flower bed has a radius of 7 meters.
- Find the circumference of the flower bed.
- Find the area of the flower bed.
Solution:
- Circumference: \( C = 2 \pi r \)
- \( C = 2 \pi \times 7 = 14 \pi \approx 43.98 \) meters
- Area: \( A = \pi r^2 \)
- \( A = \pi \times 7^2 = 49 \pi \approx 153.94 \) square meters
Exercise 4: Triangular Plot
A triangular plot has a base of 12 meters and a height of 9 meters.
- Find the area of the triangular plot.
- Find the perimeter of the triangle if the other two sides are 13 meters each.
Solution:
- Area: \( A = \frac{1}{2} \times \text{base} \times \text{height} \)
- \( A = \frac{1}{2} \times 12 \times 9 = 54 \) square meters
- Perimeter: \( P = \text{base} + \text{side1} + \text{side2} \)
- \( P = 12 + 13 + 13 = 38 \) meters
Exercise 5: Composite Shape
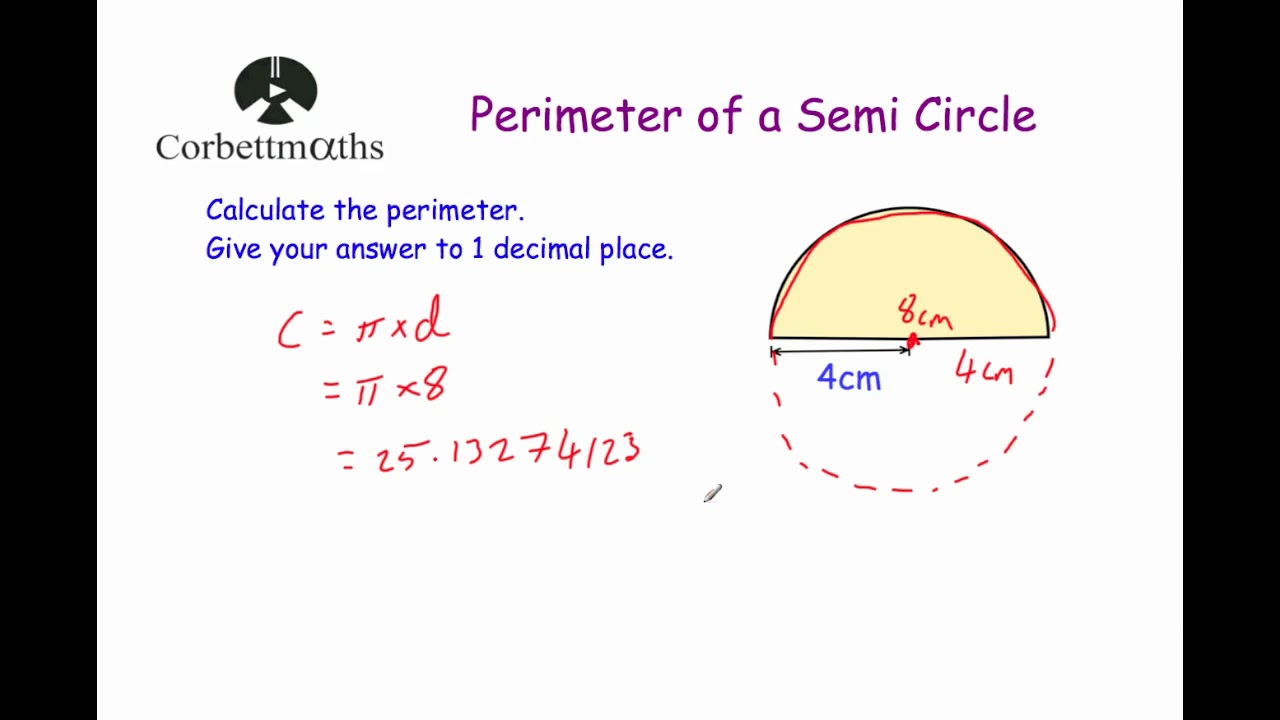
A composite shape consists of a rectangle and a semicircle on one of its shorter sides. The rectangle has a length of 10 meters and a width of 4 meters. The semicircle has a radius equal to the width of the rectangle.
- Find the perimeter of the composite shape.
- Find the area of the composite shape.
Solution:
- Perimeter of rectangle: \( P_{rect} = 2(l + w) = 2(10 + 4) = 28 \) meters
- Perimeter of semicircle: \( P_{semi} = \pi r \)
- \( P_{semi} = \pi \times 4 \approx 12.57 \) meters
- Total perimeter: \( P_{total} = 28 - 4 + 12.57 = 36.57 \) meters
- Area of rectangle: \( A_{rect} = l \times w = 10 \times 4 = 40 \) square meters
- Area of semicircle: \( A_{semi} = \frac{1}{2} \pi r^2 \)
- \( A_{semi} = \frac{1}{2} \pi \times 4^2 = 8 \pi \approx 25.13 \) square meters
- Total area: \( A_{total} = 40 + 25.13 = 65.13 \) square meters
These exercises should provide a solid foundation for understanding how to approach and solve word problems involving area and perimeter. Practice regularly to improve your problem-solving skills!
Video này hướng dẫn cách giải bài toán về diện tích và chu vi, cụ thể là tính chiều rộng của chuồng chó. Phù hợp cho học sinh và người học muốn cải thiện kỹ năng toán học của mình.
Bài toán diện tích và chu vi: chiều rộng của chuồng chó | Khan Academy
READ MORE:
Video này hướng dẫn cách giải bài toán về diện tích và chu vi, giúp người học nắm vững kiến thức và kỹ năng toán học cần thiết.
Bài toán Diện tích và Chu vi