Topic area perimeter and volume formulas: Discover the essential area, perimeter, and volume formulas for various geometric shapes. This comprehensive guide simplifies these fundamental concepts, providing clear formulas and practical examples. Whether you're a student, teacher, or math enthusiast, you'll find valuable insights to enhance your understanding and problem-solving skills. Dive in and master the basics of geometry with ease!
Table of Content
Geometry Formulas: Area, Perimeter, and Volume
This page provides essential formulas for calculating the area, perimeter, and volume of various geometric shapes. These formulas are fundamental in solving many geometry problems.
Basic Geometry Formulas
- Square:
- Area: \( A = a^2 \)
- Perimeter: \( P = 4a \)
- Rectangle:
- Area: \( A = l \times w \)
- Perimeter: \( P = 2(l + w) \)
- Triangle:
- Area: \( A = \frac{1}{2} \times b \times h \)
- Perimeter: \( P = a + b + c \)
- Circle:
- Area: \( A = \pi r^2 \)
- Circumference: \( C = 2\pi r \)
- Parallelogram:
- Area: \( A = b \times h \)
- Perimeter: \( P = 2(a + b) \)
- Trapezoid:
- Area: \( A = \frac{1}{2}h(b1 + b2) \)
- Perimeter: \( P = a + b1 + b2 + c \)
Solid Geometry Formulas
- Cube:
- Volume: \( V = a^3 \)
- Surface Area: \( SA = 6a^2 \)
- Rectangular Prism:
- Volume: \( V = l \times w \times h \)
- Surface Area: \( SA = 2(lw + lh + wh) \)
- Sphere:
- Volume: \( V = \frac{4}{3}\pi r^3 \)
- Surface Area: \( SA = 4\pi r^2 \)
- Cylinder:
- Volume: \( V = \pi r^2 h \)
- Surface Area: \( SA = 2\pi r(h + r) \)
- Cone:
- Volume: \( V = \frac{1}{3}\pi r^2 h \)
- Surface Area: \( SA = \pi r(r + \sqrt{h^2 + r^2}) \)
Examples
- Calculate the area of a square with a side length of 5 cm:
\( A = 5^2 = 25 \, \text{cm}^2 \)
- Find the volume of a cylinder with a radius of 3 cm and height of 7 cm:
\( V = \pi \times 3^2 \times 7 = 63\pi \, \text{cm}^3 \)
- Determine the surface area of a cube with a side length of 4 cm:
\( SA = 6 \times 4^2 = 96 \, \text{cm}^2 \)
Practice Problems
- If a rectangle has a width of 8 cm and a length of 15 cm, what is its area and perimeter?
- Calculate the volume and surface area of a sphere with a radius of 6 cm.
- What is the area of a triangle with a base of 10 cm and a height of 12 cm?
Use these formulas and examples to assist you in solving geometry problems related to area, perimeter, and volume.

Introduction
Understanding the formulas for area, perimeter, and volume is crucial for solving various geometric problems. These formulas allow you to calculate the dimensions and capacities of different shapes and objects, whether they are simple figures like rectangles and circles or more complex structures such as trapezoids and spheres. In this section, we will explore the fundamental formulas that are essential for mastering geometry.
- Area Formulas
- Area of a Square: \( A = a^2 \)
- Area of a Rectangle: \( A = l \times w \)
- Area of a Triangle: \( A = \frac{1}{2} \times b \times h \)
- Area of a Circle: \( A = \pi r^2 \)
- Area of a Trapezoid: \( A = \frac{1}{2} \times (b_1 + b_2) \times h \)
- Perimeter Formulas
- Perimeter of a Square: \( P = 4a \)
- Perimeter of a Rectangle: \( P = 2(l + w) \)
- Perimeter of a Triangle: \( P = a + b + c \)
- Circumference of a Circle: \( C = 2 \pi r \)
- Volume Formulas
- Volume of a Cube: \( V = a^3 \)
- Volume of a Rectangular Prism: \( V = l \times w \times h \)
- Volume of a Cylinder: \( V = \pi r^2 h \)
- Volume of a Sphere: \( V = \frac{4}{3} \pi r^3 \)
- Volume of a Cone: \( V = \frac{1}{3} \pi r^2 h \)
Basic Geometry Concepts
Geometry is a branch of mathematics that deals with shapes, sizes, the properties of space, and the relationships between objects. Understanding basic geometry concepts is essential for solving problems related to area, perimeter, and volume. Here, we will cover fundamental definitions and properties.
Points, Lines, and Angles
- Point: A location in space with no dimensions, represented by a dot.
- Line: A straight one-dimensional figure extending infinitely in both directions, with no curvature.
- Line Segment: A part of a line with two endpoints.
- Ray: A part of a line that starts at a point and extends infinitely in one direction.
- Angle: Formed by two rays with a common endpoint, measured in degrees.
Types of Angles
- Acute Angle: An angle less than 90°.
- Right Angle: An angle equal to 90°.
- Obtuse Angle: An angle greater than 90° but less than 180°.
- Straight Angle: An angle equal to 180°.
Basic Shapes and Their Properties
| Shape | Properties |
|---|---|
| Square |
|
| Rectangle |
|
| Triangle |
|
| Circle |
|
Solid Geometry
Solid geometry deals with three-dimensional objects. Here are the basic properties of some common 3D shapes:
- Cube:
- All sides are equal.
- Surface Area: \( SA = 6a^2 \)
- Volume: \( V = a^3 \)
- Rectangular Prism:
- Opposite faces are equal.
- Surface Area: \( SA = 2(lw + lh + wh) \)
- Volume: \( V = lwh \)
- Sphere:
- All points on the surface are equidistant from the center.
- Surface Area: \( SA = 4\pi r^2 \)
- Volume: \( V = \frac{4}{3}\pi r^3 \)
- Cylinder:
- Two parallel circular bases connected by a curved surface.
- Surface Area: \( SA = 2\pi r(h + r) \)
- Volume: \( V = \pi r^2h \)
Formulas for Perimeter
In geometry, the perimeter is the total length of the boundary of a two-dimensional shape. Here are the perimeter formulas for some common shapes:
Perimeter of Common Shapes
- Square: If each side of a square is \( s \), then the perimeter \( P \) is given by: \[ P = 4s \]
- Rectangle: If the length is \( l \) and the width is \( w \), then the perimeter \( P \) is: \[ P = 2l + 2w \]
- Triangle: For a triangle with sides \( a \), \( b \), and \( c \), the perimeter \( P \) is: \[ P = a + b + c \]
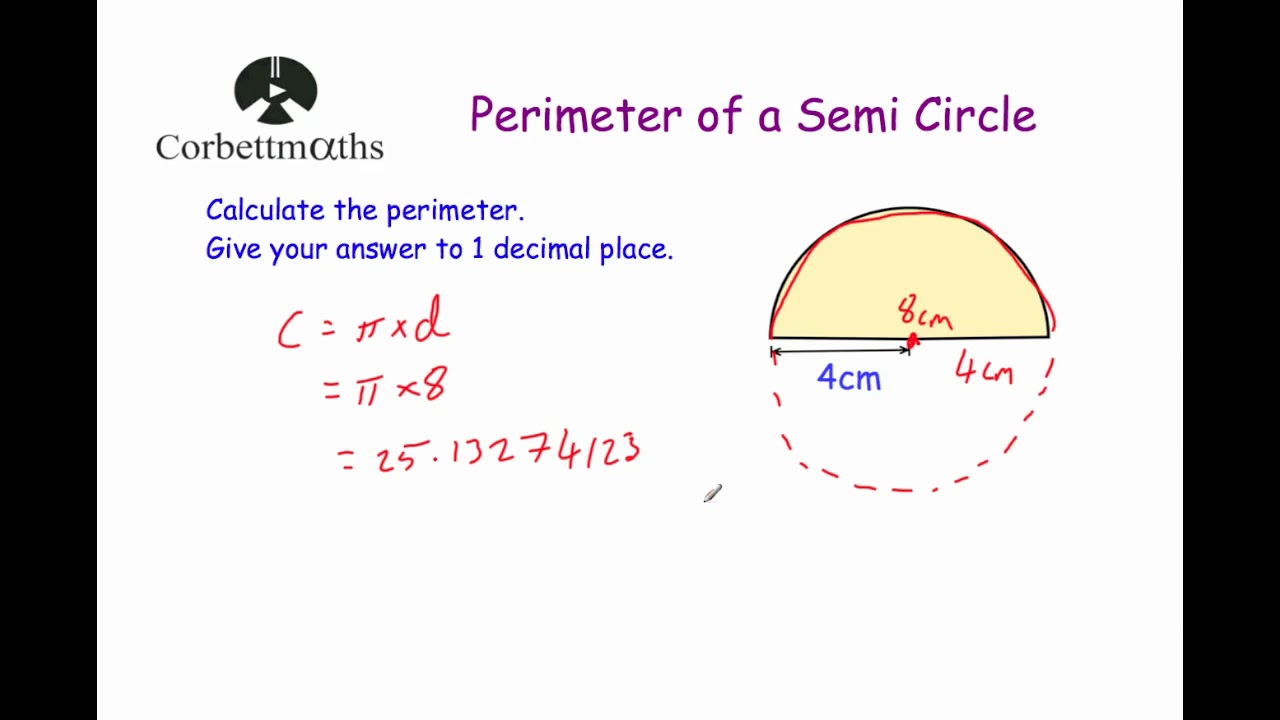
- Circle: The perimeter of a circle is known as the circumference. If the radius is \( r \), the circumference \( C \) is: \[ C = 2\pi r \]
- Parallelogram: If the lengths of the adjacent sides are \( a \) and \( b \), then the perimeter \( P \) is: \[ P = 2a + 2b \]
- Trapezoid: If the lengths of the four sides are \( a \), \( b \), \( c \), and \( d \), then the perimeter \( P \) is: \[ P = a + b + c + d \]
Special Cases and Examples
Let's consider some special cases and practical examples:
- Equilateral Triangle: For an equilateral triangle where all three sides are equal to \( a \): \[ P = 3a \]
- Regular Polygon: For a regular polygon with \( n \) sides each of length \( a \): \[ P = n \times a \]
Example Problems
- Find the perimeter of a rectangle with length 8 cm and width 5 cm.
Solution:
\[
P = 2 \times 8 + 2 \times 5 = 16 + 10 = 26 \text{ cm}
\] - A square garden has a side length of 15 meters. Calculate its perimeter.
Solution:
\[
P = 4 \times 15 = 60 \text{ meters}
\] - A circular park has a radius of 7 meters. Determine its circumference.
Solution:
\[
C = 2\pi \times 7 = 14\pi \approx 43.98 \text{ meters}
\]
Formulas for Area
Understanding the area of different shapes is fundamental in geometry. Below are the formulas for calculating the area of various common shapes:
Area of Common Shapes
- Square: The area of a square is given by the formula:
\( A = s^2 \)
where \( s \) is the length of one side of the square.
- Rectangle: The area of a rectangle is calculated by:
\( A = l \times w \)
where \( l \) is the length and \( w \) is the width.
- Triangle: The area of a triangle can be found using:
\( A = \frac{1}{2} \times b \times h \)
where \( b \) is the base and \( h \) is the height.
- Parallelogram: The area of a parallelogram is:
\( A = b \times h \)
where \( b \) is the base and \( h \) is the height.
- Trapezoid: The area of a trapezoid is:
\( A = \frac{1}{2} \times (b_1 + b_2) \times h \)
where \( b_1 \) and \( b_2 \) are the lengths of the two parallel sides and \( h \) is the height.
- Circle: The area of a circle is:
\( A = \pi r^2 \)
where \( r \) is the radius.
Complex Shapes and Composite Figures
For shapes that are more complex or are composed of multiple basic shapes, the following steps can be used:
- Break down the complex shape into simpler shapes whose areas can be calculated using basic formulas.
- Calculate the area of each simple shape.
- Sum the areas of the simple shapes to get the total area of the composite figure.
- For shapes with areas to be subtracted (e.g., a hole), calculate the area of the part to be subtracted and then subtract it from the total area.
For example, to find the area of a composite shape consisting of a rectangle with a semicircle on top:
- Calculate the area of the rectangle using \( A = l \times w \).
- Calculate the area of the semicircle using \( A = \frac{1}{2} \pi r^2 \), where \( r \) is the radius of the semicircle.
- Add the area of the rectangle and the area of the semicircle to get the total area.
| Shape | Formula |
|---|---|
| Square | \( A = s^2 \) |
| Rectangle | \( A = l \times w \) |
| Triangle | \( A = \frac{1}{2} \times b \times h \) |
| Parallelogram | \( A = b \times h \) |
| Trapezoid | \( A = \frac{1}{2} \times (b_1 + b_2) \times h \) |
| Circle | \( A = \pi r^2 \) |

Formulas for Volume
The volume of a shape measures the amount of space it occupies. Here are the formulas for finding the volume of various common three-dimensional shapes:
Volume of Common 3D Shapes
- Volume of a Cube: The volume \( V \) of a cube with side length \( a \) is given by: \[ V = a^3 \]
- Volume of a Rectangular Prism: The volume \( V \) of a rectangular prism with length \( l \), width \( w \), and height \( h \) is: \[ V = l \times w \times h \]
- Volume of a Cylinder: The volume \( V \) of a cylinder with base radius \( r \) and height \( h \) is: \[ V = \pi r^2 h \]
- Volume of a Cone: The volume \( V \) of a cone with base radius \( r \) and height \( h \) is: \[ V = \frac{1}{3} \pi r^2 h \]
- Volume of a Sphere: The volume \( V \) of a sphere with radius \( r \) is: \[ V = \frac{4}{3} \pi r^3 \]
Advanced Volume Calculations
For more complex shapes, the volume can often be found by dividing the shape into simpler parts, finding the volume of each part, and then adding them together. Some examples include:
- Volume of a Pyramid: The volume \( V \) of a pyramid with base area \( B \) and height \( h \) is: \[ V = \frac{1}{3} B h \]
- Volume of Composite Shapes: To find the volume of a composite shape, sum the volumes of the individual components: \[ V_{\text{total}} = V_1 + V_2 + \ldots + V_n \]
Practice Problems and Solutions
Below are a few practice problems to help reinforce the concepts:
- Problem 1: Find the volume of a cylinder with a radius of 4 cm and a height of 10 cm.
Solution: \[ V = \pi r^2 h = \pi (4)^2 (10) = 160 \pi \approx 502.65 \, \text{cm}^3 \] - Problem 2: Calculate the volume of a cone with a base radius of 3 cm and a height of 9 cm.
Solution: \[ V = \frac{1}{3} \pi r^2 h = \frac{1}{3} \pi (3)^2 (9) = 27 \pi \approx 84.82 \, \text{cm}^3 \] - Problem 3: A sphere has a diameter of 10 cm. What is its volume?
Solution: \[ V = \frac{4}{3} \pi r^3 = \frac{4}{3} \pi (5)^3 = \frac{500}{3} \pi \approx 523.60 \, \text{cm}^3 \]
Surface Area Calculations
Surface area is the total area that the surface of a 3-dimensional object occupies. It's essential in various fields such as architecture, engineering, and manufacturing. Understanding how to calculate surface area is crucial for designing and analyzing objects accurately.
To calculate the surface area of different 3D shapes, specific formulas are required. Here, we'll explore some common 3D shapes and their corresponding surface area formulas:
- Cube: To find the surface area of a cube, you can use the formula:
- Rectangular Prism: For a rectangular prism, the surface area can be calculated using:
- Sphere: The surface area of a sphere is determined by:
- Cylinder: When dealing with a cylinder, the surface area formula is:
- Cone: Lastly, for a cone, the surface area can be found using:
Surface Area = 6 * (side length)^2
Surface Area = 2 * (length * width + width * height + height * length)
Surface Area = 4 * π * (radius)^2
Surface Area = 2 * π * radius * (radius + height)
Surface Area = π * radius * (radius + slant height)
Remember to substitute the appropriate values for the dimensions into these formulas to obtain accurate results. Additionally, it's essential to understand the concept of each shape's surface area formula to apply it correctly in real-world scenarios.
Applications and Practice Problems
Understanding area, perimeter, and volume formulas is not only important for academic purposes but also for real-world applications. Here are some practical scenarios where these concepts are utilized:
- Construction and Architecture: Architects and builders frequently use area, perimeter, and volume calculations to design and construct buildings, rooms, and structures. These calculations help determine the amount of materials needed and ensure proper dimensions.
- Landscaping: Landscapers use these formulas to plan and execute outdoor projects such as garden layouts, lawn installations, and patio constructions. Calculating areas and perimeters of various sections of a landscape helps in optimizing space and budget.
- Engineering: Engineers rely on area, perimeter, and volume calculations in various fields, including civil, mechanical, and electrical engineering. Whether designing bridges, machinery, or electronic components, understanding these concepts is fundamental.
- Finance and Economics: Analysts and economists often utilize these formulas to assess property values, calculate land or property taxes, and estimate costs for construction projects. These calculations play a significant role in financial decision-making.
Now, let's delve into some practice problems to reinforce your understanding of these concepts:
- Calculate the perimeter of a rectangular garden with dimensions 20 meters by 30 meters.
- Find the area of a circle with a radius of 5 centimeters.
- Determine the volume of a cube with edges measuring 8 inches.
- Compute the surface area of a cylinder with a radius of 6 meters and a height of 10 meters.
These practice problems will help you apply the formulas learned and enhance your problem-solving skills in geometry and mathematics.
Additional Resources
To further enhance your understanding of geometry concepts related to area, perimeter, and volume, the following resources are highly recommended:
- Online Calculators: Utilize online calculators for quick computations of area, perimeter, and volume. Some reliable options include:
- Tutorial Videos: Visual learners can benefit from video tutorials that explain geometry concepts in a step-by-step manner. Check out these channels:
- Interactive Tools: Explore interactive tools and apps that provide hands-on practice with geometry problems.
- Books and E-books: Consider reading comprehensive books on geometry for a deeper understanding. Some recommended titles include:
- "Geometry For Dummies" by Mark Ryan
- "The Complete Book of Geometry" by School Specialty Publishing
- Practice Worksheets: Download and print practice worksheets to test your knowledge and skills. Websites offering free worksheets include:
- Forums and Study Groups: Join online forums and study groups to discuss problems and solutions with peers.

Giải Thích Chu Vi, Diện Tích và Thể Tích | Toán Học với Thầy J
READ MORE:
Chu Vi và Diện Tích: Những Kiến Thức Cơ Bản | Chu Vi, Diện Tích và Thể Tích | Hình Học | Khan Academy