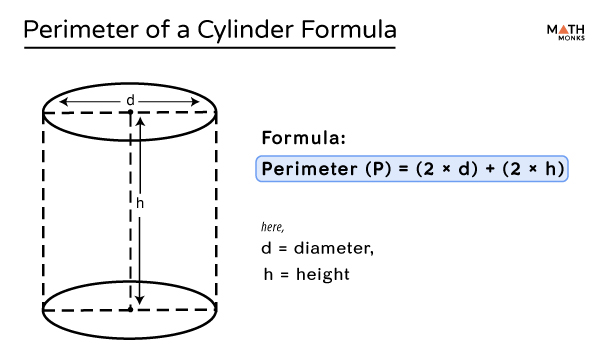
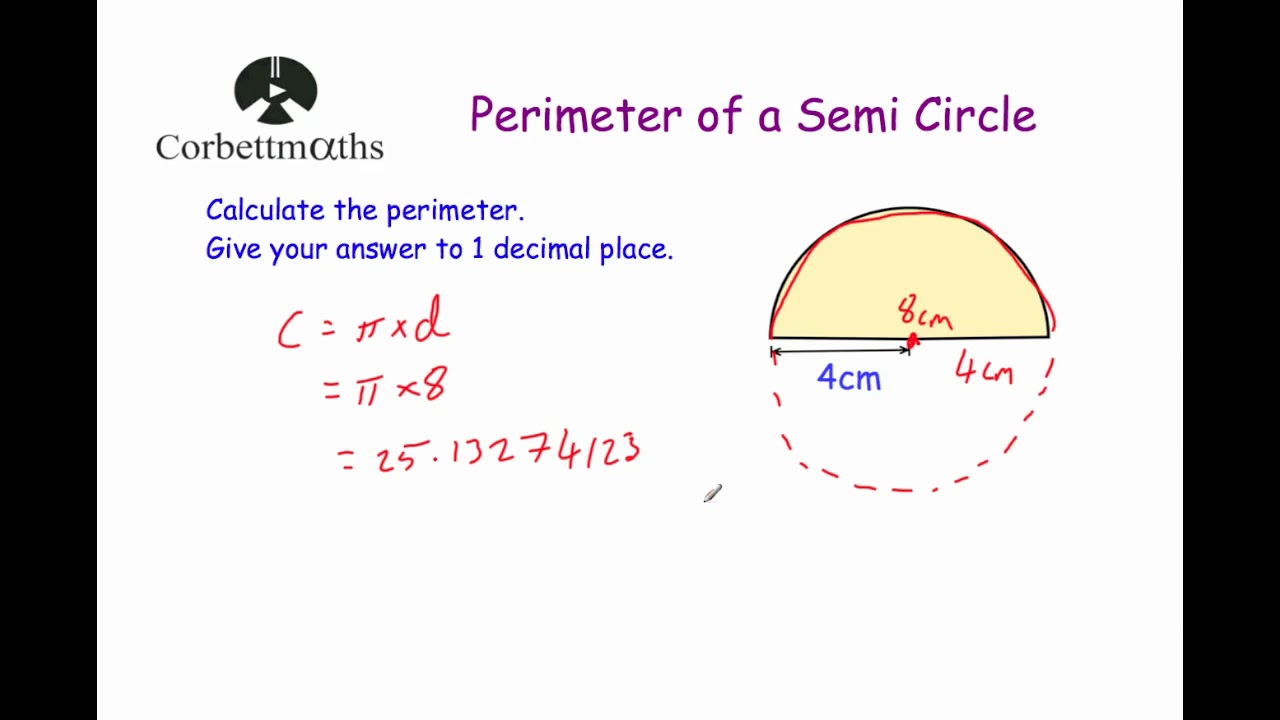
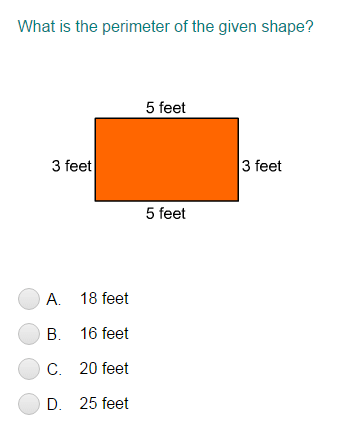
Topic area and perimeter quiz: Looking to sharpen your geometry skills? Our comprehensive area and perimeter quiz is designed to challenge and educate. With a variety of problems, tips, and real-life applications, you'll master these essential concepts in no time. Dive in now and see how much you can learn and improve!
Table of Content
- Area and Perimeter Quiz
- Introduction to Area and Perimeter
- Basic Concepts and Definitions
- Formulas for Calculating Area and Perimeter
- Area and Perimeter of Common Shapes
- Rectangles and Squares
- Triangles
- Circles
- Polygons
- Complex Shapes
- Real-Life Applications of Area and Perimeter
- Word Problems Involving Area and Perimeter
- Interactive Quizzes and Practice Problems
- Multiple Choice Questions
- Fill-in-the-Blank Questions
- True or False Questions
- Step-by-Step Solutions and Explanations
- Tips and Tricks for Solving Area and Perimeter Problems
- Common Mistakes to Avoid
- YOUTUBE: Xem video 'Câu Đố Toán Học - Chu Vi (Phần 1)' để học và kiểm tra kiến thức về chu vi trong toán học.
Area and Perimeter Quiz
Test your understanding of geometric concepts with our comprehensive quizzes on area and perimeter. These quizzes cover a range of shapes, including squares, rectangles, triangles, and circles. Practice your skills with interactive questions and enhance your knowledge of these fundamental mathematical properties.
Key Concepts
- Area: The measure of space covered by a two-dimensional shape. Common formulas include:
- Rectangle: \( \text{Area} = l \times w \)
- Square: \( \text{Area} = s^2 \)
- Triangle: \( \text{Area} = \frac{1}{2} \times b \times h \)
- Circle: \( \text{Area} = \pi r^2 \)
- Perimeter: The total length around a two-dimensional shape. Common formulas include:
- Rectangle: \( \text{Perimeter} = 2(l + w) \)
- Square: \( \text{Perimeter} = 4s \)
- Triangle: \( \text{Perimeter} = a + b + c \)
- Circle (Circumference): \( \text{Circumference} = 2\pi r \)
Sample Quiz Questions
What is the area of a rectangle with a length of 5 units and a width of 3 units?
- A) 15 square units
- B) 8 square units
- C) 12 square units
- D) 10 square units
Calculate the perimeter of a square with a side length of 4 units.
- A) 16 units
- B) 12 units
- C) 8 units
- D) 20 units
A circle has a radius of 7 units. What is its area?
- A) \( 49\pi \) square units
- B) \( 14\pi \) square units
- C) \( 7\pi \) square units
- D) \( 28\pi \) square units
Find the perimeter of a triangle with sides measuring 3 units, 4 units, and 5 units.
- A) 12 units
- B) 10 units
- C) 15 units
- D) 9 units
Practice Areas
| Shape | Area Formula | Perimeter Formula |
|---|---|---|
| Rectangle | \( A = l \times w \) | \( P = 2(l + w) \) |
| Square | \( A = s^2 \) | \( P = 4s \) |
| Triangle | \( A = \frac{1}{2} \times b \times h \) | \( P = a + b + c \) |
| Circle | \( A = \pi r^2 \) | \( C = 2\pi r \) |
Why Study Area and Perimeter?
Understanding area and perimeter is essential for solving real-world problems, from calculating the amount of paint needed to cover a wall to determining the length of fencing required for a garden. These concepts are foundational in geometry and help build a deeper understanding of more complex mathematical topics.
Use our quizzes to reinforce your learning and challenge your skills in area and perimeter calculations. Get started today and master the basics of geometry!
READ MORE:
Introduction to Area and Perimeter
Understanding the concepts of area and perimeter is fundamental in geometry. These measurements are not only crucial in mathematics but also have practical applications in everyday life, such as in construction, crafting, and various forms of design.
Area is defined as the amount of space inside a two-dimensional shape. It is measured in square units (e.g., square meters, square inches). The formula to calculate the area varies depending on the shape:
- Rectangle: \( \text{Area} = \text{length} \times \text{width} \)
- Triangle: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
- Circle: \( \text{Area} = \pi \times \text{radius}^2 \)
Perimeter is the total distance around the edge of a shape. It is measured in linear units (e.g., meters, inches). The formula for perimeter also depends on the shape:
- Rectangle: \( \text{Perimeter} = 2 \times (\text{length} + \text{width}) \)
- Triangle: \( \text{Perimeter} = \text{side}_1 + \text{side}_2 + \text{side}_3 \)
- Circle (Circumference): \( \text{Perimeter} = 2 \times \pi \times \text{radius} \)
Both area and perimeter are essential for solving various geometric problems and have numerous practical applications. For example, when buying materials to build a fence, knowing the perimeter helps determine the amount of fencing needed, while knowing the area is crucial for purchasing enough material to cover a surface.
By understanding these basic concepts, you can solve a wide range of mathematical problems and apply these skills in real-world scenarios.
Basic Concepts and Definitions
Understanding area and perimeter is fundamental in geometry. Below, we define these key concepts and provide basic formulas used to calculate them for common shapes.
-
Perimeter
The perimeter of a shape is the total distance around its edges. It is calculated by summing the lengths of all sides of the shape. For example, the perimeter of a rectangle is calculated as:
\[ P = 2l + 2w \]
where \( l \) is the length and \( w \) is the width.
-
Area
The area of a shape is the amount of space enclosed within its boundaries. Different shapes have different area formulas. For example:
- Rectangle: \[ A = l \times w \]
- Square: \[ A = s^2 \]
- Triangle: \[ A = \frac{1}{2} \times b \times h \]
- Circle: \[ A = \pi r^2 \]
Examples
Here are some practical examples to illustrate these concepts:
- To find the perimeter of a rectangle with length 7 cm and width 5 cm:
- To find the area of a square with side length 4 cm:
- To find the area of a triangle with base 8 cm and height 5 cm:
\[ P = 2(7) + 2(5) = 14 + 10 = 24 \text{ cm} \]
\[ A = 4^2 = 16 \text{ cm}^2 \]
\[ A = \frac{1}{2} \times 8 \times 5 = 20 \text{ cm}^2 \]
Units of Measurement
It is important to note that perimeter is measured in linear units (e.g., cm, m, in) while area is measured in square units (e.g., cm², m², in²).
Applications
These concepts are used in various real-life applications such as determining the amount of material needed for construction, fabric for clothing, and land for agricultural purposes.
Formulas for Calculating Area and Perimeter
Understanding the formulas for calculating area and perimeter is crucial for solving geometry problems. Below are the formulas for various common shapes:
Rectangle
- Area (A): \( A = l \times w \)
where \( l \) is the length and \( w \) is the width. - Perimeter (P): \( P = 2(l + w) \)
Square
- Area (A): \( A = s^2 \)
where \( s \) is the side length. - Perimeter (P): \( P = 4s \)
Triangle
- Area (A): \( A = \frac{1}{2} \times b \times h \)
where \( b \) is the base and \( h \) is the height. - Perimeter (P): \( P = a + b + c \)
where \( a \), \( b \), and \( c \) are the lengths of the sides.
Circle
- Area (A): \( A = \pi r^2 \)
where \( r \) is the radius. - Perimeter (Circumference, C): \( C = 2 \pi r \)
Parallelogram
- Area (A): \( A = b \times h \)
where \( b \) is the base and \( h \) is the height. - Perimeter (P): \( P = 2(a + b) \)
where \( a \) and \( b \) are the lengths of the sides.
Trapezoid
- Area (A): \( A = \frac{1}{2} \times (b_1 + b_2) \times h \)
where \( b_1 \) and \( b_2 \) are the lengths of the parallel sides, and \( h \) is the height. - Perimeter (P): \( P = a + b_1 + b_2 + c \)
where \( a \) and \( c \) are the lengths of the non-parallel sides.
Regular Polygon
- Area (A): \( A = \frac{1}{4} n s^2 \cot(\frac{\pi}{n}) \)
where \( n \) is the number of sides, and \( s \) is the side length. - Perimeter (P): \( P = n \times s \)
| Shape | Area Formula | Perimeter Formula |
|---|---|---|
| Rectangle | \( A = l \times w \) | \( P = 2(l + w) \) |
| Square | \( A = s^2 \) | \( P = 4s \) |
| Triangle | \( A = \frac{1}{2} \times b \times h \) | \( P = a + b + c \) |
| Circle | \( A = \pi r^2 \) | \( C = 2 \pi r \) |
| Parallelogram | \( A = b \times h \) | \( P = 2(a + b) \) |
| Trapezoid | \( A = \frac{1}{2} \times (b_1 + b_2) \times h \) | \( P = a + b_1 + b_2 + c \) |
| Regular Polygon | \( A = \frac{1}{4} n s^2 \cot(\frac{\pi}{n}) \) | \( P = n \times s \) |
These formulas form the foundation for solving various geometric problems related to area and perimeter. Understanding and memorizing these can help you tackle a wide range of questions effectively.
Area and Perimeter of Common Shapes
Understanding the area and perimeter of common shapes is crucial in geometry. Below are the formulas and explanations for calculating the area and perimeter of various common shapes:
Rectangles
- Perimeter: The perimeter \(P\) of a rectangle is calculated as: \[ P = 2(l + w) \] where \(l\) is the length and \(w\) is the width.
- Area: The area \(A\) of a rectangle is given by: \[ A = l \times w \]
Squares
- Perimeter: The perimeter \(P\) of a square is: \[ P = 4s \] where \(s\) is the side length.
- Area: The area \(A\) of a square is: \[ A = s^2 \]
Triangles
- Perimeter: The perimeter \(P\) of a triangle is the sum of its sides: \[ P = a + b + c \] where \(a\), \(b\), and \(c\) are the lengths of the sides.
- Area: The area \(A\) of a triangle can be calculated using the base \(b\) and height \(h\): \[ A = \frac{1}{2} b \times h \]
Circles
- Circumference: The circumference \(C\) of a circle is: \[ C = 2\pi r \] where \(r\) is the radius.
- Area: The area \(A\) of a circle is: \[ A = \pi r^2 \]
Polygons
- Perimeter: The perimeter \(P\) of a polygon is the sum of the lengths of its sides: \[ P = \sum_{i=1}^{n} s_i \] where \(s_i\) are the lengths of the sides and \(n\) is the number of sides.
- Area: The area of regular polygons can be calculated using specific formulas depending on the number of sides and the length of each side.
Complex Shapes
For more complex shapes, the area and perimeter can be found by breaking the shape into simpler parts, calculating the area and perimeter of each part, and then summing these values.
Understanding these basic formulas and concepts is essential for solving more complex geometric problems and applying these calculations to real-world scenarios, such as determining the amount of material needed for a construction project or calculating the distance around a property.

Rectangles and Squares
Understanding the area and perimeter of rectangles and squares is fundamental in geometry. Here, we will explore the formulas and methods to calculate these measurements, along with practical examples and practice problems.
Basic Definitions
- Rectangle: A four-sided polygon with opposite sides equal and all angles right angles (90 degrees).
- Square: A special type of rectangle where all four sides are of equal length and all angles are right angles.
Formulas
To calculate the area and perimeter of rectangles and squares, we use the following formulas:
- Area of a Rectangle: \( A = l \times w \)
- Perimeter of a Rectangle: \( P = 2l + 2w \) or \( P = 2(l + w) \)
- Area of a Square: \( A = s^2 \)
- Perimeter of a Square: \( P = 4s \)
Example Calculations
- Rectangle Example:
Given a rectangle with length \( l = 8 \) units and width \( w = 5 \) units:
Area: \( A = l \times w = 8 \times 5 = 40 \) square units
Perimeter: \( P = 2(l + w) = 2(8 + 5) = 2 \times 13 = 26 \) units
- Square Example:
Given a square with side length \( s = 4 \) units:
Area: \( A = s^2 = 4^2 = 16 \) square units
Perimeter: \( P = 4s = 4 \times 4 = 16 \) units
Practice Problems
- Find the area and perimeter of a rectangle with length 10 units and width 7 units.
- Calculate the area and perimeter of a square with side length 6 units.
- A rectangle has a perimeter of 24 units and a length of 7 units. Find its width and area.
Interactive Quiz
Test your knowledge with the following interactive quiz:
- What is the perimeter of a rectangle with a length of 12 units and a width of 5 units?
- If the side length of a square is doubled, how does the area change?
Use these concepts and practice problems to reinforce your understanding of calculating the area and perimeter of rectangles and squares.
Triangles
The area and perimeter of triangles are essential concepts in geometry. Understanding these formulas allows us to solve various practical problems.
Basic Definitions
- Base (b): One side of the triangle, typically the bottom side when drawn horizontally.
- Height (h): The perpendicular distance from the base to the opposite vertex.
- Sides (a, b, c): The lengths of the triangle's edges.
Area of a Triangle
The area (A) of a triangle can be calculated using the formula:
\[
A = \frac{1}{2} \times b \times h
\]
Where \( b \) is the base and \( h \) is the height.
Example Calculation
For a triangle with a base of 5 units and a height of 4 units:
\[
A = \frac{1}{2} \times 5 \times 4 = 10 \text{ square units}
\]
Perimeter of a Triangle
The perimeter (P) of a triangle is the sum of the lengths of its sides:
\[
P = a + b + c
\]
Where \( a \), \( b \), and \( c \) are the lengths of the triangle's sides.
Example Calculation
For a triangle with sides of 3 units, 4 units, and 5 units:
\[
P = 3 + 4 + 5 = 12 \text{ units}
\]
Special Types of Triangles
Equilateral Triangle
An equilateral triangle has all three sides equal and all angles equal to 60 degrees. The area can be calculated using:
\[
A = \frac{\sqrt{3}}{4} \times a^2
\]
Where \( a \) is the length of a side.
Example Calculation
For an equilateral triangle with side length 6 units:
\[
A = \frac{\sqrt{3}}{4} \times 6^2 = \frac{\sqrt{3}}{4} \times 36 = 9\sqrt{3} \approx 15.59 \text{ square units}
\]
Isosceles Triangle
An isosceles triangle has two sides of equal length. If the equal sides are \( a \) and the base is \( b \), the height can be calculated as:
\[
h = \sqrt{a^2 - \left(\frac{b}{2}\right)^2}
\]
Example Calculation
For an isosceles triangle with sides of 5 units and base of 6 units:
\[
h = \sqrt{5^2 - \left(\frac{6}{2}\right)^2} = \sqrt{25 - 9} = \sqrt{16} = 4 \text{ units}
\]
The area then is:
\[
A = \frac{1}{2} \times 6 \times 4 = 12 \text{ square units}
\]
Scalene Triangle
A scalene triangle has all sides of different lengths. The area can be calculated using Heron's formula:
\[
s = \frac{a + b + c}{2}
\]
\[
A = \sqrt{s(s - a)(s - b)(s - c)}
\]
Example Calculation
For a triangle with sides 3 units, 4 units, and 5 units:
\[
s = \frac{3 + 4 + 5}{2} = 6
\]
\[
A = \sqrt{6(6 - 3)(6 - 4)(6 - 5)} = \sqrt{6 \times 3 \times 2 \times 1} = \sqrt{36} = 6 \text{ square units}
\]
Interactive Quiz
Test your understanding of the area and perimeter of triangles with the following questions:
- What is the area of a triangle with a base of 8 units and a height of 5 units?
- If a triangle has sides of 7 units, 24 units, and 25 units, what is its perimeter?
- Calculate the area of an equilateral triangle with side length 10 units.
Circles
The circle is a fundamental shape in geometry, characterized by its perfectly round shape and constant radius from the center to any point on its circumference. Understanding the properties of circles is essential for calculating both the area and the perimeter (circumference).
Basic Definitions
- Radius (r): The distance from the center of the circle to any point on its circumference.
- Diameter (d): The distance across the circle, passing through the center. It is twice the radius, \(d = 2r\).
- Circumference (C): The total distance around the circle.
- Area (A): The amount of space enclosed within the circle.
Formulas
The key formulas for calculating the area and circumference of a circle are:
- Circumference: \(C = 2\pi r\) or \(C = \pi d\)
- Area: \(A = \pi r^2\)
Steps to Calculate the Area and Circumference
- Measure or identify the radius (r) or diameter (d) of the circle.
- Use the circumference formula if you need to find the perimeter:
- If you have the radius: \(C = 2\pi r\)
- If you have the diameter: \(C = \pi d\)
- Use the area formula if you need to find the space inside the circle:
- Always use the radius in the formula: \(A = \pi r^2\)
Example Problems
Example 1: Find the circumference and area of a circle with a radius of 5 cm.
- Circumference: \(C = 2\pi \times 5 = 10\pi \approx 31.42 \text{ cm}\)
- Area: \(A = \pi \times 5^2 = 25\pi \approx 78.54 \text{ cm}^2\)
Example 2: Find the circumference and area of a circle with a diameter of 10 cm.
- Circumference: \(C = \pi \times 10 = 10\pi \approx 31.42 \text{ cm}\)
- Area: First, find the radius: \(r = \frac{d}{2} = 5 \text{ cm}\), then \(A = \pi \times 5^2 = 25\pi \approx 78.54 \text{ cm}^2\)
Interactive Quizzes
To test your understanding of circles, try these interactive quizzes:
Polygons
A polygon is a 2-dimensional shape with straight sides. Polygons can have any number of sides, but the sides must be straight and the shape must be closed. Some common polygons include triangles, quadrilaterals, pentagons, hexagons, etc.
Basic Definitions
- Vertices: The corners where the sides of a polygon meet.
- Edges: The sides of a polygon.
- Interior Angles: The angles inside the polygon.
Formulas for Perimeter and Area
The perimeter of a polygon is the total distance around the outside, while the area is the amount of space enclosed within the polygon. The formulas vary depending on the type of polygon.
Regular Polygons
A regular polygon has all sides and angles equal.
- Perimeter (P): \( P = n \times s \) where \( n \) is the number of sides and \( s \) is the length of each side.
- Area (A): \( A = \frac{1}{4} n s^2 \cot(\frac{\pi}{n}) \)
Irregular Polygons
For irregular polygons, the perimeter is still the sum of all side lengths, but the area calculation depends on the specific shape. Here’s a general method using coordinates (xi, yi).
Area (A):
Examples of Common Polygons
- Triangle: \( P = a + b + c \), \( A = \frac{1}{2} \times b \times h \)
- Rectangle: \( P = 2(l + w) \), \( A = l \times w \)
- Square: \( P = 4s \), \( A = s^2 \)
- Pentagon: \( P = 5s \), \( A = \frac{1}{4} \sqrt{5(5 + 2\sqrt{5})} s^2 \)
- Hexagon: \( P = 6s \), \( A = \frac{3 \sqrt{3}}{2} s^2 \)
Interactive Practice Problems
Test your knowledge with these practice problems:
- Calculate the perimeter and area of a regular pentagon with a side length of 4 cm.
- If the coordinates of a quadrilateral are (1,1), (4,1), (4,5), and (1,5), find the area.
- Determine the perimeter of an irregular hexagon with sides measuring 2 cm, 3 cm, 4 cm, 5 cm, 6 cm, and 7 cm.
Understanding these concepts will help you solve various polygon-related problems efficiently. Happy learning!

Complex Shapes
Calculating the area and perimeter of complex shapes often involves breaking down the shape into simpler components such as rectangles, triangles, circles, and other polygons. Here's a step-by-step guide to help you navigate through these calculations:
1. Decomposing Complex Shapes
To find the area and perimeter of a complex shape, start by decomposing it into simpler shapes whose area and perimeter formulas you already know. For example:
- Rectangles
- Triangles
- Circles
- Polygons
Identify these smaller shapes within the complex shape and outline them clearly.
2. Calculating Area
Once you've decomposed the complex shape, calculate the area of each smaller shape using the appropriate formulas:
- Rectangle: \( \text{Area} = \text{length} \times \text{width} \)
- Triangle: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \)
- Circle: \( \text{Area} = \pi r^2 \)
- Polygon: Use specific formulas based on the type of polygon, such as the formula for the area of a regular polygon.
Add the areas of all the smaller shapes to get the total area of the complex shape.
3. Calculating Perimeter
For the perimeter, add up the outer sides of the complex shape. Be careful not to double-count any sides shared by two shapes. Here's how you can approach it:
- List all the outer edges of the shape.
- Measure each edge accurately.
- Add up all the outer edge lengths to get the total perimeter.
4. Example Problem
Consider a complex shape composed of a rectangle and a semicircle on top:
- Rectangle dimensions: 10 units (length) and 4 units (width).
- Semicircle radius: 2 units (half of the width of the rectangle).
Step-by-Step Solution:
- Calculate the area of the rectangle: \( 10 \times 4 = 40 \) square units.
- Calculate the area of the semicircle: \( \frac{1}{2} \pi r^2 = \frac{1}{2} \pi (2^2) = 2\pi \) square units.
- Add the areas: \( 40 + 2\pi \approx 40 + 6.28 = 46.28 \) square units.
- Calculate the perimeter:
- Rectangle perimeter excluding the shared width: \( 10 + 10 + 4 = 24 \) units.
- Semicircle circumference: \( \pi r = \pi \times 2 = 6.28 \) units.
- Add the perimeters: \( 24 + 6.28 = 30.28 \) units.
5. Tips and Tricks
- Draw the shape and label all dimensions clearly.
- Double-check calculations for accuracy.
- Use a calculator for complex arithmetic involving \(\pi\).
By following these steps, you can confidently tackle area and perimeter problems involving complex shapes.
Real-Life Applications of Area and Perimeter
Understanding area and perimeter is essential in various real-life scenarios. These concepts are not just confined to the classroom; they have practical applications in everyday life.
- Home Improvement and Interior Design:
When renovating a house, you need to calculate the area of walls and floors to buy the correct amount of paint, wallpaper, or flooring. For example, if you need to paint a room, you would calculate the area of each wall and add them up to know how much paint to purchase.
- Landscaping and Gardening:
Gardeners use the concepts of area and perimeter to plan the layout of gardens, flower beds, and lawns. Calculating the perimeter helps in determining the length of fencing required, while the area is used to estimate the amount of soil, mulch, or sod needed.
- Construction:
Builders and architects use these measurements to create building plans and ensure efficient use of materials. For example, knowing the area of a plot of land is essential when planning the layout of a new building or when dividing land into plots for development.
- Sports Fields:
In sports, the dimensions of fields and courts are crucial. Calculating the area ensures that the playing surface meets regulation sizes, while the perimeter can help in planning spectator areas and security fencing.
- Fashion and Tailoring:
Designers and tailors need to know the area of fabric required to create clothing patterns. Accurate measurements ensure that enough material is available without excessive waste.
- Real Estate:
Real estate agents and buyers often look at the area of properties to compare sizes and value. The area helps in determining the price of the land and the usability of space.
Examples of Calculations
- Painting a Room:
If a room has four walls, each 10 feet wide and 8 feet high, the total wall area to be painted is calculated as:
\[
\text{Total Area} = 4 \times (10 \, \text{ft} \times 8 \, \text{ft}) = 320 \, \text{sq ft}
\] - Fencing a Garden:
If a rectangular garden is 30 feet long and 20 feet wide, the perimeter is:
\[
\text{Perimeter} = 2 \times (30 \, \text{ft} + 20 \, \text{ft}) = 100 \, \text{ft}
\]
This tells you the length of the fencing material needed. - Buying Carpet:
To carpet a room that is 15 feet by 12 feet, the area is:
\[
\text{Area} = 15 \, \text{ft} \times 12 \, \text{ft} = 180 \, \text{sq ft}
\]
This ensures you purchase the correct amount of carpet.
Word Problems Involving Area and Perimeter
Word problems involving area and perimeter require understanding the concepts and applying the appropriate formulas to solve real-world scenarios. Here are some examples and steps to solve these types of problems:
-
Example 1: Fencing a Garden
A gardener wants to fence a rectangular garden that measures 10 meters by 5 meters. How much fencing material is needed?
- Identify the formula for perimeter: \( P = 2l + 2w \)
- Plug in the given values: \( l = 10 \) meters, \( w = 5 \) meters
- Calculate the perimeter: \( P = 2(10) + 2(5) = 20 + 10 = 30 \) meters
- The gardener needs 30 meters of fencing material.
-
Example 2: Painting a Wall
A painter needs to paint a rectangular wall that is 8 feet high and 12 feet wide. What is the area to be painted?
- Identify the formula for area: \( A = l \times w \)
- Plug in the given values: \( l = 8 \) feet, \( w = 12 \) feet
- Calculate the area: \( A = 8 \times 12 = 96 \) square feet
- The painter needs to cover 96 square feet of wall.
-
Example 3: Carpeting a Room
A room measures 15 feet by 20 feet. How much carpet is needed to cover the floor?
- Identify the formula for area: \( A = l \times w \)
- Plug in the given values: \( l = 15 \) feet, \( w = 20 \) feet
- Calculate the area: \( A = 15 \times 20 = 300 \) square feet
- The carpet required is 300 square feet.
-
Example 4: Finding Missing Dimensions
A rectangular plot has a perimeter of 60 meters, and its length is 20 meters. What is the width of the plot?
- Identify the formula for perimeter: \( P = 2l + 2w \)
- Plug in the given values: \( P = 60 \) meters, \( l = 20 \) meters
- Solve for the width: \( 60 = 2(20) + 2w \)
- Simplify the equation: \( 60 = 40 + 2w \)
- Subtract 40 from both sides: \( 20 = 2w \)
- Divide by 2: \( w = 10 \) meters
- The width of the plot is 10 meters.
These examples demonstrate how to apply area and perimeter formulas to solve practical problems. Understanding these concepts can help in various real-life situations, such as home improvement projects and construction planning.
Interactive Quizzes and Practice Problems
Interactive quizzes and practice problems are an excellent way to reinforce understanding of area and perimeter concepts. These tools help students apply theoretical knowledge to practical scenarios, enhancing their problem-solving skills.
Here are some interactive activities to consider:
-
Multiple Choice Questions:
- What is the area of a rectangle with a length of 8 units and a width of 5 units?
- Which shape has a greater perimeter: a square with a side length of 6 units or a rectangle with lengths of 7 units and 3 units?
- If the radius of a circle is 4 units, what is its area?
-
Fill-in-the-Blank Questions:
- The perimeter of a square with a side length of 9 units is __________ units.
- The area of a triangle with a base of 10 units and a height of 5 units is __________ square units.
- The circumference of a circle with a diameter of 12 units is __________ units.
-
True or False Questions:
- A rectangle with a length of 10 units and a width of 4 units has a perimeter of 28 units. (True/False)
- The area of a circle is calculated using the formula \( \pi r^2 \). (True/False)
- A triangle's area can be found using the formula \( \frac{1}{2} \times \text{base} \times \text{height} \). (True/False)
For more comprehensive practice, students can explore these formats:
-
Interactive Online Quizzes:
Websites like ThatQuiz and Quizgecko offer a range of questions on area and perimeter, including multiple-choice, fill-in-the-blank, and true/false questions. These quizzes often provide instant feedback, helping students learn from their mistakes and understand the concepts better.
-
Step-by-Step Solutions:
Detailed solutions to each problem can help students understand the steps involved in solving for area and perimeter. This can include breaking down the problem, applying formulas correctly, and checking the work for accuracy.
-
Customizable Practice Problems:
Teachers and students can create their own practice problems tailored to specific learning goals. This can be done through educational platforms that allow for custom question creation.
Engaging with interactive quizzes and practice problems not only solidifies mathematical understanding but also makes learning fun and engaging. By regularly practicing these types of questions, students can gain confidence and proficiency in calculating area and perimeter.

Multiple Choice Questions
Test your understanding of area and perimeter concepts with these multiple-choice questions:
- What is the formula for calculating the perimeter of a rectangle?
- P = 2(l + w)
- P = lw
- P = l^2 + w^2
- P = 2l + 2w
- What is the formula for calculating the area of a circle?
- A = πr
- A = πr^2
- A = 2πr
- A = π^2r
- Which of the following shapes has both area and perimeter?
- Line segment
- Point
- Circle
- Plane
- What is the formula for calculating the area of a triangle?
- A = bh
- A = 1/2bh
- A = b^2 + h^2
- A = 2bh
- Which of the following shapes has the largest perimeter?
- Rectangle with dimensions 3x5
- Circle with radius 2
- Square with side length 4
- Triangle with side lengths 6, 8, 10
Fill-in-the-Blank Questions
Test your knowledge with these fill-in-the-blank questions:
- The ________ of a rectangle is the distance around it.
- The formula for calculating the area of a rectangle is ________.
- The ________ of a circle is the distance around its outer edge.
- The formula for calculating the area of a circle is ________.
- A ________ is a closed shape with straight sides.
True or False Questions
Test your understanding with these true or false questions:
- The area of a rectangle is calculated by multiplying its length by its width.
- A square has four equal sides and four right angles.
- The perimeter of a circle is equal to twice its radius.
- The area of a triangle can be calculated using the formula A = 1/2 * base * height.
- The perimeter of a polygon is the sum of the lengths of all its sides.
Step-by-Step Solutions and Explanations
Understanding how to solve area and perimeter problems involves breaking down each step and applying the appropriate formulas. Below are detailed solutions and explanations for various types of shapes:
Rectangles and Squares
Example Problem: Find the area and perimeter of a rectangle with a length of 8 cm and a width of 5 cm.
- Identify the formulas:
- Area of a rectangle: \( A = \text{length} \times \text{width} \)
- Perimeter of a rectangle: \( P = 2 \times (\text{length} + \text{width}) \)
- Plug in the values:
- Area: \( A = 8 \, \text{cm} \times 5 \, \text{cm} = 40 \, \text{cm}^2 \)
- Perimeter: \( P = 2 \times (8 \, \text{cm} + 5 \, \text{cm}) = 2 \times 13 \, \text{cm} = 26 \, \text{cm} \)
- Conclusion:
The area of the rectangle is 40 square centimeters, and the perimeter is 26 centimeters.
Triangles
Example Problem: Find the area and perimeter of a right triangle with legs of 3 cm and 4 cm.
- Identify the formulas:
- Area of a triangle: \( A = \frac{1}{2} \times \text{base} \times \text{height} \)
- Perimeter of a right triangle: \( P = \text{base} + \text{height} + \text{hypotenuse} \)
- Hypotenuse: \( \text{hypotenuse} = \sqrt{\text{base}^2 + \text{height}^2} \)
- Calculate the hypotenuse:
- \( \text{hypotenuse} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, \text{cm} \)
- Calculate the area and perimeter:
- Area: \( A = \frac{1}{2} \times 3 \, \text{cm} \times 4 \, \text{cm} = \frac{1}{2} \times 12 \, \text{cm}^2 = 6 \, \text{cm}^2 \)
- Perimeter: \( P = 3 \, \text{cm} + 4 \, \text{cm} + 5 \, \text{cm} = 12 \, \text{cm} \)
- Conclusion:
The area of the right triangle is 6 square centimeters, and the perimeter is 12 centimeters.
Circles
Example Problem: Find the area and circumference of a circle with a radius of 7 cm.
- Identify the formulas:
- Area of a circle: \( A = \pi r^2 \)
- Circumference of a circle: \( C = 2\pi r \)
- Plug in the values:
- Area: \( A = \pi \times 7^2 = \pi \times 49 = 153.94 \, \text{cm}^2 \) (using \( \pi \approx 3.14 \))
- Circumference: \( C = 2\pi \times 7 = 2 \times 3.14 \times 7 = 43.96 \, \text{cm} \)
- Conclusion:
The area of the circle is approximately 153.94 square centimeters, and the circumference is approximately 43.96 centimeters.
Polygons
Example Problem: Find the area of a regular hexagon with a side length of 6 cm.
- Identify the formula:
- Area of a regular hexagon: \( A = \frac{3\sqrt{3}}{2} s^2 \)
- Plug in the values:
- Area: \( A = \frac{3\sqrt{3}}{2} \times 6^2 = \frac{3\sqrt{3}}{2} \times 36 = 93.53 \, \text{cm}^2 \) (using \( \sqrt{3} \approx 1.732 \))
- Conclusion:
The area of the regular hexagon is approximately 93.53 square centimeters.
Complex Shapes
Example Problem: Find the area of a composite shape consisting of a rectangle with a length of 10 cm and width of 4 cm, and a semicircle with a diameter of 4 cm attached to one of the shorter sides.
- Calculate the area of the rectangle:
- Area of the rectangle: \( A_{\text{rectangle}} = \text{length} \times \text{width} = 10 \, \text{cm} \times 4 \, \text{cm} = 40 \, \text{cm}^2 \)
- Calculate the area of the semicircle:
- Radius of the semicircle: \( r = \frac{\text{diameter}}{2} = \frac{4 \, \text{cm}}{2} = 2 \, \text{cm} \)
- Area of the semicircle: \( A_{\text{semicircle}} = \frac{1}{2} \pi r^2 = \frac{1}{2} \pi (2 \, \text{cm})^2 = \frac{1}{2} \pi \times 4 = 6.28 \, \text{cm}^2 \) (using \( \pi \approx 3.14 \))
- Calculate the total area:
- Total area: \( A_{\text{total}} = A_{\text{rectangle}} + A_{\text{semicircle}} = 40 \, \text{cm}^2 + 6.28 \, \text{cm}^2 = 46.28 \, \text{cm}^2 \)
- Conclusion:
The area of the composite shape is approximately 46.28 square centimeters.
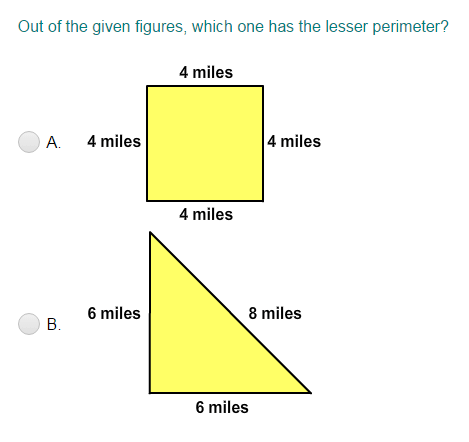
Tips and Tricks for Solving Area and Perimeter Problems
Understanding the concepts of area and perimeter is crucial in solving geometry problems efficiently. Here are some tips and tricks to help you tackle these problems with ease:
- Memorize Key Formulas:
- Rectangle:
- Perimeter: \( P = 2l + 2w \)
- Area: \( A = l \times w \)
- Square:
- Perimeter: \( P = 4s \)
- Area: \( A = s^2 \)
- Triangle:
- Perimeter: \( P = a + b + c \)
- Area: \( A = \frac{1}{2} b \times h \)
- Circle:
- Circumference: \( C = 2\pi r \)
- Area: \( A = \pi r^2 \)
- Rectangle:
- Understand Relationships: Recognize how changing dimensions affect area and perimeter. For example, doubling the side of a square quadruples the area but only doubles the perimeter.
- Break Down Complex Shapes: Divide complex shapes into simpler ones whose area and perimeter can be calculated easily, then sum up the results. For instance, a composite shape might be split into rectangles and triangles.
- Use Visual Aids: Draw diagrams to visualize the problem. Label all known dimensions and denote unknowns with variables. This helps in setting up equations correctly.
- Check Units: Ensure consistency in measurement units. Convert all measurements to the same unit before performing calculations.
- Practice Word Problems: Apply formulas in real-world scenarios to enhance understanding. For example, calculating the perimeter of a garden to estimate the length of the fencing required.
- Double-Check Calculations: Verify your calculations by redoing them or using a different method to ensure accuracy.
- Understand Special Properties: Learn properties of specific shapes like the fact that a square has the maximum area for a given perimeter, or a circle has the minimum perimeter for a given area.
By keeping these tips in mind, you can approach area and perimeter problems more strategically and with greater confidence.
Common Mistakes to Avoid
Understanding common mistakes can help you avoid them and improve your accuracy when solving area and perimeter problems. Here are some of the most frequent errors and tips to avoid them:
-
Confusing Area with Perimeter:
Area measures the space inside a shape, while perimeter measures the distance around a shape. Ensure you are using the correct formula for the problem at hand:
- For rectangles, area is calculated as \( \text{length} \times \text{width} \) and perimeter as \( 2(\text{length} + \text{width}) \).
- For circles, area is \( \pi r^2 \) and perimeter (circumference) is \( 2\pi r \).
-
Incorrect Unit Conversion:
Always convert units to the same system before performing calculations. For example, if one measurement is in meters and another in centimeters, convert them to the same unit.
-
Misidentifying Shape Dimensions:
Ensure you correctly identify the dimensions of a shape. For instance, in a triangle, the base and height must be perpendicular.
-
Incorrect Formula Application:
Use the right formula for the specific shape you are working with. For instance:
- Triangles: \( \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \).
- Parallelograms: \( \text{Area} = \text{base} \times \text{height} \).
-
Omitting Units:
Always include units in your final answer to avoid confusion and ensure clarity.
-
Misinterpreting Composite Shapes:
For complex shapes, break them down into simpler shapes, calculate the area or perimeter of each, and then combine the results appropriately.
By being mindful of these common mistakes and following the correct steps, you can improve your accuracy and confidence in solving area and perimeter problems.
Xem video 'Câu Đố Toán Học - Chu Vi (Phần 1)' để học và kiểm tra kiến thức về chu vi trong toán học.
Câu Đố Toán Học - Chu Vi (Phần 1)
READ MORE:
Video về các trò chơi toán học giúp bạn nhanh chóng suy nghĩ và tính toán chu vi và diện tích. Tham gia ngay để rèn luyện kỹ năng toán học của bạn!
TRÒ CHƠI TOÁN HỌC | SUY NGHĨ NHANH | Chu Vi và Diện Tích