Topic find perimeter and area of triangle: Discover how to find the perimeter and area of a triangle with easy steps and practical formulas. This guide will help you understand and apply different methods for various types of triangles, enhancing your geometry skills and making calculations straightforward and fun.
Table of Content
- Perimeter and Area of a Triangle
- Introduction to Triangles
- Basic Triangle Properties
- Understanding the Perimeter of a Triangle
- Calculating Perimeter of Different Types of Triangles
- Equilateral Triangle Perimeter
- Isosceles Triangle Perimeter
- Scalene Triangle Perimeter
- Understanding the Area of a Triangle
- Calculating Area Using Base and Height
- Area of Right-Angled Triangle
- Area of Equilateral Triangle
- Area of Isosceles Triangle
- Using Heron's Formula for Area
- Calculating Area with Two Sides and Included Angle
- Real-life Applications of Perimeter and Area
- Practical Examples and Problems
- Fun Facts About Triangles
- Frequently Asked Questions
- YOUTUBE: Hướng dẫn cách tìm diện tích và chu vi của tam giác với Thầy J. Video này cung cấp các bước chi tiết và dễ hiểu để bạn nắm vững kiến thức.
Perimeter and Area of a Triangle
The perimeter and area of a triangle are fundamental concepts in geometry. This guide explains various methods to calculate these properties for different types of triangles.
Perimeter of a Triangle
The perimeter of a triangle is the total distance around the triangle, which is the sum of the lengths of its three sides.
- For any triangle with sides \(a\), \(b\), and \(c\), the perimeter \(P\) is given by: \[ P = a + b + c \]
- For an equilateral triangle (all sides equal): \[ P = 3a \]
- For an isosceles triangle (two sides equal): \[ P = 2a + b \]
Area of a Triangle
The area of a triangle is the total space enclosed within its three sides. The formula to calculate the area varies based on the known parameters.
- When the base (\(b\)) and height (\(h\)) are known: \[ \text{Area} = \frac{1}{2} \times b \times h \]
- For an equilateral triangle with side \(a\): \[ \text{Area} = \frac{\sqrt{3}}{4} \times a^2 \]
- Using Heron's Formula when all three sides (\(a\), \(b\), \(c\)) are known:
- First, calculate the semi-perimeter (\(s\)): \[ s = \frac{a + b + c}{2} \]
- Then, use Heron's Formula: \[ \text{Area} = \sqrt{s \times (s - a) \times (s - b) \times (s - c)} \]
- When two sides and the included angle (\(\gamma\)) are known: \[ \text{Area} = \frac{1}{2} \times a \times b \times \sin(\gamma) \]
Examples
| Triangle Type | Given | Formula | Calculation |
|---|---|---|---|
| Scalene Triangle | a=5, b=6, c=7 | Heron's Formula | \[ s = \frac{5 + 6 + 7}{2} = 9 \\ \text{Area} = \sqrt{9 \times (9-5) \times (9-6) \times (9-7)} = \sqrt{9 \times 4 \times 3 \times 2} = \sqrt{216} \approx 14.7 \] |
| Right Triangle | Base=6, Height=8 | Base-Height Formula | \[ \text{Area} = \frac{1}{2} \times 6 \times 8 = 24 \] |
| Equilateral Triangle | Side=4 | Equilateral Triangle Formula | \[ \text{Area} = \frac{\sqrt{3}}{4} \times 4^2 = 4\sqrt{3} \approx 6.93 \] |
Understanding these formulas allows you to calculate the perimeter and area of any triangle given the appropriate measurements.

READ MORE:
Introduction to Triangles
A triangle is a fundamental geometric shape consisting of three sides and three angles. It is one of the simplest forms of polygons, making it a crucial element in geometry. Triangles are classified into different types based on the length of their sides and the measures of their angles. The study of triangles includes understanding various properties and formulas to calculate their perimeter and area.
There are several types of triangles:
- Equilateral Triangle: All three sides are equal, and all three angles are 60 degrees.
- Isosceles Triangle: Two sides are of equal length, and the angles opposite these sides are equal.
- Scalene Triangle: All three sides and all three angles are different.
- Right Triangle: One of the angles is 90 degrees.
To work with triangles effectively, it is essential to understand how to calculate their perimeter and area:
- Perimeter of a Triangle: The perimeter is the total length around the triangle. For a triangle with sides \(a\), \(b\), and \(c\), the perimeter \(P\) is given by: \[ P = a + b + c \]
- Area of a Triangle: The area represents the space enclosed within the triangle. The most common formula to calculate the area when the base (\(b\)) and height (\(h\)) are known is: \[ \text{Area} = \frac{1}{2} \times b \times h \]
- Heron's Formula: When all three sides of a triangle are known, Heron's formula can be used to find the area. First, calculate the semi-perimeter (\(s\)): \[ s = \frac{a + b + c}{2} \] Then, use Heron's formula: \[ \text{Area} = \sqrt{s(s - a)(s - b)(s - c)} \]
- Area Using Trigonometry: If two sides and the included angle are known, the area can be calculated using trigonometry: \[ \text{Area} = \frac{1}{2} \times a \times b \times \sin(\gamma) \]
Understanding these fundamental concepts and formulas is essential for solving problems related to triangles, whether in academic studies or practical applications.
Basic Triangle Properties
Triangles are fundamental shapes in geometry with unique properties that make them essential in various mathematical applications. Understanding the basic properties of triangles helps in solving problems related to their perimeter and area.
Here are some key properties of triangles:
- Types of Triangles by Sides:
- Equilateral Triangle: All three sides are of equal length, and all angles are 60 degrees each.
- Isosceles Triangle: Two sides are of equal length, and the angles opposite these sides are equal.
- Scalene Triangle: All three sides and all three angles are different.
- Types of Triangles by Angles:
- Right Triangle: One angle is exactly 90 degrees.
- Acute Triangle: All three angles are less than 90 degrees.
- Obtuse Triangle: One angle is greater than 90 degrees.
Basic formulas used in triangle geometry include:
- Perimeter of a Triangle: The perimeter is the total length around the triangle. It is calculated by adding the lengths of all three sides. \[ P = a + b + c \]
- Area of a Triangle: The area can be found using different formulas based on the available information:
- When the base (\(b\)) and height (\(h\)) are known: \[ \text{Area} = \frac{1}{2} \times b \times h \]
- Using Heron's Formula when all three sides are known:
- Calculate the semi-perimeter (\(s\)): \[ s = \frac{a + b + c}{2} \]
- Then use Heron's Formula: \[ \text{Area} = \sqrt{s(s - a)(s - b)(s - c)} \]
- Using trigonometry when two sides and the included angle (\(\gamma\)) are known: \[ \text{Area} = \frac{1}{2} \times a \times b \times \sin(\gamma) \]
These properties and formulas form the basis of understanding and solving various geometric problems involving triangles, making them essential knowledge for students and professionals alike.
Understanding the Perimeter of a Triangle
The perimeter of a triangle is the total distance around the triangle, which is calculated by adding the lengths of its three sides. This fundamental concept is essential for various geometric calculations and practical applications.
To find the perimeter of a triangle, you simply sum the lengths of its sides. Here is the basic formula:
- For any triangle with sides \( a \), \( b \), and \( c \), the perimeter \( P \) is given by: \[ P = a + b + c \]
Calculating the Perimeter for Different Types of Triangles
Depending on the type of triangle, the method to find the perimeter remains straightforward. Here are specific cases:
- Equilateral Triangle: All sides are equal. \[ P = 3 \times s \] where \( s \) is the length of a side.
- Isosceles Triangle: Two sides are of equal length. \[ P = 2 \times l + b \] where \( l \) is the length of the equal sides, and \( b \) is the base.
- Scalene Triangle: All sides are of different lengths. \[ P = a + b + c \]
- Right Triangle: One angle is 90 degrees. You can use the Pythagorean Theorem if you know two sides: \[ P = a + b + \sqrt{a^2 + b^2} \] where \( a \) and \( b \) are the legs of the triangle, and \( c \) is the hypotenuse.
Example Problems
| Type of Triangle | Given | Perimeter Calculation |
|---|---|---|
| Scalene Triangle | Sides: 5 cm, 7 cm, 8 cm | \[ P = 5 + 7 + 8 = 20 \, \text{cm} \] |
| Equilateral Triangle | Side: 6 cm | \[ P = 3 \times 6 = 18 \, \text{cm} \] |
| Isosceles Triangle | Sides: 5 cm, 5 cm, 6 cm | \[ P = 2 \times 5 + 6 = 16 \, \text{cm} \] |
| Right Triangle | Legs: 3 cm, 4 cm | \[ P = 3 + 4 + \sqrt{3^2 + 4^2} = 3 + 4 + 5 = 12 \, \text{cm} \] |
By understanding and applying these formulas, you can easily calculate the perimeter of any triangle, enhancing your problem-solving skills in geometry.
Calculating Perimeter of Different Types of Triangles
The perimeter of a triangle is the total length around the triangle, calculated by summing the lengths of its three sides. Different types of triangles have specific properties that simplify the calculation of their perimeters.
Equilateral Triangle
An equilateral triangle has all three sides of equal length. The formula for calculating the perimeter of an equilateral triangle is straightforward:
- If each side of the triangle is \( s \): \[ P = 3s \]
Isosceles Triangle
An isosceles triangle has two sides of equal length. The formula for calculating the perimeter of an isosceles triangle is:
- If the equal sides are \( l \) and the base is \( b \): \[ P = 2l + b \]
Scalene Triangle
A scalene triangle has all sides of different lengths. The perimeter is calculated by simply adding the lengths of all three sides:
- If the sides are \( a \), \( b \), and \( c \): \[ P = a + b + c \]
Right Triangle
A right triangle has one 90-degree angle. To find the perimeter when the lengths of the two legs (\( a \) and \( b \)) are known, use the Pythagorean theorem to find the hypotenuse (\( c \)) and then sum all three sides:
- If the legs are \( a \) and \( b \): \[ c = \sqrt{a^2 + b^2} \] Then, \[ P = a + b + c \]
Examples
| Type of Triangle | Given | Perimeter Calculation |
|---|---|---|
| Equilateral Triangle | Side: 6 cm | \[ P = 3 \times 6 = 18 \, \text{cm} \] |
| Isosceles Triangle | Sides: 5 cm, 5 cm, 8 cm | \[ P = 2 \times 5 + 8 = 18 \, \text{cm} \] |
| Scalene Triangle | Sides: 3 cm, 4 cm, 5 cm | \[ P = 3 + 4 + 5 = 12 \, \text{cm} \] |
| Right Triangle | Legs: 3 cm, 4 cm | \[ c = \sqrt{3^2 + 4^2} = 5 \, \text{cm} \\ P = 3 + 4 + 5 = 12 \, \text{cm} \] |
By understanding and applying these formulas, you can calculate the perimeter of any triangle type, aiding in various mathematical and practical applications.
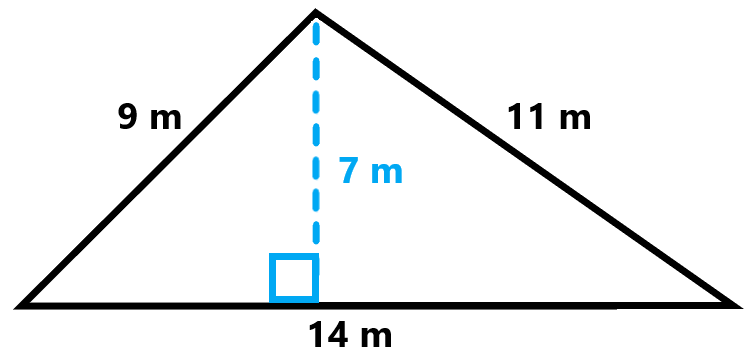
Equilateral Triangle Perimeter
An equilateral triangle is a special type of triangle where all three sides are of equal length and each angle is 60 degrees. Calculating the perimeter of an equilateral triangle is straightforward because of its symmetry.
To find the perimeter of an equilateral triangle, use the following formula:
- If each side of the triangle is \( s \): \[ P = 3s \]
Steps to Calculate the Perimeter of an Equilateral Triangle
- Measure the length of one side of the equilateral triangle.
- Multiply this length by 3 to find the perimeter.
For example, if each side of an equilateral triangle is 5 cm, the perimeter calculation would be:
- \[ P = 3 \times 5 = 15 \, \text{cm} \]
Practical Applications
Understanding the perimeter of an equilateral triangle is useful in various practical scenarios, such as:
- Determining the amount of material needed to frame a triangular artwork.
- Calculating the fencing required to enclose a triangular garden.
- Designing equilateral triangular shapes in architecture and engineering.
Example Problems
| Side Length | Perimeter Calculation | Perimeter |
|---|---|---|
| 4 cm | \[ P = 3 \times 4 = 12 \, \text{cm} \] | 12 cm |
| 7.5 cm | \[ P = 3 \times 7.5 = 22.5 \, \text{cm} \] | 22.5 cm |
| 10 cm | \[ P = 3 \times 10 = 30 \, \text{cm} \] | 30 cm |
By following these steps and understanding the formula, you can easily calculate the perimeter of any equilateral triangle, enhancing your geometry skills and solving real-world problems efficiently.
Isosceles Triangle Perimeter
An isosceles triangle is a type of triangle that has two sides of equal length and one side that is different. Calculating the perimeter of an isosceles triangle involves summing the lengths of all three sides.
The formula for calculating the perimeter of an isosceles triangle is:
- If the lengths of the equal sides are \( l \) and the base is \( b \): \[ P = 2l + b \]
Steps to Calculate the Perimeter of an Isosceles Triangle
- Measure the length of the two equal sides (\( l \)).
- Measure the length of the base (\( b \)).
- Substitute these values into the formula and add them together.
For example, if the equal sides of an isosceles triangle are 5 cm each and the base is 8 cm, the perimeter calculation would be:
- \[ P = 2 \times 5 + 8 = 10 + 8 = 18 \, \text{cm} \]
Practical Applications
Understanding the perimeter of an isosceles triangle is useful in various practical scenarios, such as:
- Determining the amount of material needed to create a frame for an isosceles triangular artwork.
- Calculating the perimeter for landscaping projects involving triangular sections.
- Designing and planning for construction projects that incorporate isosceles triangular shapes.
Example Problems
| Equal Sides (l) | Base (b) | Perimeter Calculation | Perimeter |
|---|---|---|---|
| 6 cm | 10 cm | \[ P = 2 \times 6 + 10 = 12 + 10 = 22 \, \text{cm} \] | 22 cm |
| 7.5 cm | 12 cm | \[ P = 2 \times 7.5 + 12 = 15 + 12 = 27 \, \text{cm} \] | 27 cm |
| 8 cm | 14 cm | \[ P = 2 \times 8 + 14 = 16 + 14 = 30 \, \text{cm} \] | 30 cm |
By following these steps and understanding the formula, you can easily calculate the perimeter of any isosceles triangle, enhancing your geometry skills and solving real-world problems efficiently.
Scalene Triangle Perimeter
A scalene triangle is a type of triangle where all three sides have different lengths, and all three angles are different. To find the perimeter of a scalene triangle, you simply add up the lengths of its three sides.
The formula to calculate the perimeter (P) of a scalene triangle is:
\( P = a + b + c \)
where:
- \( a \) is the length of the first side
- \( b \) is the length of the second side
- \( c \) is the length of the third side
Let's look at an example to understand this better:
Example 1: Find the perimeter of a scalene triangle with sides of lengths 5 cm, 7 cm, and 9 cm.
Solution:
- Identify the lengths of the sides: \( a = 5 \) cm, \( b = 7 \) cm, \( c = 9 \) cm.
- Apply the formula: \( P = a + b + c \).
- Substitute the values: \( P = 5 + 7 + 9 \).
- Calculate the sum: \( P = 21 \) cm.
Therefore, the perimeter of the given scalene triangle is 21 cm.
Example 2: If the perimeter of a scalene triangle is 30 inches and two sides are 10 inches and 12 inches, find the length of the third side.
Solution:
- Let the sides be \( a = 10 \) inches, \( b = 12 \) inches, and \( c \) be the unknown side.
- Given the perimeter \( P = 30 \) inches, use the formula \( P = a + b + c \).
- Rearrange the formula to solve for \( c \): \( c = P - a - b \).
- Substitute the known values: \( c = 30 - 10 - 12 \).
- Calculate the result: \( c = 8 \) inches.
Therefore, the length of the third side is 8 inches.
In cases where you know two sides of the triangle and the angle between them, you can use the Law of Cosines to find the third side before calculating the perimeter.
The Law of Cosines formula is:
\( c^2 = a^2 + b^2 - 2ab \cos(C) \)
where \( C \) is the angle between sides \( a \) and \( b \). Once you have the length of the third side, you can use the perimeter formula to find the total perimeter of the scalene triangle.
Understanding the Area of a Triangle
The area of a triangle is the measure of the space enclosed within its three sides. There are several methods to calculate the area of a triangle depending on the given information. Here, we will explore various formulas and methods to understand the concept in detail.
1. Using Base and Height
The most common way to find the area of a triangle is by using its base and height. The formula is:
\[ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} \]
For example, if the base \( b \) is 10 units and the height \( h \) is 5 units, the area \( A \) is calculated as:
\[ A = \frac{1}{2} \times 10 \times 5 = 25 \text{ square units} \]
2. Using Heron's Formula
When the lengths of all three sides of a triangle are known, Heron's formula can be used. First, calculate the semi-perimeter \( s \):
\[ s = \frac{a + b + c}{2} \]
Then, use the semi-perimeter to find the area:
\[ \text{Area} = \sqrt{s(s - a)(s - b)(s - c)} \]
For instance, if the sides are \( a = 5 \), \( b = 6 \), and \( c = 7 \), the semi-perimeter \( s \) is:
\[ s = \frac{5 + 6 + 7}{2} = 9 \]
The area \( A \) is:
\[ A = \sqrt{9(9 - 5)(9 - 6)(9 - 7)} = \sqrt{9 \times 4 \times 3 \times 2} = \sqrt{216} = 14.7 \text{ square units} \]
3. Using Trigonometric Functions
When two sides and the included angle are known, the area can be calculated using trigonometric functions:
\[ \text{Area} = \frac{1}{2} \times a \times b \times \sin(\theta) \]
For example, with sides \( a = 8 \) units, \( b = 6 \) units, and the included angle \( \theta = 30^\circ \), the area \( A \) is:
\[ A = \frac{1}{2} \times 8 \times 6 \times \sin(30^\circ) = \frac{1}{2} \times 8 \times 6 \times 0.5 = 12 \text{ square units} \]
4. Area of Specific Types of Triangles
- Right-Angled Triangle: For a right-angled triangle, the area is given by:
\[ \text{Area} = \frac{1}{2} \times \text{Base} \times \text{Height} \] - Equilateral Triangle: For an equilateral triangle where all sides are equal, the area is:
\[ \text{Area} = \frac{\sqrt{3}}{4} \times \text{side}^2 \] - Isosceles Triangle: For an isosceles triangle with equal sides \( a \) and base \( b \), the area is:
\[ \text{Area} = \frac{1}{4} b \sqrt{4a^2 - b^2} \]
Understanding and using these formulas will help you calculate the area of any triangle, whether you have the base and height, the lengths of all sides, or specific angles and sides.

Calculating Area Using Base and Height
The area of a triangle can be easily calculated if you know the base and height of the triangle. This method is applicable to all types of triangles: scalene, isosceles, and equilateral.
The formula to find the area of a triangle is given by:
where b is the base of the triangle and h is the height.
Step-by-Step Calculation
-
Identify the base and height of the triangle. The base can be any one of the sides, and the height is the perpendicular distance from the base to the opposite vertex.
-
Measure the length of the base (b) and the height (h) in the same units.
-
Plug the values into the formula:
-
Perform the multiplication and then divide by 2 to find the area.
For example, if the base of the triangle is 8 cm and the height is 5 cm, the area would be calculated as follows:
Thus, the area of the triangle is 20 square centimeters.
Understanding how to calculate the area using base and height is fundamental and can be applied to various types of triangles in both theoretical problems and real-life applications.
Area of Right-Angled Triangle
The area of a right-angled triangle can be calculated using a simple and well-known formula. Since one of the angles is 90 degrees, the two sides that form the right angle are the base and the height. The formula to find the area is:
Where b is the length of the base and h is the height of the triangle. Follow these steps to calculate the area:
- Identify the base and height of the triangle. These are the two sides that form the right angle.
- Use the formula to calculate the area.
- Substitute the values of the base and height into the formula.
- Perform the multiplication and division to find the area.
Here are a few examples to illustrate:
- Example 1: If the base b is 6 inches and the height h is 8 inches:
- Example 2: If the height h is 12 cm and the base b is 5 cm:
- Example 3: If the height h is 2 m and the base b is 6 m:
Remember, the key steps are to correctly identify the base and height and then apply the formula accurately to find the area of the right-angled triangle.
Area of Equilateral Triangle
An equilateral triangle is a special type of triangle where all three sides are of equal length, and all three internal angles are equal, each measuring 60 degrees. The formula to find the area of an equilateral triangle is derived using trigonometric identities and properties of the triangle.
The formula to calculate the area of an equilateral triangle is:
\[ \text{Area} = \frac{\sqrt{3}}{4} a^2 \]
where \( a \) is the length of a side of the triangle.
Steps to Calculate the Area
Measure the length of one side of the equilateral triangle.
Substitute the length of the side into the formula:
\[ \text{Area} = \frac{\sqrt{3}}{4} a^2 \]For example, if the side length \( a \) is 6 units:
\[ \text{Area} = \frac{\sqrt{3}}{4} \times 6^2 = \frac{\sqrt{3}}{4} \times 36 = 9\sqrt{3} \, \text{square units} \]Express the result with the appropriate units.
Example Calculations
For an equilateral triangle with a side length of 4 cm:
\[ \text{Area} = \frac{\sqrt{3}}{4} \times 4^2 = \frac{\sqrt{3}}{4} \times 16 = 4\sqrt{3} \, \text{cm}^2 \]For an equilateral triangle with a side length of 8 in:
\[ \text{Area} = \frac{\sqrt{3}}{4} \times 8^2 = \frac{\sqrt{3}}{4} \times 64 = 16\sqrt{3} \, \text{in}^2 \]For an equilateral triangle with a side length of 10 units:
\[ \text{Area} = \frac{\sqrt{3}}{4} \times 10^2 = \frac{\sqrt{3}}{4} \times 100 = 25\sqrt{3} \, \text{square units} \]
Properties of Equilateral Triangle
- All sides are equal in length.
- All internal angles are equal to 60 degrees.
- It is a regular polygon with 3 sides.
- The area is given by the formula \( \frac{\sqrt{3}}{4} a^2 \).
- The perimeter is \( 3a \).
Area of Isosceles Triangle
An isosceles triangle is a triangle with at least two sides of equal length. To find the area of an isosceles triangle, you can use the following formula:
\[Area = \frac{1}{2} \times base \times height\]
Where:
- The base is the unequal side of the triangle.
- The height is the perpendicular distance from the base to the opposite vertex.
If the lengths of the two equal sides are given (a) and the length of the base is given (b), you can find the height (h) using the Pythagorean theorem:
\(h = \sqrt{a^2 - \frac{b^2}{4}}\)
Once you have the height, you can use the area formula mentioned earlier to find the area of the isosceles triangle.
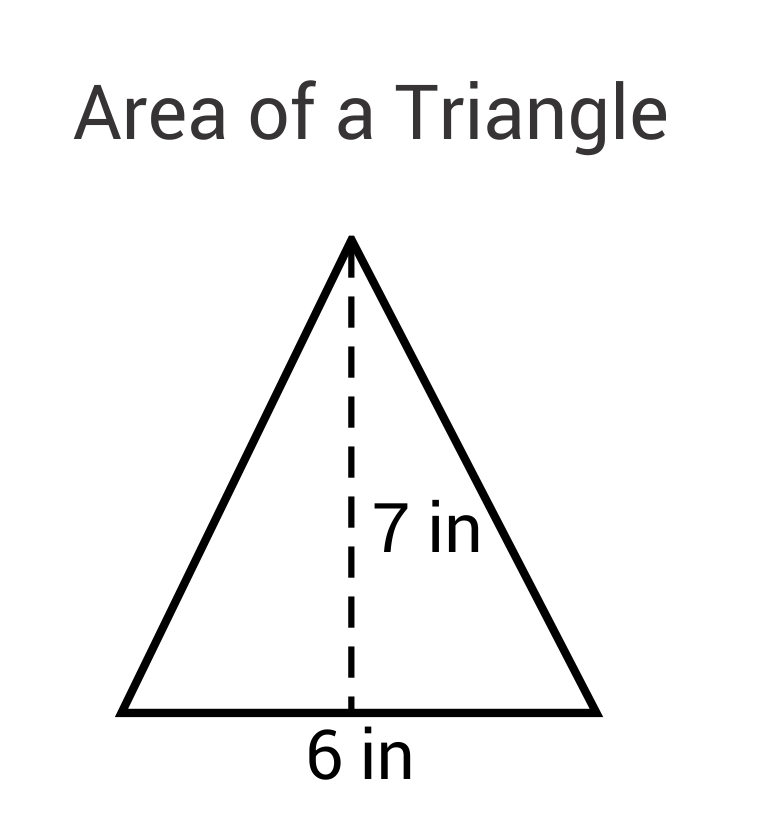
Using Heron's Formula for Area
Heron's formula is a method for finding the area of a triangle when the lengths of all three sides are known. The formula is as follows:
\[Area = \sqrt{s(s - a)(s - b)(s - c)}\]
Where:
- a, b, and c are the lengths of the three sides of the triangle.
- s is the semi-perimeter of the triangle, calculated as \(s = \frac{a + b + c}{2}\).
To use Heron's formula:
- Calculate the semi-perimeter of the triangle using the formula \(s = \frac{a + b + c}{2}\).
- Substitute the values of the side lengths and the semi-perimeter into Heron's formula.
- Calculate the square root of the result to find the area of the triangle.
This formula is particularly useful when you know the lengths of all three sides of a triangle but do not have information about its height or angles.
Calculating Area with Two Sides and Included Angle
When you know the lengths of two sides of a triangle and the measure of the included angle between them, you can use the following formula to find the area:
\[Area = \frac{1}{2} \times a \times b \times \sin(C)\]
Where:
- a and b are the lengths of the two sides.
- C is the measure of the included angle between the two sides, in radians.
To use this formula:
- Convert the angle measure from degrees to radians if necessary, as most trigonometric functions expect angle measures in radians.
- Multiply the lengths of the two sides by the sine of the included angle.
- Divide the result by 2 to find the area of the triangle.
This formula is derived from the trigonometric definition of the area of a triangle and is particularly useful when you know the lengths of two sides and the angle between them.
Real-life Applications of Perimeter and Area
The concepts of perimeter and area are fundamental in various real-life scenarios. Here are some practical applications:
- Construction: Builders and architects use perimeter and area calculations extensively in construction projects. They determine the amount of material needed for fencing, flooring, roofing, and landscaping.
- Land Surveying: Surveyors use perimeter measurements to demarcate property boundaries, while area calculations help assess land value and plan urban development.
- Packaging: Manufacturers consider the perimeter and area of packaging materials to optimize space utilization, reduce waste, and ensure efficient transportation and storage.
- Geometry: Perimeter and area concepts are essential in geometry, enabling the calculation of dimensions for shapes like rectangles, circles, and irregular polygons.
- Agriculture: Farmers use perimeter measurements to fence fields and calculate the area of land for cultivation. This information aids in crop planning, irrigation, and yield estimation.
- Art and Design: Artists and designers use perimeter and area concepts to create aesthetically pleasing compositions, plan layouts, and determine material requirements for projects.
- Finance: Real estate agents use area calculations to determine property values, while businesses analyze floor area to optimize retail space and rental income.
These are just a few examples of how understanding perimeter and area is crucial in various aspects of daily life and professional fields.
Practical Examples and Problems
Let's explore some practical examples and problems involving the perimeter and area of triangles:
- Example 1: Fence Installation
You want to install a fence around your rectangular garden, which measures 10 meters by 15 meters. What is the perimeter of the garden, and how much fencing material do you need?
- Example 2: Tile Flooring
You are planning to tile the floor of a triangular-shaped kitchen. The lengths of the two shorter sides are 6 feet and 8 feet, and the included angle is 60 degrees. How many square feet of tiles do you need?
- Problem 1: Garden Bed Area
An equilateral triangular garden bed has a side length of 5 meters. Calculate the area of the garden bed.
- Problem 2: Paint Coverage
You are painting the walls of a triangular room. The lengths of the walls are 4 meters, 5 meters, and 7 meters. How much paint is needed if one liter covers 10 square meters?
- Problem 3: Roofing Material
A triangular roof has a base of 12 meters and a height of 9 meters. Calculate the area of the roof to determine the amount of roofing material required.
Solving these examples and problems will help reinforce your understanding of how to apply perimeter and area concepts in real-life situations.

Fun Facts About Triangles
Triangles are fascinating geometric shapes that have intrigued mathematicians, scientists, and artists for centuries. Here are some fun and interesting facts about triangles:
- Triangles are the simplest polygon, consisting of three sides and three angles.
- The sum of the interior angles of a triangle is always 180 degrees.
- There are various types of triangles, including equilateral, isosceles, scalene, right-angled, and obtuse-angled triangles.
- Equilateral triangles have all three sides of equal length and all three angles equal to 60 degrees.
- An isosceles triangle has two sides of equal length and two equal angles.
- Scalene triangles have all sides of different lengths and no equal angles.
- The area of a triangle can be calculated using different formulas, such as base times height divided by 2 or Heron's formula.
- Triangles have a variety of real-life applications, including architecture, engineering, and art.
- The Pythagorean theorem, which states that in a right-angled triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides, is fundamental in triangle geometry.
- Triangles are used in navigation and mapmaking to calculate distances and angles.
- The study of triangles and their properties is a fundamental aspect of geometry, laying the groundwork for more complex mathematical concepts.
Frequently Asked Questions
Here are some common questions and answers about finding the perimeter and area of triangles:
- What is the perimeter of a triangle?
The perimeter of a triangle is the total length of all its sides combined. - How do you calculate the perimeter of a triangle?
To find the perimeter of a triangle, add the lengths of all three sides together. - What is the area of a triangle?
The area of a triangle is the space enclosed within its three sides. - How is the area of a triangle calculated?
The area of a triangle can be calculated using various formulas, such as base times height divided by 2 or Heron's formula. - What is Heron's formula?
Heron's formula is a method for calculating the area of a triangle when you know the lengths of all three sides. It is expressed as the square root of s times (s-a) times (s-b) times (s-c), where s is the semi-perimeter of the triangle, and a, b, and c are the lengths of its sides. - Can you find the area of a triangle if you only know the lengths of two sides and the included angle?
Yes, you can use the formula: Area = 1/2 * (side1) * (side2) * sin(angle). - What are some real-life applications of finding the perimeter and area of triangles?
Triangles are used in various fields such as architecture, engineering, physics, and geometry. They are used to calculate distances, angles, areas, and volumes in real-world scenarios. - Why are triangles important in geometry?
Triangles are fundamental geometric shapes that serve as the building blocks for many other geometric concepts. Understanding triangles and their properties is crucial for solving more complex mathematical problems.
Hướng dẫn cách tìm diện tích và chu vi của tam giác với Thầy J. Video này cung cấp các bước chi tiết và dễ hiểu để bạn nắm vững kiến thức.
Cách Tìm Diện Tích và Chu Vi của Tam Giác | Toán với Thầy J
READ MORE:
Video này hướng dẫn cách tìm diện tích và chu vi của tam giác một cách chi tiết và dễ hiểu, giúp bạn nắm vững kiến thức toán học.
Cách Tìm Diện Tích và Chu Vi của Tam Giác