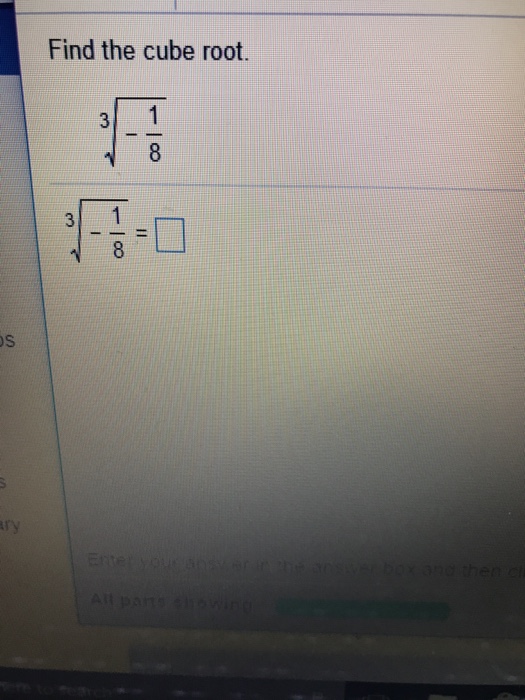
Topic what is a negative square root: Understanding the concept of a negative square root is crucial in mathematics. A negative square root refers to the square root of a negative number, which does not exist within the set of real numbers. Instead, it introduces the realm of imaginary numbers, represented by the unit 'i'. This article will delve into the intricacies of negative square roots and their applications.
Table of Content
- Understanding Negative Square Roots
- Introduction
- Understanding Square Roots
- Square Roots of Negative Numbers
- Properties of Square Roots
- Examples
- Definition of Negative Square Roots
- Imaginary Numbers
- Calculating Negative Square Roots
- Examples and Applications
- Real-World Uses of Imaginary Numbers
- Common Misconceptions
- Graphing Square Root Functions
- Conclusion
- YOUTUBE: Hướng dẫn chi tiết cách tìm căn bậc hai của số âm bằng cách sử dụng đơn vị ảo i. Xem ngay video để hiểu rõ hơn.
Understanding Negative Square Roots
A square root of a number \(x\) is a number \(r\) such that \(r^2 = x\). For positive numbers, there are two square roots: one positive and one negative. For example, both \(5\) and \(-5\) are square roots of \(25\) because \(5^2 = 25\) and \((-5)^2 = 25\).
Principal Square Root
The principal square root of a number is the non-negative root. For instance:
- \(\sqrt{25} = 5\)
The negative square root is denoted as:
- \(-\sqrt{25} = -5\)
Square Roots of Negative Numbers
The square root of a negative number is not a real number but an imaginary number. This involves the imaginary unit \(i\), where \(i = \sqrt{-1}\). For example:
- \(\sqrt{-4} = 2i\)
- \(\sqrt{-9} = 3i\)
Examples and Properties
| Expression | Result |
| \(\sqrt{36}\) | 6 |
| \(-\sqrt{81}\) | -9 |
| \(\sqrt{-16}\) | 4i |
| \(\sqrt{-25}\) | 5i |
Solving Equations Involving Square Roots
When solving equations like \(x^2 = a\), where \(a\) is positive, the solutions are:
- \(x = \pm \sqrt{a}\)
For \(a\) negative, the solutions involve imaginary numbers:
- \(x = \pm i \sqrt{|a|}\)
Complex Numbers and Square Roots
In complex numbers, we use the formula:
\(\sqrt{-p} = i\sqrt{p}\), where \(p\) is a positive real number.
For example:
- \(\sqrt{-9} = i\sqrt{9} = 3i\)
- \(\sqrt{-16} = i\sqrt{16} = 4i\)

READ MORE:
Introduction
Understanding the concept of a negative square root is fundamental in both real and complex number systems. In real numbers, the square root of a negative number does not exist, as no real number squared equals a negative number. However, in the realm of complex numbers, we introduce the imaginary unit \(i\), where \(i^2 = -1\). This allows us to define the square root of a negative number.
For instance, the square root of \(-4\) is \(2i\) because \((2i)^2 = 4i^2 = 4(-1) = -4\). This transformation is essential in various fields such as engineering, physics, and computer science, providing a comprehensive understanding of complex solutions to equations that involve square roots of negative numbers.
Understanding Square Roots
The concept of square roots is fundamental in mathematics. A square root of a number \( x \) is a number \( r \) such that \( r^2 = x \). Every positive number has two square roots: a positive root and a negative root, which can be written as \( \pm \sqrt{x} \).
The principal square root of a number is the non-negative root. For example, the principal square root of 25 is 5, written as \( \sqrt{25} = 5 \). However, -5 is also a square root of 25 because \((-5)^2 = 25\).
- Positive Square Root: \( \sqrt{x} \)
- Negative Square Root: \( -\sqrt{x} \)
Square Roots of Negative Numbers
Square roots of negative numbers are not real numbers. Instead, they are complex numbers. The square root of a negative number can be written using the imaginary unit \( i \), where \( i = \sqrt{-1} \). For example, the square root of -25 is written as \( \sqrt{-25} = 5i \) because \( (5i)^2 = -25 \).
Properties of Square Roots
- Principal Square Root: For any non-negative number \( x \), the principal square root is the non-negative root, denoted as \( \sqrt{x} \).
- Product Property: The square root of a product is the product of the square roots, \( \sqrt{xy} = \sqrt{x} \cdot \sqrt{y} \) for \( x \geq 0 \) and \( y \geq 0 \).
- Quotient Property: The square root of a quotient is the quotient of the square roots, \( \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}} \) for \( x \geq 0 \) and \( y > 0 \).
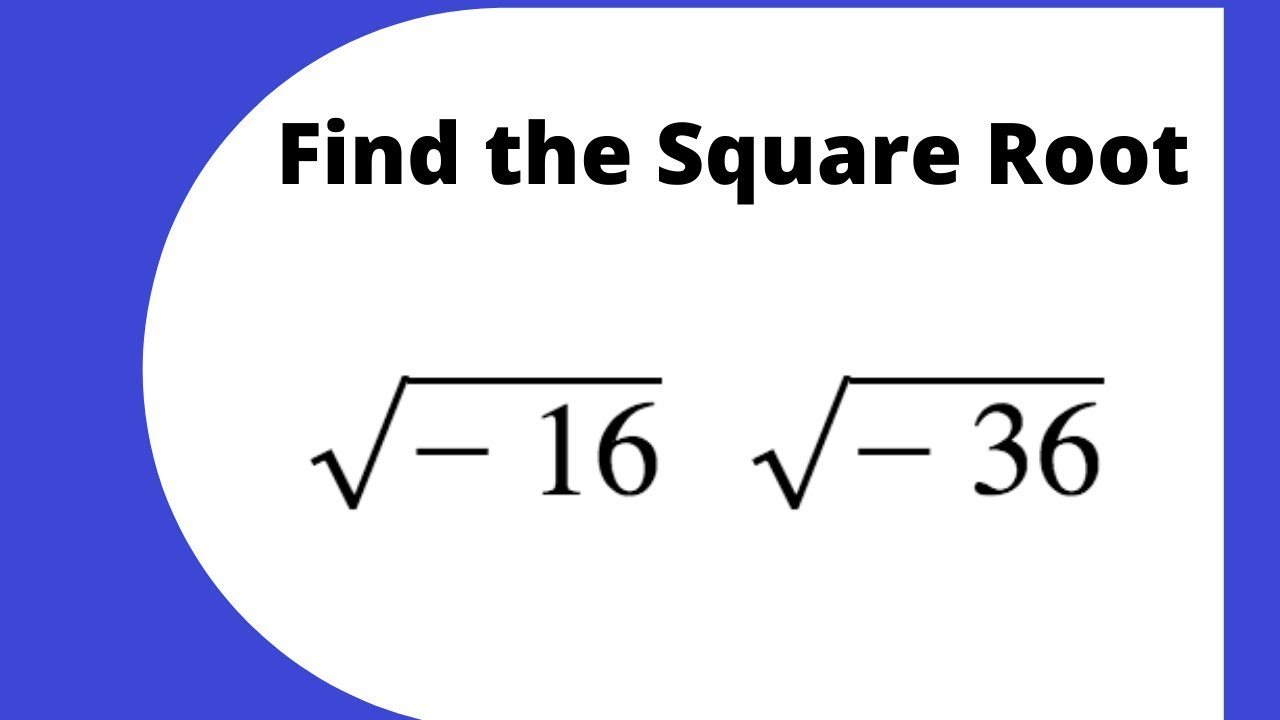
Examples
| Example | Calculation |
| \( \sqrt{36} \) | \( 6 \) (since \( 6^2 = 36 \)) |
| \( -\sqrt{81} \) | \( -9 \) (since \( (-9)^2 = 81 \)) |
| \( \sqrt{-25} \) | \( 5i \) (since \( (5i)^2 = -25 \)) |
Definition of Negative Square Roots
Negative square roots involve the concept of imaginary numbers because the square root of a negative number is not a real number. By definition, the square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). When \( x \) is negative, no real number \( y \) satisfies this equation because the square of a real number is always non-negative.
To handle negative square roots, we introduce the imaginary unit \( i \), where \( i \) is defined as \( \sqrt{-1} \). Using \( i \), the square root of a negative number can be expressed as follows:
- \(\sqrt{-x} = \sqrt{x} \cdot \sqrt{-1} = \sqrt{x} \cdot i\)
Here are some steps to understand the calculation of negative square roots:
- Identify the negative number under the square root. For example, \( \sqrt{-4} \).
- Rewrite the square root by separating the negative sign and the positive part. \( \sqrt{-4} = \sqrt{4} \cdot \sqrt{-1} \).
- Calculate the square root of the positive part. For \( \sqrt{4} = 2 \).
- Multiply by the imaginary unit \( i \). So, \( \sqrt{-4} = 2i \).
This means that the negative square root of \( -4 \) is \( 2i \). In general, for any positive number \( x \), the square root of \( -x \) is \( \sqrt{x}i \).
Imaginary Numbers
Imaginary numbers are a fundamental concept in mathematics, especially when dealing with the square roots of negative numbers. Unlike real numbers, imaginary numbers do not have a place on the conventional number line. Instead, they are used to extend our understanding of number systems.
The imaginary unit, denoted as i, is defined as the square root of -1:
$$i = \sqrt{-1}$$
Using the imaginary unit, we can express the square root of any negative number. For example:
- The square root of -4 is written as $$\sqrt{-4} = 2i$$
- The square root of -9 is written as $$\sqrt{-9} = 3i$$
In general, for any positive real number a, the square root of -a can be expressed as:
$$\sqrt{-a} = i\sqrt{a}$$
This notation helps distinguish between the real and imaginary parts of a number, ensuring clarity and precision in mathematical expressions and computations.
Calculating Negative Square Roots
The concept of calculating the square root of a negative number introduces us to the world of imaginary numbers. In mathematics, the square root of a negative number does not exist within the realm of real numbers. Instead, we use imaginary numbers to define these square roots. The imaginary unit is denoted as \( i \), where \( i = \sqrt{-1} \).
To calculate the square root of a negative number, we follow these steps:
Identify the negative number under the square root. For example, let's consider \( \sqrt{-9} \).
Express the negative number as a product of \(-1\) and a positive number. Here, \(-9\) can be written as \(-1 \times 9\).
Separate the square root into two parts: \( \sqrt{-1 \times 9} \).
Apply the property of square roots to split the expression: \( \sqrt{-1} \times \sqrt{9} \).
Recognize that \( \sqrt{-1} \) is defined as the imaginary unit \( i \), and calculate the square root of the positive number as usual. In this case, \( \sqrt{9} = 3 \).
Combine the results to get \( 3i \). Therefore, \( \sqrt{-9} = 3i \).
This process shows how we use the imaginary unit to calculate the square roots of negative numbers, resulting in imaginary numbers rather than real numbers.

Examples and Applications
Understanding the concept of negative square roots can be enhanced through practical examples and applications. Below are several examples that illustrate how negative square roots are calculated and where they are applied in various fields:
-
Basic Calculation: The square root of a negative number involves imaginary numbers. For example, the square root of -25 is calculated as:
\(\sqrt{-25} = \sqrt{25 \times -1} = \sqrt{25} \times \sqrt{-1} = 5i\)
-
Complex Numbers: In mathematics, complex numbers are used to handle square roots of negative numbers. A complex number has the form \(a + bi\), where \(i\) is the imaginary unit (\(\sqrt{-1}\)). For example, \(3 + 4i\) is a complex number.
-
Electrical Engineering: Imaginary numbers are crucial in the field of electrical engineering, particularly in the analysis of AC circuits. The impedance of a circuit, which may involve inductors and capacitors, is often expressed in terms of complex numbers.
-
Quantum Physics: In quantum mechanics, the wave functions that describe the state of particles are often complex-valued functions. The imaginary unit is fundamental in the Schrödinger equation, which governs the behavior of quantum systems.
-
Signal Processing: In signal processing, Fourier transforms are used to convert signals between time and frequency domains. The calculations involved often require the use of imaginary numbers.
These examples demonstrate that the concept of negative square roots extends beyond simple mathematical curiosity and finds practical applications in various advanced fields.
Real-World Uses of Imaginary Numbers
Imaginary numbers, once considered purely theoretical, have numerous practical applications in various fields. Here are some of the most notable uses:
- Electrical Engineering: Imaginary numbers are fundamental in the analysis of electrical circuits. They are used to describe the behavior of AC (alternating current) circuits, which involve oscillating voltages and currents. The impedance in these circuits, which combines resistance and reactance, is expressed using complex numbers. For example, the impedance \(Z\) can be written as \(Z = R + iX\), where \(R\) is the resistance and \(X\) is the reactance.
- Signal Processing: Imaginary numbers are employed in Fourier transforms, which are essential for signal processing. Fourier transforms decompose signals into their constituent sine and cosine waves, making it possible to analyze frequencies within signals. This is crucial in fields such as telecommunications, audio engineering, and image processing.
- Quantum Physics: In quantum mechanics, the state of a system is described by a wave function, which often involves complex numbers. The Schrödinger equation, a fundamental equation in quantum physics, uses complex numbers to describe how the quantum state of a physical system changes over time.
- Fractals: Complex numbers are used to generate fractals, which are intricate and infinitely detailed patterns. The Mandelbrot set, one of the most famous fractals, is defined using complex numbers. Fractals have applications in computer graphics, modeling natural phenomena, and even in art.
- Control Theory: Imaginary numbers are used in control theory to design and analyze systems such as aircraft autopilots, climate control systems, and industrial automation. They help in determining the stability and response characteristics of these systems.
- Fluid Dynamics: Complex analysis, which involves complex numbers, is used in fluid dynamics to solve problems related to fluid flow. Potential flow theory, for instance, uses complex potential functions to describe fluid motion in various contexts, from aerodynamics to hydrodynamics.
These examples illustrate how imaginary numbers, despite their abstract nature, play a crucial role in solving real-world problems across multiple disciplines.
Common Misconceptions
There are several misconceptions about negative square roots and imaginary numbers that often lead to confusion. Clarifying these can enhance understanding and appreciation of these mathematical concepts.
- Imaginary Numbers Are Not Real: Despite the term "imaginary," these numbers are a valid and crucial part of mathematics, used to solve equations that real numbers cannot.
- Negative Square Roots Have No Practical Use: Contrary to this belief, negative square roots and imaginary numbers are fundamental in fields like engineering, physics, and computer science, solving real-world problems.
- Complex Numbers Are Too Complex: Although they might seem complicated, complex numbers, which include real and imaginary parts, are not inherently difficult to understand and offer powerful tools for mathematical and scientific inquiries.
- Negative Square Roots Do Not Exist: A common misconception is that the square root of a negative number does not exist. This stems from a lack of understanding of imaginary and complex numbers, which provide a framework for these operations.
- Negative Square Roots Lead to Negative Real Numbers: The square root of a negative number introduces the imaginary unit \( i \), not a negative real number. For example, \( \sqrt{-4} \) is \( 2i \), not \(-2\).
- Imaginary Numbers Are Not Useful: Imaginary numbers are crucial in various fields, such as electrical engineering for analyzing AC circuits and quantum mechanics for describing quantum states.
Understanding these misconceptions helps demystify the subject, showcasing the logical structure and practical relevance of negative square roots and complex numbers in mathematics.
| Misconception | Clarification |
|---|---|
| Imaginary Numbers Are Not Real | Imaginary numbers are valid and crucial in mathematics, used to solve equations that real numbers cannot. |
| Negative Square Roots Have No Practical Use | Negative square roots and imaginary numbers are fundamental in fields like engineering and physics. |
| Complex Numbers Are Too Complex | Complex numbers, which include real and imaginary parts, are not inherently difficult to understand. |
| Negative Square Roots Do Not Exist | Imaginary and complex numbers provide a framework for operations involving negative square roots. |
| Negative Square Roots Lead to Negative Real Numbers | Negative square roots introduce the imaginary unit \( i \), not a negative real number. |
| Imaginary Numbers Are Not Useful | Imaginary numbers are crucial in various scientific fields, such as electrical engineering and quantum mechanics. |
Graphing Square Root Functions
Graphing square root functions involves understanding their domain, range, and transformations. The general form of a square root function is:
\( f(x) = \sqrt{a(x - h)} + k \)
Here, \(a\) affects the vertical stretch or compression, \(h\) translates the graph horizontally, and \(k\) translates it vertically.
To graph a square root function, follow these steps:
- Determine the Domain:
- Set the expression inside the square root greater than or equal to zero and solve for \(x\).
- For example, for \( f(x) = \sqrt{x - 2} + 3 \), set \( x - 2 \geq 0 \Rightarrow x \geq 2 \). The domain is \( x \geq 2 \).
- Create a Table of Values:
- Select values of \(x\) within the domain, preferably values that result in perfect squares inside the square root for easy calculation.
- For \( f(x) = \sqrt{x - 2} + 3 \), choose \(x = 2, 3, 6, 11\) for simplicity.
- Calculate corresponding \(y\) values:
x y 2 3 3 4 6 5 11 6 - Plot the Points:
- Using graph paper or graphing software, plot the points from the table.
- Mark the points \((2, 3)\), \((3, 4)\), \((6, 5)\), and \((11, 6)\) on the coordinate plane.
- Draw the Curve:
- Connect the points with a smooth curve, starting from the leftmost point and extending to the right.
- Ensure the curve reflects the shape typical of square root functions, which starts at the boundary point and increases slowly.
Graphing transformations can shift the graph vertically and horizontally:
- Vertical Shifts: The term \(+ k\) moves the graph up by \(k\) units.
- Horizontal Shifts: The term \((x - h)\) moves the graph right by \(h\) units.
- Vertical Stretch/Compression: The coefficient \(a\) affects the steepness. If \( |a| > 1 \), the graph stretches; if \( 0 < |a| < 1 \), it compresses.
Example: For \( f(x) = \sqrt{x - 2} + 3 \), the graph starts at \((2, 3)\) and moves upward as \(x\) increases, reflecting the horizontal shift of 2 units to the right and a vertical shift of 3 units up.
Graphing square root functions requires careful plotting and understanding of transformations to ensure accurate representation.

Conclusion
Understanding the concept of negative square roots and imaginary numbers is crucial in expanding our mathematical knowledge. By introducing the imaginary unit \(i\), defined as \(\sqrt{-1}\), we can handle the square roots of negative numbers, which cannot be addressed using real numbers alone.
Throughout this guide, we have explored the definition, calculation, and applications of negative square roots. Imaginary numbers play a pivotal role in various mathematical fields, including algebra, calculus, and complex analysis. They also have practical applications in physics, engineering, and signal processing, showcasing their importance beyond theoretical mathematics.
One common misconception is that the square root of a negative number is not possible. However, by using the imaginary unit, we see that it is not only possible but also opens up a whole new realm of complex numbers. These numbers are essential for solving certain equations and understanding advanced mathematical concepts.
The journey through negative square roots and imaginary numbers demonstrates the beauty and depth of mathematics. It shows how extending our number system to include complex numbers allows us to solve problems that were previously insurmountable. Embracing these concepts enhances our problem-solving skills and provides a deeper appreciation for the interconnectedness of different mathematical areas.
As we conclude, remember that the world of mathematics is vast and ever-expanding. The exploration of negative square roots and imaginary numbers is just one part of this fascinating journey. By continuing to study and apply these concepts, we can unlock new possibilities and contribute to advancements in science and technology.
In summary, the understanding and application of negative square roots through imaginary numbers are fundamental to advancing in both theoretical and applied mathematics. This comprehensive guide has provided a solid foundation, and we encourage further exploration and study to fully appreciate the power and elegance of these mathematical concepts.
Hướng dẫn chi tiết cách tìm căn bậc hai của số âm bằng cách sử dụng đơn vị ảo i. Xem ngay video để hiểu rõ hơn.
Cách Tìm Căn Bậc Hai của Số Âm - Video Hướng Dẫn
READ MORE:
Video giải thích lý do vì sao không thể tính căn bậc hai của số âm và cách hiểu đúng về vấn đề này. Xem ngay để tìm hiểu thêm.
Tại sao không thể tính căn bậc hai của số âm?