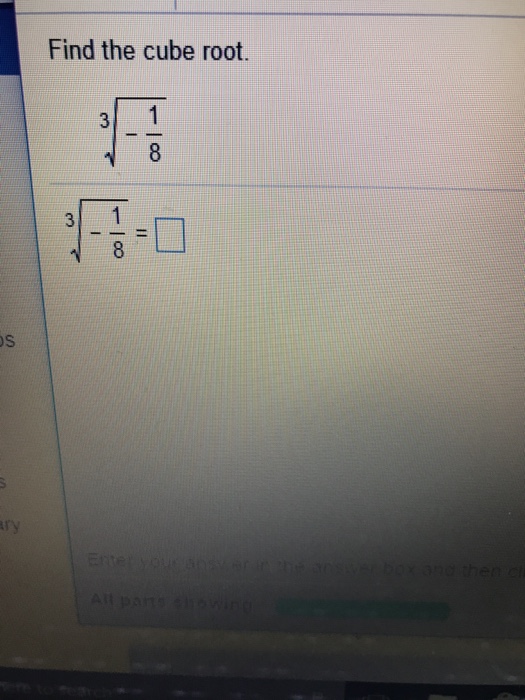
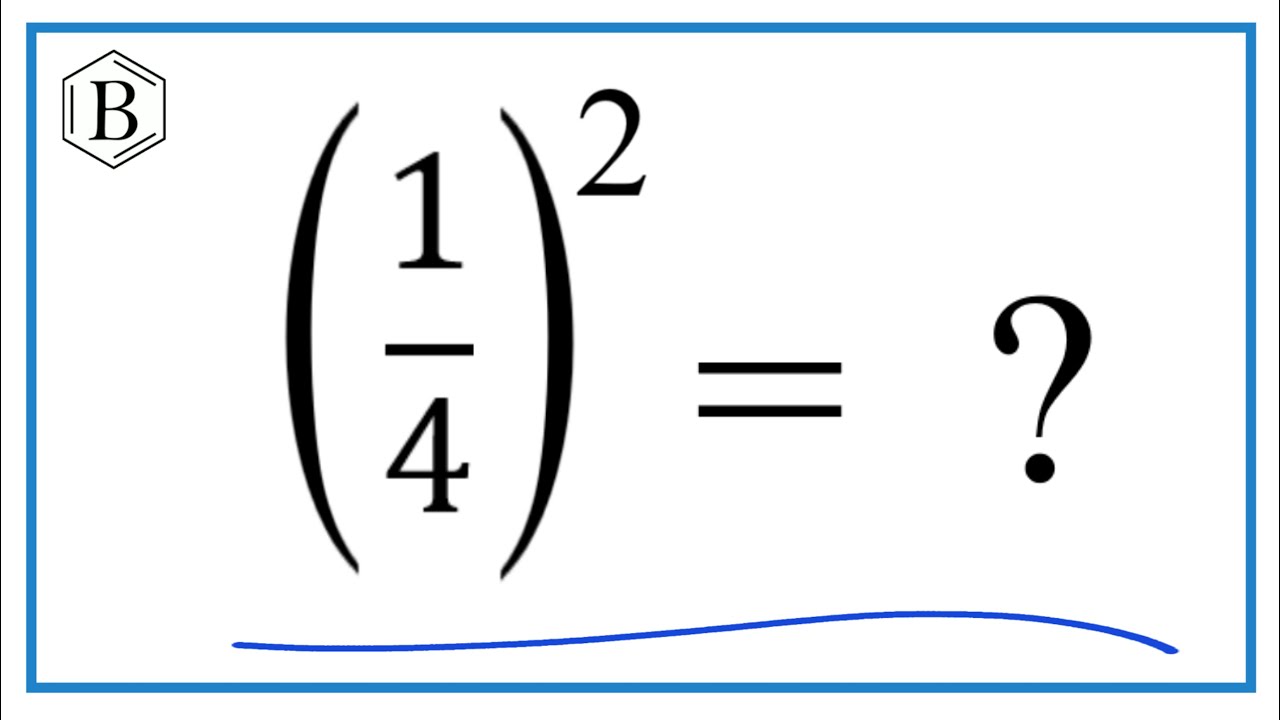Topic square root of 1/9th: Understanding the square root of 1/9 can simplify many mathematical problems. This guide will walk you through the step-by-step simplification process, explore practical applications, and provide insights into how this fundamental concept is used in various mathematical contexts. Dive in to enhance your comprehension and appreciation of this essential mathematical operation.
Table of Content
- Understanding the Square Root of 1/9
- Introduction to Square Roots
- Basic Concepts of Square Roots
- Understanding Fractions and Square Roots
- Step-by-Step Simplification of √1/9
- Mathematical Explanation and Formula
- Visual Representation and Graphs
- Decimal Representation of √1/9
- Real-World Applications of √1/9
- Common Mistakes and Pitfalls
- Advanced Topics: Roots and Powers
- Online Calculators and Tools
- Additional Resources and Further Reading
- Frequently Asked Questions (FAQs)
- Conclusion and Summary
- YOUTUBE: Hướng dẫn cách xấp xỉ căn bậc hai của một số để thu hút người xem và cải thiện kỹ năng toán học của bạn.
Understanding the Square Root of 1/9
The square root of a fraction is determined by taking the square root of the numerator and the denominator separately. For the fraction 1/9, we find the square root of both 1 and 9.
Steps to Simplify the Square Root of 1/9
- Identify the fraction: \(\frac{1}{9}\)
- Rewrite the fraction under a single square root: \(\sqrt{\frac{1}{9}}\)
- Split the square root into the numerator and the denominator: \(\frac{\sqrt{1}}{\sqrt{9}}\)
- Calculate the square roots separately:
- \(\sqrt{1} = 1\)
- \(\sqrt{9} = 3\)
- Combine the results: \(\frac{1}{3}\)
Result
The square root of 1/9 is:
\(\sqrt{\frac{1}{9}} = \frac{1}{3}\)
In decimal form, this is approximately 0.3333.
Visual Representation
| Fraction | Square Root | Decimal Form |
|---|---|---|
| \(\frac{1}{9}\) | \(\frac{1}{3}\) | 0.3333 |
Additional Information
The calculation of square roots can be applied to other fractions similarly by taking the square root of the numerator and the denominator individually. This method simplifies understanding and solving square root problems involving fractions.
Useful Links

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics, offering a way to find a number which, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\). This principle extends to fractions as well, such as finding the square root of \( \frac{1}{9} \).
To understand the square root of \( \frac{1}{9} \), we follow these steps:
- Recognize that the square root of a fraction can be expressed as the square root of the numerator divided by the square root of the denominator. Thus, \( \sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} \).
- Simplify each square root separately. The square root of 1 is 1, and the square root of 9 is 3. Therefore, \( \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3} \).
- Combine the simplified terms to get the final result. Hence, \( \sqrt{\frac{1}{9}} = \frac{1}{3} \).
This process not only helps in simplifying the square root of fractions but also reinforces the understanding of basic arithmetic operations involving square roots.
Basic Concepts of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol √. For instance, the square root of 9 is 3, because 3 × 3 = 9.
- The square root of 1/9 can be represented as √(1/9).
- This can be rewritten as the division of square roots: √1 / √9.
- Since the square root of 1 is 1 and the square root of 9 is 3, we have √(1/9) = 1/3.
To simplify the square root of a fraction:
- Identify the numerator and denominator of the fraction.
- Take the square root of both the numerator and the denominator separately.
- Divide the square root of the numerator by the square root of the denominator.
Here is a more general example:
| Fraction | Square Root |
|---|---|
| 1/4 | √(1/4) = 1/2 |
| 1/16 | √(1/16) = 1/4 |
| 1/25 | √(1/25) = 1/5 |
Understanding these basic principles can help in simplifying and working with square roots effectively.
Understanding Fractions and Square Roots
Fractions and square roots are fundamental concepts in mathematics. Understanding how to simplify and work with these can make complex problems more manageable. Let's explore how to handle square roots of fractions, such as the square root of 1/9th, step by step.
To find the square root of a fraction, follow these steps:
- Identify the numerator and the denominator of the fraction. For 1/9, the numerator is 1 and the denominator is 9.
- Take the square root of both the numerator and the denominator separately. The square root of 1 is 1, and the square root of 9 is 3.
- Divide the square root of the numerator by the square root of the denominator: \(\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3}\).
Here is a table summarizing the process for different fractions:
| Fraction | Square Root |
|---|---|
| 1/4 | \(\sqrt{\frac{1}{4}} = \frac{1}{2}\) |
| 1/16 | \(\sqrt{\frac{1}{16}} = \frac{1}{4}\) |
| 1/25 | \(\sqrt{\frac{1}{25}} = \frac{1}{5}\) |
This method shows that the square root of a fraction can be simplified by taking the square roots of the numerator and the denominator separately. By following these steps, you can easily handle square roots of other fractions and understand the basic principles behind them.
Step-by-Step Simplification of √1/9
Simplifying the square root of 1/9 involves a few straightforward steps. This process will help you understand how to handle square roots of fractions.
-
Identify the fraction under the square root:
The given expression is \( \sqrt{\frac{1}{9}} \).
-
Separate the numerator and the denominator:
We can rewrite the square root of a fraction as the fraction of the square roots: \( \frac{\sqrt{1}}{\sqrt{9}} \).
-
Simplify the square roots:
- \( \sqrt{1} = 1 \)
- \( \sqrt{9} = 3 \)
-
Combine the simplified parts:
Now, place the simplified numerator and denominator back into the fraction: \( \frac{1}{3} \).
-
Result:
The simplified form of \( \sqrt{\frac{1}{9}} \) is \( \frac{1}{3} \) or approximately 0.333.

Mathematical Explanation and Formula
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical terms, if \( x^2 = y \), then \( x \) is the square root of \( y \). This concept can be applied to both whole numbers and fractions.
To find the square root of a fraction, we use the property of square roots that states:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
Let's apply this to the fraction \( \frac{1}{9} \):
- Identify the numerator and denominator of the fraction. Here, the numerator \( a = 1 \) and the denominator \( b = 9 \).
- Take the square root of the numerator: \(\sqrt{1} = 1\).
- Take the square root of the denominator: \(\sqrt{9} = 3\).
- Express the square root of the fraction as the fraction of the square roots: \(\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3}\).
Therefore, the square root of \( \frac{1}{9} \) is \(\frac{1}{3}\), which can also be represented as a decimal, approximately 0.333.
This method can be generalized to any fraction where both the numerator and the denominator are perfect squares. If either is not a perfect square, the result may be an irrational number.
Visual Representation and Graphs
Visualizing the square root of a fraction like \( \frac{1}{9} \) helps in understanding its mathematical properties and applications. Below is a step-by-step guide to the visual representation and graphing of \( \sqrt{\frac{1}{9}} \).
First, let's simplify \( \sqrt{\frac{1}{9}} \):
- Recognize that \( \sqrt{\frac{1}{9}} \) can be written as \( \frac{\sqrt{1}}{\sqrt{9}} \).
- Simplify the square roots: \( \sqrt{1} = 1 \) and \( \sqrt{9} = 3 \).
- Thus, \( \sqrt{\frac{1}{9}} = \frac{1}{3} \).
To graph this, consider the function \( y = \sqrt{x} \). For \( x = \frac{1}{9} \), the value of \( y \) will be \( \frac{1}{3} \).
Here’s a table of values for the square root function:
| x | 0 | \(\frac{1}{9}\) | \(\frac{1}{4}\) | 1 | 4 | 9 |
| y = \(\sqrt{x}\) | 0 | \(\frac{1}{3}\) | \(\frac{1}{2}\) | 1 | 2 | 3 |
The graph of \( y = \sqrt{x} \) passes through the point \( \left( \frac{1}{9}, \frac{1}{3} \right) \), illustrating the relationship between the fraction and its square root.
Using graphing tools like Desmos or other graphing calculators, you can visualize this function and observe how it behaves as \( x \) varies. The graph below illustrates the function \( y = \sqrt{x} \), highlighting the point \( \left( \frac{1}{9}, \frac{1}{3} \right) \).
Understanding the visual representation of square roots, especially for fractions, is crucial in various fields such as algebra, geometry, and real-world applications. Graphing these functions helps to better grasp their behavior and the effects of different inputs.
Decimal Representation of √1/9
The square root of a number is a value that, when multiplied by itself, gives the original number. To find the decimal representation of the square root of 1/9, we need to follow a few simple steps.
- Understand the square root of a fraction: The square root of a fraction can be found by taking the square root of the numerator and the square root of the denominator separately. For the fraction 1/9:
- Numerator: 1
- Denominator: 9
- Calculate the square root of the numerator: The square root of 1 is 1, because 1 × 1 = 1.
- Calculate the square root of the denominator: The square root of 9 is 3, because 3 × 3 = 9.
- Form the fraction: The square root of 1/9 is the fraction formed by the square roots of the numerator and the denominator:
- √1/9 = √1 / √9 = 1 / 3
- Convert to decimal: The fraction 1/3 can be converted to a decimal by dividing 1 by 3:
- 1 ÷ 3 = 0.333...
Thus, the decimal representation of √1/9 is 0.333..., which is a repeating decimal and can be written as 0.3.
Real-World Applications of √1/9
The square root of 1/9, which is \( \frac{1}{3} \), has several practical applications in various fields. Here are some examples:
-
Mathematics and Education:
Understanding the concept of square roots is fundamental in math education. The simplicity of \( \sqrt{\frac{1}{9}} = \frac{1}{3} \) serves as an excellent teaching tool for introducing students to the properties of square roots and fractions. This basic example helps in grasping more complex algebraic principles.
-
Engineering and Physics:
Square roots are commonly used in engineering and physics to solve equations related to areas, volumes, and other properties of physical objects. For instance, in designing components where specific dimensions and tolerances are crucial, knowing the exact values such as \( \frac{1}{3} \) derived from \( \sqrt{\frac{1}{9}} \) can be important for precision.
-
Statistics:
In statistics, square roots are used to normalize data. The square root transformation can stabilize the variance of data and make it more normally distributed, which is useful for various statistical analyses. For instance, if a dataset includes values such as \( \frac{1}{9} \), transforming it using its square root \( \frac{1}{3} \) can simplify the analysis process.
-
Financial Calculations:
In finance, understanding and applying square roots is essential in risk management and option pricing models. For example, the volatility of asset returns is often represented as the square root of the variance. Simplifying terms like \( \frac{1}{9} \) to \( \frac{1}{3} \) aids in these financial models and calculations.
-
Computer Graphics:
Square roots are used in computer graphics for various calculations, including distances and normalization of vectors. Knowing precise values such as \( \frac{1}{3} \) from \( \sqrt{\frac{1}{9}} \) helps in rendering images accurately and efficiently.
These examples illustrate that the square root of a fraction like \( \frac{1}{9} \) has wide-ranging applications beyond simple arithmetic, playing a critical role in different scientific and practical fields.

Common Mistakes and Pitfalls
When dealing with the square root of , it's easy to make certain mistakes. Here are some common errors and how to avoid them:
- Incorrect Simplification: One common mistake is not simplifying the square root correctly. Remember that can be rewritten as , which simplifies to .
- Misinterpreting the Result: Another error is misinterpreting the result as a whole number instead of a fraction. The correct simplified form is or approximately 0.333.
- Forgetting the Negative Root: While typically refers to the principal (positive) square root, it's important to note that there are always two roots: and .
- Incorrectly Handling Radicals: Be cautious with operations involving radicals. For example, should not be confused with . They simplify differently.
- Misapplying Rules: Make sure not to apply rules incorrectly. For instance, the property = is valid, but ensure it is used correctly in the context of the problem.
By being aware of these common pitfalls, you can avoid errors and correctly handle the square root of in various mathematical contexts.
Advanced Topics: Roots and Powers
Understanding the advanced concepts of roots and powers involves delving into the relationships and properties that connect these mathematical operations. Here, we will explore various advanced topics related to the square root of 1/9, rational exponents, and their applications.
Rational Exponents
Rational exponents are a way to express roots as exponents. The general form is:
\[
a^{\frac{m}{n}} = \sqrt[n]{a^m}
\]
For example, the square root of 1/9 can be written as:
\[
\left(\frac{1}{9}\right)^{\frac{1}{2}} = \sqrt{\frac{1}{9}}
\]
This notation helps simplify complex calculations and makes it easier to manipulate expressions involving roots.
Properties of Exponents
When dealing with exponents, several key properties can be very useful:
- Product of Powers: \(a^m \cdot a^n = a^{m+n}\)
- Quotient of Powers: \(\frac{a^m}{a^n} = a^{m-n}\)
- Power of a Power: \((a^m)^n = a^{mn}\)
- Power of a Product: \((ab)^m = a^m \cdot b^m\)
- Power of a Quotient: \(\left(\frac{a}{b}\right)^m = \frac{a^m}{b^m}\)
Applying Properties to Roots
Using these properties, we can simplify expressions involving roots. For example:
\[
\sqrt{\frac{1}{9}} = \left(\frac{1}{9}\right)^{\frac{1}{2}} = \frac{1^{\frac{1}{2}}}{9^{\frac{1}{2}}} = \frac{1}{3}
\]
This shows how the properties of exponents simplify the calculation of the square root of a fraction.
Negative and Fractional Exponents
Exponents can also be negative or fractional, expanding the range of possible expressions:
- Negative Exponents: \(a^{-n} = \frac{1}{a^n}\)
- Fractional Exponents: \(a^{\frac{m}{n}} = \sqrt[n]{a^m}\)
For instance:
\[
9^{-\frac{1}{2}} = \frac{1}{9^{\frac{1}{2}}} = \frac{1}{3}
\]
Applications in Solving Equations
These advanced concepts are particularly useful in solving equations involving roots and powers. For example, to solve for \(x\) in the equation:
\[
x^{\frac{3}{2}} = 8
\]
We can raise both sides to the reciprocal power of \(\frac{2}{3}\):
\[
\left(x^{\frac{3}{2}}\right)^{\frac{2}{3}} = 8^{\frac{2}{3}} \implies x = \sqrt[3]{8^2} = \sqrt[3]{64} = 4
\]
Conclusion
Understanding the advanced properties of roots and powers allows for more efficient and elegant solutions to complex mathematical problems. By mastering these concepts, one can gain deeper insights into the structure and behavior of mathematical expressions.
Online Calculators and Tools
Calculating square roots, especially for fractions like
-
Basic Scientific Calculators:
Most scientific calculators, whether physical or digital, have a square root function. These calculators can quickly compute square roots, including those of fractions like
\(\frac{1}{9}\). Simply input \(\sqrt{(1/9)}\) and the calculator will provide the result. -
Online Calculators:
Several websites offer free tools to compute square roots. These online calculators provide step-by-step solutions, helping users understand the calculation process. Websites like and are excellent resources for this purpose.
-
Math Software:
Programs such as MATLAB, Mathematica, and Python (using libraries like NumPy) are capable of handling complex square root calculations. These tools are widely used in educational and professional settings for their advanced functionalities.
-
Mobile Apps:
There are many educational apps available on smartphones and tablets that offer interactive ways to learn and calculate square roots. Apps such as Photomath and Mathway provide step-by-step solutions and are user-friendly.
-
Spreadsheet Programs:
Software like Microsoft Excel and Google Sheets have built-in functions for square root calculations. For example, using the formula
=SQRT(1/9)in a cell will yield the result\(\frac{1}{3}\) . These tools are particularly useful for financial and statistical analysis.
Using these tools can simplify the process of finding square roots and enhance understanding through visual aids and detailed explanations. They are indispensable for both students and professionals aiming to improve their mathematical skills.
Additional Resources and Further Reading
For those who wish to dive deeper into the topic of square roots and their applications, here are some valuable resources and further reading materials:
-
This comprehensive guide covers various topics related to exponents and radicals, including detailed explanations and interactive exercises on simplifying square roots, which can help reinforce your understanding of √1/9.
-
OpenStax offers free, peer-reviewed, openly licensed textbooks that are ideal for learning about square roots, fractions, and other mathematical concepts in depth.
-
This resource focuses on the graphical interpretation and practical applications of mathematical functions, including square roots, which can provide a deeper understanding of how these concepts are used in real-world scenarios.
-
An easy-to-understand resource that covers the basics and advanced topics related to exponents and logarithms, including the principles underlying square roots like √1/9.
-
Coursera offers a variety of online courses in algebra from top universities, providing in-depth lessons and exercises on exponents, radicals, and other fundamental concepts.

Frequently Asked Questions (FAQs)
Here are some common questions related to the square root of \( \frac{1}{9} \):
-
What is the square root of \( \frac{1}{9} \)?
The square root of \( \frac{1}{9} \) is \( \frac{1}{3} \), because \( \left( \frac{1}{3} \right)^2 = \frac{1}{9} \).
-
Is \( \frac{1}{3} \) a rational number?
Yes, \( \frac{1}{3} \) is a rational number because it can be expressed as the quotient of two integers (1 and 3).
-
How can I verify the square root of \( \frac{1}{9} \) manually?
To verify manually, you can square \( \frac{1}{3} \) and check if the result is \( \frac{1}{9} \). Indeed, \( \left( \frac{1}{3} \right)^2 = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9} \).
-
What is the decimal representation of the square root of \( \frac{1}{9} \)?
The decimal representation of \( \frac{1}{3} \) is approximately 0.3333 (repeating).
-
How is the square root of a fraction calculated?
The square root of a fraction \( \frac{a}{b} \) is calculated by taking the square root of the numerator and the denominator separately: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
-
Can the square root of \( \frac{1}{9} \) be negative?
Yes, the square root of \( \frac{1}{9} \) can be negative. The principal square root is \( \frac{1}{3} \), but \( -\frac{1}{3} \) is also a square root since \( \left( -\frac{1}{3} \right)^2 = \frac{1}{9} \).
-
Why is it important to understand square roots of fractions?
Understanding square roots of fractions is crucial in various mathematical fields including algebra, calculus, and in solving real-world problems where ratios and proportions are involved.
Conclusion and Summary
The square root of \( \frac{1}{9} \) is a simple yet intriguing mathematical concept that has various implications and applications. Throughout this guide, we've explored multiple facets of this topic, from basic definitions to advanced mathematical operations. Let's summarize the key points:
- Basic Definition: The square root of \( \frac{1}{9} \) is \( \frac{1}{3} \). This is because \( \left( \frac{1}{3} \right)^2 = \frac{1}{9} \).
- Simplification Process: Simplifying square roots of fractions involves taking the square root of both the numerator and the denominator separately.
- Decimal Representation: The decimal form of \( \frac{1}{3} \) is approximately 0.3333, a repeating decimal.
- Visual Representation: Graphical representations can help in understanding the concept better, particularly on a number line or through geometric shapes.
- Real-World Applications: The concept finds use in various fields, such as engineering, physics, and finance, where precise calculations and simplifications are necessary.
- Common Mistakes: One common error is misinterpreting the square root of fractions by not simplifying the components correctly.
- Advanced Topics: Understanding how roots and powers interact can deepen comprehension, particularly in higher-level mathematics and applied sciences.
In conclusion, the square root of \( \frac{1}{9} \) is a fundamental concept that, while straightforward, provides a gateway to more complex mathematical ideas and practical applications. Mastery of this topic is crucial for anyone looking to advance in mathematics or related fields.
Hướng dẫn cách xấp xỉ căn bậc hai của một số để thu hút người xem và cải thiện kỹ năng toán học của bạn.
Cách Xấp Xỉ Căn Bậc Hai của Một Số
READ MORE:
Hướng dẫn cách đơn giản hóa căn bậc hai để thu hút người xem và nâng cao kỹ năng toán học của bạn.
Cách Đơn Giản Hóa Căn Bậc Hai