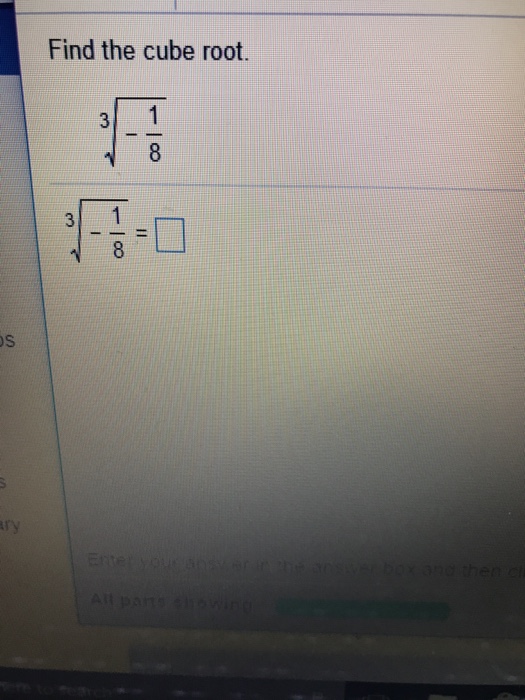
Topic negative square root of a number: The negative square root of a number introduces the concept of imaginary numbers, a fundamental part of complex numbers. This article explores what the negative square root means, how to calculate it, and its applications in various fields. Understanding these concepts is essential for advanced mathematics and real-world problem-solving.
Table of Content
- Understanding the Negative Square Root of a Number
- Introduction to Square Roots
- Understanding Negative Square Roots
- Imaginary Numbers and Their Properties
- Simplifying the Square Root of a Negative Number
- Examples and Applications
- Common Misconceptions
- Practical Exercises
- YOUTUBE: Video hướng dẫn cách tìm căn bậc hai của số âm, giải thích khái niệm và các bước thực hiện một cách dễ hiểu.
Understanding the Negative Square Root of a Number
The concept of the negative square root is fundamental in mathematics, particularly in the study of complex numbers. This guide will help you understand how to simplify and work with the square root of negative numbers.
Definition and Basic Concept
The square root of a negative number involves the imaginary unit \(i\), which is defined as:
\[
i = \sqrt{-1}
\]
For any positive real number \(p\), the square root of \(-p\) is expressed as:
\[
\sqrt{-p} = i\sqrt{p}
\]
Examples
-
For \(p = 4\):
\[
\sqrt{-4} = i\sqrt{4} = i \cdot 2 = 2i
\] -
For \(p = 9\):
\[
\sqrt{-9} = i\sqrt{9} = i \cdot 3 = 3i
\]
Principal Square Root
The principal square root of a negative number \(-p\) is \(i\sqrt{p}\), which ensures we are taking the positive imaginary part.
Square Roots of Products
It is important to note that the property \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\) does not hold for negative numbers. For example:
\[
\sqrt{-4 \cdot -9} \neq \sqrt{-4} \cdot \sqrt{-9}
\]
Instead, you would handle each negative part separately with the imaginary unit:
\[
\sqrt{(-1) \cdot 4 \cdot (-1) \cdot 9} = \sqrt{(-1)^2 \cdot 36} = \sqrt{36} = 6
\]
Complex Solutions
When solving equations involving square roots of negative numbers, such as \(x^2 = -4\), the solutions are:
\[
x = \pm \sqrt{-4} = \pm 2i
\]
Practical Applications
Understanding the square root of negative numbers is crucial in fields such as engineering, physics, and computer science where complex numbers are used to solve real-world problems.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics. A square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). For example, the square root of 9 is 3, since \( 3 \times 3 = 9 \). This idea extends to both positive and negative numbers. For instance, both 3 and -3 are square roots of 9 because \( (-3) \times (-3) = 9 \).
To denote the square root, we use the radical symbol \( \sqrt{} \). When you see \( \sqrt{9} \), it means the square root of 9, which is 3. However, it’s important to note that by convention, the radical symbol refers to the principal (non-negative) square root.
Square roots are not always whole numbers. For example, the square root of 2 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal form goes on forever without repeating.
Negative numbers do not have real square roots because no real number squared will result in a negative number. Instead, the square roots of negative numbers are called imaginary numbers, denoted with the imaginary unit \( i \), where \( i = \sqrt{-1} \). For example, the square root of -9 is written as \( 3i \).
Understanding square roots is crucial for various mathematical applications, including solving quadratic equations, simplifying expressions, and understanding geometric concepts.
Understanding Negative Square Roots
When we talk about square roots, we often refer to the positive root of a given number. However, when it comes to negative numbers under the square root, things get more interesting as we enter the realm of complex numbers. This section explores the concept of negative square roots and how they can be understood using imaginary numbers.
In mathematics, the square root of a negative number does not exist within the set of real numbers because no real number squared will result in a negative value. For example, there is no real number x such that x2 = -4. To address this, mathematicians use imaginary numbers.
The imaginary unit, denoted as i, is defined by the property that i2 = -1. Using this definition, the square root of any negative number can be expressed in terms of i. For example:
- The square root of -1 is i, because i2 = -1.
- The square root of -4 is 2i, since (2i)2 = 4i2 = 4(-1) = -4.
- In general, the square root of -p (where p is a positive real number) is given by √(-p) = i√(p).
This approach allows us to handle square roots of negative numbers systematically. For instance, if we want to find the square root of -25, we can proceed as follows:
- Express -25 as the product of -1 and 25: -25 = -1 * 25.
- Take the square root of each factor: √(-25) = √(-1) * √(25).
- Use the definition of the imaginary unit: √(-1) = i and √(25) = 5.
- Combine the results: √(-25) = 5i.
Thus, the square root of -25 is 5i. Imaginary numbers are crucial in various fields of mathematics and engineering, particularly in complex analysis, electrical engineering, and quantum mechanics, where they help solve problems involving square roots of negative numbers.
Understanding negative square roots is essential for progressing to more advanced mathematical concepts, as it lays the groundwork for working with complex numbers, which combine real and imaginary parts. The general form of a complex number is a + bi, where a and b are real numbers.
Imaginary Numbers and Their Properties
Imaginary numbers are a fundamental concept in mathematics, extending the real number system to solve equations that have no real solutions. The imaginary unit is denoted by \(i\), defined as \(i = \sqrt{-1}\). This allows the expression of the square root of any negative number. Imaginary numbers are essential in various fields such as engineering, physics, and complex number theory.
Here are some key properties of imaginary numbers:
- Imaginary Unit: \(i\) is defined such that \(i^2 = -1\).
- Multiplication: When multiplying imaginary numbers, the imaginary unit's properties are used, e.g., \(i \times i = -1\).
- Complex Numbers: Any complex number can be expressed in the form \(a + bi\), where \(a\) and \(b\) are real numbers, and \(i\) is the imaginary unit.
To understand the square root of negative numbers, consider the following steps:
- Identify the negative number, say \(-x\).
- Express it as \(\sqrt{-x} = \sqrt{(-1) \times x}\).
- Using the property of \(i\), rewrite it as \(\sqrt{-x} = i \sqrt{x}\).
For example, to find \(\sqrt{-25}\), we proceed as:
| \(\sqrt{-25}\) | = \(\sqrt{(-1) \times 25}\) |
| = \(i \sqrt{25}\) | |
| = \(i \times 5\) | |
| = \(5i\) |
Thus, \(\sqrt{-25} = 5i\). This illustrates how imaginary numbers extend our number system to handle the square roots of negative numbers effectively.
Simplifying the Square Root of a Negative Number
The square root of a negative number involves imaginary numbers, denoted by the symbol \(i\), where \(i\) is defined as \(\sqrt{-1}\). Simplifying the square root of a negative number is straightforward when you follow these steps:
- Identify the negative number under the square root.
- Separate the negative sign from the number. For example, \(\sqrt{-9}\) becomes \(\sqrt{-1 \cdot 9}\).
- Use the property \(\sqrt{-1} = i\). Therefore, \(\sqrt{-1 \cdot 9}\) becomes \(i \sqrt{9}\).
- Simplify the square root of the positive number. In this case, \(\sqrt{9} = 3\).
- Combine the results to get the final answer. So, \(\sqrt{-9} = 3i\).
Thus, any negative square root can be expressed as an imaginary number. For example:
- \(\sqrt{-4} = 2i\)
- \(\sqrt{-16} = 4i\)
- \(\sqrt{-25} = 5i\)
This method can be applied to any negative number to find its square root in terms of \(i\), making complex numbers easier to handle in various mathematical problems.

Examples and Applications
Understanding the square root of negative numbers is crucial in various mathematical contexts, especially when dealing with complex numbers. Here are detailed examples and applications to illustrate these concepts:
- Example 1: Simplifying
- Identify the negative sign inside the square root:
- Express as a product of and :
- Apply the square root to each component:
- Result:
- Example 2: Solving
- Isolate the variable:
- Simplify:
- Application in Engineering:
In electrical engineering, the concept of imaginary numbers is used to analyze AC circuits. For example, impedance in a circuit with resistance (R) and inductive reactance (XL) can be represented as a complex number: .
- Application in Control Systems:
Imaginary numbers are used in control systems to determine the stability of systems. The roots of the characteristic equation of a system can be complex, and their imaginary parts indicate oscillatory behavior.
Common Misconceptions
Understanding the square root of negative numbers and imaginary numbers can be challenging. Here are some common misconceptions and clarifications to help clear up the confusion.
- Misconception 1: Negative numbers have no square roots.
- Misconception 2: Imaginary numbers are not "real" or useful.
- Misconception 3: The square root of a negative number is negative.
- Misconception 4: Imaginary numbers behave the same as real numbers.
- Misconception 5: Complex numbers have no practical applications.
It's often thought that negative numbers cannot have square roots because no real number squared results in a negative number. However, the concept of imaginary numbers, denoted by i, allows for the square root of negative numbers. The imaginary unit i is defined such that i² = -1.
Despite their name, imaginary numbers are essential in various fields, including engineering, physics, and complex number theory. They are used to solve equations that have no real solutions and to perform calculations in signal processing and AC circuit analysis.
When simplifying the square root of a negative number, the result is not a negative real number but rather an imaginary number. For example, , not -3.
Imaginary numbers follow different rules than real numbers, particularly in multiplication. For example, , and their addition, subtraction, multiplication, and division are governed by the properties of complex numbers.
Complex numbers, which consist of a real part and an imaginary part, are widely used in practical applications. They are crucial in electrical engineering for analyzing AC circuits, in control theory, quantum mechanics, and even in fractal geometry, as seen in the Mandelbrot set.
Practical Exercises
In this section, we will work through several practical exercises to solidify our understanding of the negative square root of a number and its applications. Follow the steps for each exercise to practice and enhance your skills.
-
Exercise 1: Simplifying \(\sqrt{-16}\)
- Step 1: Recognize that \(\sqrt{-16}\) involves the square root of a negative number.
- Step 2: Express the negative number as the product of -1 and a positive number: \(\sqrt{-16} = \sqrt{-1 \times 16}\).
- Step 3: Use the property of square roots to separate the terms: \(\sqrt{-1 \times 16} = \sqrt{-1} \times \sqrt{16}\).
- Step 4: Simplify \(\sqrt{16}\) which is 4, and recall that \(\sqrt{-1} = i\): \(\sqrt{-16} = 4i\).
- Answer: \(4i\).
-
Exercise 2: Solving Quadratic Equation with Complex Roots
- Step 1: Consider the quadratic equation \(x^2 + 4 = 0\).
- Step 2: Isolate \(x^2\): \(x^2 = -4\).
- Step 3: Take the square root of both sides: \(x = \pm\sqrt{-4}\).
- Step 4: Simplify using \(i\): \(x = \pm 2i\).
- Answer: \(x = 2i\) or \(x = -2i\).
-
Exercise 3: Adding Complex Numbers
- Step 1: Add the real parts and the imaginary parts separately. Consider the numbers \(3 + 2i\) and \(1 - 4i\).
- Step 2: Add the real parts: \(3 + 1 = 4\).
- Step 3: Add the imaginary parts: \(2i - 4i = -2i\).
- Answer: \(4 - 2i\).
-
Exercise 4: Multiplying Complex Numbers
- Step 1: Use the distributive property to multiply \((2 + 3i)(1 - 4i)\).
- Step 2: Expand the expression: \(2(1) + 2(-4i) + 3i(1) + 3i(-4i)\).
- Step 3: Simplify each term: \(2 - 8i + 3i - 12i^2\).
- Step 4: Recall that \(i^2 = -1\), so \( -12i^2 = 12\).
- Step 5: Combine like terms: \(2 - 8i + 3i + 12 = 14 - 5i\).
- Answer: \(14 - 5i\).
-
Exercise 5: Dividing Complex Numbers
- Step 1: Consider the division \(\frac{5 + 6i}{1 - 2i}\).
- Step 2: Multiply the numerator and the denominator by the conjugate of the denominator: \((1 + 2i)\).
- Step 3: Expand both the numerator and the denominator:
- \(\frac{(5 + 6i)(1 + 2i)}{(1 - 2i)(1 + 2i)} = \frac{5 + 10i + 6i + 12i^2}{1 - 4i^2}\).
- Step 4: Simplify the terms: \(\frac{5 + 16i - 12}{1 + 4} = \frac{-7 + 16i}{5}\).
- Step 5: Write the result in standard form: \(-\frac{7}{5} + \frac{16}{5}i\).
- Answer: \(-\frac{7}{5} + \frac{16}{5}i\).
Video hướng dẫn cách tìm căn bậc hai của số âm, giải thích khái niệm và các bước thực hiện một cách dễ hiểu.
Cách Tìm Căn Bậc Hai của Số Âm
READ MORE:
Video hướng dẫn cách tìm căn bậc hai của số âm, giải thích khái niệm và quy trình thực hiện một cách dễ hiểu.
Tìm Căn Bậc Hai của Số Âm