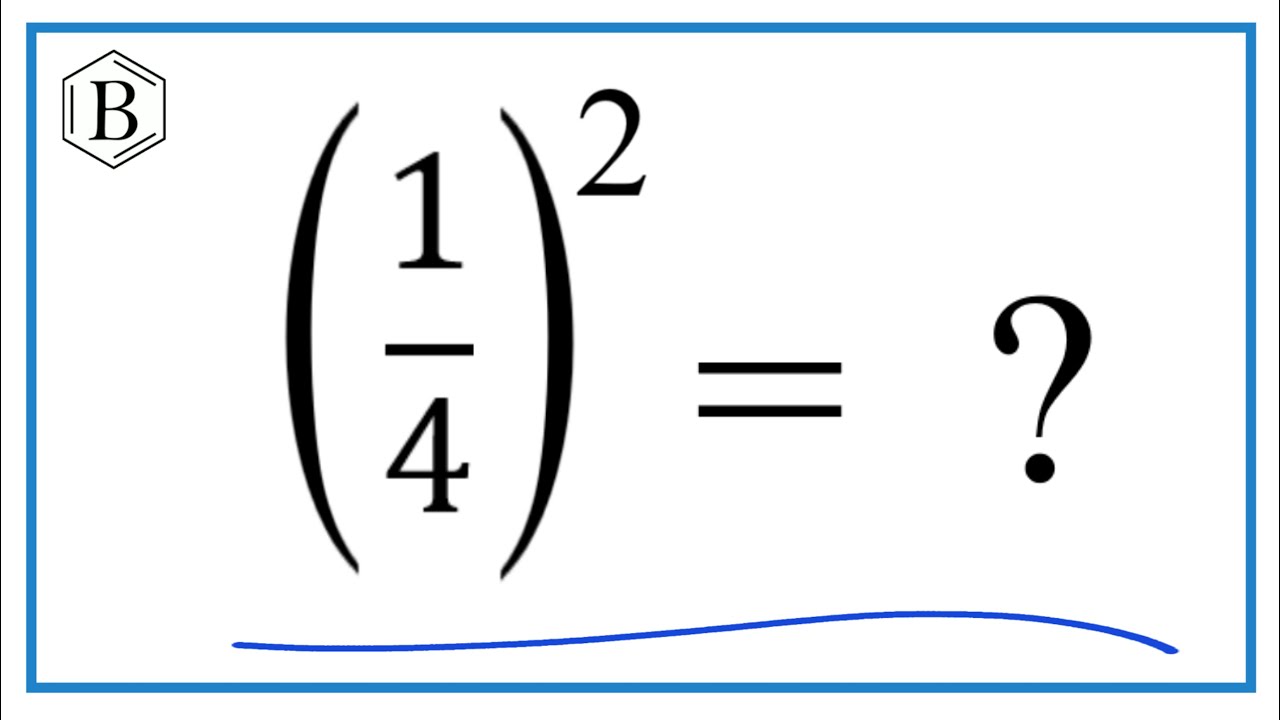Topic square root of 1/9: Discover the simplicity and significance of the square root of 1/9 in this comprehensive guide. We break down the concept, explain the calculation, and explore its practical applications. Whether you're a student or a math enthusiast, this article will enhance your understanding and appreciation of this fundamental mathematical concept.
Table of Content
- Simplifying the Square Root of 1/9
- Introduction to Square Roots
- Understanding Fractions and Their Square Roots
- Mathematical Explanation of the Square Root of 1/9
- Step-by-Step Calculation
- Visual Representation of the Square Root of 1/9
- Real-World Applications
- Common Misconceptions and Clarifications
- Practice Problems and Solutions
- Advanced Topics Related to Square Roots
- Conclusion
- Frequently Asked Questions (FAQs)
- YOUTUBE:
Simplifying the Square Root of 1/9
To simplify the square root of \( \frac{1}{9} \), we follow these steps:
- Rewrite the expression as a square root of a fraction: \( \sqrt{\frac{1}{9}} \).
- Use the property of square roots that allows us to separate the numerator and the denominator: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \).
- Apply this property to our expression: \( \sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} \).
- Calculate the square roots of the numerator and the denominator:
- The square root of 1 is 1: \( \sqrt{1} = 1 \).
- The square root of 9 is 3: \( \sqrt{9} = 3 \).
- Combine these results to get the simplified form: \( \frac{1}{3} \).
Exact and Decimal Forms
The exact form of the square root of \( \frac{1}{9} \) is \( \frac{1}{3} \). The decimal form is approximately 0.3333.
Using Online Calculators
Several online calculators can help you find the square root of \( \frac{1}{9} \) easily:
- provides step-by-step solutions for simplifying square roots.
- offers a simple calculator to input and find the square root.
- explains the properties and simplification of square roots in detail.
Video Explanation
For a visual explanation, you can watch this which demonstrates how to simplify the square root of \( \frac{1}{9} \).
| Form | Value |
|---|---|
| Exact Form | \( \frac{1}{3} \) |
| Decimal Form | 0.3333 |
By following these steps, you can simplify the square root of any fraction with ease.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because \(3 \times 3 = 9\).
In mathematical notation, the square root of a number \(x\) is written as \(\sqrt{x}\). For any non-negative number \(x\), \(\sqrt{x} \geq 0\).
Square roots can be applied to both whole numbers and fractions. Understanding square roots involves a few key points:
- Positive and Negative Roots: While the principal square root is non-negative, every positive number actually has two square roots: one positive and one negative. For instance, both 3 and -3 are square roots of 9.
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because they are squares of integers.
- Non-Perfect Squares: Numbers like 2, 3, 5, and 7 are not perfect squares, and their square roots are irrational numbers, meaning they cannot be expressed as exact fractions.
- Square Roots of Fractions: The square root of a fraction can be found by taking the square root of the numerator and the square root of the denominator separately. For example, \(\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3}\).
Let's consider the square root of 1/9:
\[
\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3}
\]
This demonstrates that the square root of 1/9 is 1/3. Understanding how to calculate and interpret square roots is crucial for solving various mathematical problems and real-world applications.
Understanding Fractions and Their Square Roots
Fractions represent parts of a whole and are written in the form \(\frac{a}{b}\), where \(a\) is the numerator and \(b\) is the denominator. Understanding the square roots of fractions involves taking the square root of both the numerator and the denominator separately.
Let's explore this step-by-step:
- Identify the Fraction: Consider the fraction \(\frac{1}{9}\).
- Square Root of the Numerator: Find the square root of the numerator (1).
- \(\sqrt{1} = 1\)
- Square Root of the Denominator: Find the square root of the denominator (9).
- \(\sqrt{9} = 3\)
- Combine the Results: Combine the square roots of the numerator and the denominator to find the square root of the fraction.
- \[ \sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3} \]
By following these steps, we see that the square root of \(\frac{1}{9}\) is \(\frac{1}{3}\). This method applies to any fraction, allowing us to break down the problem into more manageable parts.
To further illustrate this, consider another example:
Find the square root of \(\frac{4}{25}\):
\[
\sqrt{\frac{4}{25}} = \frac{\sqrt{4}}{\sqrt{25}} = \frac{2}{5}
\]
This shows that the square root of \(\frac{4}{25}\) is \(\frac{2}{5}\). By consistently applying these steps, you can determine the square root of any fraction.
Understanding fractions and their square roots is essential for various mathematical applications, from basic arithmetic to advanced algebra and beyond. This foundational knowledge enables us to tackle more complex problems with confidence and precision.
Mathematical Explanation of the Square Root of 1/9
The square root of a number is a value that, when multiplied by itself, gives the original number. To find the square root of a fraction, we need to consider both the numerator and the denominator separately. Let's take a closer look at the mathematical explanation of the square root of \(\frac{1}{9}\).
The fraction \(\frac{1}{9}\) consists of the numerator 1 and the denominator 9. The steps to find the square root are as follows:
- Identify the Fraction: We start with the fraction \(\frac{1}{9}\).
- Square Root of the Numerator: Calculate the square root of the numerator.
- \(\sqrt{1} = 1\)
- Square Root of the Denominator: Calculate the square root of the denominator.
- \(\sqrt{9} = 3\)
- Combine the Results: Combine the square roots of the numerator and the denominator to find the square root of the fraction.
- \[ \sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3} \]
To confirm our result, let's verify the calculation by squaring \(\frac{1}{3}\):
\[
\left( \frac{1}{3} \right)^2 = \frac{1^2}{3^2} = \frac{1}{9}
\]
This confirms that the square root of \(\frac{1}{9}\) is indeed \(\frac{1}{3}\).
Additionally, we can use the property of exponents to explain this. Recall that the square root of a number is the same as raising that number to the power of \(\frac{1}{2}\). Applying this to our fraction:
\[
\left( \frac{1}{9} \right)^{\frac{1}{2}} = \frac{1^{\frac{1}{2}}}{9^{\frac{1}{2}}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3}
\]
Understanding the mathematical principles behind finding the square root of a fraction, such as \(\frac{1}{9}\), provides a solid foundation for more complex mathematical concepts and problem-solving techniques.
Step-by-Step Calculation
Calculating the square root of a fraction involves finding the square root of both the numerator and the denominator separately. Let's go through the step-by-step process to find the square root of \(\frac{1}{9}\).
- Identify the Fraction: We begin with the fraction \(\frac{1}{9}\).
- Square Root of the Numerator: Calculate the square root of the numerator.
- \(\sqrt{1} = 1\)
- Square Root of the Denominator: Calculate the square root of the denominator.
- \(\sqrt{9} = 3\)
- Combine the Results: Combine the square roots of the numerator and the denominator.
- \[ \sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3} \]
For further clarity, let's validate our calculation by reversing the process:
- Square the Result: Square \(\frac{1}{3}\) to check if we get back the original fraction.
- \[ \left( \frac{1}{3} \right)^2 = \frac{1^2}{3^2} = \frac{1}{9} \]
- Verification: Since \(\frac{1}{9}\) is the original fraction, our calculation is correct.
This step-by-step method ensures accuracy and helps in understanding the process of finding the square root of a fraction. By following these steps, one can easily determine the square root of any given fraction.

Visual Representation of the Square Root of 1/9
Understanding the square root of a fraction can be enhanced through visual representation. Here, we will visualize the square root of \(\frac{1}{9}\) to gain a better comprehension of the concept.
Let's start with the fraction \(\frac{1}{9}\). Visually, this can be represented as one part out of nine equal parts. To find the square root, we consider the following steps:
- Square Root of the Numerator: The numerator is 1, and its square root is:
- \(\sqrt{1} = 1\)
- Square Root of the Denominator: The denominator is 9, and its square root is:
- \(\sqrt{9} = 3\)
The square root of the fraction is then:
\[
\sqrt{\frac{1}{9}} = \frac{1}{3}
\]
To visualize this, consider a square divided into 9 smaller squares (a 3x3 grid). One of these smaller squares represents \(\frac{1}{9}\) of the entire area.
When we take the square root of \(\frac{1}{9}\), we are looking for the side length of a smaller square that represents one part out of the nine equal parts. Each side of the smaller square will be:
\[
\frac{1}{3}
\]
Here is a table to illustrate this concept:
| \(\frac{1}{9}\) | ||||||||||||||
Each cell in the 3x3 grid represents \(\frac{1}{9}\) of the total area. The side length of each smaller square is \(\frac{1}{3}\), visually confirming that \(\sqrt{\frac{1}{9}} = \frac{1}{3}\).
This visual representation helps in understanding how the square root of a fraction operates in terms of area and length, providing a clearer picture of the mathematical process.
Real-World Applications
The concept of square roots, including the square root of \(\frac{1}{9}\), has various practical applications in real-world scenarios. Understanding these applications helps illustrate the importance and utility of square roots in everyday life and various fields. Here are some examples:
- Engineering and Construction:
- Engineers often use square roots in calculations involving areas and dimensions. For example, when determining the dimensions of materials, knowing the square root of specific measurements ensures accuracy.
- In construction, the square root of fractions can help in scaling models and converting measurements to achieve precise results.
- Finance and Economics:
- Square roots are used in financial formulas, such as calculating interest rates and understanding the variance in data sets. For instance, the square root of variances helps determine standard deviations, which are crucial in risk assessment.
- In economics, square roots can assist in understanding growth rates and the distribution of resources.
- Physics and Engineering:
- Square roots are essential in physics for calculating quantities like the root mean square speed in thermodynamics, which involves taking the square root of average velocities squared.
- In electrical engineering, the square root of power ratios helps in understanding decibel levels and signal strengths.
- Computer Science and Algorithm Design:
- Square roots are used in algorithms that involve geometric computations, such as calculating distances and optimizing search algorithms.
- Understanding square roots aids in graphics programming and simulations, where precise calculations are needed to render objects correctly.
- Everyday Life:
- Square roots appear in various day-to-day activities, such as determining the size of television screens (measured diagonally) or resizing images while maintaining proportions.
- Cooking and baking recipes often require scaling, where knowing the square root of proportions ensures accurate ingredient measurements.
These examples demonstrate that the square root of fractions like \(\frac{1}{9}\) is not just a theoretical concept but a practical tool used across numerous fields and everyday situations. Understanding how to calculate and apply square roots enables us to solve real-world problems with precision and confidence.
Common Misconceptions and Clarifications
Understanding the square root of fractions, such as \(\frac{1}{9}\), can sometimes lead to misconceptions. Here, we address some common misunderstandings and provide clarifications to ensure a solid grasp of the concept.
- Misconception: The Square Root of a Fraction is a Complex Calculation
Clarification: The process of finding the square root of a fraction is straightforward. It involves calculating the square root of the numerator and the denominator separately. For example:
\[
\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3}
\] - Misconception: Square Roots Only Apply to Whole Numbers
Clarification: Square roots can be applied to any positive number, including fractions and decimals. The principle remains the same regardless of the type of number. For instance, the square root of \(\frac{1}{9}\) is \(\frac{1}{3}\), just as the square root of 9 is 3.
- Misconception: The Square Root of a Fraction is Always Smaller Than the Original Fraction
Clarification: The square root of a fraction can be either smaller or larger than the original fraction, depending on the values involved. For \(\frac{1}{9}\), the square root \(\frac{1}{3}\) is larger than the original fraction. This is because:
\[
\frac{1}{3} \times \frac{1}{3} = \frac{1}{9}
\] - Misconception: Negative Numbers Cannot Have Real Square Roots
Clarification: While negative numbers do not have real square roots, we are focusing on positive fractions here. The concept of imaginary numbers addresses the square roots of negative numbers, but this is beyond the scope of simple fractions like \(\frac{1}{9}\).
- Misconception: The Process of Finding Square Roots is the Same for All Numbers
Clarification: The method to find square roots is consistent, but the ease of calculation varies. Perfect squares, like 1 and 9, have straightforward square roots (1 and 3, respectively). Non-perfect squares result in irrational numbers, which cannot be expressed as exact fractions.
By addressing these misconceptions, we can better understand the true nature of square roots, particularly for fractions like \(\frac{1}{9}\). Clear comprehension of these principles helps avoid errors and enhances mathematical problem-solving skills.
Practice Problems and Solutions
Practicing problems involving the square root of fractions helps reinforce understanding and improve problem-solving skills. Below are several practice problems along with step-by-step solutions.
Problem 1
Find the square root of \(\frac{4}{25}\).
- Step 1: Identify the fraction: \(\frac{4}{25}\).
- Step 2: Calculate the square root of the numerator:
- \(\sqrt{4} = 2\)
- Step 3: Calculate the square root of the denominator:
- \(\sqrt{25} = 5\)
- Step 4: Combine the results:
- \[ \sqrt{\frac{4}{25}} = \frac{\sqrt{4}}{\sqrt{25}} = \frac{2}{5} \]
Solution: The square root of \(\frac{4}{25}\) is \(\frac{2}{5}\).
Problem 2
Find the square root of \(\frac{16}{49}\).
- Step 1: Identify the fraction: \(\frac{16}{49}\).
- Step 2: Calculate the square root of the numerator:
- \(\sqrt{16} = 4\)
- Step 3: Calculate the square root of the denominator:
- \(\sqrt{49} = 7\)
- Step 4: Combine the results:
- \[ \sqrt{\frac{16}{49}} = \frac{\sqrt{16}}{\sqrt{49}} = \frac{4}{7} \]
Solution: The square root of \(\frac{16}{49}\) is \(\frac{4}{7}\).
Problem 3
Find the square root of \(\frac{1}{36}\).
- Step 1: Identify the fraction: \(\frac{1}{36}\).
- Step 2: Calculate the square root of the numerator:
- \(\sqrt{1} = 1\)
- Step 3: Calculate the square root of the denominator:
- \(\sqrt{36} = 6\)
- Step 4: Combine the results:
- \[ \sqrt{\frac{1}{36}} = \frac{\sqrt{1}}{\sqrt{36}} = \frac{1}{6} \]
Solution: The square root of \(\frac{1}{36}\) is \(\frac{1}{6}\).
Problem 4
Find the square root of \(\frac{9}{64}\).
- Step 1: Identify the fraction: \(\frac{9}{64}\).
- Step 2: Calculate the square root of the numerator:
- \(\sqrt{9} = 3\)
- Step 3: Calculate the square root of the denominator:
- \(\sqrt{64} = 8\)
- Step 4: Combine the results:
- \[ \sqrt{\frac{9}{64}} = \frac{\sqrt{9}}{\sqrt{64}} = \frac{3}{8} \]
Solution: The square root of \(\frac{9}{64}\) is \(\frac{3}{8}\).
Problem 5
Find the square root of \(\frac{25}{81}\).
- Step 1: Identify the fraction: \(\frac{25}{81}\).
- Step 2: Calculate the square root of the numerator:
- \(\sqrt{25} = 5\)
- Step 3: Calculate the square root of the denominator:
- \(\sqrt{81} = 9\)
- Step 4: Combine the results:
- \[ \sqrt{\frac{25}{81}} = \frac{\sqrt{25}}{\sqrt{81}} = \frac{5}{9} \]
Solution: The square root of \(\frac{25}{81}\) is \(\frac{5}{9}\).
By practicing these problems, you can develop a stronger understanding of how to find the square roots of fractions. This fundamental skill is essential for tackling more complex mathematical challenges.
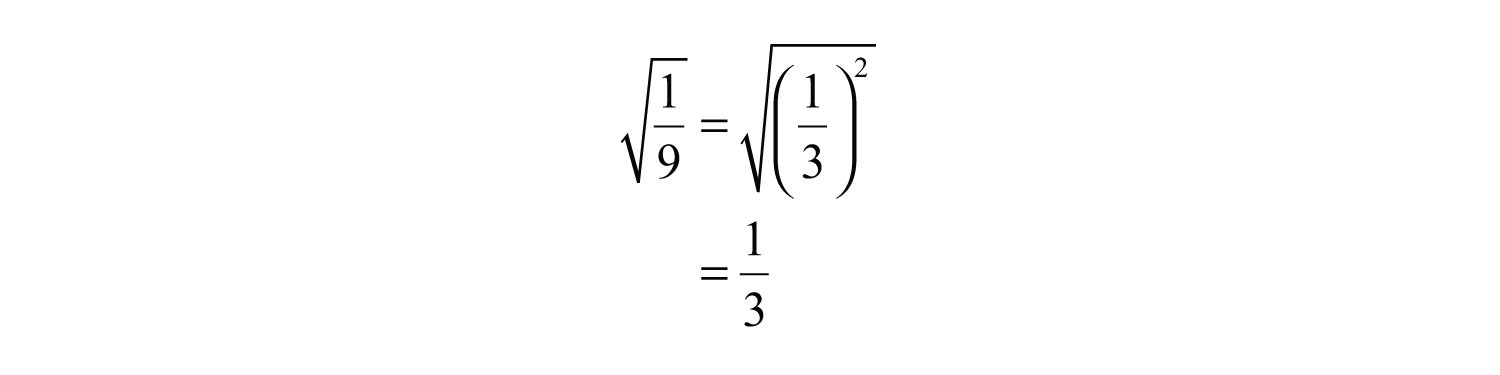
Advanced Topics Related to Square Roots
Understanding square roots goes beyond basic calculations, delving into advanced mathematical concepts and applications. This section explores various sophisticated topics related to square roots, providing a comprehensive understanding for those seeking deeper knowledge.
1. Irrational Numbers
While the square root of 1/9 is a rational number, many square roots are irrational. An irrational number cannot be expressed as a simple fraction. For example, the square root of 2 is an irrational number.
2. Complex Numbers
Square roots are not limited to positive numbers or fractions. The concept extends to negative numbers through the use of complex numbers. The square root of a negative number is defined as an imaginary number. For instance:
\[\sqrt{-1} = i\]
where \(i\) is the imaginary unit.
3. Square Roots in Different Number Systems
Square roots can be explored in various number systems, such as binary, octal, and hexadecimal. Calculating square roots in these systems follows different rules compared to the decimal system.
4. Algebraic Properties
- Product Property: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\)
- Quotient Property: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- Exponentiation: \(\sqrt{a^n} = a^{\frac{n}{2}}\)
5. Square Roots of Matrices
In linear algebra, the concept of square roots extends to matrices. A matrix \(A\) has a square root \(B\) if \(B \cdot B = A\). Finding the square root of a matrix is a complex process involving eigenvalues and eigenvectors.
6. Numerical Methods for Approximating Square Roots
There are several numerical methods to approximate square roots, especially for non-perfect squares. Some popular methods include:
- Newton's Method: An iterative method to approximate roots of a real-valued function.
- Babylonian Method: Also known as Heron's method, it involves an iterative averaging process.
7. Applications in Calculus
Square roots frequently appear in calculus, particularly in integrals and derivatives. For example, the derivative of the square root function is:
\[\frac{d}{dx} \sqrt{x} = \frac{1}{2\sqrt{x}}\]
8. Square Roots in Differential Equations
Square roots are used in solving differential equations. For instance, in second-order differential equations, characteristic equations often involve square roots to find solutions.
9. Quantum Mechanics
Square roots play a significant role in quantum mechanics, especially in the normalization of wave functions. The probability amplitude often involves square roots to ensure the total probability is one.
10. Square Roots in Geometry
In geometry, square roots are essential in various theorems and formulas, such as the distance formula between two points in a plane:
\[d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\]
By exploring these advanced topics, we gain a deeper appreciation of the wide-ranging applications and implications of square roots in mathematics and beyond.
Conclusion
The exploration of the square root of provides us with a clear understanding of how square roots interact with fractions and how to simplify them. Through the mathematical breakdown, we determined that:
- The square root of can be simplified by separating the numerator and the denominator under the square root, resulting in .
- Since equals 1 and equals 3, the simplified form is .
- The result in decimal form is approximately 0.333, reinforcing the concept that the square root of a fraction yields a simpler, often more intuitive, number.
In real-world applications, understanding how to simplify square roots, especially those of fractions, is vital in various fields such as engineering, physics, and even finance. The principles explored here extend beyond this specific example, providing a foundation for tackling more complex mathematical problems involving roots and fractions.
By demystifying these mathematical concepts, we can appreciate their simplicity and elegance, which are foundational to both basic and advanced mathematical studies.
Frequently Asked Questions (FAQs)
Below are some common questions and detailed answers regarding the square root of :
- What is the square root of ?
- How do you simplify ?
- Is the square root of a rational number?
- Can the square root of be negative?
- How is understanding the square root of a fraction useful?
The square root of is . This is because is 1 and is 3.
To simplify , you can separate the square root of the numerator and the denominator: . This simplifies to .
Yes, the square root of is a rational number because it can be expressed as a simple fraction .
While the principal (or non-negative) square root of is , there is also a negative square root, which is . Both values are valid solutions since squaring either will return .
Understanding the square root of fractions helps in various mathematical applications, such as simplifying expressions, solving equations, and understanding proportions in geometry and physics. It also builds a foundation for more advanced topics like calculus and complex numbers.
Căn Bậc Hai của 1/9 | Root(1/9)
READ MORE:
Rút gọn căn bậc hai của 1/9, căn bậc hai của 1/9