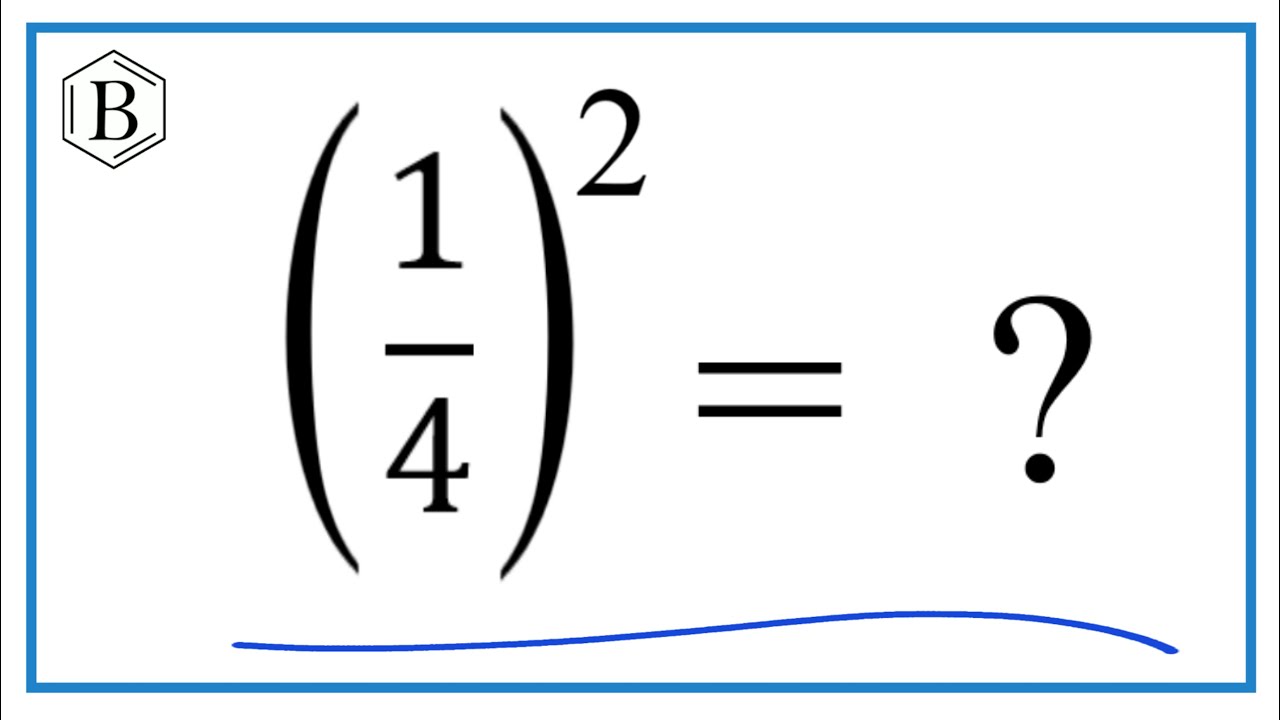Topic square root of 1/4 fraction: The square root of 1/4 is a fundamental concept in mathematics, providing a clear example of how to handle square roots of fractions. By breaking down the problem into simpler steps, anyone can understand the process and apply it to similar problems. This article will guide you through the steps of finding the square root of 1/4 with ease.
Table of Content
- Understanding the Square Root of 1/4
- Introduction to Square Roots
- Understanding Fractions and Their Properties
- Finding the Square Root of a Fraction
- Simplifying the Square Root of 1/4
- Applications of Square Roots in Fractions
- Common Mistakes and How to Avoid Them
- Practice Problems
- Further Reading and Resources
- YOUTUBE: Video hướng dẫn cách đơn giản hóa một phân số dưới căn bậc hai. Phép gian lận hợp pháp để giải các bài toán một cách nhanh chóng và chính xác.
Understanding the Square Root of 1/4
The square root of a fraction involves taking the square root of both the numerator and the denominator. Here's a detailed explanation using the example of 1/4:
Steps to Calculate the Square Root of 1/4
- Identify the numerator and denominator:
- Numerator: 1
- Denominator: 4
- Apply the square root to both the numerator and the denominator:
- √1 = 1
- √4 = 2
- Form the fraction with the results:
\[\sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2}\]
Alternative Explanation
The process can also be understood using the properties of exponents. The square root of a fraction \(\frac{a}{b}\) can be written as \(\frac{\sqrt{a}}{\sqrt{b}}\). In the case of \(\frac{1}{4}\), this becomes:
Therefore, the square root of 1/4 is 1/2.
Examples of Other Fractions
| Fraction | Square Root | Calculation |
|---|---|---|
| 9/16 | 3/4 | \(\sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4}\) |
| 1/25 | 1/5 | \(\sqrt{\frac{1}{25}} = \frac{\sqrt{1}}{\sqrt{25}} = \frac{1}{5}\) |
| 7/18 | ≈ 0.62 | \(\sqrt{\frac{7}{18}} = \frac{\sqrt{7}}{\sqrt{18}} ≈ 0.62\) (rounded to two decimal places) |
General Process for Finding the Square Root of a Fraction
- Simplify the fraction if possible.
- Find the square root of the numerator and denominator separately.
- Simplify the resulting fraction if necessary.
In some cases, fractions with irrational denominators may require rationalizing the denominator to simplify the square root.
Conclusion
Understanding how to find the square root of a fraction like 1/4 is a useful mathematical skill that can be applied to more complex fractions. The key steps involve simplifying the fraction, applying the square root to the numerator and denominator separately, and simplifying the result.

READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics that involves finding a number which, when multiplied by itself, equals the original number. The square root is denoted by the radical symbol (√).
For example, the square root of 9 is 3, because 3 multiplied by 3 equals 9:
\[ \sqrt{9} = 3 \]
Square roots can also apply to fractions. When dealing with fractions, the square root of the fraction is the square root of the numerator divided by the square root of the denominator:
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
Let's take the fraction \(\frac{1}{4}\) as an example. To find the square root of \(\frac{1}{4}\), we find the square root of 1 and the square root of 4 separately:
\[ \sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} \]
We know that \(\sqrt{1} = 1\) and \(\sqrt{4} = 2\), so:
\[ \sqrt{\frac{1}{4}} = \frac{1}{2} \]
This means the square root of \(\frac{1}{4}\) is \(\frac{1}{2}\).
Understanding square roots is crucial as they are widely used in various fields such as engineering, physics, and finance. They help in solving quadratic equations, understanding geometric shapes, and analyzing scientific data.
Understanding Fractions and Their Properties
Fractions represent a part of a whole and are composed of two parts: the numerator and the denominator. The numerator is the top number, indicating how many parts we have, while the denominator is the bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction \(\frac{1}{4}\), 1 is the numerator and 4 is the denominator. This fraction represents one part out of four equal parts.
Fractions have several important properties:
- Equivalent Fractions: Different fractions can represent the same value. For example, \(\frac{2}{4}\) is equivalent to \(\frac{1}{2}\) because both represent half of a whole.
- Simplifying Fractions: Fractions can often be simplified by dividing the numerator and the denominator by their greatest common divisor (GCD). For example, \(\frac{4}{8}\) can be simplified to \(\frac{1}{2}\) by dividing both 4 and 8 by 4.
- Improper Fractions and Mixed Numbers: An improper fraction has a numerator larger than or equal to the denominator (e.g., \(\frac{9}{4}\)). It can be converted into a mixed number, which combines a whole number with a fraction (e.g., \(2 \frac{1}{4}\)).
- Reciprocal of a Fraction: The reciprocal of a fraction is obtained by swapping its numerator and denominator. For example, the reciprocal of \(\frac{1}{4}\) is \(\frac{4}{1}\) or 4.
- Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. For example: \[ \frac{1}{4} + \frac{1}{4} = \frac{2}{4} = \frac{1}{2} \] \[ \frac{3}{4} - \frac{1}{4} = \frac{2}{4} = \frac{1}{2} \]
- Multiplying and Dividing Fractions: To multiply fractions, multiply the numerators and the denominators: \[ \frac{1}{4} \times \frac{1}{2} = \frac{1 \times 1}{4 \times 2} = \frac{1}{8} \] To divide fractions, multiply by the reciprocal of the divisor: \[ \frac{1}{4} \div \frac{1}{2} = \frac{1}{4} \times \frac{2}{1} = \frac{2}{4} = \frac{1}{2} \]
Understanding these properties is essential for working with fractions effectively in mathematics and various real-world applications.
Finding the Square Root of a Fraction
Finding the square root of a fraction involves determining a number which, when multiplied by itself, equals the original fraction. The process can be broken down into simple steps:
- Identify the Numerator and Denominator:
For the fraction \(\frac{1}{4}\), the numerator is 1 and the denominator is 4.
- Find the Square Root of the Numerator:
Determine the square root of the numerator. For \(\frac{1}{4}\), the numerator is 1, and \(\sqrt{1} = 1\).
- Find the Square Root of the Denominator:
Determine the square root of the denominator. For \(\frac{1}{4}\), the denominator is 4, and \(\sqrt{4} = 2\).
- Form the Fraction with the Square Roots:
Combine the square roots of the numerator and the denominator to form a new fraction:
\[ \sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2} \]
- Simplify if Necessary:
If the resulting fraction can be simplified further, do so. In this case, \(\frac{1}{2}\) is already in its simplest form.
Thus, the square root of \(\frac{1}{4}\) is \(\frac{1}{2}\).
This method can be applied to any fraction. By taking the square root of both the numerator and the denominator, you can find the square root of any fraction:
\[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
For instance, to find the square root of \(\frac{9}{16}\):
- The square root of the numerator (9) is 3.
- The square root of the denominator (16) is 4.
- Combine these results to get \(\frac{3}{4}\).
Therefore, \(\sqrt{\frac{9}{16}} = \frac{3}{4}\).
Understanding this process is essential for working with fractions in various mathematical contexts, including algebra and geometry.
Simplifying the Square Root of 1/4
Simplifying the square root of a fraction, such as \(\frac{1}{4}\), involves a few straightforward steps. Here is a detailed, step-by-step process:
- Understand the Fraction:
The fraction \(\frac{1}{4}\) means that the whole is divided into 4 equal parts, and we are considering 1 of those parts.
- Apply the Square Root to Both the Numerator and the Denominator:
To find the square root of \(\frac{1}{4}\), we take the square root of the numerator (1) and the square root of the denominator (4) separately:
\[ \sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} \]
- Calculate the Square Roots:
- The square root of 1 is 1, because \(1 \times 1 = 1\).
- The square root of 4 is 2, because \(2 \times 2 = 4\).
So we have:
\[ \sqrt{\frac{1}{4}} = \frac{1}{2} \]
- Verify the Result:
To ensure our result is correct, we can square \(\frac{1}{2}\) and check if it equals \(\frac{1}{4}\):
\[ \left( \frac{1}{2} \right)^2 = \frac{1^2}{2^2} = \frac{1}{4} \]
Since \(\frac{1}{2} \times \frac{1}{2} = \frac{1}{4}\), our simplified result is verified.
Thus, the square root of \(\frac{1}{4}\) is \(\frac{1}{2}\), and this fraction is in its simplest form. Understanding this simplification process helps in dealing with more complex fractions and in solving various mathematical problems efficiently.

Applications of Square Roots in Fractions
Square roots of fractions are used in various fields of mathematics, science, engineering, and everyday life. Here are some of the key applications:
- Geometry and Trigonometry:
Square roots are often used in geometry, especially in calculating distances and lengths. For example, in the Pythagorean theorem, the distance between two points in a coordinate plane is found using the square root of the sum of the squares of the differences in the coordinates:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
When working with fractional distances, square roots of fractions are essential.
- Physics and Engineering:
In physics, square roots of fractions appear in formulas involving wave speeds, energy, and other physical properties. For instance, the root mean square (RMS) value of an alternating current (AC) voltage or current involves the square root of the average of the squares of the values:
\[ V_{RMS} = \sqrt{\frac{1}{T} \int_0^T [V(t)]^2 \, dt} \]
- Probability and Statistics:
In probability and statistics, the standard deviation is calculated using the square root of the variance, which often involves fractional values:
\[ \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2} \]
Here, the variance is a fraction representing the average of the squared deviations from the mean.
- Finance:
In finance, the square root of fractions is used to calculate compound interest and to assess financial risk. For example, the standard deviation of investment returns, a measure of volatility, involves the square root of the variance.
- Biology and Medicine:
Square roots of fractions are used in various biological and medical calculations, such as determining concentrations and dosages. For example, the growth rate of a population or the spread of a disease might involve square roots.
- Everyday Life:
Square roots of fractions are encountered in daily activities such as cooking, where ingredient measurements may require adjustments based on scaling recipes up or down.
Understanding the applications of square roots in fractions helps in grasping how mathematical concepts are intertwined with practical problems in various disciplines and everyday situations.
Common Mistakes and How to Avoid Them
When working with the square root of fractions, students often encounter several common mistakes. Here, we will outline these mistakes and provide guidance on how to avoid them.
- Mistake 1: Incorrectly Simplifying the Fraction Before Finding the Square Root
Many students try to simplify the fraction
\(\frac{1}{4}\)before taking the square root, which can lead to errors.How to Avoid: Always take the square root of the numerator and the denominator separately. For example,
\(\sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2}\). - Mistake 2: Forgetting to Consider Both Positive and Negative Roots
Students often forget that square roots can have both positive and negative values.
How to Avoid: Remember that the square root function yields two values. For
\(\sqrt{\frac{1}{4}}\), the results are\(\frac{1}{2}\)and\(-\frac{1}{2}\). - Mistake 3: Misapplying Properties of Square Roots
Another common mistake is misapplying the properties of square roots, such as thinking
\(\sqrt{a+b} = \sqrt{a} + \sqrt{b}\), which is incorrect.How to Avoid: Understand and apply the correct property:
\(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).For\(\sqrt{\frac{1}{4}}\),the correct simplification is\(\frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2}\). - Mistake 4: Ignoring Simplification After Finding the Square Root
Some students do not simplify the result after finding the square root.
How to Avoid: Always check if the fraction can be simplified further. For instance, after finding
\(\sqrt{\frac{16}{64}}\),simplify the result to\(\frac{1}{2}\).
Practice Problems
To help you understand and master finding the square root of fractions, here are some practice problems. Work through each problem step by step, ensuring you follow the correct procedures and simplify your answers where possible.
- Problem 1: Find the square root of
\(\frac{9}{16}\).Solution:
- Take the square root of the numerator and the denominator separately:
\(\sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4}\) - So, the square root of
\(\frac{9}{16}\)is\(\frac{3}{4}\).
- Take the square root of the numerator and the denominator separately:
- Problem 2: Find the square root of
\(\frac{25}{100}\).Solution:
- Take the square root of the numerator and the denominator separately:
\(\sqrt{\frac{25}{100}} = \frac{\sqrt{25}}{\sqrt{100}} = \frac{5}{10}\) - Simplify the fraction:
\(\frac{5}{10} = \frac{1}{2}\) - So, the square root of
\(\frac{25}{100}\)is\(\frac{1}{2}\).
- Take the square root of the numerator and the denominator separately:
- Problem 3: Find the square root of
\(\frac{1}{36}\).Solution:
- Take the square root of the numerator and the denominator separately:
\(\sqrt{\frac{1}{36}} = \frac{\sqrt{1}}{\sqrt{36}} = \frac{1}{6}\) - So, the square root of
\(\frac{1}{36}\)is\(\frac{1}{6}\).
- Take the square root of the numerator and the denominator separately:
- Problem 4: Find the square root of
\(\frac{4}{49}\).Solution:
- Take the square root of the numerator and the denominator separately:
\(\sqrt{\frac{4}{49}} = \frac{\sqrt{4}}{\sqrt{49}} = \frac{2}{7}\) - So, the square root of
\(\frac{4}{49}\)is\(\frac{2}{7}\).
- Take the square root of the numerator and the denominator separately:
- Problem 5: Find the square root of
\(\frac{1}{9}\).Solution:
- Take the square root of the numerator and the denominator separately:
\(\sqrt{\frac{1}{9}} = \frac{\sqrt{1}}{\sqrt{9}} = \frac{1}{3}\) - So, the square root of
\(\frac{1}{9}\)is\(\frac{1}{3}\).
- Take the square root of the numerator and the denominator separately:
Further Reading and Resources
For those looking to delve deeper into the topic of square roots of fractions, the following resources provide a wealth of information and practice materials:
- Khan Academy: An extensive collection of video tutorials and practice exercises covering all aspects of square roots and fractions. .
- Virtual Nerd: Detailed tutorials on finding the square root of fractions, perfect for visual learners. .
- eTutorWorld: Personalized online tutoring and practice problems to strengthen your understanding of mathematical concepts, including the square roots of fractions. .
- Math is Fun: Clear explanations and interactive exercises to help simplify square roots and other fraction-related problems. .
- Edu2Know: Comprehensive articles that break down the process of finding square roots of fractions with practical examples and tips. .
These resources offer a mix of theoretical knowledge, practical exercises, and personalized help, making them invaluable tools for mastering the topic of square roots of fractions.

Video hướng dẫn cách đơn giản hóa một phân số dưới căn bậc hai. Phép gian lận hợp pháp để giải các bài toán một cách nhanh chóng và chính xác.
Đơn giản hóa một phân số dưới căn bậc hai - Phép gian lận hợp pháp trong toán học
READ MORE:
Video hướng dẫn cách lấy căn bậc hai của một phân số, ví dụ với căn(1/64). Học các bước chi tiết để hiểu rõ hơn về căn bậc hai của phân số.
Học cách lấy căn bậc hai của một phân số, căn(1/64)