Topic square root using division method: Discover the simplicity and effectiveness of the square root using division method. This comprehensive guide breaks down the process into easy-to-follow steps, making it accessible for anyone. Whether you're a student or just curious, learn how to master this traditional technique for accurate and quick square root calculations.
Table of Content
- Square Root Calculation Using Division Method
- Introduction to the Division Method for Square Roots
- Steps to Calculate Square Root Using the Division Method
- Detailed Example of Square Root Calculation
- Mathematical Foundation of the Division Method
- Advantages of Using the Division Method
- Limitations and Considerations
- Practical Applications of the Division Method
- Alternative Methods for Finding Square Roots
- Common Mistakes and How to Avoid Them
- Historical Background of the Division Method
- Advanced Techniques and Tips
- Frequently Asked Questions
- Conclusion
- YOUTUBE: Hướng dẫn cách tìm căn bậc hai của các số lớn bằng phương pháp chia, dễ hiểu và chi tiết cho người học.
Square Root Calculation Using Division Method
The division method, also known as the long division method, is a manual technique to find the square root of a number. This method involves a step-by-step process similar to long division, and it can be particularly useful for finding square roots of numbers that are not perfect squares. Below is a detailed guide on how to perform this method.
Steps to Calculate Square Root Using Division Method
-
Pair the Digits: Starting from the decimal point, pair the digits of the number in groups of two. If the number is whole, start from the unit place and move left. If it is a decimal, pair the digits on the right of the decimal point.
-
Find the Largest Number: Find the largest number whose square is less than or equal to the first pair or single digit. This number becomes the first digit of the square root.
-
Subtract and Bring Down: Subtract the square of the first digit from the first pair or single digit and bring down the next pair of digits next to the remainder.
-
Form the Divisor: Double the current result and form a new divisor by appending a digit that will give a product less than or equal to the current dividend when multiplied by the new divisor.
-
Repeat: Repeat the steps of subtracting, bringing down the next pair, forming a new divisor, and finding the next digit until you have processed all digit pairs of the number.
Example
Let's find the square root of 2025 using the division method:
-
Pair the digits: 20 | 25
-
Find the largest number whose square is ≤ 20. That number is 4 (since \(4^2 = 16\)).
-
Subtract and bring down the next pair: \(20 - 16 = 4\), then bring down 25, making it 425.
-
Double the current quotient (4), which gives 8. Find a digit X such that \(8X \times X \leq 425\). The digit is 5 (since \(85 \times 5 = 425\)).
-
Thus, the square root of 2025 is 45.
Mathematical Representation
The steps can be represented mathematically as:
Using MathJax:
\[
\sqrt{2025} = 45
\]
The long division method helps in breaking down the process into manageable steps, making it easier to understand and compute the square root manually.

READ MORE:
Introduction to the Division Method for Square Roots
The division method, also known as the long division method, is a manual technique for finding the square root of a number. This traditional approach, akin to the long division process, is especially useful for numbers that are not perfect squares. By following a structured, step-by-step process, you can determine the square root with precision.
Here’s a detailed guide on how to perform the division method for square roots:
-
Pair the Digits: Begin by pairing the digits of the number from right to left. For whole numbers, start from the decimal point moving left. For decimal numbers, pair the digits on both sides of the decimal point.
-
Initial Estimation: Find the largest number whose square is less than or equal to the first pair of digits (or the first single digit if there are no pairs). This number will be the first digit of the square root.
-
Set Up for Division: Subtract the square of the first digit from the first pair (or single digit) and bring down the next pair of digits to the right of the remainder, forming a new dividend.
-
Forming the Divisor: Double the current result of the square root and determine a new divisor by appending a digit to this doubled number. The digit should be such that when the new divisor is multiplied by this digit, the product is less than or equal to the new dividend.
-
Calculate and Repeat: Subtract the product from the new dividend, bring down the next pair of digits, and repeat the process until all digit pairs have been used. Continue the process until you achieve the desired precision.
By following these steps, you can manually calculate the square root of any given number using the division method, making it a valuable skill for mathematical problem-solving.
Steps to Calculate Square Root Using the Division Method
The division method, also known as the long division method, allows for a precise and manual calculation of square roots. Here is a detailed, step-by-step guide on how to use this method:
-
Pair the Digits: Start by pairing the digits of the number from right to left. For whole numbers, create pairs starting from the decimal point and moving left. For decimal numbers, pair the digits on both sides of the decimal point. For example, to find the square root of 1521, pair it as 15 | 21.
-
Initial Estimation: Find the largest number whose square is less than or equal to the first pair (or single digit if there is no pair). This number will be the first digit of the square root. In our example, the largest number whose square is ≤ 15 is 3, because \(3^2 = 9\).
-
Set Up for Division: Subtract the square of the first digit from the first pair (or single digit) and write the remainder. Bring down the next pair of digits next to the remainder to form a new dividend. Here, \(15 - 9 = 6\), and bring down 21 to get 621.
-
Form the New Divisor: Double the current quotient (first digit of the square root) to get a new divisor. Append a digit to this doubled number such that when multiplied by this new digit, the product is less than or equal to the new dividend. For the current quotient of 3, doubling gives 6. We need to find a digit X such that \(6X \times X \leq 621\). The digit is 1, because \(61 \times 1 = 61\).
-
Subtract and Repeat: Subtract the product from the new dividend, write the remainder, and bring down the next pair of digits. Repeat the process until all digit pairs have been processed. Here, \(621 - 61 = 560\), and we bring down the next pair. If there are no more digits, append zeros to continue the calculation for more precision.
Following these steps systematically ensures an accurate calculation of the square root using the division method. This method is particularly useful for manual calculations where a calculator is not available.
Detailed Example of Square Root Calculation
To understand the long division method for calculating square roots, let's walk through a detailed example of finding the square root of 529 step by step.
-
Pair the Digits:
Start by pairing the digits of the number from right to left. For 529, we have the pairs: 5 | 29.
-
Find the Largest Number:
Find the largest number whose square is less than or equal to the first pair (5). The largest such number is 2, because 22 = 4.
-
Set Up the Initial Division:
Write 2 as the first digit of the square root. Subtract 4 (22) from 5, giving a remainder of 1. Bring down the next pair (29) to make the new dividend 129.
2 4 -- 1 29 -
Double the Quotient and Find the Next Digit:
Double the current quotient (2), giving 4. Now, find a digit X such that 4X multiplied by X is less than or equal to 129. The digit is 3 because 43 * 3 = 129.
-
Complete the Division:
Write 3 as the next digit of the quotient, making it 23. Subtract 129 from 129, giving a remainder of 0. Since there are no more digits to bring down, the process is complete.
23 4 -- 129 129 --- 0
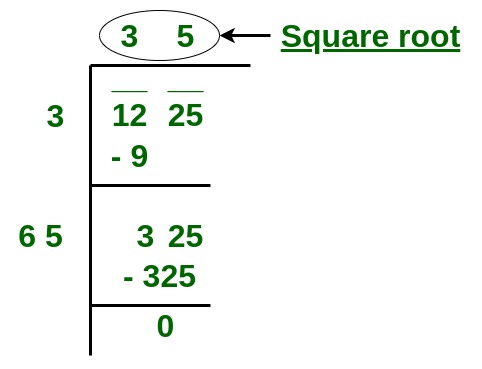
Therefore, the square root of 529 is 23.
Let's also see an example with a non-perfect square, 68.
-
Pair the Digits:
Pair the digits from right to left: 68.
-
Find the Largest Number:
The largest number whose square is less than or equal to 6 is 2 (22 = 4).
-
Set Up the Initial Division:
Write 2 as the first digit of the square root. Subtract 4 from 6, giving a remainder of 2. Bring down the next pair (8) to make the new dividend 28.
2 4 -- 28 -
Double the Quotient and Find the Next Digit:
Double the current quotient (2), giving 4. Now, find a digit X such that 4X multiplied by X is less than or equal to 28. The digit is 6 because 46 * 6 = 276 (closest to 280 without exceeding it).
-
Complete the Division:
Write 6 as the next digit of the quotient, making it 26. Continue the process to find more decimal places if needed. Here, for simplicity, we'll stop.
26 4 -- 28 28 --- 0
Therefore, the square root of 68 is approximately 8.246.
Mathematical Foundation of the Division Method
The division method for finding square roots is a systematic approach based on the principles of long division and involves several steps to obtain the square root of a given number, whether it is a perfect square or not. This method is particularly useful for manual calculations without the need for a calculator.
Here's a step-by-step explanation of the mathematical foundation underlying this method:
-
Preparation: Begin by pairing the digits of the number from the decimal point. For whole numbers, pair the digits from right to left. For decimal numbers, pair the digits from left to right and from right to left after the decimal point. For example, for 152.2756, the pairs would be (01)(52).(27)(56).
-
Initial Setup: Determine the largest integer whose square is less than or equal to the first pair. This number will be the first digit of the square root. Subtract the square of this number from the first pair and bring down the next pair to the right of the remainder. For instance, if we are finding the square root of 152, we start with 1, since 1^2 = 1 and 1 is the largest square less than or equal to 01.
-
Division Step: Double the current quotient and write it as the new divisor. Find a digit, let's call it D, such that when you append it to the new divisor and multiply by D, the product is less than or equal to the current dividend. For example, if our current quotient is 1, we double it to get 2, and then we try to find a digit D such that (20 + D) * D is less than or equal to the new dividend.
-
Subtract and Repeat: Subtract the product from the current dividend and bring down the next pair of digits. Repeat the process: double the current quotient, append a suitable digit to the divisor, find a new digit D, multiply, subtract, and bring down the next pair until all pairs have been processed.
This method leverages the properties of squares and the systematic approach of division to break down the calculation into manageable steps. The long division method is particularly useful for its simplicity and accuracy, especially before the advent of modern calculators.
To summarize, the division method for finding square roots involves pairing digits, iterative division, doubling the quotient, and carefully selecting digits to build the square root step by step.
Advantages of Using the Division Method
The division method for finding square roots offers several advantages, making it a valuable tool for both educational and practical applications. Here are some key benefits:
- Accuracy: The division method allows for precise calculation of square roots, especially useful for non-perfect squares where exact values are needed. This method can be extended to achieve the desired level of accuracy by continuing the division process.
- Understanding: By using the division method, learners can gain a deeper understanding of the square root concept and the relationship between numbers. This method reinforces basic arithmetic skills and enhances number sense.
- Simplicity: Once the steps are mastered, the division method is straightforward and systematic. It involves simple arithmetic operations (division, multiplication, and subtraction) that are easy to follow and execute.
- Versatility: This method can be applied to both whole numbers and decimals, making it versatile for various mathematical problems. It can also be used to find the square roots of large numbers without the need for a calculator.
- Foundational Knowledge: Learning the division method provides a strong foundation for more advanced mathematical concepts. It serves as a stepping stone to understanding algorithms and iterative methods used in higher-level mathematics.
- Problem Solving: The method enhances problem-solving skills by encouraging logical thinking and step-by-step analysis. It helps students develop a structured approach to tackling mathematical problems.
- Historical Relevance: The division method has historical significance as one of the earliest algorithms used for finding square roots. Understanding its historical context can provide insight into the development of mathematical techniques over time.
- Real-world Applications: Knowledge of the division method can be applied in various fields such as engineering, physics, and finance where precise calculations of square roots are required. This practical application underscores its importance beyond the classroom.
In conclusion, the division method for finding square roots is not only an effective mathematical tool but also a valuable educational resource that fosters a deeper understanding of numerical relationships and enhances problem-solving abilities.
Limitations and Considerations
The division method for finding square roots, while systematic and reliable, has certain limitations and considerations that users should be aware of:
- Complexity for Large Numbers: The division method can become quite cumbersome when dealing with very large numbers. As the number of digits increases, the process involves more steps, making it more time-consuming and prone to errors.
- Non-Perfect Squares: For numbers that are not perfect squares, the division method does not provide an exact integer result. Instead, it yields a decimal approximation, which may require rounding based on the desired precision.
- Decimal and Fractional Numbers: Calculating the square root of decimal or fractional numbers using the division method can be more complex, requiring careful placement of the decimal point and pairing of digits. This adds to the difficulty, especially for beginners.
- Manual Calculation Errors: The method involves multiple steps of division, multiplication, and subtraction. Each step must be performed accurately, and any small error can propagate through the process, leading to incorrect results.
- Learning Curve: Mastering the division method requires understanding and practice. It is not as intuitive as other methods like estimation or using a calculator, and beginners might find it challenging to grasp initially.
- Time-Consuming: Compared to using a calculator or digital tools, the division method is significantly slower. For quick calculations, especially in practical applications, other methods are often preferred.
- Use of Approximation: When dealing with irrational numbers, the division method only provides an approximation of the square root. The level of precision depends on how many decimal places are calculated, which may not always meet the requirements for certain applications.
- Limited Practicality for Complex Problems: In cases involving very large or very small numbers, or when high precision is needed, the division method might not be practical compared to modern computational tools.
Despite these limitations, the division method remains a valuable educational tool. It provides a deeper understanding of the concept of square roots and enhances numerical skills through its step-by-step approach. For historical and theoretical contexts, it showcases the evolution of mathematical methods and the foundational techniques used before the advent of calculators.
Practical Applications of the Division Method
The division method for finding square roots is a valuable mathematical technique with various practical applications. Below are some of the key areas where this method is particularly useful:
- Engineering and Architecture: Accurate calculation of square roots is crucial in engineering and architectural design, especially when dealing with areas, volumes, and other geometric properties.
- Financial Calculations: In finance, square roots are often used in the calculation of compound interest, standard deviations in statistics, and various algorithms for option pricing models.
- Physics and Chemistry: The division method aids in solving equations involving square roots, which appear frequently in formulas for wave functions, kinetic energy, and other physical properties.
- Computer Graphics: Calculations involving square roots are fundamental in computer graphics for operations like distance calculations, normalization of vectors, and rendering algorithms.
- Education: Teaching the division method helps students understand the concept of square roots deeply and enhances their problem-solving skills.
- Everyday Problem Solving: From calculating dimensions for home projects to determining the correct size for a television screen, knowing how to find square roots manually can be very practical.
To illustrate the practical application of the division method, let's consider an example where we need to calculate the square root of a number in an engineering context:
- Suppose we need to find the square root of 2025, which is part of a calculation for determining a structural load.
- Using the division method:
- Pair the digits from right to left: (20)(25).
- Find the largest number whose square is less than or equal to 20, which is 4 (since 42 = 16).
- Subtract the square from the first pair: 20 - 16 = 4. Bring down the next pair to get 425.
- Double the quotient (4) to get 8. Determine the next digit (5) such that 85 * 5 is less than or equal to 425.
- Perform the multiplication and subtraction: 425 - 425 = 0.
- The quotient (45) is the square root of 2025.
Thus, by using the division method, we accurately find that the square root of 2025 is 45. This step-by-step approach demonstrates the method's utility in providing precise results necessary for practical applications in various fields.
Alternative Methods for Finding Square Roots
While the division method is a reliable way to find square roots, there are several other methods available that can be more efficient or convenient depending on the context. Here are some of the alternative methods:
- Prime Factorization Method
This method involves breaking down the number into its prime factors and then pairing the prime factors to find the square root.
- Factorize the number into its prime factors.
- Pair the prime factors.
- Multiply one factor from each pair to get the square root.
For example, to find the square root of 144:
\[144 = 2^4 \times 3^2\]
Taking the square root, we pair the factors: \[\sqrt{144} = \sqrt{(2^2)^2 \times (3)^2} = 2^2 \times 3 = 12\]
- Newton's Method (Newton-Raphson Method)
This iterative method is based on calculus and provides a successive approximation to the square root. It is especially useful for finding square roots of non-perfect squares.
- Start with an initial guess \(x_0\).
- Use the formula \(x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right)\), where \(S\) is the number whose square root is to be found.
- Repeat the process until the desired accuracy is achieved.
For example, to find \(\sqrt{10}\):
Initial guess \(x_0 = 3\)
Iteration 1: \[x_1 = \frac{1}{2} \left( 3 + \frac{10}{3} \right) = 3.1667\]
Iteration 2: \[x_2 = \frac{1}{2} \left( 3.1667 + \frac{10}{3.1667} \right) = 3.1623\]
Continuing this process yields a more accurate value for \(\sqrt{10}\).
- Babylonian Method (Hero's Method)
This ancient method is similar to Newton's method and involves averaging guesses to get closer to the square root.
- Start with an initial guess \(x_0\).
- Use the formula \(x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right)\), where \(S\) is the number.
- Repeat until convergence.
This method is particularly simple and effective for manual calculations.
- Exponential and Logarithm Method
This method uses the properties of exponents and logarithms to find the square root.
- Express the square root in terms of exponentials: \(\sqrt{S} = S^{1/2}\).
- Use logarithms to simplify: \[\log(\sqrt{S}) = \frac{1}{2} \log(S)\].
- Find the antilog to get the square root.
For example, to find \(\sqrt{16}\):
\[\sqrt{16} = 16^{1/2} = 10^{(\log_{10}(16)/2)} = 10^{0.60206} = 4\]
- Using Calculators and Computers
Modern calculators and computer software can quickly and accurately find square roots using built-in functions. This method is the most convenient for complex or large numbers.
Each of these methods has its own advantages and applications. The choice of method depends on the context, the available tools, and the desired accuracy.

Common Mistakes and How to Avoid Them
Calculating square roots using the division method can be precise, but there are common mistakes that learners often make. Here are some of these mistakes and tips on how to avoid them:
- Incorrect Pairing of Digits:
When setting up the problem, it is crucial to correctly pair the digits starting from the decimal point and moving both left and right. An incorrect pairing can lead to significant errors in the calculation.
Tip: Always double-check the grouping of digits. For example, for the number 1234.567, the pairs should be (12)(34).(56)(70).
- Misplacement of the Decimal Point:
A common error is misplacing the decimal point during the division process, which leads to incorrect results.
Tip: Ensure the decimal point is correctly positioned after each step. If necessary, write the decimal point in all intermediary steps to keep track.
- Incorrect Subtraction:
Subtraction mistakes can happen frequently, especially in the iterative steps of the division method.
Tip: Perform the subtraction carefully and double-check each step before moving on to the next iteration.
- Choosing the Wrong Quotient:
Selecting an incorrect quotient can derail the entire process, leading to inaccurate results.
Tip: Choose the largest possible digit for the quotient that, when squared, is less than or equal to the current number. Test different digits if unsure.
- Forgetting to Double the Quotient:
During the steps where you find the new divisor, forgetting to double the current quotient can lead to errors.
Tip: Always remember to double the quotient from the previous step before determining the new digit for the quotient.
- Incorrect Placement of Zero Pairs:
When the decimal part of the number comes into play, it is easy to misplace the zero pairs, affecting the accuracy of the final result.
Tip: Add pairs of zeros correctly after placing the decimal point, and ensure the pairs are aligned properly during the calculation.
By being aware of these common mistakes and following these tips, the accuracy of calculating square roots using the division method can be significantly improved.
Historical Background of the Division Method
The division method for finding square roots, also known as the long division method or the digit-by-digit method, has its roots in ancient mathematics. This technique was developed as a systematic approach to finding square roots before the advent of modern calculators and computers.
Historically, the method can be traced back to ancient Babylonian and Greek mathematicians. These early scholars sought ways to simplify complex arithmetic operations and devised various algorithms to achieve accurate results.
The division method became more formalized during the Renaissance period. European mathematicians like Leonardo of Pisa (known as Fibonacci) played a significant role in disseminating mathematical knowledge, including methods for extracting square roots.
The method was widely taught in schools and used for practical computations. It involved a step-by-step process that allowed mathematicians and students to manually find square roots with a high degree of precision.
Over time, the division method was refined and incorporated into mathematical textbooks. It remained a fundamental part of arithmetic education well into the 20th century.
With the rise of electronic calculators and digital computers, the manual use of the division method has declined. However, understanding this historical technique provides valuable insights into the evolution of mathematical computation and the ingenuity of early mathematicians.
Advanced Techniques and Tips
To master the division method for finding square roots, it’s crucial to understand and apply advanced techniques that can streamline the process and improve accuracy. Here are some tips and methods:
Efficient Pairing and Decimal Handling
When dealing with both whole numbers and decimals, ensure to correctly pair the digits:
- For whole numbers, start pairing from the unit place towards the left.
- For decimal numbers, start pairing from the decimal point towards the right.
Doubling and Adjusting Divisors
After finding the initial divisor, remember to double it before selecting the next digit for the quotient:
- Double the current quotient.
- Add a placeholder for the new digit.
- Select the highest digit that keeps the product less than or equal to the current dividend.
Using Estimation and Validation
Estimation can help guide your process and verify your results:
- Estimate the square root to get a rough idea of the answer.
- After computing, multiply the quotient by itself to ensure it approximates the original number.
Shortcut Techniques
With practice, certain shortcuts and patterns can be recognized:
- Memorize common square roots and their approximations for quicker calculations.
- Use patterns in divisors and quotients to anticipate the next steps.
Practice Problems
Regular practice with different numbers helps in mastering the method. Here are some practice problems:
- Find the square root of 529.
- Calculate the square root of 10404 using the division method.
- Determine the square root of 0.000729.
Organizational Tips
Maintaining a clear workspace and organized calculations can minimize errors:
- Keep digits neatly aligned during calculations.
- Use a systematic approach to bring down pairs of digits and handle remainders.
Understanding the Theory
Deepening your understanding of why the division method works can enhance your proficiency:
- Study the mathematical principles behind the long division method for square roots.
- Understand how the method iteratively narrows down the square root by refining estimates.
By applying these advanced techniques and regularly practicing, you can become proficient in the division method for finding square roots, making the process both faster and more accurate.
Frequently Asked Questions
1. What are the major steps to find the square root by the long division method?
The long division method for finding square roots involves five main steps:
- Divide: Group the digits in pairs from right to left. Find the largest number whose square is less than or equal to the first group. This number is the first digit of the root.
- Multiply: Multiply the divisor by the quotient and write the result below the first group.
- Subtract: Subtract the result from the first group.
- Bring Down: Bring down the next pair of digits next to the remainder to form a new dividend.
- Repeat: Repeat the process until all the digits have been brought down.
2. How does the long division method work to find square roots?
The long division method works by repeatedly dividing, multiplying, and subtracting in a manner similar to traditional long division, but it focuses on pairs of digits. Each step narrows down the possible digits of the square root by ensuring the divisor, when multiplied by itself, is less than or equal to the current dividend.
3. How can we find the square root of a decimal number by the division method?
To find the square root of a decimal number using the long division method:
- Pair the digits of the number starting from the decimal point and moving both left and right.
- Apply the long division method as with whole numbers, treating pairs of digits as you bring them down.
- If necessary, append zeros to the end of the decimal to ensure all pairs are complete.
4. What are the symbols for division?
The symbols used for division include:
- The division sign (÷)
- The slash (/)
- The horizontal line (_)
5. What are the three ways to divide?
The three common ways to represent division are:
- Using the division sign (e.g., 8 ÷ 2)
- Using the slash (e.g., 8/2)
- Using the horizontal line in a long division tableau
6. What are the five steps of long division?
The five steps of long division are:
- Divide
- Multiply
- Subtract
- Bring down
- Repeat
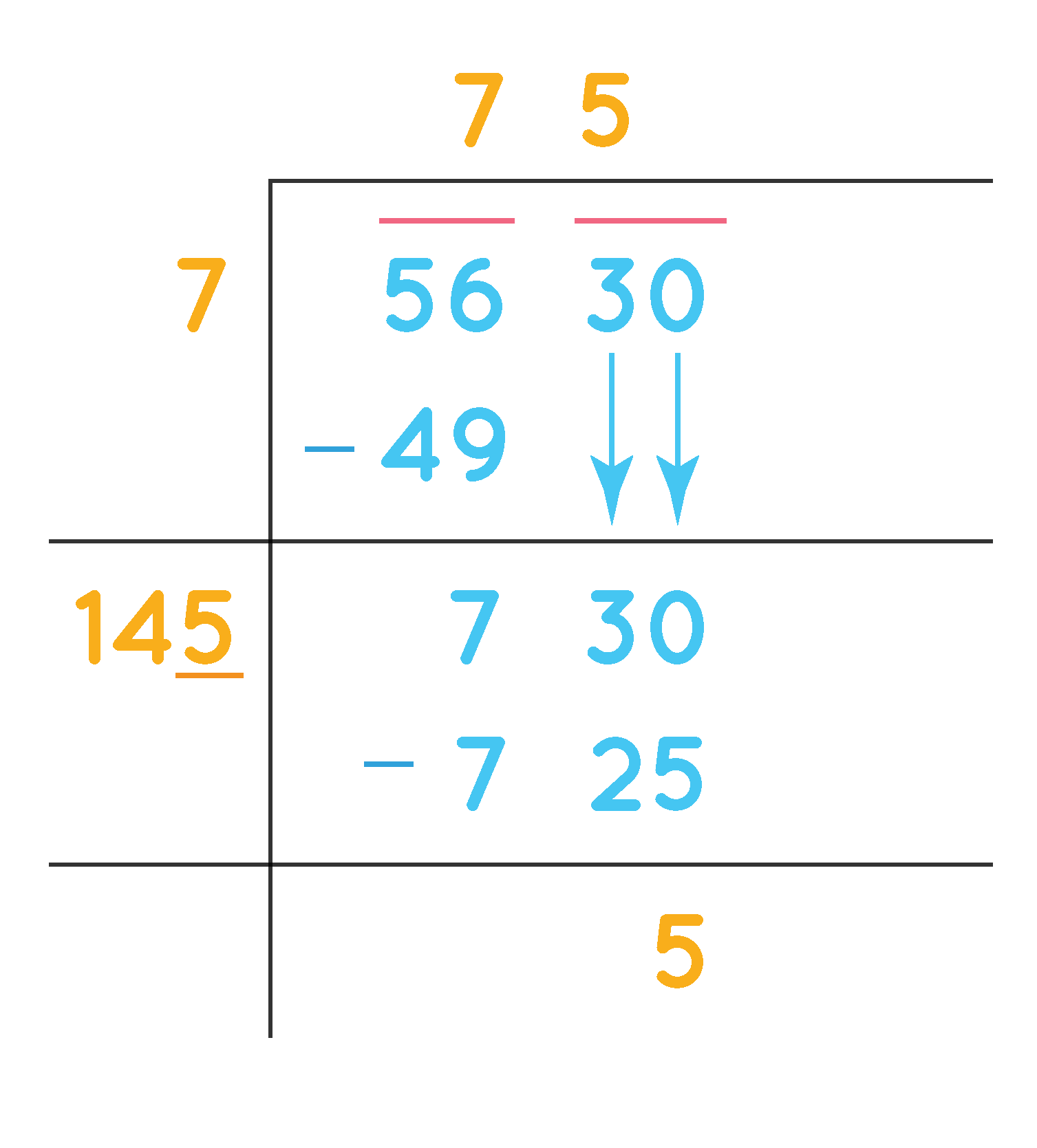
Conclusion
The division method for finding square roots is a powerful and reliable mathematical technique. It allows for the precise calculation of square roots, particularly for non-perfect squares, and provides a systematic approach that can be easily followed and understood. Through a series of well-defined steps, this method breaks down complex calculations into manageable parts, ensuring accuracy and clarity.
One of the key advantages of the division method is its ability to handle large numbers and decimals with equal efficiency. By grouping digits and performing iterative calculations, the method progressively refines the result, offering an exact value up to the desired decimal places. This makes it particularly useful in various practical applications, from engineering to finance, where precise numerical values are essential.
Moreover, the division method reinforces fundamental arithmetic skills and enhances number sense. As students and practitioners work through the steps, they gain a deeper understanding of the relationships between numbers and the properties of square roots. This foundational knowledge is invaluable for tackling more advanced mathematical concepts and problems.
However, it's important to acknowledge the method's limitations. The division method can be time-consuming and may require significant practice to master. Additionally, for very large numbers or highly precise calculations, computational tools or algorithms may offer more efficiency. Despite these considerations, the division method remains a cornerstone of mathematical education and practice, providing a robust framework for understanding and calculating square roots.
In conclusion, the division method for square roots is a versatile and educational tool. Its step-by-step approach not only delivers accurate results but also enriches the learner's mathematical experience. By practicing this method, individuals can enhance their problem-solving skills and build a solid foundation for future mathematical endeavors.
Hướng dẫn cách tìm căn bậc hai của các số lớn bằng phương pháp chia, dễ hiểu và chi tiết cho người học.
Làm Thế Nào Để Tìm Căn Bậc Hai Của Các Số Lớn Bằng Phương Pháp Chia
READ MORE:
Hướng dẫn chi tiết cách tìm căn bậc hai của một số bằng phương pháp chia dài, phần 1, từ Infinity Learn.
Căn Bậc Hai Của Một Số Bằng Phương Pháp Chia Dài - Phần 1 | Số Mũ | Infinity Learn