Topic square root 76: Discover everything you need to know about the square root of 76. This comprehensive guide covers basic concepts, mathematical representations, calculation methods, and real-world applications. Whether you're a student or a math enthusiast, you'll find valuable insights and practical tips for understanding and using the square root of 76.
Table of Content
- Square Root of 76
- Introduction
- Definition and Basic Concepts
- Mathematical Representation
- Methods to Calculate Square Root
- Using Calculators and Computers
- Excel and Google Sheets Functions
- Approximation and Rounding
- Applications in Geometry
- Real-World Examples
- Rational vs Irrational Numbers
- Perfect Squares and Imperfect Squares
- Common Questions and FAQs
- YOUTUBE: Video hướng dẫn cách đơn giản hóa căn bậc hai của 76. Học cách tính toán sqrt(76) một cách dễ dàng và chính xác.
Square Root of 76
The square root of 76 is a number that, when multiplied by itself, equals 76. Mathematically, this can be represented as:
\(\sqrt{76} = 8.717797887\) (approximately 8.718)
Simplified Radical Form
The square root of 76 can be simplified by expressing it in terms of its factors:
\(\sqrt{76} = \sqrt{2 \times 38} = \sqrt{2 \times 2 \times 19} = 2\sqrt{19}\)
Decimal Form
In decimal form, the square root of 76 is approximately:
\(\sqrt{76} \approx 8.717797887\)
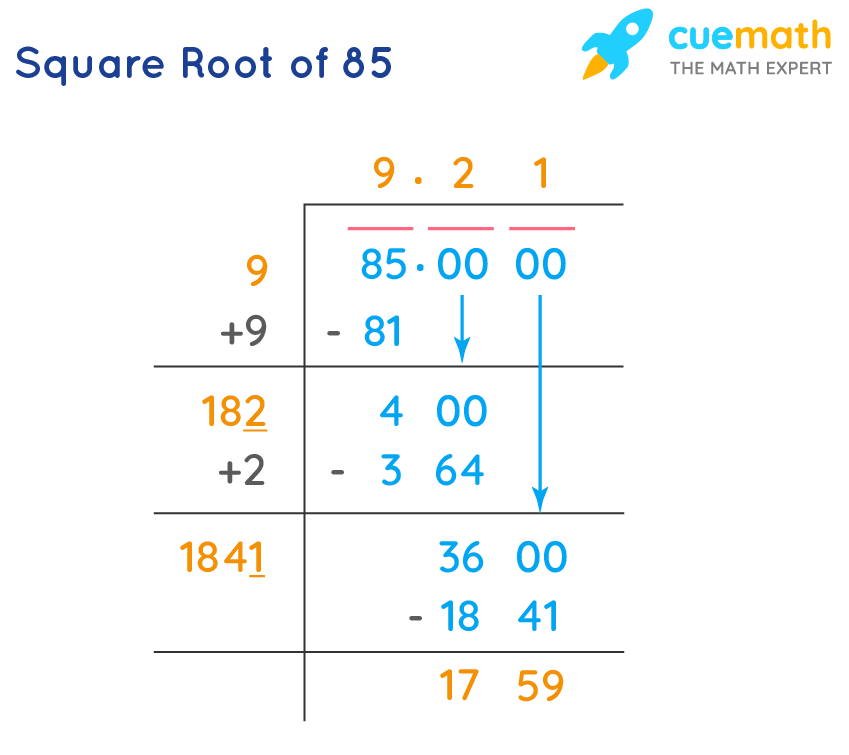
Long Division Method
- Pair the digits from right to left: 76.
- Find a number that, when squared, is less than or equal to 76. Here, 8 × 8 = 64.
- Subtract 64 from 76 to get 12. Bring down a pair of zeros to get 1200.
- Double the divisor (8) to get 16. Find a digit (7) such that 167 × 7 ≤ 1200.
- Repeat the process to get more decimal places.
Using the long division method, \(\sqrt{76} \approx 8.717\).
Properties of the Square Root of 76
- It is an irrational number.
- It cannot be expressed as a simple fraction.
- It is a real number.
Example Problems
- Example 1: Evaluate \((2\sqrt{19} + \sqrt{76}) \times (4\sqrt{19} - \sqrt{76})\)
Solution: \(\sqrt{76} = 2\sqrt{19}\)
Thus, \((2\sqrt{19} + \sqrt{76}) = (2\sqrt{19} + 2\sqrt{19}) = 4\sqrt{19}\)
And, \((4\sqrt{19} - \sqrt{76}) = (4\sqrt{19} - 2\sqrt{19}) = 2\sqrt{19}\)
Therefore, \((2\sqrt{19} + \sqrt{76}) \times (4\sqrt{19} - \sqrt{76}) = 4\sqrt{19} \times 2\sqrt{19} = 8 \times 19 = 152\). - Example 2: Find the circumference of a circle with an area of \(76\pi\) square inches.
Solution: The area of a circle is \(\pi r^2\). Given, \(\pi r^2 = 76\pi\), we get \(r^2 = 76\), thus \(r = \sqrt{76} \approx 8.717\). The circumference is \(2\pi r \approx 2 \times \pi \times 8.717 \approx 54.63\) inches.
Using Technology
You can calculate the square root of 76 using a calculator or in Excel/Google Sheets with the formula =SQRT(76). This will give the result approximately 8.717797887.
Conclusion
The square root of 76 is a useful number in various mathematical contexts, particularly in algebra and geometry. It is an irrational number and can be approximated in both decimal and simplified radical forms.

READ MORE:
Introduction
The square root of 76 is an important mathematical concept with various applications in different fields. Understanding the square root of a number helps in solving equations, analyzing geometric shapes, and more. In this guide, we will explore the definition, calculation methods, and practical uses of the square root of 76. The square root of 76, denoted as \( \sqrt{76} \), is an irrational number that cannot be expressed as a simple fraction. Its approximate value is:
\[ \sqrt{76} \approx 8.717797887 \]
To understand this concept in depth, we will cover the following topics:
- Definition and Basic Concepts
- Mathematical Representation
- Methods to Calculate Square Root
- Long Division Method
- Simplified Radical Form
- Using Calculators and Computers
- Excel and Google Sheets Functions
- Approximation and Rounding
- Applications in Geometry
- Real-World Examples
- Rational vs Irrational Numbers
- Perfect Squares and Imperfect Squares
- Common Questions and FAQs
By the end of this guide, you will have a comprehensive understanding of the square root of 76 and its significance in various mathematical and practical contexts.
Definition and Basic Concepts
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical notation, the square root of 76 is represented as √76.
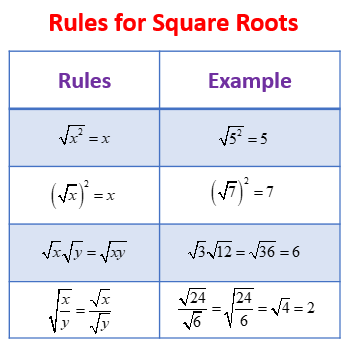
Basic properties of square roots include:
- Non-Negative Results: The square root of a non-negative number is always non-negative. For example, the square root of 76 is a positive real number.
- Principal Square Root: The principal square root is the positive square root of a number. For 76, the principal square root is denoted as √76.
- Irrational Numbers: Many square roots, including √76, are irrational numbers, meaning they cannot be expressed as a simple fraction. Their decimal representation is non-repeating and non-terminating.
Mathematically, the square root function is denoted as:
The square root of 76 can be understood through the following concepts:
- Radical Notation: The symbol √ is called the radical sign, and the number under the radical sign is called the radicand. Here, 76 is the radicand.
- Exponentiation: The square root of a number can also be expressed using exponents. For instance, √76 is equivalent to 76 raised to the power of 1/2:
- Estimating Square Roots: The square root of 76 is not an integer. It lies between 8 and 9 because 8² = 64 and 9² = 81. By refining the estimate, we find that √76 ≈ 8.7178.
Mathematical Representation
The square root of 76 is represented mathematically as:
\[
\sqrt{76}
\]
This value can be expressed in several ways:
- Decimal Form: The square root of 76 is approximately 8.7178.
- Fractional Form: There is no exact fractional representation since 76 is not a perfect square.
- Radical Form: The square root of 76 can be simplified by factoring out the perfect square within it: \[ \sqrt{76} = \sqrt{4 \times 19} = \sqrt{4} \times \sqrt{19} = 2\sqrt{19} \]
Therefore, the simplified radical form of the square root of 76 is \( 2\sqrt{19} \).
In conclusion, the square root of 76 can be represented in various forms depending on the context of the problem and the desired precision.
Methods to Calculate Square Root
There are several methods to calculate the square root of 76, each with varying degrees of precision and complexity. Here, we outline some of the most common methods:
- Long Division Method:
- Pair the digits of the number from right to left. For 76, we have one pair: (76).
- Find the largest number whose square is less than or equal to the first pair. In this case, 82 = 64.
- Write 8 as the first digit of the result.
- Subtract 64 from 76, giving a remainder of 12. Bring down a pair of zeros to get 1200.
- Double the result obtained so far (8), and write it with a blank next to it: 16_.
- Find the largest digit (x) such that 16x * x is less than or equal to 1200. This digit is 7, since 167 * 7 = 1169.
- Write 7 as the next digit of the result, giving 8.7.
- Repeat the process to get more digits of the square root.
- Prime Factorization Method:
- Factorize 76 into its prime factors: 76 = 22 × 19.
- Write the square root using these factors: \[ \sqrt{76} = \sqrt{2^2 \times 19} = \sqrt{2^2} \times \sqrt{19} = 2\sqrt{19} \]
- This method provides a simplified radical form but not a decimal approximation.
- Using a Calculator:
Most calculators have a square root function. Simply enter 76 and press the square root button to get an approximation, which is about 8.7178.
- Newton's Method (Iterative Method):
- Make an initial guess (x0) for the square root. Let's start with x0 = 8.
- Use the iterative formula: \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{76}{x_n} \right) \]
- Calculate the next approximation: \[ x_1 = \frac{1}{2} \left( 8 + \frac{76}{8} \right) \approx 8.5 \]
- Repeat the process until the desired precision is reached.
Each method has its own advantages, with calculators providing quick results and methods like the long division and Newton's method offering deeper insight into the mathematical process.

Using Calculators and Computers
Calculating the square root of 76 using calculators and computers is quick and straightforward. Here are the steps and methods for different devices and software:
- Using a Scientific Calculator:
- Turn on the calculator and ensure it is in standard mode.
- Enter the number 76 using the keypad.
- Press the square root (√) button. This button is usually labeled with the square root symbol.
- The display will show the square root of 76, which is approximately 8.7178.
- Using a Graphing Calculator:
- Turn on the graphing calculator and access the calculation mode.
- Enter 76 on the keypad.
- Press the square root (√) button. If not directly available, it might be found under a secondary function key (usually labeled "2nd" or "Shift").
- The calculator will display the result: approximately 8.7178.
- Using a Computer:
- Windows Calculator:
- Open the Calculator app from the Start menu.
- Select the "Scientific" mode to access the square root function.
- Enter 76 and click the square root (√) button to get the result: approximately 8.7178.
- Mac Calculator:
- Open the Calculator app from the Applications folder.
- Ensure the calculator is in scientific mode by selecting "View" > "Scientific" from the menu.
- Enter 76 and click the square root (√) button to display the result: approximately 8.7178.
- Using Online Calculators:
- Open a web browser and search for an online calculator or use specific sites like Google's calculator.
- Enter 76 in the input field and press the square root (√) button or type "sqrt(76)" if using a search engine calculator.
- The result, approximately 8.7178, will be displayed instantly.
- Windows Calculator:
- Using Spreadsheet Software:
- Microsoft Excel:
- Open Excel and select a cell.
- Type the formula
=SQRT(76)in the selected cell. - Press Enter, and the cell will display the result: approximately 8.7178.
- Google Sheets:
- Open Google Sheets and select a cell.
- Enter the formula
=SQRT(76)in the selected cell. - Press Enter, and the cell will show the result: approximately 8.7178.
- Microsoft Excel:
Using calculators and computers simplifies the process of finding the square root of 76, providing quick and accurate results with minimal effort.
Excel and Google Sheets Functions
Both Microsoft Excel and Google Sheets provide built-in functions to calculate the square root of a number easily. Here are the steps to find the square root of 76 using these functions:
Microsoft Excel
- Open Excel: Launch Microsoft Excel on your computer.
- Select a Cell: Click on the cell where you want the result to appear.
- Enter the Formula: Type the following formula in the selected cell:
\[
=SQRT(76)
\] - Press Enter: Press the Enter key. The cell will now display the square root of 76, which is approximately 8.7178.
- Using a Cell Reference: If the number 76 is in cell A1, you can use:
This allows for dynamic calculations if the value in A1 changes.
\[
=SQRT(A1)
\]
Google Sheets
- Open Google Sheets: Go to Google Sheets and open a new or existing spreadsheet.
- Select a Cell: Click on the cell where you want the result to appear.
- Enter the Formula: Type the following formula in the selected cell:
\[
=SQRT(76)
\] - Press Enter: Press the Enter key. The cell will now display the square root of 76, which is approximately 8.7178.
- Using a Cell Reference: If the number 76 is in cell A1, you can use:
This allows for dynamic calculations if the value in A1 changes.
\[
=SQRT(A1)
\]
These functions in Excel and Google Sheets make it simple to calculate square roots and perform other mathematical operations quickly and accurately.
Approximation and Rounding
Approximating and rounding the square root of 76 can be done through various methods to achieve the desired precision. Here are the steps to approximate and round the square root of 76:
Approximation Methods
- Using a Calculator: Enter 76 into a calculator and press the square root button. The calculator will display approximately 8.7178.
- Manual Approximation:
- Identify perfect squares close to 76. We know that:
- \( \sqrt{64} = 8 \)
- \( \sqrt{81} = 9 \)
- Refine the approximation by testing midpoints:
- Try 8.5: \( 8.5^2 = 72.25 \) (too low)
- Try 8.7: \( 8.7^2 = 75.69 \) (very close)
- Try 8.72: \( 8.72^2 = 76.0384 \) (a bit high)
- Identify perfect squares close to 76. We know that:
Rounding Techniques
The square root of 76 can be rounded to different decimal places depending on the required precision:
- Nearest Integer: Round 8.7178 to the nearest whole number, which is 9.
- One Decimal Place: Round 8.7178 to one decimal place:
- Look at the second decimal place (1). Since it is less than 5, round down.
- Result: 8.7
- Two Decimal Places: Round 8.7178 to two decimal places:
- Look at the third decimal place (7). Since it is 5 or greater, round up.
- Result: 8.72
- Three Decimal Places: Round 8.7178 to three decimal places:
- Look at the fourth decimal place (8). Since it is 5 or greater, round up.
- Result: 8.718
Approximating and rounding the square root of 76 allows you to work with a more manageable number while maintaining a useful level of precision for different applications.
Applications in Geometry
The square root of 76 has various applications in geometry, particularly in problems involving distances, areas, and right triangles. Here are some detailed examples and applications:
Distance Between Two Points
In coordinate geometry, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by the distance formula:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
Suppose we have points (2, 3) and (10, 11). The distance \(d\) can be calculated as follows:
- Calculate the differences: \( x_2 - x_1 = 10 - 2 = 8 \) and \( y_2 - y_1 = 11 - 3 = 8 \).
- Square the differences: \( 8^2 = 64 \) and \( 8^2 = 64 \).
- Add the squares: \( 64 + 64 = 128 \).
- Take the square root: \( d = \sqrt{128} = \sqrt{64 \times 2} = 8\sqrt{2} \approx 11.3137 \).
Right Triangles
In right triangles, the Pythagorean theorem relates the lengths of the sides:
\[
a^2 + b^2 = c^2
\]
where \(c\) is the hypotenuse. If one leg is 8 and the hypotenuse is \(\sqrt{76}\), we can find the other leg.
- Let \( a = 8 \) and \( c = \sqrt{76} \).
- Apply the Pythagorean theorem: \[ 8^2 + b^2 = (\sqrt{76})^2 \]
- Simplify: \[ 64 + b^2 = 76 \]
- Solve for \( b^2 \): \[ b^2 = 76 - 64 = 12 \]
- Find \( b \): \[ b = \sqrt{12} = 2\sqrt{3} \]
Area of a Circle
The area \(A\) of a circle is given by:
\[
A = \pi r^2
\]
where \( r \) is the radius. If the radius is the square root of 76, the area can be calculated as follows:
- Radius \( r = \sqrt{76} \).
- Substitute into the area formula: \[ A = \pi (\sqrt{76})^2 = \pi \times 76 \approx 238.76 \]
These examples illustrate how the square root of 76 can be applied to various geometric problems, aiding in calculations involving distances, right triangles, and areas.

Real-World Examples
The square root of 76 has practical applications in various real-world scenarios. Here are some detailed examples of how it can be used:
Construction and Architecture
In construction and architecture, precise measurements are crucial. Suppose an architect is designing a rectangular garden with an area of 76 square meters and needs to determine the side length for a square section within the garden.
- Determine the Side Length: To find the side length of a square with an area of 76 square meters:
\[
\text{Side length} = \sqrt{76} \approx 8.7178 \text{ meters}
\]
Physics and Engineering
In physics and engineering, the square root of 76 might be used to calculate the resultant vector in a 2D plane or the magnitude of a force.
- Resultant Vector: If two perpendicular forces, one of 8 units and the other of 6 units, act on an object, the magnitude of the resultant force \( R \) can be calculated using the Pythagorean theorem:
However, if the resultant force is known to be \(\sqrt{76}\), it could represent a combined effect in another scenario.
\[
R = \sqrt{8^2 + 6^2} = \sqrt{64 + 36} = \sqrt{100} = 10
\]
Navigation and GPS
In navigation and GPS technology, calculating distances between points on a map is essential. The square root of 76 can represent such a distance.
- Distance Calculation: For two points on a map, if the difference in latitude and longitude coordinates translates to a distance of 76 square units:
\[
\text{Distance} = \sqrt{76} \approx 8.7178 \text{ units}
\]
Astronomy
Astronomers might use the square root of 76 in calculations related to the distances between celestial objects or in deriving other astronomical measurements.
- Distance Between Stars: If the distance between two stars in a certain unit is represented as 76, the actual distance would be:
\[
\text{Distance} = \sqrt{76} \approx 8.7178 \text{ units}
\]
Everyday Life
Even in everyday scenarios, the square root of 76 might come up in situations like home improvement, sports, or other activities requiring precise measurements.
- Home Improvement: When laying out a square patio or garden with an area of 76 square feet, knowing the side length helps in planning:
\[
\text{Side length} = \sqrt{76} \approx 8.7178 \text{ feet}
\] - Sports: In sports like track and field, calculating the hypotenuse of a right triangle formed by running paths could involve the square root of 76.
These examples demonstrate the versatility and utility of the square root of 76 in various fields, emphasizing its importance in both professional and everyday contexts.
Rational vs Irrational Numbers
Understanding the difference between rational and irrational numbers is essential in mathematics. Let's explore these concepts and see how the square root of 76 fits in.
Rational Numbers
A rational number is any number that can be expressed as the quotient or fraction \(\frac{p}{q}\) of two integers, where \(p\) and \(q\) are integers and \(q \neq 0\). Rational numbers can be either terminating or repeating decimals.
- Examples of rational numbers include:
- \(\frac{1}{2} = 0.5\)
- \(\frac{3}{4} = 0.75\)
- \(\frac{1}{3} = 0.3333\ldots\) (repeating decimal)
Irrational Numbers
An irrational number cannot be expressed as a simple fraction. Irrational numbers have non-terminating, non-repeating decimal expansions.
- Examples of irrational numbers include:
- \(\pi \approx 3.14159\ldots\)
- \(e \approx 2.71828\ldots\)
- \(\sqrt{2} \approx 1.41421\ldots\)
Is the Square Root of 76 Rational or Irrational?
To determine whether \(\sqrt{76}\) is rational or irrational, we need to check if 76 is a perfect square.
- Perfect Squares: Numbers like 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100 are perfect squares because they can be expressed as the square of an integer.
- 76 is not a perfect square because there is no integer \( n \) such that \( n^2 = 76 \).
- Therefore, \(\sqrt{76}\) cannot be expressed as a fraction of two integers.
Since \(\sqrt{76}\) cannot be written as a fraction and its decimal form is non-terminating and non-repeating, it is classified as an irrational number.
Conclusion
The square root of 76 is an irrational number. This distinction is crucial for understanding its properties and behavior in various mathematical contexts. Recognizing whether a number is rational or irrational helps in solving equations, analyzing number properties, and performing accurate calculations.
Perfect Squares and Imperfect Squares
In mathematics, perfect squares and imperfect squares are fundamental concepts that help us understand the nature of numbers and their roots. Below, we will explore these concepts in detail, providing definitions, properties, and examples.
Perfect Squares
A perfect square is an integer that is the square of another integer. In other words, if \( n \) is an integer, then \( n^2 \) is a perfect square. Here are some key properties and examples:
- Every perfect square is a non-negative integer.
- Perfect squares have an odd number of total divisors.
- Examples of perfect squares include 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100.
The sequence of perfect squares can be represented as:
\[ 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, \ldots \]
Mathematically, the \( n \)-th perfect square can be expressed as:
\[ n^2 \]
where \( n \) is a positive integer.
Imperfect Squares
An imperfect square is a number that is not a perfect square. This means it cannot be expressed as the square of an integer. Imperfect squares are also referred to as non-perfect squares or simply non-square numbers. Some characteristics and examples include:
- Imperfect squares can be integers or non-integers.
- These numbers do not have an exact integer square root.
- Examples of imperfect squares include 2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, 18, 19, 20, 21, 22, 23, 24, 26, 27, 28, 29, 30, etc.
Unlike perfect squares, imperfect squares cannot be written in the form \( n^2 \) where \( n \) is an integer. Instead, their square roots are irrational numbers, meaning they cannot be expressed as a simple fraction and their decimal representation is non-repeating and non-terminating.
For example, the square root of 76 is an imperfect square, which can be expressed as:
\[ \sqrt{76} \approx 8.717797887 \]
Since 76 is not a perfect square, its square root is an irrational number.
Comparison Table
To better understand the difference between perfect squares and imperfect squares, let's look at a comparison table:
| Number | Perfect Square | Square Root |
|---|---|---|
| 4 | Yes | 2 |
| 9 | Yes | 3 |
| 16 | Yes | 4 |
| 76 | No | \( \sqrt{76} \approx 8.717797887 \) |
| 50 | No | \( \sqrt{50} \approx 7.071067812 \) |
Understanding the difference between perfect and imperfect squares is crucial for various mathematical applications, including algebra, geometry, and number theory. By recognizing these distinctions, we can better grasp the properties of numbers and their behaviors.
Common Questions and FAQs
-
What is the square root of 76 in the simplest form?
The square root of 76 in its simplest form is expressed as \( 2\sqrt{19} \).
-
How do you find the square root of 76?
The square root of 76 can be found using the long division method. As 76 is not a perfect square, this method provides an approximation.
- Pair the digits from right to left.
- Find the largest number whose square is less than or equal to 76.
- Use this number as the divisor and quotient, subtract the product from 76, and bring down a pair of zeros.
- Double the quotient, and find a new digit to continue the process until you reach the desired precision.
-
What is the approximate square root of 76?
The square root of 76 is approximately \( 8.71779788 \).
-
Is the square root of 76 rational or irrational?
The square root of 76 is irrational because it cannot be expressed as a simple fraction and its decimal form is non-terminating and non-repeating.
-
Is the square root of 76 a real number?
Yes, the square root of 76 is a real number.
-
How do you calculate the square root of 76 using a calculator?
You can use a scientific calculator or online tools. In Excel or Google Sheets, use the formula
=SQRT(76)to find the square root. -
What is the relationship between the square root of 76 and geometry?
In geometry, the square root of 76 can be used to find the side length of a square with an area of 76 square units. It also appears in the calculation of the diagonal length in right triangles where the legs have specific lengths.

Video hướng dẫn cách đơn giản hóa căn bậc hai của 76. Học cách tính toán sqrt(76) một cách dễ dàng và chính xác.
Làm thế nào để đơn giản hóa căn bậc hai của 76: sqrt(76)
READ MORE:
Cách đơn giản hóa căn bậc hai của số 76: Hướng dẫn chi tiết về cách tính và giản lược căn bậc hai của số 76.
Cách đơn giản hóa căn bậc hai của 76