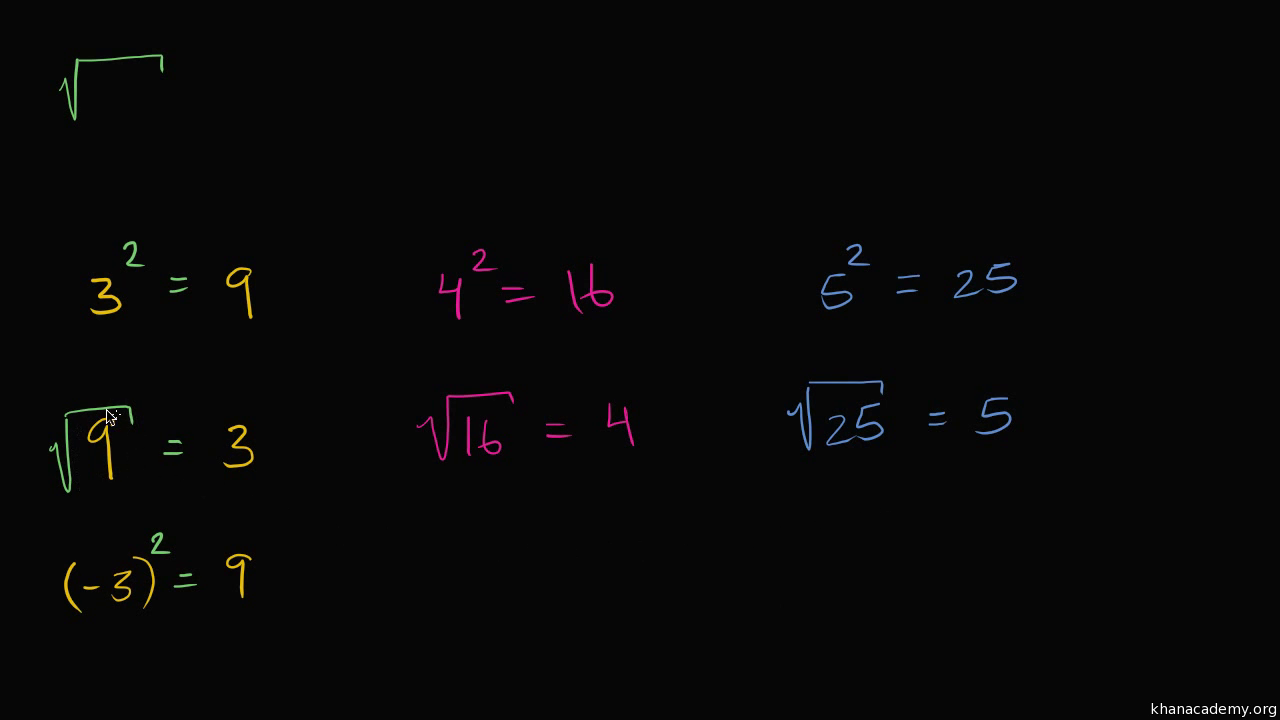Topic square root practice problems: Welcome to our comprehensive guide on square root practice problems! This article is designed to help you master the concept of square roots, providing a range of problems and solutions to enhance your understanding. Whether you're a student or a math enthusiast, you'll find valuable tips and exercises to improve your skills.
Table of Content
- Square Root Practice Problems
- Introduction to Square Roots
- Understanding Square Roots
- Square Root of Decimals
- Square Root of Fractions
- Simplifying Square Roots
- Solving Quadratic Equations using Square Roots
- Square Root Practice Problems
- Prime Factorization Method for Square Roots
- Common Square Root Mistakes and How to Avoid Them
- Interactive Square Root Quizzes
- Advanced Square Root Problems
- Applications of Square Roots in Real Life
- YOUTUBE: Xem video này để học cách đơn giản hóa căn bậc hai một cách hiệu quả.
Square Root Practice Problems
Here are some examples and practice problems to help you master square root calculations. Each example includes a step-by-step solution to guide you through the process.
Examples
-
Find the square root of 25:
\(\sqrt{25} = 5\)
Explanation: 5 multiplied by itself gives 25.
-
Find the square root of 121:
\(\sqrt{121} = 11\)
Explanation: 11 multiplied by itself gives 121.
-
Find the square root of 32:
\(\sqrt{32} = 4\sqrt{2}\)
Explanation: \(\sqrt{32} = \sqrt{16 \times 2} = 4\sqrt{2}\)
-
Find the square root of 50:
\(\sqrt{50} = 5\sqrt{2}\)
Explanation: \(\sqrt{50} = \sqrt{25 \times 2} = 5\sqrt{2}\)
-
Find the square root of 132:
\(\sqrt{132} = 2\sqrt{33}\)
Explanation: \(\sqrt{132} = \sqrt{4 \times 33} = 2\sqrt{33}\)
Practice Problems
- Find the square root of 1024 by prime factorization.
- Find the square root of 256 by prime factorization.
- Find the square root of 2025 by prime factorization.
- Find the square root of 36 by prime factorization.
- Find the square root of 3136 by prime factorization.
Solutions
-
Find the square root of 1024 by prime factorization:
Solution: \(\sqrt{1024} = 32\)
Explanation: \(1024 = 2^{10}\). \(\sqrt{2^{10}} = 2^5 = 32\)
-
Find the square root of 256 by prime factorization:
Solution: \(\sqrt{256} = 16\)
Explanation: \(256 = 2^8\). \(\sqrt{2^8} = 2^4 = 16\)
-
Find the square root of 2025 by prime factorization:
Solution: \(\sqrt{2025} = 45\)
Explanation: \(2025 = 5^2 \times 3^4\). \(\sqrt{5^2 \times 3^4} = 5 \times 3^2 = 45\)
-
Find the square root of 36 by prime factorization:
Solution: \(\sqrt{36} = 6\)
Explanation: \(36 = 2^2 \times 3^2\). \(\sqrt{2^2 \times 3^2} = 2 \times 3 = 6\)
-
Find the square root of 3136 by prime factorization:
Solution: \(\sqrt{3136} = 56\)
Explanation: \(3136 = 2^6 \times 7^2\). \(\sqrt{2^6 \times 7^2} = 2^3 \times 7 = 8 \times 7 = 56\)
Additional Resources

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4 because 4 × 4 = 16. Understanding square roots is fundamental in mathematics, especially in algebra and geometry. Below is a detailed guide to help you grasp the concept of square roots step by step.
Key Concepts
- Definition: If \( x \) is a number, then the square root of \( x \) is a number \( y \) such that \( y^2 = x \). It is often represented as \( \sqrt{x} \).
- Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For example, the square roots of 9 are 3 and -3.
- Principal Square Root: The principal square root is the non-negative root and is denoted by \( \sqrt{x} \).
Examples
Consider the following examples to understand square roots better:
| Number (x) | Square Root (√x) |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
Steps to Find Square Roots
- Identify the Perfect Square: Determine if the number is a perfect square (e.g., 1, 4, 9, 16).
- Factorization Method: Break down the number into its prime factors and pair them to find the square root.
- Long Division Method: For non-perfect squares, use the long division method to find an approximate value.
Square roots are essential in various mathematical problems and real-life applications, such as calculating areas, solving quadratic equations, and analyzing scientific data. Mastering the concept of square roots will significantly enhance your mathematical skills and problem-solving abilities.
Understanding Square Roots
Understanding square roots is crucial for solving various mathematical problems. A square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). Let's delve into the core concepts and methods to understand square roots comprehensively.
Basic Concepts
- Definition: The square root of \( x \), denoted as \( \sqrt{x} \), is the value that satisfies \( y^2 = x \).
- Positive and Negative Roots: Every positive number has two square roots: one positive (principal square root) and one negative. For example, the square roots of 25 are 5 and -5.
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are whole numbers.
Methods to Find Square Roots
- Prime Factorization:
- Break the number into its prime factors.
- Pair the prime factors.
- Multiply one number from each pair to find the square root.
- Long Division Method:
- Group the digits in pairs starting from the decimal point.
- Find the largest number whose square is less than or equal to the first group.
- Subtract the square of the number from the first group and bring down the next group.
- Double the quotient and find a digit to add to it such that the new number, when multiplied by the new digit, is less than or equal to the current dividend.
- Repeat the process for subsequent pairs.
Examples
Here are some examples to illustrate the concept:
| Number (x) | Square Root (√x) |
|---|---|
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
Applications
- Geometry: Calculating the side length of squares and right triangles.
- Algebra: Solving quadratic equations and simplifying expressions.
- Science: Analyzing physical phenomena and data.
By mastering the understanding of square roots, you can solve complex problems more effectively and apply these concepts in various mathematical and real-life scenarios.
Square Root of Decimals
Finding the square root of decimals can be a bit more challenging than finding the square root of whole numbers, but with the right methods, it becomes manageable. Below, we'll explore step-by-step processes to find the square root of decimal numbers using different techniques.
Methods to Find the Square Root of Decimals
- Convert to Fraction Method:
- Convert the decimal to a fraction. For example, \(0.25 = \frac{25}{100}\).
- Simplify the fraction if possible. In this case, \( \frac{25}{100} = \frac{1}{4} \).
- Find the square root of the numerator and the denominator separately. \( \sqrt{\frac{1}{4}} = \frac{\sqrt{1}}{\sqrt{4}} = \frac{1}{2} \).
- Convert the fraction back to a decimal if necessary. Here, \( \frac{1}{2} = 0.5 \).
- Long Division Method:
- Group the decimal number into pairs of digits starting from the decimal point. For example, \( 0.5625 \) is grouped as \( 56 \) and \( 25 \).
- Find the largest number whose square is less than or equal to the first pair (56). Here, 7 works because \( 7^2 = 49 \) and 8 is too high because \( 8^2 = 64 \).
- Subtract the square from the first pair and bring down the next pair. \( 56 - 49 = 7 \). Bring down 25 to get 725.
- Double the current quotient (7) to get 14, then find a digit (5) that when placed next to 14 and multiplied by itself is less than or equal to 725. Here, 145 × 5 = 725.
- Repeat the process for additional precision.
Examples
Here are some examples of finding the square root of decimals:
| Decimal | Square Root |
|---|---|
| 0.01 | 0.1 |
| 0.25 | 0.5 |
| 0.36 | 0.6 |
| 0.49 | 0.7 |
| 0.64 | 0.8 |
Practice Problems
- Find the square root of 0.81
- Find the square root of 0.09
- Find the square root of 0.04
- Find the square root of 0.16
Understanding how to find the square root of decimals is essential for various mathematical applications, from basic arithmetic to more advanced calculations. Practice these methods to enhance your skills and confidence in dealing with decimal square roots.
Square Root of Fractions
Finding the square root of fractions involves a straightforward process that can be simplified by understanding a few key concepts. Below, we'll explore step-by-step methods to find the square root of fractional numbers using different techniques.
Methods to Find the Square Root of Fractions
- Separate the Numerator and Denominator:
- Identify the numerator and the denominator of the fraction. For example, in the fraction \( \frac{9}{16} \), the numerator is 9 and the denominator is 16.
- Find the square root of the numerator and the denominator separately. In this case, \( \sqrt{9} = 3 \) and \( \sqrt{16} = 4 \).
- Combine the results to form the square root of the fraction. Therefore, \( \sqrt{\frac{9}{16}} = \frac{3}{4} \).
- Simplification Before Taking the Square Root:
- Check if the fraction can be simplified before finding the square root. For example, \( \frac{50}{200} \) can be simplified to \( \frac{1}{4} \).
- Find the square root of the simplified fraction. In this case, \( \sqrt{\frac{1}{4}} = \frac{1}{2} \).
Examples
Here are some examples of finding the square root of fractions:
| Fraction | Square Root |
|---|---|
| \( \frac{1}{9} \) | \( \frac{1}{3} \) |
| \( \frac{4}{25} \) | \( \frac{2}{5} \) |
| \( \frac{16}{81} \) | \( \frac{4}{9} \) |
| \( \frac{49}{100} \) | \( \frac{7}{10} \) |
| \( \frac{36}{49} \) | \( \frac{6}{7} \) |
Practice Problems
- Find the square root of \( \frac{25}{36} \)
- Find the square root of \( \frac{1}{64} \)
- Find the square root of \( \frac{49}{121} \)
- Find the square root of \( \frac{81}{100} \)
Understanding how to find the square root of fractions is an essential skill that can simplify many mathematical problems. Practice these methods to enhance your proficiency in working with fractional square roots.

Simplifying Square Roots
Simplifying square roots involves reducing the expression to its simplest form. This process makes it easier to work with square roots in mathematical problems. Below, we'll outline the step-by-step method to simplify square roots effectively.
Steps to Simplify Square Roots
- Prime Factorization:
- Find the prime factors of the number under the square root. For example, for \( \sqrt{72} \), the prime factors of 72 are \( 2^3 \times 3^2 \).
- Pair the prime factors. In this case, \( 2^3 \) has one pair of 2s and one leftover 2, and \( 3^2 \) has one pair of 3s.
- Bring one factor from each pair outside the square root. Here, \( \sqrt{72} = \sqrt{2^3 \times 3^2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
- Simplify Using Perfect Squares:
- Identify the largest perfect square factor of the number under the square root. For example, in \( \sqrt{50} \), the largest perfect square factor is 25.
- Rewrite the square root as a product of the square root of the perfect square and the square root of the remaining factor. Thus, \( \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} \).
- Simplify the square root of the perfect square. Here, \( \sqrt{25} = 5 \), so \( \sqrt{50} = 5\sqrt{2} \).
Examples
Here are some examples of simplifying square roots:
| Original Square Root | Simplified Form |
|---|---|
| \( \sqrt{18} \) | \( 3\sqrt{2} \) |
| \( \sqrt{45} \) | \( 3\sqrt{5} \) |
| \( \sqrt{72} \) | \( 6\sqrt{2} \) |
| \( \sqrt{98} \) | \( 7\sqrt{2} \) |
| \( \sqrt{200} \) | \( 10\sqrt{2} \) |
Practice Problems
- Simplify \( \sqrt{32} \)
- Simplify \( \sqrt{50} \)
- Simplify \( \sqrt{75} \)
- Simplify \( \sqrt{108} \)
Mastering the process of simplifying square roots will help you solve mathematical problems more efficiently and accurately. Practice these methods to become proficient in working with square roots.
Solving Quadratic Equations using Square Roots
Solving quadratic equations using square roots is a straightforward method when the equation can be written in the form \( ax^2 = c \). Below, we'll explore the step-by-step process to solve quadratic equations using square roots.
Steps to Solve Quadratic Equations using Square Roots
- Isolate the \( x^2 \) term:
Ensure that the equation is in the form \( ax^2 = c \). If it is not, rearrange it. For example, given the equation \( 2x^2 = 18 \), divide both sides by 2 to get \( x^2 = 9 \).
- Take the square root of both sides:
Apply the square root to both sides of the equation to solve for \( x \). Remember to consider both the positive and negative roots. For \( x^2 = 9 \), taking the square root of both sides gives \( x = \pm \sqrt{9} \), resulting in \( x = \pm 3 \).
- Check the solutions:
Substitute the solutions back into the original equation to verify their correctness.
Examples
Let's look at some examples:
| Equation | Steps | Solutions |
|---|---|---|
| \( x^2 = 16 \) |
|
\( x = 4 \) or \( x = -4 \) |
| \( 4x^2 = 25 \) |
|
\( x = \frac{5}{2} \) or \( x = -\frac{5}{2} \) |
| \( x^2 - 49 = 0 \) |
|
\( x = 7 \) or \( x = -7 \) |
Practice Problems
- Solve \( x^2 = 81 \)
- Solve \( 3x^2 = 27 \)
- Solve \( x^2 - 64 = 0 \)
- Solve \( 5x^2 = 45 \)
Understanding how to solve quadratic equations using square roots is a fundamental skill in algebra. Practice these methods to become proficient in solving such equations efficiently and accurately.
Square Root Practice Problems
Practicing square root problems is essential for mastering the concept and applying it in various mathematical contexts. Below are a variety of problems designed to help you practice finding and simplifying square roots.
Basic Square Root Problems
These problems focus on finding the square roots of perfect squares.
- Find the square root of 49.
- Find the square root of 144.
- Find the square root of 169.
- Find the square root of 225.
- Find the square root of 400.
Simplifying Square Roots
These problems require simplifying square roots to their simplest form.
- Simplify \( \sqrt{50} \).
- Simplify \( \sqrt{72} \).
- Simplify \( \sqrt{98} \).
- Simplify \( \sqrt{200} \).
- Simplify \( \sqrt{288} \).
Square Roots of Fractions
These problems involve finding the square roots of fractions.
- Find the square root of \( \frac{25}{36} \).
- Find the square root of \( \frac{49}{64} \).
- Find the square root of \( \frac{16}{81} \).
- Find the square root of \( \frac{9}{100} \).
- Find the square root of \( \frac{4}{49} \).
Square Roots of Decimals
These problems focus on finding the square roots of decimal numbers.
- Find the square root of 0.25.
- Find the square root of 0.49.
- Find the square root of 0.64.
- Find the square root of 0.81.
- Find the square root of 0.09.
Quadratic Equations Using Square Roots
These problems require solving quadratic equations by using square roots.
- Solve \( x^2 = 64 \).
- Solve \( 4x^2 = 100 \).
- Solve \( x^2 - 49 = 0 \).
- Solve \( 9x^2 = 81 \).
- Solve \( x^2 - 16 = 0 \).
Working through these practice problems will help you become more comfortable with square roots and improve your problem-solving skills. Take your time to solve each problem step-by-step, and refer back to the methods outlined in previous sections if needed.
Prime Factorization Method for Square Roots
The prime factorization method for finding square roots involves breaking down a number into its prime factors. This method is especially useful for simplifying square roots of large numbers. Here is a detailed step-by-step guide to using the prime factorization method for square roots.
Steps to Find Square Roots Using Prime Factorization
- Find the Prime Factors:
Break down the number into its prime factors. For example, for \( \sqrt{72} \), the prime factors of 72 are 2, 2, 2, 3, and 3, which can be written as \( 2^3 \times 3^2 \).
- Pair the Prime Factors:
Group the prime factors into pairs. Each pair will contribute a single factor outside the square root. For \( 2^3 \times 3^2 \), we have one pair of 2s and one pair of 3s.
- Simplify the Expression:
For each pair of factors, take one factor out of the square root. Multiply these factors together. Any unpaired factors remain inside the square root. Thus, \( \sqrt{72} = \sqrt{2^3 \times 3^2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2} \).
Examples
Let's look at some examples to illustrate this method:
| Original Expression | Prime Factors | Simplified Form |
|---|---|---|
| \( \sqrt{50} \) | \( 2 \times 5^2 \) | \( 5\sqrt{2} \) |
| \( \sqrt{72} \) | \( 2^3 \times 3^2 \) | \( 6\sqrt{2} \) |
| \( \sqrt{98} \) | \( 2 \times 7^2 \) | \( 7\sqrt{2} \) |
| \( \sqrt{200} \) | \( 2^3 \times 5^2 \) | \( 10\sqrt{2} \) |
| \( \sqrt{288} \) | \( 2^5 \times 3^2 \) | \( 12\sqrt{2} \) |
Practice Problems
- Simplify \( \sqrt{18} \) using prime factorization.
- Simplify \( \sqrt{45} \) using prime factorization.
- Simplify \( \sqrt{75} \) using prime factorization.
- Simplify \( \sqrt{125} \) using prime factorization.
- Simplify \( \sqrt{162} \) using prime factorization.
Practicing the prime factorization method will help you become proficient in simplifying square roots. This method provides a clear and systematic approach to handling more complex square root problems.

Common Square Root Mistakes and How to Avoid Them
Understanding and simplifying square roots can be challenging, leading to common mistakes. Here are some frequent errors and tips on how to avoid them.
Common Mistakes
- Ignoring the Negative Square Root:
Square roots have both positive and negative values. For example, \( \sqrt{9} \) can be \( \pm 3 \). Always remember to consider both solutions when solving equations involving square roots.
- Incorrect Simplification:
When simplifying square roots, it is essential to factor the number correctly. For example, \( \sqrt{50} \neq 5\sqrt{2} \); instead, it should be simplified as \( \sqrt{50} = 5\sqrt{2} \). Ensure to pair factors correctly.
- Confusing Square and Square Root:
Students often confuse squaring a number with finding its square root. For example, \( 5^2 = 25 \) is not the same as \( \sqrt{25} = 5 \). Always distinguish between the two operations.
- Forgetting to Simplify Completely:
Sometimes, students stop simplifying too early. For example, \( \sqrt{72} \) should be simplified to \( 6\sqrt{2} \) instead of stopping at \( \sqrt{36 \times 2} \).
- Incorrect Handling of Square Roots of Fractions:
When dealing with fractions, remember that \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For example, \( \sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}} = \frac{2}{3} \).
How to Avoid These Mistakes
- Double-Check Your Work:
Always review your steps to ensure accuracy. Verify each factorization and simplification step.
- Practice Regularly:
The more you practice square roots, the more familiar you become with common pitfalls and correct methods.
- Use Visual Aids:
Visual aids like factor trees can help in understanding prime factorization and simplifying square roots correctly.
- Understand the Concepts:
Rather than just memorizing steps, make sure you understand why each step is performed. This conceptual understanding will help avoid mistakes.
- Seek Help When Needed:
If you're unsure about a particular problem or method, don't hesitate to ask a teacher or use educational resources for clarification.
By being aware of these common mistakes and following the tips to avoid them, you can improve your skills in working with square roots and ensure greater accuracy in your mathematical problems.
Interactive Square Root Quizzes
Test your understanding of square roots with these interactive quizzes. Each quiz contains a set of problems designed to reinforce your knowledge and skills in calculating square roots.
-
Basic Square Roots: This quiz covers fundamental concepts such as finding the square root of perfect squares.
-
Square Root of Decimals: Practice calculating square roots of decimal numbers.
-
Square Root of Fractions: Test your ability to compute square roots of fractional numbers.
-
Simplifying Square Roots: This quiz focuses on simplifying square roots by factoring.
-
Advanced Problems: Challenge yourself with more complex square root problems involving quadratic equations and real-life applications.
Each quiz is interactive, providing instant feedback to help you learn and improve. Whether you are a beginner or looking to sharpen your skills, these quizzes offer a practical way to enhance your understanding of square roots.
Advanced Square Root Problems
Explore challenging square root problems to deepen your mathematical skills and problem-solving abilities:
-
Quadratic Equations: Solve quadratic equations using square root methods, including both real and complex roots.
-
Radical Equations: Practice solving equations involving square roots and higher-order radicals.
-
Applications in Geometry: Apply square root concepts to solve geometric problems, such as finding lengths, areas, and volumes.
-
Real-Life Scenarios: Explore practical situations where understanding square roots is crucial, such as in engineering and physics.
-
Proofs and Theorems: Delve into proofs related to square roots and their properties, enhancing your understanding of mathematical principles.
These advanced problems are designed to challenge and expand your knowledge beyond basic arithmetic, preparing you for more complex mathematical endeavors.
Applications of Square Roots in Real Life
Discover how square roots are applied in various practical situations:
-
Engineering: Calculate forces, stresses, and structural stability in engineering designs.
-
Physics: Determine velocities, accelerations, and energies in physics calculations.
-
Finance: Assess risk and return rates using formulas involving square roots.
-
Measurement: Find distances, areas, and volumes in construction and surveying.
-
Computer Graphics: Generate smooth curves and animations using square root functions.
Understanding square roots is essential in these fields to solve complex problems efficiently and accurately, demonstrating the practical relevance of mathematical concepts in everyday applications.

Xem video này để học cách đơn giản hóa căn bậc hai một cách hiệu quả.
Video Hướng dẫn Cách Đơn Giản Hóa Căn Bậc Hai
READ MORE:
What are Square Roots? | Math with Mr. J
Đâu là Căn bậc hai? | Toán học với Thầy J