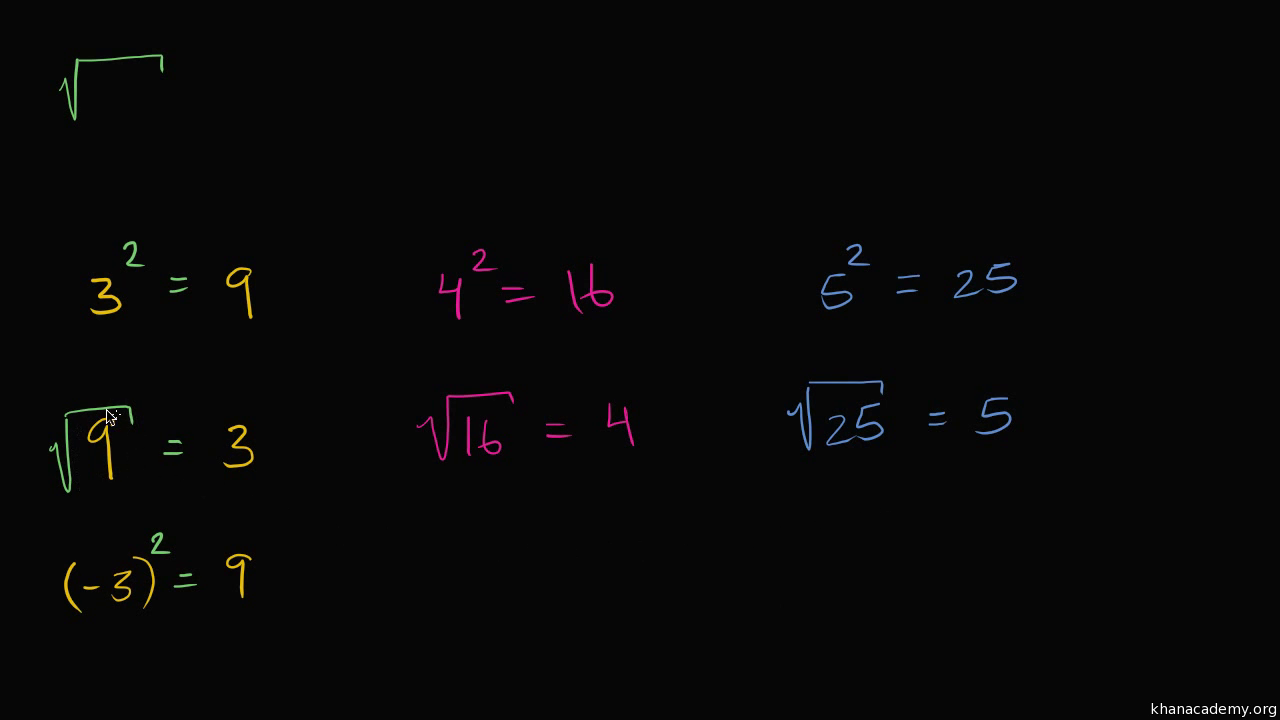Topic square root by hand: Discover the fascinating world of calculating square roots by hand! This guide will teach you proven methods like long division, prime factorization, and approximation. Enhance your math skills and gain confidence in solving square roots without a calculator. Perfect for students, teachers, and math enthusiasts alike.
Table of Content
- How to Calculate the Square Root by Hand
- Introduction to Square Roots
- Methods for Calculating Square Roots by Hand
- Step-by-Step Guide for Long Division Method
- Examples of Long Division Method
- Step-by-Step Guide for Prime Factorization Method
- Examples of Prime Factorization Method
- Step-by-Step Guide for Approximation Method
- Examples of Approximation Method
- Other Methods for Calculating Square Roots
- History of Square Root Calculation Methods
- Mathematical Principles Behind Square Roots
- Common Applications of Square Roots
- Frequently Asked Questions (FAQs)
- Conclusion
- YOUTUBE: Video hướng dẫn cách tính căn bậc hai bằng tay cho học sinh tiểu học. Khám phá phương pháp đơn giản và dễ hiểu để tính căn bậc hai một cách chính xác.
How to Calculate the Square Root by Hand
Calculating the square root of a number by hand can be done using several methods. Here, we'll outline a few common techniques: the Long Division Method, the Prime Factorization Method, and the Approximation Method.
Long Division Method
The Long Division Method is a systematic approach to finding the square root of a number:
- Group the digits in pairs, starting from the decimal point and moving both left and right.
- Find the largest number whose square is less than or equal to the first group. This is the first digit of the square root.
- Subtract the square of this number from the first group and bring down the next group of digits.
- Double the number already found and use it as a divisor to find the next digit of the square root. Repeat the process.
Example: √152.2756
- Pair the digits: 1 | 52. | 27 | 56
- Find the largest square less than or equal to 1. (1^2 = 1)
- Subtract and bring down the next group: (1 - 1 = 0) | 52
- Double the current digit (1): 2_ is the new divisor. Find the digit d such that (20+d)d ≤ 52. The digit is 2.
- Subtract and bring down the next group: (52 - 44 = 8) | 27
- Double the current digits (12): 24_ is the new divisor. Find the digit d such that (240+d)d ≤ 827. The digit is 3.
- Repeat until the desired precision is reached.
Prime Factorization Method
The Prime Factorization Method involves breaking down the number into its prime factors and simplifying:
- Write the number as a product of its prime factors.
- Pair the prime factors in groups of two.
- Take one factor from each pair and multiply them together to get the square root.
Example: √360
- Prime factors of 360: 2 × 2 × 2 × 3 × 3 × 5
- Pair the factors: (2 × 2), (2 × 3 × 3), (5)
- Take one factor from each pair: 2, 3, and √5
- Multiply: 2 × 3 × √5 = 6√5
Approximation Method
The Approximation Method is useful for estimating the square root of a number:
- Find two perfect squares between which the number lies.
- Estimate a value between those two squares.
- Use averaging to refine the estimate: If your initial guess is x, then a better approximation is (x + n/x) / 2.
Example: √50
- 50 lies between 7^2 (49) and 8^2 (64).
- Estimate: 7.5
- Refine: (7.5 + 50/7.5) / 2 ≈ 7.071
Using these methods, you can calculate square roots by hand with practice and patience.

READ MORE:
Introduction to Square Roots
Square roots are fundamental mathematical operations that help us find a number which, when multiplied by itself, yields the original number. The square root of a number \( n \) is denoted as \( \sqrt{n} \). For example, the square root of 9 is 3, since \( 3 \times 3 = 9 \).
Understanding square roots is crucial in various fields such as algebra, geometry, and real-world applications like physics and engineering. Calculating square roots by hand can be done using several methods, each with its own steps and benefits. Below are the key techniques:
- Long Division Method: A systematic approach that involves grouping digits and finding successive approximations.
- Prime Factorization Method: Involves breaking down the number into its prime factors and simplifying.
- Approximation Method: Useful for estimating square roots by finding two perfect squares between which the number lies and refining the estimate.
Each method provides a unique way to understand and calculate square roots, enhancing your mathematical skills and problem-solving abilities. Whether you're a student or a math enthusiast, mastering these techniques will give you confidence in tackling square root problems without the need for a calculator.
Methods for Calculating Square Roots by Hand
Calculating square roots by hand can be done through various methods, each offering a unique approach to understanding and solving square root problems. Here are the most commonly used methods:
Long Division Method
The Long Division Method is a step-by-step process that involves grouping digits and finding successive approximations to the square root.
- Group the digits of the number in pairs, starting from the decimal point and moving both left and right.
- Find the largest number whose square is less than or equal to the first group of digits. This number is the first digit of the square root.
- Subtract the square of this number from the first group of digits and bring down the next group of digits.
- Double the current result and use it as a divisor. Find the digit that, when added to this divisor and multiplied by the same digit, gives a product less than or equal to the current remainder. This digit is the next digit of the square root.
- Repeat the process until the desired precision is achieved.
Prime Factorization Method
The Prime Factorization Method involves breaking down the number into its prime factors and then simplifying to find the square root.
- Write the number as a product of its prime factors.
- Group the prime factors in pairs.
- Take one factor from each pair and multiply them together to get the square root.
- If there are any unpaired factors, the square root will be irrational and can be left in the radical form.
Approximation Method
The Approximation Method is useful for estimating square roots when a high degree of precision is not required.
- Identify two perfect squares between which the number lies.
- Estimate an initial value between these two squares.
- Use the formula \( x_{n+1} = \frac{x_n + \frac{n}{x_n}}{2} \) to refine the estimate, where \( x_n \) is the current approximation.
- Repeat the process until the estimate is sufficiently accurate.
Each method has its own advantages and applications, making it possible to choose the most appropriate one depending on the context and desired precision. Mastering these techniques will enhance your mathematical proficiency and provide a deeper understanding of square roots.
Step-by-Step Guide for Long Division Method
The long division method is a manual technique to find the square root of a number. Here is a step-by-step guide to help you understand this method:
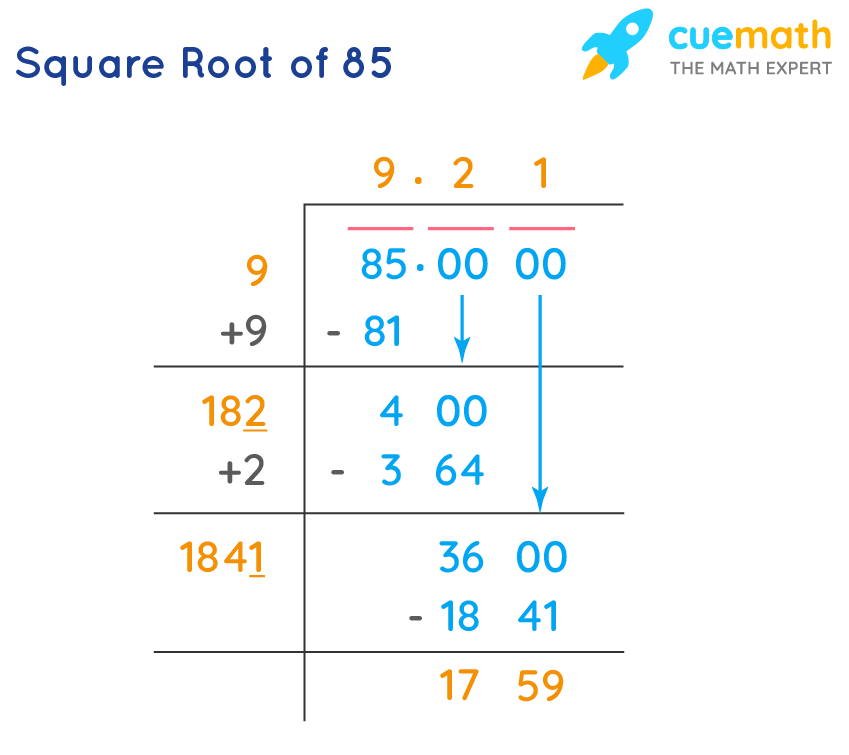
Step 1: Separate the Digits into Pairs
Starting from the decimal point (or the rightmost digit if no decimal point), separate the digits into pairs by placing a bar over each pair of digits. For example, to find the square root of 152.2756, separate it into pairs: 1|52.27|56.
Step 2: Find the Largest Number Whose Square is Less Than or Equal to the First Pair
Find the largest number whose square is less than or equal to the first pair. Write this number above the pair, and subtract its square from the first pair. For 152.2756, the first pair is 1. The largest number whose square is ≤ 1 is 1. Write 1 above, and subtract 1² (1) from 1, resulting in 0.
1 | 1 52.27 56 | -1 | 0 52.27 56 Step 3: Bring Down the Next Pair of Digits
Bring down the next pair of digits next to the remainder. This becomes the new dividend. For our example, bring down 52, making it 52.
Step 4: Double the Quotient and Determine the Next Digit
Double the current quotient (1 in this case) and place it next to the new dividend. Find a digit X such that (2×quotientX)×X is less than or equal to the current dividend. Place X in the quotient and subtract (2×quotientX)×X from the current dividend. In this case, 2×1=2, so we need to find a number X such that 20X×X ≤ 52.
The number X is 2 because 22×2=44, which is less than 52. Write 2 in the quotient and subtract 44 from 52.
1.2 | 1 52.27 56 | -1 | 0 52.27 | -44 | 8.27 Step 5: Repeat the Process
Continue repeating steps 3 and 4 with the next pairs of digits. For the next pair, bring down 27 to get 827. Double the quotient (12), making it 24. Find X such that (24X)×X ≤ 827. In this case, X is 3 because 243×3 = 729, which is less than 827. Subtract 729 from 827 to get 98.
1.23 | 1 52.27 56 | -1 | 0 52.27 | -44 | 8.27 | -729 | 98 Step 6: Continue for More Precision
Continue the process with additional pairs of digits for more precision. For example, bring down the next pair (56), making it 9856. Double the quotient (123), making it 246. Find X such that (246X)×X ≤ 9856. Repeat the steps until the desired precision is achieved.
Examples of Long Division Method
The long division method for finding square roots can be illustrated with a few examples. Let's walk through two different examples to understand the process clearly.
Example 1: Square Root of 2025
Group the digits of 2025 into pairs from right to left: 20 25.
Find the largest integer whose square is less than or equal to the leftmost group (20). In this case, 42 = 16 ≤ 20 and 52 = 25 > 20. So, the integer is 4.
Write 4 as the first digit of the square root and subtract 16 from 20. Bring down the next pair of digits (25), giving us 425.
Double the current digit of the root (4), resulting in 8. Find a digit x such that 8x * x is less than or equal to 425. In this case, 85 * 5 = 425, so x is 5.
Write 5 as the next digit of the root. Subtract 425 from 425, which gives 0, indicating the calculation is complete. Thus, √2025 = 45.
Example 2: Square Root of 683
Group the digits of 683 into pairs from right to left, adding a pair of zeros for accuracy: 6 83.00.
Find the largest integer whose square is less than or equal to the leftmost group (6). In this case, 22 = 4 ≤ 6 and 32 = 9 > 6. So, the integer is 2.
Write 2 as the first digit of the square root and subtract 4 from 6. Bring down the next pair of digits (83), giving us 283.
Double the current digit of the root (2), resulting in 4. Find a digit x such that 4x * x is less than or equal to 283. In this case, 46 * 6 = 276, so x is 6.
Write 6 as the next digit of the root. Subtract 276 from 283, giving 7. Bring down the next pair of digits (00), giving us 700.
Double the current root (26), resulting in 52. Find a digit x such that 52x * x is less than or equal to 700. In this case, 521 * 1 = 521, so x is 1.
Write 1 as the next digit of the root and subtract 521 from 700, giving 179. Bring down the next pair of zeros (00), giving us 17900.
Continue the process to achieve the desired accuracy. The square root of 683 to two decimal places is approximately 26.13.
These examples show the step-by-step procedure for finding the square root of a number using the long division method, illustrating the importance of grouping digits, finding suitable digits through trial and error, and performing arithmetic operations accurately to achieve the desired precision.

Step-by-Step Guide for Prime Factorization Method
The Prime Factorization Method is a straightforward way to find the square root of a number by breaking it down into its prime factors. Here's a step-by-step guide:
-
Write down the number: Identify the number whose square root you want to find and write it down. For example, let's find the square root of 3600.
-
Prime factorize the number: Divide the number into its smallest prime factors. You can do this by dividing the number with prime numbers (2, 3, 5, 7, etc.) until you cannot divide it any further.
For 3600, the prime factorization is:
- 3600 ÷ 2 = 1800
- 1800 ÷ 2 = 900
- 900 ÷ 2 = 450
- 450 ÷ 2 = 225
- 225 ÷ 3 = 75
- 75 ÷ 3 = 25
- 25 ÷ 5 = 5
- 5 ÷ 5 = 1
So, the prime factors of 3600 are \(2^4 \times 3^2 \times 5^2\).
-
Group the factors into pairs: Arrange the obtained prime factors in ascending order and group them into pairs of equal factors.
For 3600, the pairs are:
- \(2^2\) and \(2^2\)
- \(3^2\)
- \(5^2\)
-
Write down one factor from each pair: Choose one factor from each pair and write them down.
From the pairs above, we take 2, 3, and 5.
-
Multiply those factors: Multiply all the chosen factors together to find the square root.
\(\sqrt{3600} = 2 \times 3 \times 5 = 30\)
Therefore, the square root of 3600 using the Prime Factorization Method is 30.
Examples of Prime Factorization Method
The Prime Factorization Method involves breaking down a number into its prime factors and then using those factors to determine the square root. Here are a few examples to illustrate this method:
Example 1: Square Root of 144
- Prime Factorization of 144:
\(144 = 2 \times 2 \times 2 \times 2 \times 3 \times 3\)
- Group the prime factors into pairs:
\((2 \times 2) \times (2 \times 2) \times (3 \times 3)\)
- Take one factor from each pair:
\(2 \times 2 \times 3 = 12\)
- The square root of 144 is:
\(\sqrt{144} = 12\)
Example 2: Square Root of 81
- Prime Factorization of 81:
\(81 = 3 \times 3 \times 3 \times 3\)
- Group the prime factors into pairs:
\((3 \times 3) \times (3 \times 3)\)
- Take one factor from each pair:
\(3 \times 3 = 9\)
- The square root of 81 is:
\(\sqrt{81} = 9\)
Example 3: Square Root of 196
- Prime Factorization of 196:
\(196 = 2 \times 2 \times 7 \times 7\)
- Group the prime factors into pairs:
\((2 \times 2) \times (7 \times 7)\)
- Take one factor from each pair:
\(2 \times 7 = 14\)
- The square root of 196 is:
\(\sqrt{196} = 14\)
Example 4: Square Root of 225
- Prime Factorization of 225:
\(225 = 3 \times 3 \times 5 \times 5\)
- Group the prime factors into pairs:
\((3 \times 3) \times (5 \times 5)\)
- Take one factor from each pair:
\(3 \times 5 = 15\)
- The square root of 225 is:
\(\sqrt{225} = 15\)
Example 5: Square Root of 625
- Prime Factorization of 625:
\(625 = 5 \times 5 \times 5 \times 5\)
- Group the prime factors into pairs:
\((5 \times 5) \times (5 \times 5)\)
- Take one factor from each pair:
\(5 \times 5 = 25\)
- The square root of 625 is:
\(\sqrt{625} = 25\)
Step-by-Step Guide for Approximation Method
The approximation method is a useful technique for estimating square roots by hand. This method involves making an educated guess and refining it through iteration. Follow these detailed steps to calculate the square root of a number using the approximation method:
-
Step 1: Choose an Initial Guess
Start by selecting an initial guess that is close to the actual square root. You can use simple rounding or nearby perfect squares to help make your guess.
- For example, to find the square root of 50, you might choose 7 as your initial guess because \(7^2 = 49\), which is close to 50.
-
Step 2: Divide and Average
Divide the number you are finding the square root of by your initial guess. Then, find the average of the initial guess and the result of the division.
- \[\text{New guess} = \frac{\text{Initial guess} + \frac{\text{Number}}{\text{Initial guess}}}{2}\]
- Using the example above: \[\text{New guess} = \frac{7 + \frac{50}{7}}{2} = \frac{7 + 7.14}{2} = 7.07\]
-
Step 3: Repeat the Process
Use the new guess obtained in Step 2 as your initial guess and repeat the divide and average process until the guess stabilizes and changes very little.
- Using the example above: \[\text{New guess} = \frac{7.07 + \frac{50}{7.07}}{2} = \frac{7.07 + 7.07}{2} = 7.071\]
- Continue this process until the result is accurate enough for your purposes.
-
Step 4: Verify the Result
After several iterations, the guess should be very close to the actual square root. You can verify this by squaring your final guess and comparing it to the original number.
- Using the example above: \(7.071 \approx \sqrt{50}\) because \(7.071^2 \approx 50\).
The approximation method is an effective way to estimate square roots without the use of a calculator. With practice, you can quickly improve the accuracy of your approximations.
Examples of Approximation Method
To illustrate the approximation method for calculating square roots by hand, let's go through a couple of detailed examples.
Example 1: Finding the Square Root of 45
-
Step 1: Choose an Initial Guess
Let's start with an initial guess of 7, because \(7^2 = 49\), which is close to 45.
-
Step 2: Divide and Average
Divide 45 by the initial guess, and then average the quotient with the initial guess.
- Calculation: \[\text{New guess} = \frac{7 + \frac{45}{7}}{2} = \frac{7 + 6.43}{2} = 6.715\]
-
Step 3: Repeat the Process
Use the new guess to repeat the divide and average process.
- Calculation: \[\text{New guess} = \frac{6.715 + \frac{45}{6.715}}{2} = \frac{6.715 + 6.702}{2} = 6.7085\]
-
Step 4: Verify the Result
Square the final guess to verify accuracy:
- Calculation: \(6.7085^2 = 45\) (approximately)
Example 2: Finding the Square Root of 20
-
Step 1: Choose an Initial Guess
Let's start with an initial guess of 4, because \(4^2 = 16\), which is close to 20.
-
Step 2: Divide and Average
Divide 20 by the initial guess, and then average the quotient with the initial guess.
- Calculation: \[\text{New guess} = \frac{4 + \frac{20}{4}}{2} = \frac{4 + 5}{2} = 4.5\]
-
Step 3: Repeat the Process
Use the new guess to repeat the divide and average process.
- Calculation: \[\text{New guess} = \frac{4.5 + \frac{20}{4.5}}{2} = \frac{4.5 + 4.444}{2} = 4.472\]
- Repeat again: \[\text{New guess} = \frac{4.472 + \frac{20}{4.472}}{2} = \frac{4.472 + 4.472}{2} = 4.472\]
-
Step 4: Verify the Result
Square the final guess to verify accuracy:
- Calculation: \(4.472^2 = 20\) (approximately)
These examples demonstrate how the approximation method can be used to estimate square roots with increasing accuracy through iteration.

Other Methods for Calculating Square Roots
Besides the long division and approximation methods, there are several other techniques for calculating square roots by hand. Here, we explore three alternative methods:
1. Newton's Method
Newton's Method, also known as the Newton-Raphson method, is an iterative approach to finding increasingly accurate approximations of square roots. Here's a step-by-step guide:
Make an initial guess \( g \) for the square root of \( x \). A good starting point is to use a number close to the actual square root.
Use the formula: \( g_{new} = \frac{g + \frac{x}{g}}{2} \)
Replace \( g \) with \( g_{new} \) and repeat the process until the desired level of accuracy is achieved.
For example, to find the square root of 30:
- Initial guess: \( g = 5 \)
- First iteration: \( g_{new} = \frac{5 + \frac{30}{5}}{2} = 5.5 \)
- Second iteration: \( g_{new} = \frac{5.5 + \frac{30}{5.5}}{2} \approx 5.477 \)
Each iteration brings the approximation closer to the actual square root.
2. Babylonian Method
The Babylonian method, an ancient technique similar to Newton's method, is also iterative and involves the following steps:
Make an initial guess \( g \).
Update the guess using: \( g_{new} = \frac{g + \frac{x}{g}}{2} \)
Repeat the process until the approximation stabilizes.
This method converges quickly to the square root.
3. Bakhshali Approximation
The Bakhshali approximation, an ancient Indian method, provides a quick estimate of square roots:
Choose a close approximate square root \( a \).
Calculate the difference \( d = \frac{x - a^2}{2a} \).
Find the square root using: \( \sqrt{x} \approx a + d - \frac{d^2}{2a} \).
For instance, to estimate \( \sqrt{10} \):
- Choose \( a = 3 \) (since \( 3^2 = 9 \))
- Calculate \( d = \frac{10 - 9}{2 \cdot 3} = \frac{1}{6} \approx 0.167 \)
- Approximate \( \sqrt{10} \approx 3 + 0.167 - \frac{(0.167)^2}{6} \approx 3.162 \)
This method provides a very close approximation with minimal calculation.
History of Square Root Calculation Methods
The history of square root calculation methods spans several millennia and reflects the development of mathematical understanding and techniques across different cultures.
Ancient Civilizations
Early methods for calculating square roots date back to ancient Babylon and Egypt. The Babylonians, around 1800 BCE, used an iterative method similar to the modern-day Heron’s method to approximate square roots. This method involved a series of guesses that converged to the correct value.
Greek Contributions
The Greeks made significant contributions to the theory of square roots. The Pythagoreans were among the first to study irrational numbers, which are closely related to square roots. Euclid's "Elements," written around 300 BCE, includes geometric methods for finding square roots.
Chinese and Indian Mathematicians
In ancient China, mathematicians used a method similar to long division, known as the "extraction of roots," to find square roots. This method is documented in "The Nine Chapters on the Mathematical Art," a Chinese mathematical text from around 200 CE.
Indian mathematicians like Aryabhata (476-550 CE) and Brahmagupta (598-668 CE) also made notable contributions. Aryabhata described an algorithm for extracting square roots, while Brahmagupta developed rules for dealing with square roots of negative numbers.
Islamic Golden Age
During the Islamic Golden Age (8th to 14th centuries), mathematicians expanded on Greek and Indian knowledge. Al-Khwarizmi's works introduced systematic solutions to quadratic equations, involving square roots, to the Islamic world and later to Europe.
European Renaissance
In the 16th century, European mathematicians like Niccolò Tartaglia and Gerolamo Cardano further developed methods for solving polynomial equations, which often required finding square roots. The development of algebra and the notation we use today made these calculations more systematic.
Newton's Method
In the 17th century, Sir Isaac Newton developed an efficient iterative method for finding square roots, known as Newton's method or the Newton-Raphson method. This method uses calculus to refine approximations of roots and is still widely used in numerical analysis.
Modern Computational Methods
With the advent of computers in the 20th century, calculating square roots has become more efficient and precise. Algorithms like the digit-by-digit calculation method and various numerical methods are implemented in computer software to quickly and accurately compute square roots.
Conclusion
The journey of discovering and refining methods to calculate square roots illustrates the cumulative nature of mathematical knowledge. Each civilization built upon the discoveries of the previous ones, leading to the advanced techniques we use today.
Mathematical Principles Behind Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. The mathematical notation for square root is the radical symbol (√). For example, the square root of 9 is 3 because 3 × 3 = 9. Square roots have both positive and negative solutions because both (3 × 3) and (-3 × -3) equal 9.
Here are some fundamental principles behind square roots:
- Definition: The square root of a number \( x \) is a number \( r \) such that \( r^2 = x \). This can be written as \( \sqrt{x} = r \).
- Principal Square Root: The principal square root is the non-negative square root of a number. For example, while the square roots of 16 are 4 and -4, the principal square root is 4, denoted as \( \sqrt{16} = 4 \).
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are whole numbers (1, 2, 3, 4, and 5, respectively).
- Non-Perfect Squares: The square roots of non-perfect squares are irrational numbers. For instance, \( \sqrt{2} \approx 1.414 \), which cannot be expressed as a simple fraction and has an infinite number of non-repeating decimals.
Let's delve into some examples to illustrate these principles:
| x | x² | \( \sqrt{x} \) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 4 | 16 | 4 |
| 9 | 81 | 9 |
| 16 | 256 | 16 |
When dealing with square roots, there are a few important properties and rules:
- Product Property: \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \), valid when both \( a \) and \( b \) are non-negative.
- Quotient Property: \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \), valid when \( b \neq 0 \) and both \( a \) and \( b \) are non-negative.
These properties are crucial for simplifying square roots and solving equations involving square roots. Additionally, understanding the relationship between squares and square roots is fundamental in algebra and higher-level mathematics.
Common Applications of Square Roots
Square roots play a crucial role in various real-life applications across different fields. Below are some common applications of square roots:
-
Geometry and Measurement:
Square roots are used to calculate the length of sides in geometric shapes, especially right triangles using the Pythagorean theorem. For instance, if you know the lengths of two sides of a right triangle, you can find the third side.
-
Statistics:
In statistics, square roots are used to calculate standard deviation and variance. Standard deviation, which measures the amount of variation or dispersion in a set of values, is the square root of the variance.
-
Physics:
Square roots are used in various physical formulas, such as calculating the time it takes for an object to fall to the ground (using the formula \( t = \frac{\sqrt{h}}{4} \)), where \( h \) is the height in feet.
-
Finance:
In finance, square roots are used to calculate the volatility of stock returns. Volatility is a measure of how much a stock's price fluctuates, and it is derived by taking the square root of the variance of stock returns.
-
Engineering:
In engineering, square roots are essential for calculations involving stress and strain in materials, natural frequencies of structures, and other applications where precise measurements are crucial.
-
Computer Graphics:
In computer graphics, square roots are used to compute distances between points in both 2D and 3D space, which is essential for rendering images and animations accurately.
-
Navigation:
Square roots are used to calculate distances between points on a map, which is crucial for navigation in both aviation and maritime contexts. The distance formula in a plane uses the square root to determine the shortest path between two points.
-
Cryptography:
In cryptography, square roots are used in various algorithms for encryption and decryption, ensuring secure communication and data protection.

Frequently Asked Questions (FAQs)
Below are some common questions and answers related to calculating square roots by hand.
1. What is the simplest method to calculate square roots by hand?
The simplest method for calculating square roots by hand is the long division method. It involves pairing the digits of the number, finding approximate digits one by one, and refining the answer through iterations.
2. How accurate can manual square root calculations be?
Manual square root calculations can be very accurate if you continue the process to more decimal places. For instance, using methods like long division or Newton's method can give you precise results up to several decimal places.
3. What are some other methods to find square roots by hand?
Other methods include the prime factorization method, the approximation method (using average), and the method of continued fractions. Each method has its own advantages depending on the context and the number being evaluated.
4. Is it possible to calculate square roots of non-perfect squares manually?
Yes, it is possible to calculate the square roots of non-perfect squares manually using methods like the long division method. The result will be an approximation that can be refined to the desired precision.
5. Why is it important to learn to calculate square roots by hand?
Learning to calculate square roots by hand helps improve mathematical understanding and problem-solving skills. It also provides a deeper appreciation of how algorithms work and can be useful in situations where calculators are not available.
6. Can these methods be used to calculate cube roots or higher roots?
Yes, similar principles can be applied to calculate cube roots or higher roots, although the steps are more complex. Methods like Newton's method and trial and error can be adapted for these purposes.
7. What is the historical significance of square root calculations?
Calculating square roots has been important historically for various applications in architecture, astronomy, and engineering. Ancient mathematicians developed various methods that laid the groundwork for modern computational techniques.
8. Are there any shortcuts or tricks for estimating square roots?
Yes, there are several tricks for estimating square roots quickly. One common trick is to use the average method, where you guess a value, calculate its square, and adjust your guess accordingly. Another trick is to memorize squares of smaller numbers to aid in faster calculations.
9. How does the long division method work?
The long division method works by grouping the digits in pairs from right to left, finding the largest number whose square is less than the first pair, and then iteratively refining the result by considering each pair of digits. It is a systematic approach that breaks down the problem into manageable steps.
10. Can I use these methods for very large numbers?
Yes, these methods can be applied to very large numbers, although they may become time-consuming. For very large numbers, iterative methods like Newton's method are often more efficient and practical.
Conclusion
Calculating square roots by hand, although not commonly practiced today due to the prevalence of digital calculators, is a valuable skill that helps deepen one's understanding of mathematical principles. The various methods such as the long division method, the approximation method, and prime factorization each offer unique insights into the nature of square roots and their calculation.
The long division method, while meticulous, provides a precise approach and helps reinforce division and multiplication skills. The approximation method offers a more intuitive grasp, enabling quick estimates that can be refined to achieve greater accuracy. Prime factorization, on the other hand, connects square roots to the fundamental properties of numbers, highlighting the significance of prime numbers in mathematics.
Beyond the mechanical process, understanding how to calculate square roots by hand fosters a greater appreciation for the structure and patterns within mathematics. It underscores the importance of number sense and the relationships between different mathematical operations.
In everyday life, square roots find applications in areas ranging from geometry and physics to finance and engineering. Whether it's calculating areas, understanding quadratic equations, or analyzing data trends, the ability to compute square roots is integral to problem-solving in various fields.
By mastering these hand-calculation methods, one not only hones their mathematical skills but also gains a historical perspective on how mathematical practices have evolved. This knowledge can serve as a foundation for further exploration in mathematics and its applications.
Embrace the challenge of calculating square roots by hand, and you'll discover a rewarding journey that enhances both your mathematical proficiency and your appreciation for the elegance of numbers.
Video hướng dẫn cách tính căn bậc hai bằng tay cho học sinh tiểu học. Khám phá phương pháp đơn giản và dễ hiểu để tính căn bậc hai một cách chính xác.
Cách Tính Căn Bậc Hai Bằng Tay (Dành Cho Học Sinh Tiểu Học)
READ MORE:
Video hướng dẫn cách tính căn bậc hai bằng tay. Khám phá phương pháp đơn giản và dễ hiểu để tính căn bậc hai một cách chính xác.
Cách Tính Căn Bậc Hai Bằng Tay