Topic square root x derivative: Understanding the derivative of the square root of x is essential for mastering calculus. This article explores various methods to derive it, including the first principle, power rule, chain rule, product rule, and quotient rule, and provides practical examples and common mistakes to avoid. Let's dive into the fascinating world of derivatives!
Table of Content
- Derivative of the Square Root of x
- Introduction to Derivative of Square Root of x
- Definition and Formula
- Derivative Using the First Principle
- Derivative Using the Power Rule
- Derivative Using the Chain Rule
- Derivative Using the Product Rule
- Derivative Using the Quotient Rule
- Examples and Applications
- Derivative of Square Root of x+1
- Derivative of Square Root of 2x
- Derivative of Square Root of 3x
- Common Mistakes and Tips
- Conclusion
- YOUTUBE:
Derivative of the Square Root of x
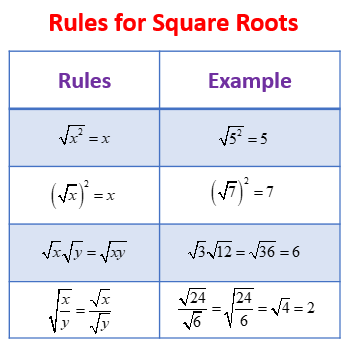
To find the derivative of the function \( f(x) = \sqrt{x} \), we can use the power rule for differentiation.
Step-by-Step Process
- Rewrite the square root function as a power of \( x \):
\( f(x) = \sqrt{x} = x^{1/2} \)
- Apply the power rule for derivatives, which states that if \( f(x) = x^n \), then \( f'(x) = nx^{n-1} \):
\( \frac{d}{dx} \left( x^{1/2} \right) = \frac{1}{2} x^{(1/2) - 1} \)
- Simplify the expression:
\( \frac{d}{dx} \left( x^{1/2} \right) = \frac{1}{2} x^{-1/2} \)
This can also be written as:
\( \frac{d}{dx} \left( \sqrt{x} \right) = \frac{1}{2} \cdot \frac{1}{\sqrt{x}} \)
Therefore:
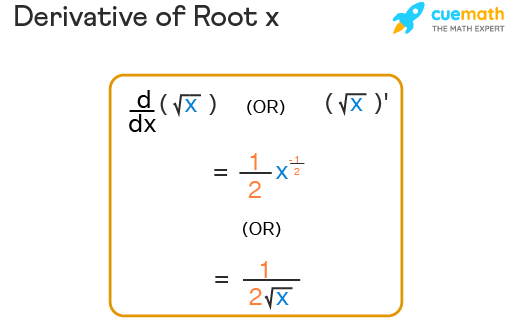
\( \frac{d}{dx} \left( \sqrt{x} \right) = \frac{1}{2\sqrt{x}} \)
Result
The derivative of the square root of \( x \) is:
Table Summary
| Function | Derivative |
|---|---|
| \( \sqrt{x} \) | \( \frac{1}{2\sqrt{x}} \) |
This derivative can be used in various calculus problems, particularly those involving rates of change and optimization where the function involves a square root.
READ MORE:
Introduction to Derivative of Square Root of x
The derivative of the square root of x is a fundamental concept in calculus, essential for understanding more complex functions. The square root function, denoted as \( \sqrt{x} \) or \( x^{1/2} \), has unique properties that we explore through different methods of differentiation.
In this section, we will cover:
- The definition and basic formula for the derivative of \( \sqrt{x} \)
- Step-by-step derivation using the first principle of derivatives
- Application of the power rule to find the derivative
- Using the chain rule for more complex functions involving \( \sqrt{x} \)
Let's start by understanding the basic definition and formula:
The derivative of a function \( f(x) \) at a point \( x \) is defined as:
\[
f'(x) = \lim_{{h \to 0}} \frac{f(x+h) - f(x)}{h}
\]
For the square root function \( f(x) = \sqrt{x} \), we use this definition to find its derivative:
- Substitute \( f(x) = \sqrt{x} \) into the definition:
\[
\frac{\sqrt{x+h} - \sqrt{x}}{h}
\] - Multiply the numerator and the denominator by the conjugate of the numerator:
\[
\frac{\sqrt{x+h} - \sqrt{x}}{h} \cdot \frac{\sqrt{x+h} + \sqrt{x}}{\sqrt{x+h} + \sqrt{x}} = \frac{(x+h) - x}{h(\sqrt{x+h} + \sqrt{x})} = \frac{h}{h(\sqrt{x+h} + \sqrt{x})}
\] - Simplify the expression:
\[
\frac{h}{h(\sqrt{x+h} + \sqrt{x})} = \frac{1}{\sqrt{x+h} + \sqrt{x}}
\] - Take the limit as \( h \) approaches 0:
\[
\lim_{{h \to 0}} \frac{1}{\sqrt{x+h} + \sqrt{x}} = \frac{1}{2\sqrt{x}}
\]
Therefore, the derivative of \( \sqrt{x} \) is:
\[
\frac{d}{dx}\sqrt{x} = \frac{1}{2\sqrt{x}}
\]
This result will be verified and further explored using various differentiation rules in the following sections.
Definition and Formula
The derivative of the square root of \( x \) is a key concept in calculus. It helps in understanding the rate at which the square root function changes. Here, we define the derivative and derive the formula step by step.
For a function \( f(x) = \sqrt{x} \), its derivative, denoted as \( f'(x) \) or \( \frac{d}{dx}\sqrt{x} \), measures the rate of change of \( \sqrt{x} \) with respect to \( x \).
The formula for the derivative of \( \sqrt{x} \) can be derived using the definition of the derivative and basic differentiation rules:
Step-by-Step Derivation:
- Rewrite the Function:
Express the square root function using exponent notation:
\[
f(x) = \sqrt{x} = x^{1/2}
\] - Apply the Power Rule:
The power rule states that for any function \( x^n \), the derivative is:
\[
\frac{d}{dx} x^n = n x^{n-1}
\]
Using this rule for \( n = 1/2 \):
\[
\frac{d}{dx} x^{1/2} = \frac{1}{2} x^{(1/2) - 1} = \frac{1}{2} x^{-1/2}
\] - Simplify the Result:
Rewrite \( x^{-1/2} \) as \( \frac{1}{\sqrt{x}} \):
\[
\frac{d}{dx} \sqrt{x} = \frac{1}{2} \cdot \frac{1}{\sqrt{x}} = \frac{1}{2\sqrt{x}}
\]
Therefore, the derivative of \( \sqrt{x} \) is given by:
\[
\frac{d}{dx} \sqrt{x} = \frac{1}{2\sqrt{x}}
\]
This formula indicates that the rate of change of \( \sqrt{x} \) decreases as \( x \) increases, reflecting the nature of the square root function.
Derivative Using the First Principle
The first principle of derivatives, also known as the definition of the derivative, provides a fundamental approach to finding the derivative of a function. For \( f(x) = \sqrt{x} \), we can use this principle to derive its derivative step by step.
Step-by-Step Derivation:
- Definition of the Derivative:
The derivative of a function \( f(x) \) at a point \( x \) is defined as:
\[
f'(x) = \lim_{{h \to 0}} \frac{f(x+h) - f(x)}{h}
\] - Substitute the Function:
For \( f(x) = \sqrt{x} \), substitute \( \sqrt{x} \) into the definition:
\[
f'(x) = \lim_{{h \to 0}} \frac{\sqrt{x+h} - \sqrt{x}}{h}
\] - Rationalize the Numerator:
To simplify the expression, multiply the numerator and the denominator by the conjugate of the numerator:
\[
\frac{\sqrt{x+h} - \sqrt{x}}{h} \cdot \frac{\sqrt{x+h} + \sqrt{x}}{\sqrt{x+h} + \sqrt{x}} = \frac{(\sqrt{x+h} - \sqrt{x})(\sqrt{x+h} + \sqrt{x})}{h(\sqrt{x+h} + \sqrt{x})} = \frac{(x+h) - x}{h(\sqrt{x+h} + \sqrt{x})}
\] - Simplify the Expression:
Simplify the numerator:
\[
\frac{h}{h(\sqrt{x+h} + \sqrt{x})} = \frac{1}{\sqrt{x+h} + \sqrt{x}}
\] - Take the Limit:
As \( h \) approaches 0, the expression simplifies to:
\[
\lim_{{h \to 0}} \frac{1}{\sqrt{x+h} + \sqrt{x}} = \frac{1}{2\sqrt{x}}
\]
Therefore, using the first principle, the derivative of \( \sqrt{x} \) is:
\[
\frac{d}{dx} \sqrt{x} = \frac{1}{2\sqrt{x}}
\]
This step-by-step approach provides a clear understanding of how the derivative of \( \sqrt{x} \) is derived from first principles.
Derivative Using the Power Rule
The power rule is a straightforward and widely used method for finding the derivative of functions of the form \( x^n \). For the square root function \( f(x) = \sqrt{x} \), we can apply the power rule to determine its derivative easily.
Step-by-Step Derivation:
- Rewrite the Function:
Express the square root function using exponent notation:
\[
f(x) = \sqrt{x} = x^{1/2}
\] - Apply the Power Rule:
The power rule states that for any function \( x^n \), the derivative is:
\[
\frac{d}{dx} x^n = n x^{n-1}
\]
Applying this rule for \( n = 1/2 \):
\[
\frac{d}{dx} x^{1/2} = \frac{1}{2} x^{(1/2) - 1} = \frac{1}{2} x^{-1/2}
\] - Simplify the Result:
Rewrite \( x^{-1/2} \) as \( \frac{1}{\sqrt{x}} \):
\[
\frac{d}{dx} x^{1/2} = \frac{1}{2} \cdot \frac{1}{\sqrt{x}} = \frac{1}{2\sqrt{x}}
\]
Therefore, using the power rule, the derivative of \( \sqrt{x} \) is:
\[
\frac{d}{dx} \sqrt{x} = \frac{1}{2\sqrt{x}}
\]
The power rule simplifies the differentiation process, providing a quick and efficient way to find the derivative of \( \sqrt{x} \).
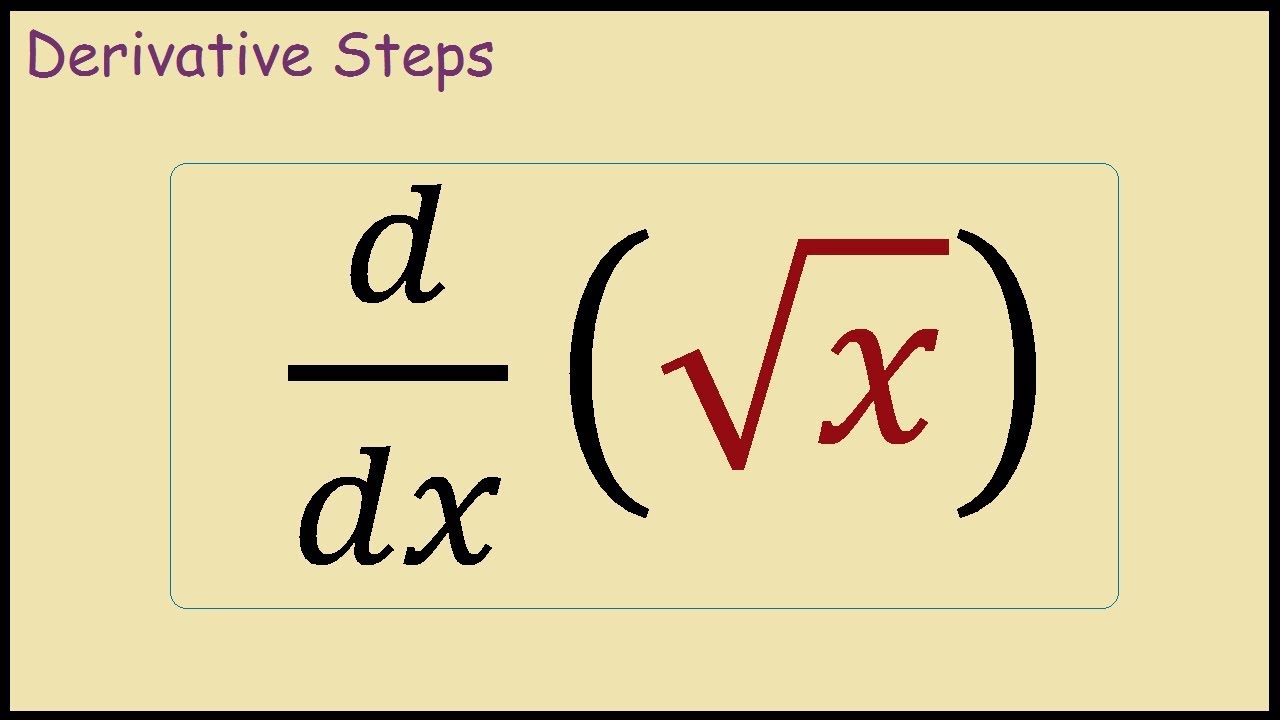
Derivative Using the Chain Rule
To find the derivative of the square root of \( x \) using the chain rule, we can follow these steps:
- Identify the outer function and the inner function.
- Apply the chain rule formula: \( (f(g(x)))' = f'(g(x)) \cdot g'(x) \).
Let's break down the steps:
The function we are differentiating is \( \sqrt{x} \), which can be written as \( (x^{1/2}) \).
- Outer function \( f(u) = u^{1/2} \)
- Inner function \( g(x) = x \)
According to the chain rule, we need to find the derivatives of the outer and inner functions:
- The derivative of the outer function \( f(u) = u^{1/2} \):
- \( f'(u) = \frac{1}{2}u^{-1/2} \)
- The derivative of the inner function \( g(x) = x \):
- \( g'(x) = 1 \)
Now apply the chain rule:
\[
\frac{d}{dx} \sqrt{x} = \frac{d}{dx} (x^{1/2}) = \frac{1}{2}(x)^{-1/2} \cdot 1
\]
Simplify the expression:
\[
\frac{d}{dx} \sqrt{x} = \frac{1}{2} \cdot \frac{1}{\sqrt{x}} = \frac{1}{2\sqrt{x}}
\]
Therefore, the derivative of \( \sqrt{x} \) using the chain rule is \( \frac{1}{2\sqrt{x}} \).
Derivative Using the Product Rule
The product rule is generally used when we have a function that is the product of two other functions. To use the product rule for finding the derivative of the square root of \( x \), we can rewrite the function in a form suitable for applying the product rule.
Let's consider the function \( \sqrt{x} \) and rewrite it as a product:
\[
\sqrt{x} = x^{1/2}
\]
We can express \( x^{1/2} \) as the product of two functions:
- \( u(x) = x \)
- \( v(x) = x^{-1/2} \)
Now, according to the product rule, if \( y = u(x) \cdot v(x) \), then:
\[
y' = u'(x) \cdot v(x) + u(x) \cdot v'(x)
\]
Let's find the derivatives of \( u(x) \) and \( v(x) \):
- \( u(x) = x \Rightarrow u'(x) = 1 \)
- \( v(x) = x^{-1/2} \Rightarrow v'(x) = -\frac{1}{2} x^{-3/2} \)
Now, apply the product rule:
\[
\frac{d}{dx} (x \cdot x^{-1/2}) = 1 \cdot x^{-1/2} + x \cdot \left( -\frac{1}{2} x^{-3/2} \right)
\]
Simplify the expression step by step:
- \( 1 \cdot x^{-1/2} = x^{-1/2} \)
- \( x \cdot \left( -\frac{1}{2} x^{-3/2} \right) = -\frac{1}{2} x^{-1/2} \)
Combine the terms:
\[
x^{-1/2} - \frac{1}{2} x^{-1/2} = \frac{1}{2} x^{-1/2}
\]
Therefore, the derivative of \( \sqrt{x} \) using the product rule is \( \frac{1}{2\sqrt{x}} \).
Derivative Using the Quotient Rule
The quotient rule is used when we want to find the derivative of a function that is the ratio of two differentiable functions. To use the quotient rule for finding the derivative of the square root of \( x \), we can rewrite the function in a form suitable for applying the quotient rule.
Let's consider the function \( \sqrt{x} \) and rewrite it as a quotient:
\[
\sqrt{x} = \frac{x}{x^{1/2}}
\]
We can express \( \sqrt{x} \) as the quotient of two functions:
- \( u(x) = x \)
- \( v(x) = x^{1/2} \)
According to the quotient rule, if \( y = \frac{u(x)}{v(x)} \), then:
\[
y' = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{(v(x))^2}
\]
Let's find the derivatives of \( u(x) \) and \( v(x) \):
- \( u(x) = x \Rightarrow u'(x) = 1 \)
- \( v(x) = x^{1/2} \Rightarrow v'(x) = \frac{1}{2} x^{-1/2} \)
Now, apply the quotient rule:
\[
\frac{d}{dx} \left( \frac{x}{x^{1/2}} \right) = \frac{1 \cdot x^{1/2} - x \cdot \left( \frac{1}{2} x^{-1/2} \right)}{(x^{1/2})^2}
\]
Simplify the expression step by step:
- \( 1 \cdot x^{1/2} = x^{1/2} \)
- \( x \cdot \left( \frac{1}{2} x^{-1/2} \right) = \frac{1}{2} x^{1/2} \)
- \( (x^{1/2})^2 = x \)
Combine the terms in the numerator:
\[
x^{1/2} - \frac{1}{2} x^{1/2} = \frac{1}{2} x^{1/2}
\]
Now, place the simplified numerator over the denominator:
\[
\frac{\frac{1}{2} x^{1/2}}{x} = \frac{1}{2} \cdot \frac{x^{1/2}}{x} = \frac{1}{2} \cdot x^{-1/2}
\]
Simplify further:
\[
\frac{1}{2} \cdot x^{-1/2} = \frac{1}{2\sqrt{x}}
\]
Therefore, the derivative of \( \sqrt{x} \) using the quotient rule is \( \frac{1}{2\sqrt{x}} \).
Examples and Applications
Understanding the derivative of the square root of \( x \) is crucial in various mathematical and real-world applications. Let's explore some examples and applications to see how this derivative is used.
Example 1: Finding the Slope of a Tangent Line
Suppose we need to find the slope of the tangent line to the curve \( y = \sqrt{x} \) at \( x = 4 \).
- First, find the derivative: \( \frac{d}{dx} \sqrt{x} = \frac{1}{2\sqrt{x}} \).
- Evaluate the derivative at \( x = 4 \):
\[
\left. \frac{1}{2\sqrt{x}} \right|_{x=4} = \frac{1}{2\sqrt{4}} = \frac{1}{2 \cdot 2} = \frac{1}{4}
\] - The slope of the tangent line at \( x = 4 \) is \( \frac{1}{4} \).
Example 2: Rate of Change
In a physics problem, suppose the distance \( s \) (in meters) traveled by an object is given by \( s = \sqrt{t} \), where \( t \) is the time in seconds. To find the velocity of the object at \( t = 9 \) seconds:
- First, find the derivative: \( \frac{d}{dt} \sqrt{t} = \frac{1}{2\sqrt{t}} \).
- Evaluate the derivative at \( t = 9 \):
\[
\left. \frac{1}{2\sqrt{t}} \right|_{t=9} = \frac{1}{2\sqrt{9}} = \frac{1}{2 \cdot 3} = \frac{1}{6}
\] - The velocity of the object at \( t = 9 \) seconds is \( \frac{1}{6} \) meters per second.
Application: Economics
In economics, the derivative of a function can represent the marginal cost or marginal revenue. Suppose the cost \( C \) (in dollars) to produce \( x \) units of a product is given by \( C = \sqrt{x} \). To find the marginal cost when \( x = 16 \) units:
- First, find the derivative: \( \frac{d}{dx} \sqrt{x} = \frac{1}{2\sqrt{x}} \).
- Evaluate the derivative at \( x = 16 \):
\[
\left. \frac{1}{2\sqrt{x}} \right|_{x=16} = \frac{1}{2\sqrt{16}} = \frac{1}{2 \cdot 4} = \frac{1}{8}
\] - The marginal cost at \( x = 16 \) units is \( \frac{1}{8} \) dollars per unit.
Application: Biology
In biology, the growth rate of a population can sometimes be modeled by functions involving square roots. If the population \( P \) of a certain species over time \( t \) (in years) is given by \( P = \sqrt{t} \), to find the growth rate at \( t = 25 \) years:
- First, find the derivative: \( \frac{d}{dt} \sqrt{t} = \frac{1}{2\sqrt{t}} \).
- Evaluate the derivative at \( t = 25 \):
\[
\left. \frac{1}{2\sqrt{t}} \right|_{t=25} = \frac{1}{2\sqrt{25}} = \frac{1}{2 \cdot 5} = \frac{1}{10}
\] - The growth rate of the population at \( t = 25 \) years is \( \frac{1}{10} \) units per year.
These examples demonstrate the diverse applications of the derivative of the square root of \( x \) in various fields such as mathematics, physics, economics, and biology.

Derivative of Square Root of x+1
To find the derivative of \( \sqrt{x+1} \), we can use the chain rule. The chain rule is useful when dealing with composite functions, where one function is nested inside another.
Let's break down the process step by step:
- Identify the outer function and the inner function.
- Apply the chain rule formula: \( (f(g(x)))' = f'(g(x)) \cdot g'(x) \).
For the function \( \sqrt{x+1} \), we can identify:
- Outer function: \( f(u) = \sqrt{u} = u^{1/2} \)
- Inner function: \( g(x) = x + 1 \)
Next, find the derivatives of the outer and inner functions:
- Derivative of the outer function: \( f'(u) = \frac{1}{2} u^{-1/2} = \frac{1}{2\sqrt{u}} \)
- Derivative of the inner function: \( g'(x) = 1 \)
Now, apply the chain rule:
\[
\frac{d}{dx} \sqrt{x+1} = \frac{d}{dx} (x+1)^{1/2} = \frac{1}{2} (x+1)^{-1/2} \cdot 1
\]
Simplify the expression:
\[
\frac{d}{dx} \sqrt{x+1} = \frac{1}{2} \cdot \frac{1}{\sqrt{x+1}} = \frac{1}{2\sqrt{x+1}}
\]
Therefore, the derivative of \( \sqrt{x+1} \) is \( \frac{1}{2\sqrt{x+1}} \).
Let's see an example of how this derivative can be used:
Example: Tangent Line to \( \sqrt{x+1} \) at \( x = 3 \)
- Find the derivative at \( x = 3 \):
\[
\left. \frac{1}{2\sqrt{x+1}} \right|_{x=3} = \frac{1}{2\sqrt{3+1}} = \frac{1}{2\sqrt{4}} = \frac{1}{2 \cdot 2} = \frac{1}{4}
\] - Find the value of the function at \( x = 3 \):
\[
y = \sqrt{3+1} = \sqrt{4} = 2
\] - Use the point-slope form of the equation of the tangent line:
\[
y - y_1 = m(x - x_1)
\]
where \( m \) is the slope and \( (x_1, y_1) \) is the point of tangency. - Substitute \( m = \frac{1}{4} \), \( x_1 = 3 \), and \( y_1 = 2 \):
\[
y - 2 = \frac{1}{4}(x - 3)
\]Therefore, the equation of the tangent line is:
\[
y = \frac{1}{4}x + \frac{5}{4}
\]
This example demonstrates how the derivative of \( \sqrt{x+1} \) can be used to find the slope of the tangent line to the curve at a specific point.
Derivative of Square Root of 2x
To find the derivative of \( \sqrt{2x} \), we will use the chain rule. The chain rule is particularly useful for finding the derivative of composite functions, where one function is nested within another.
Let's break down the process step by step:
- Identify the outer function and the inner function.
- Apply the chain rule formula: \( (f(g(x)))' = f'(g(x)) \cdot g'(x) \).
For the function \( \sqrt{2x} \), we can identify:
- Outer function: \( f(u) = \sqrt{u} = u^{1/2} \)
- Inner function: \( g(x) = 2x \)
Next, find the derivatives of the outer and inner functions:
- Derivative of the outer function: \( f'(u) = \frac{1}{2} u^{-1/2} = \frac{1}{2\sqrt{u}} \)
- Derivative of the inner function: \( g'(x) = 2 \)
Now, apply the chain rule:
\[
\frac{d}{dx} \sqrt{2x} = \frac{d}{dx} (2x)^{1/2} = \frac{1}{2} (2x)^{-1/2} \cdot 2
\]
Simplify the expression:
\[
\frac{d}{dx} \sqrt{2x} = \frac{1}{2} \cdot \frac{1}{\sqrt{2x}} \cdot 2 = \frac{1}{\sqrt{2x}}
\]
Therefore, the derivative of \( \sqrt{2x} \) is \( \frac{1}{\sqrt{2x}} \).
Let's see an example of how this derivative can be used:
Example: Tangent Line to \( \sqrt{2x} \) at \( x = 4 \)
- Find the derivative at \( x = 4 \):
\[
\left. \frac{1}{\sqrt{2x}} \right|_{x=4} = \frac{1}{\sqrt{2 \cdot 4}} = \frac{1}{\sqrt{8}} = \frac{1}{2\sqrt{2}}
\] - Find the value of the function at \( x = 4 \):
\[
y = \sqrt{2 \cdot 4} = \sqrt{8} = 2\sqrt{2}
\] - Use the point-slope form of the equation of the tangent line:
\[
y - y_1 = m(x - x_1)
\]
where \( m \) is the slope and \( (x_1, y_1) \) is the point of tangency. - Substitute \( m = \frac{1}{2\sqrt{2}} \), \( x_1 = 4 \), and \( y_1 = 2\sqrt{2} \):
\[
y - 2\sqrt{2} = \frac{1}{2\sqrt{2}}(x - 4)
\]Therefore, the equation of the tangent line is:
\[
y = \frac{1}{2\sqrt{2}}x + 2\sqrt{2} - \frac{4}{2\sqrt{2}} = \frac{1}{2\sqrt{2}}x + 2\sqrt{2} - \sqrt{2} = \frac{1}{2\sqrt{2}}x + \sqrt{2}
\]
This example demonstrates how the derivative of \( \sqrt{2x} \) can be used to find the slope of the tangent line to the curve at a specific point.
Derivative of Square Root of 3x
To find the derivative of \( \sqrt{3x} \), we will use the chain rule. The chain rule is particularly useful for finding the derivative of composite functions, where one function is nested within another.
Let's break down the process step by step:
- Identify the outer function and the inner function.
- Apply the chain rule formula: \( (f(g(x)))' = f'(g(x)) \cdot g'(x) \).
For the function \( \sqrt{3x} \), we can identify:
- Outer function: \( f(u) = \sqrt{u} = u^{1/2} \)
- Inner function: \( g(x) = 3x \)
Next, find the derivatives of the outer and inner functions:
- Derivative of the outer function: \( f'(u) = \frac{1}{2} u^{-1/2} = \frac{1}{2\sqrt{u}} \)
- Derivative of the inner function: \( g'(x) = 3 \)
Now, apply the chain rule:
\[
\frac{d}{dx} \sqrt{3x} = \frac{d}{dx} (3x)^{1/2} = \frac{1}{2} (3x)^{-1/2} \cdot 3
\]
Simplify the expression:
\[
\frac{d}{dx} \sqrt{3x} = \frac{1}{2} \cdot \frac{1}{\sqrt{3x}} \cdot 3 = \frac{3}{2\sqrt{3x}}
\]
Therefore, the derivative of \( \sqrt{3x} \) is \( \frac{3}{2\sqrt{3x}} \).
Let's see an example of how this derivative can be used:
Example: Tangent Line to \( \sqrt{3x} \) at \( x = 9 \)
- Find the derivative at \( x = 9 \):
\[
\left. \frac{3}{2\sqrt{3x}} \right|_{x=9} = \frac{3}{2\sqrt{3 \cdot 9}} = \frac{3}{2\sqrt{27}} = \frac{3}{2 \cdot 3\sqrt{3}} = \frac{1}{2\sqrt{3}}
\] - Find the value of the function at \( x = 9 \):
\[
y = \sqrt{3 \cdot 9} = \sqrt{27} = 3\sqrt{3}
\] - Use the point-slope form of the equation of the tangent line:
\[
y - y_1 = m(x - x_1)
\]
where \( m \) is the slope and \( (x_1, y_1) \) is the point of tangency. - Substitute \( m = \frac{1}{2\sqrt{3}} \), \( x_1 = 9 \), and \( y_1 = 3\sqrt{3} \):
\[
y - 3\sqrt{3} = \frac{1}{2\sqrt{3}}(x - 9)
\]Therefore, the equation of the tangent line is:
\[
y = \frac{1}{2\sqrt{3}}x + 3\sqrt{3} - \frac{9}{2\sqrt{3}} = \frac{1}{2\sqrt{3}}x + 3\sqrt{3} - \frac{3\sqrt{3}}{2} = \frac{1}{2\sqrt{3}}x + \frac{3\sqrt{3}}{2}
\]
This example demonstrates how the derivative of \( \sqrt{3x} \) can be used to find the slope of the tangent line to the curve at a specific point.
Common Mistakes and Tips
When finding the derivative of \( \sqrt{x} \) or similar functions, students often make several common mistakes. Here, we will outline these mistakes and provide tips to avoid them.
Common Mistakes
- Forgetting to Apply the Chain Rule
- Incorrectly Simplifying the Derivative
- Missing Negative Signs
- Improper Use of the Power Rule
When differentiating composite functions, such as \( \sqrt{2x} \), it's crucial to use the chain rule. A common error is to treat the function as a simple power of \( x \) and ignore the inner function.
Another common mistake is in the simplification process. Students often forget to correctly simplify expressions involving square roots or fractional exponents.
When dealing with derivatives, especially those involving the chain rule or power rule, missing or misplacing negative signs can lead to incorrect results.
While the power rule is straightforward, errors can occur when applying it to functions with fractional exponents. For instance, the derivative of \( x^{1/2} \) is \( \frac{1}{2}x^{-1/2} \), but students might mistakenly write it as \( \frac{1}{2}x^{1/2} \).
Tips for Success
- Double-Check Your Identification of Inner and Outer Functions
- Practice Simplifying Complex Expressions
- Use Parentheses for Clarity
- Review Fundamental Differentiation Rules
When using the chain rule, ensure that you correctly identify both the inner and outer functions. This step is critical for correctly applying the chain rule.
Spend time practicing the simplification of expressions involving square roots and fractional exponents. This practice will help avoid mistakes in the final steps of finding derivatives.
To avoid missing negative signs or incorrectly grouping terms, use parentheses to clearly delineate parts of your expression.
Regularly review the power rule, chain rule, product rule, and quotient rule to ensure you apply them correctly. Familiarity with these rules will improve your accuracy and efficiency.
Example Problem
Let's work through an example to illustrate common mistakes and how to avoid them.
- Consider the function \( f(x) = \sqrt{3x} \).
- Identify the outer and inner functions:
- Outer function: \( f(u) = \sqrt{u} = u^{1/2} \)
- Inner function: \( g(x) = 3x \)
- Differentiate the outer function: \( f'(u) = \frac{1}{2} u^{-1/2} = \frac{1}{2\sqrt{u}} \).
- Differentiate the inner function: \( g'(x) = 3 \).
- Apply the chain rule: \( \frac{d}{dx} \sqrt{3x} = \frac{1}{2} (3x)^{-1/2} \cdot 3 = \frac{3}{2\sqrt{3x}} \).
By carefully following these steps and avoiding common pitfalls, you can accurately find the derivative of composite functions like \( \sqrt{3x} \).

Conclusion
Understanding the derivative of \( \sqrt{x} \) and similar functions is essential for mastering calculus. Throughout this article, we have explored various methods to find the derivative of \( \sqrt{x} \) and its variations, such as \( \sqrt{2x} \) and \( \sqrt{3x} \), using different rules including the chain rule, product rule, and quotient rule. We also discussed common mistakes and tips to avoid them.
Here are the key takeaways:
- Chain Rule: This rule is crucial when dealing with composite functions. It helps in breaking down the derivative of functions like \( \sqrt{3x} \) into manageable parts.
- Product and Quotient Rules: While these rules are not directly used for \( \sqrt{x} \), they are essential tools in the broader context of differentiation.
- Common Mistakes: Awareness of common pitfalls, such as neglecting the chain rule or incorrectly simplifying derivatives, can significantly improve accuracy.
- Practical Applications: The derivatives of square root functions are widely used in physics, engineering, and economics, making their understanding practically valuable.
By mastering these concepts, students can confidently tackle a wide range of problems involving the differentiation of square root functions and other complex expressions. Practice and careful application of differentiation rules will lead to success in calculus.
In summary, the derivative of \( \sqrt{x} \) is found to be:
\[
\frac{d}{dx} \sqrt{x} = \frac{1}{2\sqrt{x}}
\]
Similarly, for functions like \( \sqrt{2x} \) and \( \sqrt{3x} \), the chain rule helps us find:
\[
\frac{d}{dx} \sqrt{2x} = \frac{1}{\sqrt{2x}}, \quad \frac{d}{dx} \sqrt{3x} = \frac{3}{2\sqrt{3x}}
\]
We hope this comprehensive guide has provided you with a solid understanding of how to differentiate square root functions effectively. Keep practicing and applying these methods to enhance your calculus skills.
Thank you for following along, and happy differentiating!
Cách tìm Đạo hàm của Căn bậc hai x (tức là đạo hàm sqrt x)
READ MORE:
Dẫn xuất của căn bậc hai của x với Quy tắc Lũy thừa | Bài tập Calculus 1
Dẫn xuất căn bậc hai của x với Quy tắc Lũy thừa | Bài tập Calculus 1