Topic square root method calculator: Unlock the power of the square root method calculator with our comprehensive guide. Whether you're simplifying radicals or solving complex equations, this tool will enhance your mathematical prowess. Dive into practical examples, step-by-step instructions, and discover how this calculator can simplify your calculations and boost your confidence in mathematics.
Table of Content
- Square Root Method Calculator
- Introduction to Square Root Method
- Understanding Square Roots
- Types of Square Roots
- Methods for Calculating Square Roots
- Simplifying Square Roots
- Step-by-Step Calculation
- Square Root Calculator Tools
- Examples of Square Root Calculations
- Special Cases in Square Roots
- Applications of Square Roots
- Limitations and Accuracy of Calculations
- FAQs on Square Root Calculations
- Additional Resources and References
- YOUTUBE:
Square Root Method Calculator
The square root method calculator is a useful tool for finding the principal square root and roots of real numbers. Here, you will learn how to use the square root method for various mathematical calculations.
Calculator Use
Use this calculator to find the principal square root and roots of real numbers. Inputs for the radicand \( x \) can be positive or negative real numbers. The answer will also tell you if you entered a perfect square.
The answer will show you the complex or imaginary solutions for square roots of negative real numbers.
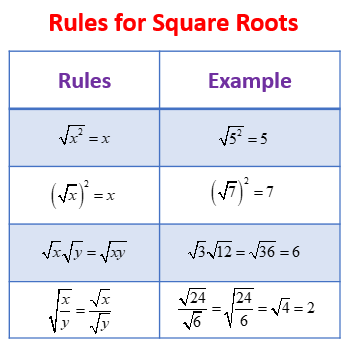
Square Roots: Odd and Even
There are 2 possible roots for any positive real number: a positive root and a negative root. Given a number \( x \), the square root of \( x \) is a number \( a \) such that \( a^{2} = x \). For example, the square roots of 9 are -3 and +3, since \((-3)^{2} = (+3)^{2} = 9\).
Any nonnegative real number \( x \) has a unique nonnegative square root \( r \); this is called the principal square root. For example, the principal square root of 9 is \( \sqrt{9} = +3 \), while the other square root of 9 is \( -\sqrt{9} = -3 \). In common usage, unless otherwise specified, "the" square root is generally taken to mean the principal square root.
Examples of Square Roots
- The 2nd root of 81, or the square root of 81, is written as \( \sqrt[2]{81} = \sqrt[]{81} = \pm 9 \)
- The 2nd root of 25, or the square root of 25, is written as \( \sqrt[2]{25} = \sqrt[]{25} = \pm 5 \)
- The 2nd root of 100, or the square root of 100, is written as \( \sqrt[2]{100} = \sqrt[]{100} = \pm 10 \)
- The 2nd root of 10, or the square root of 10, is written as \( \sqrt[2]{10} = \sqrt[]{10} = \pm 3.162278 \)
Square Root Method for Solving Quadratic Equations
One can also use the square root method to solve quadratic equations. For example, consider the quadratic equation:
\[x^2 - 4 = 0\]
Taking the square root on both sides, we get:
\[x = \pm 2\]
Another example is solving a more complex equation using the square root method:
\[-2x^2 + 15 = x^2 - 12\]
Rearranging and simplifying, we get:
\[3x^2 = 27\]
Taking the square root on both sides, we obtain:
\[x = \pm 3\]
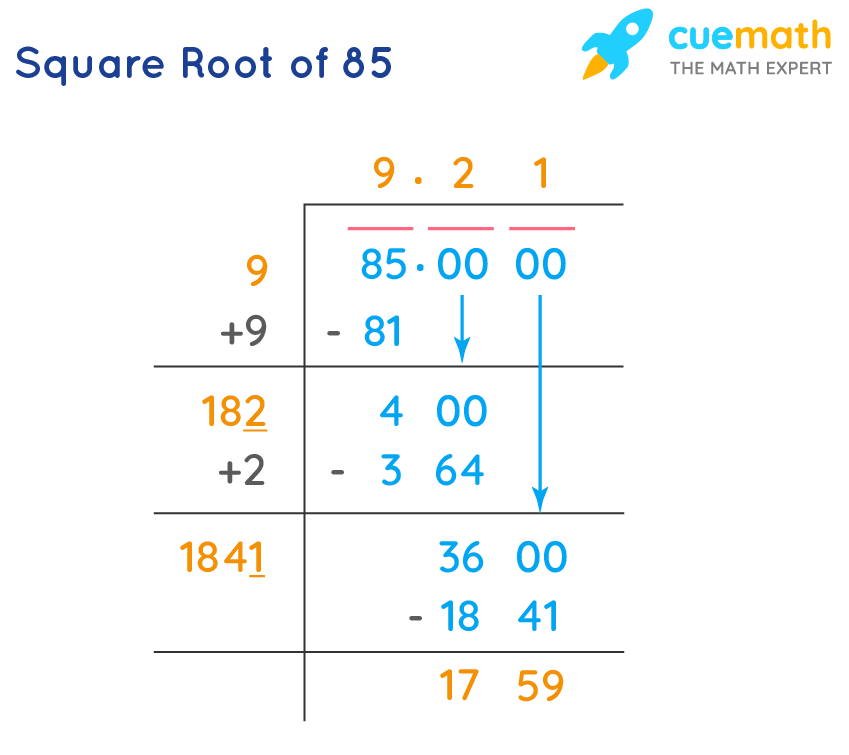
Step-by-Step Instructions Using Division Method
- Group the digits into pairs, from right to left for digits to the left of the decimal point, and from left to right for digits after the decimal point.
- Find the largest number whose square is less than or equal to the number in the leftmost group. Take this number as the divisor and the quotient.
- Bring down the next pair of digits. Add the divisor with the quotient and enter it with a blank on its right.
- Guess the largest possible digit to fill the blank such that the new divisor multiplied by the new quotient is less than or equal to the dividend.
- Continue this process until you reach the desired decimal places.
Example Calculation
To calculate the square root of 5 using the division method:
The square root of 5 = \( \sqrt{5} = 2.236 \)

READ MORE:
Introduction to Square Root Method
The square root method is a mathematical process used to find a number which, when multiplied by itself, equals a given value. This method is essential for various applications in science, engineering, and everyday calculations. Understanding the square root method involves knowing about perfect squares, the principal square root, and different techniques to approximate square roots.
Mathematically, the square root of a number \( x \) is denoted as \( \sqrt{x} \), and it is defined such that \( \sqrt{x} \times \sqrt{x} = x \). For example, the square root of 16 is 4, since \( 4 \times 4 = 16 \). The square root symbol is also known as the radical symbol.
Each positive number has two square roots: one positive (principal square root) and one negative. For instance, the square roots of 9 are 3 and -3, as both \( 3^2 \) and \( (-3)^2 \) equal 9. However, in practical applications, the principal square root is usually considered.
Square roots can be calculated using various methods, including:
- Prime Factorization: Decomposing the number into its prime factors and pairing the factors to find the root.
- Long Division Method: A step-by-step approach to manually finding the square root, useful for precise calculations.
- Babylonian Method: An iterative approximation technique also known as Heron's method.
Here's a simple table to illustrate some perfect squares and their square roots:
| Number | Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
Square roots are not only limited to whole numbers but also include fractions and decimals. For example, the square root of 0.25 is 0.5, since \( 0.5 \times 0.5 = 0.25 \). Complex numbers also come into play for the square roots of negative numbers, introducing imaginary numbers.
Using a square root calculator simplifies the process by automatically performing the necessary calculations, providing both the principal and negative roots, and indicating if the number is a perfect square. This tool is invaluable for students, professionals, and anyone needing quick and accurate square root results.
Understanding Square Roots
Square roots are fundamental concepts in mathematics, often introduced in early education and used extensively in various fields such as engineering, physics, and computer science. Understanding square roots involves comprehending the relationship between a number and its root, the methods to calculate them, and their applications.
The square root of a number \(x\) is a value \(y\) such that \(y \cdot y = x\). This is expressed as \(\sqrt{x} = y\). For example, \(\sqrt{9} = 3\) because \(3 \cdot 3 = 9\).
Properties of Square Roots
- Every positive number has two square roots: one positive and one negative. For instance, \(\sqrt{25} = 5\) and \(-\sqrt{25} = -5\).
- The square root of zero is zero: \(\sqrt{0} = 0\).
- Negative numbers do not have real square roots, as the square of a real number is always non-negative. They have imaginary square roots, represented using the imaginary unit \(i\), where \(i = \sqrt{-1}\).
Methods to Calculate Square Roots
- Long Division Method
- Group the digits into pairs starting from the decimal point.
- Find the largest number whose square is less than or equal to the number in the leftmost group.
- Use this number as the divisor and the quotient. Divide and get the remainder.
- Bring down the next pair of digits and repeat the process.
- Babylonian Method (Heron's Method)
- Guess a starting value \(x_0\) for \(\sqrt{S}\).
- Use the iteration formula: \(x_{n+1} = \frac{1}{2} \left(x_n + \frac{S}{x_n}\right)\).
- Repeat the process until the difference between consecutive values is smaller than a desired tolerance.
- Using a Calculator
- Input the number and use the square root function, usually denoted as \(\sqrt{}\) or a similar symbol.
Applications of Square Roots
- Geometry: Calculating the diagonal of a square, determining distances.
- Physics: In equations involving kinetic energy, wave functions, etc.
- Statistics: Standard deviation calculation, variance analysis.
Example Calculation
Let's calculate the square root of 5 using the long division method:
| 1 | 2 | 2.23 |
| 2 | 05 | 05.00 |
| -4 | 1 | 100 |
| 16 | 2.236 | 271 |
The square root of 5 is approximately \(2.236\).
Conclusion
Square roots are vital in various scientific and mathematical applications. Mastering the calculation methods, understanding their properties, and knowing their practical applications can significantly enhance your mathematical skills and problem-solving abilities.
Types of Square Roots
Square roots can be categorized based on their properties and the type of numbers they operate on. Understanding these types helps in various mathematical and practical applications.
- Perfect Squares: These are numbers whose square roots are integers. For example, the square roots of 4, 9, 16, and 25 are 2, 3, 4, and 5 respectively.
- Non-Perfect Squares: Numbers that do not have integer square roots. Their square roots are irrational numbers. For instance, the square root of 2 is approximately 1.414, which cannot be expressed as a precise fraction.
- Rational Square Roots: When the square root of a number is a rational number. For example, √(1/4) = 1/2.
- Irrational Square Roots: Square roots that result in irrational numbers, which cannot be precisely expressed as fractions. An example is √3, which is approximately 1.732.
- Positive and Negative Square Roots: Each positive real number has two square roots: one positive (principal square root) and one negative. For example, the square roots of 25 are 5 and -5.
- Complex Square Roots: For negative numbers, the square roots are complex numbers. For example, the square roots of -1 are i and -i, where i is the imaginary unit.
Examples of Square Root Calculations
Let's look at some examples to understand the different types of square roots better:
| Number | Square Root | Type |
|---|---|---|
| 4 | ±2 | Perfect Square |
| 2 | ±1.414 | Non-Perfect Square |
| 1/4 | ±1/2 | Rational |
| 3 | ±1.732 | Irrational |
| -1 | ±i | Complex |
Square Roots in Practical Applications
Square roots are widely used in various fields. In geometry, they are essential for calculating distances and areas. For instance, the Pythagorean theorem involves square roots to determine the length of the sides of a right triangle:
In finance, square roots are used in risk management to calculate standard deviations and variances. In engineering, they help in understanding wave functions and signal processing.
Understanding the different types of square roots and their applications can significantly enhance problem-solving skills in mathematics and its related fields.
Methods for Calculating Square Roots
Calculating square roots can be approached using several methods, each with its advantages and specific steps. Here are some common methods:
1. Long Division Method
This traditional method provides high accuracy but can be time-consuming. Here’s a step-by-step process:
- Group the digits into pairs starting from the decimal point.
- Find the largest number whose square is less than or equal to the first group. This is the initial divisor and quotient.
- Subtract the square of the quotient from the first group and bring down the next pair of digits.
- Double the current quotient and use it as the new divisor base. Find a digit to complete the divisor such that the product is less than or equal to the current number.
- Repeat the process until the desired precision is reached.
2. Babylonian Method (Heron's Method)
This iterative method is faster but requires a good initial guess:
- Make an initial guess for the square root.
- Improve the guess using the formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{S}{x_n} \right) \), where \( S \) is the number whose square root is being calculated.
- Repeat the process until the difference between successive guesses is within an acceptable range.
3. Newton's Method
Similar to the Babylonian method, Newton's method uses iterations to refine the estimate:
- Choose an initial estimate \( x_0 \).
- Apply the formula: \( x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \), where \( f(x) = x^2 - S \) and \( f'(x) = 2x \).
- Continue iterating until the value stabilizes.
4. Estimation and Refinement
This quick method is useful for rough estimates:
- Find the nearest perfect squares around the number.
- Estimate the square root based on these values.
- Refine the estimate by averaging or other simple adjustments.
Comparison of Methods
| Method | Advantages | Disadvantages | Accuracy |
|---|---|---|---|
| Long Division | High accuracy | Time-consuming | Very High |
| Babylonian Method | Faster | Less accurate without a good initial guess | Moderate |
| Newton's Method | Quick | Requires good initial guess | High |
| Estimation | Quick and simple | Less precise | Low |
Choosing the appropriate method depends on the required accuracy and the context in which the calculation is performed. Each method provides a unique balance between speed and precision, making them suitable for different applications.

Simplifying Square Roots
Simplifying square roots is an essential skill in mathematics that involves expressing a square root in its simplest form. Here, we'll walk through the step-by-step process of simplifying square roots.
-
Prime Factorization:
Start by finding the prime factors of the number under the square root. Prime factorization involves breaking down the number into its prime components.
- Example: To simplify √72, first find the prime factors of 72.
- 72 = 2 × 2 × 2 × 3 × 3
-
Pairing Prime Factors:
Group the prime factors into pairs. Each pair of identical factors can be taken out from under the square root.
- In our example, 72 = (2 × 2) × (2) × (3 × 3)
- We have pairs: (2 × 2) and (3 × 3)
-
Take Out the Pairs:
Take one number from each pair and multiply them outside the square root.
- √72 = √((2 × 2) × (3 × 3) × 2)
- √72 = 2 × 3 × √2
- So, √72 simplifies to 6√2
By following these steps, you can simplify any square root efficiently. This method helps in making complex calculations more manageable and comprehensible.
Step-by-Step Calculation
Calculating the square root of a number step-by-step involves breaking down the process into manageable steps. Below, we will demonstrate the long division method for finding the square root of a number.
- Preparation: Start by grouping the digits of the number in pairs from the decimal point. For example, to find the square root of 152.2756, group as follows: (15)(22)(75)(60).
- Find the largest square: Identify the largest square number less than or equal to the first group (15). In this case, 32 = 9. Write 3 as the first digit of the root.
- Subtract and bring down: Subtract the square from the first group (15 - 9 = 6). Bring down the next pair (22) to get 622.
- Double the root: Double the current root (3) to get 6. This will be part of the next divisor.
- Find the next digit: Find a digit (x) such that 60x * x is less than or equal to 622. Here, 62 is the closest match (6 * 62 = 372).
- Subtract and repeat: Subtract 372 from 622 to get 250. Bring down the next pair (75) to get 25075. Repeat the process until you have the desired accuracy.
Let's apply this method step-by-step for the number 152.2756:
| Step | Calculation |
|---|---|
| 1 | Group digits: (15)(22)(75)(60) |
| 2 | Find largest square: 32 = 9 |
| 3 | Subtract and bring down: 15 - 9 = 6, bring down 22 to get 622 |
| 4 | Double the root: 3 * 2 = 6 |
| 5 | Find next digit: 6 * 62 = 372, 622 - 372 = 250 |
| 6 | Bring down next pair: 25075 |
Continue this process until you have achieved the desired level of precision. This method ensures a thorough and accurate calculation of square roots.
By using the long division method, you can manually find the square root of any number to the desired decimal place, making it a reliable technique for precise calculations.
Square Root Calculator Tools
Square root calculator tools are valuable resources for quickly and accurately finding the square root of any given number. These tools come with various features to assist both students and professionals in their mathematical calculations. Below is an overview of how to use some popular square root calculator tools:
1. Mathway Square Root Calculator
The Mathway Square Root Calculator allows you to find the square root of any number by simply entering the radical expression. Here's how you can use it:
- Enter the number or expression under the square root symbol.
- Click the blue arrow to submit.
- Select "Calculate the Square Root" from the topic selector.
- View the result, which will be provided in both exact form and decimal form if applicable.
This tool is particularly useful for solving algebra problems and provides step-by-step solutions.
2. Omni Calculator
Omni Calculator simplifies the process of finding square roots by breaking down the number into its factors. To use this calculator:
- Enter the number for which you need to find the square root.
- The calculator will display whether the number is a perfect square and show the simplified form if possible.
- For non-perfect squares, it provides the decimal approximation of the square root.
Omni Calculator also helps in understanding the concept of simplifying square roots by displaying the factors involved.
3. Everyday Calculation Square Root Calculator
This tool offers a detailed step-by-step method for calculating square roots using the division method. Here's how you can use it:
- Enter the positive whole number or decimal.
- The calculator groups the digits into pairs and performs division steps, showing each intermediate result.
- It continues the process until the square root is found up to three decimal places.
The step-by-step approach makes this tool ideal for learning and teaching purposes, as it demonstrates each stage of the calculation.
4. Calculator.io
The Calculator.io tool is versatile and can handle both positive and negative inputs, returning both the principal and negative square roots. To use this calculator:
- Enter the number you want to evaluate.
- Press "Calculate" to see the principal and opposite square roots.
- The calculator will also indicate if the number is a perfect square.
This tool is particularly useful for comprehensive understanding and includes additional explanations about squares and square roots, perfect squares, and more.
These tools are user-friendly and provide quick, accurate results, making them essential for anyone dealing with square root calculations.
Examples of Square Root Calculations
Understanding how to calculate square roots is essential for solving various mathematical problems. Here are some examples demonstrating different methods for calculating square roots.
Example 1: Calculating the Square Root of 16
The square root of 16 is calculated as follows:
- \(\sqrt{16} = 4\)
This is because \(4 \times 4 = 16\).
Example 2: Calculating the Square Root of a Non-Perfect Square (e.g., 20)
For non-perfect squares, you can use the approximation method:
- Find two perfect squares between which the number lies. For 20, it is between 16 (\(4^2\)) and 25 (\(5^2\)).
- Approximate the square root: \(\sqrt{20}\) is between 4 and 5.
- Refine the approximation: \(\sqrt{20} \approx 4.47\).
Example 3: Using the Prime Factorization Method (e.g., 72)
Prime factorize the number and simplify:
- Prime factorization of 72: \(72 = 2^3 \times 3^2\).
- Simplify: \(\sqrt{72} = \sqrt{2^3 \times 3^2} = \sqrt{(2^2 \times 2) \times 3^2} = \sqrt{2^2} \times \sqrt{3^2} \times \sqrt{2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}\).
So, \(\sqrt{72} = 6\sqrt{2}\).
Example 4: Calculating the Square Root of a Decimal (e.g., 0.64)
To find the square root of a decimal:
- \(\sqrt{0.64} = 0.8\)
This is because \(0.8 \times 0.8 = 0.64\).
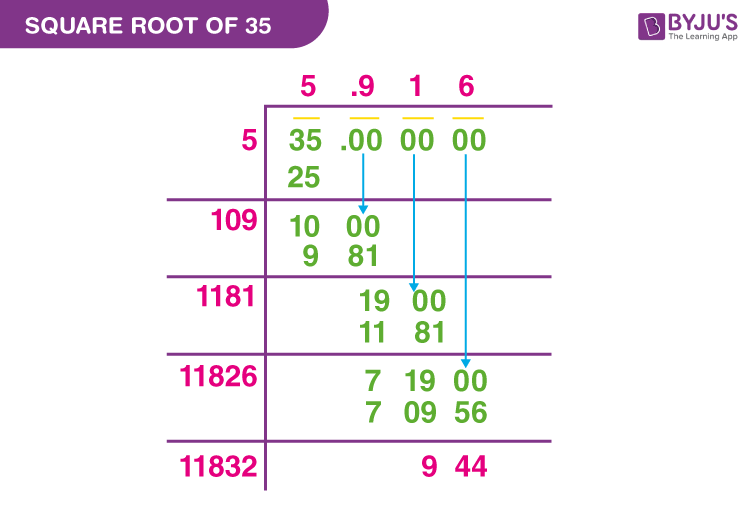
Example 5: Using the Long Division Method (e.g., 45)
The long division method for finding square roots is a step-by-step process:
- Pair the digits from right to left. For 45, it's 45.
- Find the largest number whose square is less than or equal to the first pair. Here, it's 6 (since \(6^2 = 36\) and \(7^2 = 49\)).
- Subtract the square of this number from the first pair and bring down the next pair of digits. Continue this process.
- Approximation: \(\sqrt{45} \approx 6.7\).
Example 6: Calculating the Square Root Using a Calculator
Modern calculators simplify the process of finding square roots. For instance, to find \(\sqrt{81}\):
- Enter 81 into the calculator.
- Press the square root (√) button.
- The result is \( \sqrt{81} = 9 \).
These examples demonstrate various methods for calculating square roots, from simple mental math to more complex techniques suitable for non-perfect squares and decimals.
Special Cases in Square Roots
Square roots have several special cases that are important to understand for thorough comprehension of this mathematical concept. These cases include perfect squares, imaginary numbers, and non-perfect squares.
Perfect Squares
A perfect square is a number that has an integer as its square root. For instance:
- The square root of \(16\) is \(4\), because \(4 \times 4 = 16\).
- The square root of \(81\) is \(9\), because \(9 \times 9 = 81\).
- The square root of \(100\) is \(10\), because \(10 \times 10 = 100\).
In mathematical notation:
\(\sqrt{16} = 4\)
\(\sqrt{81} = 9\)
\(\sqrt{100} = 10\)
Imaginary Numbers
When dealing with the square roots of negative numbers, the result is an imaginary number. The basic imaginary unit is denoted as \(i\), where \(i = \sqrt{-1}\). For example:
- The square root of \(-4\) is \(2i\), because \((2i) \times (2i) = -4\).
- The square root of \(-9\) is \(3i\), because \((3i) \times (3i) = -9\).
In mathematical notation:
\(\sqrt{-4} = 2i\)
\(\sqrt{-9} = 3i\)
Non-Perfect Squares
For numbers that are not perfect squares, their square roots are irrational numbers, often expressed in decimal form. These numbers cannot be expressed as a fraction and have non-repeating, non-terminating decimal expansions. For example:
- The square root of \(10\) is approximately \(3.162\), because \(3.162 \times 3.162 \approx 10\).
- The square root of \(2\) is approximately \(1.414\), because \(1.414 \times 1.414 \approx 2\).
In mathematical notation:
\(\sqrt{10} \approx 3.162\)
\(\sqrt{2} \approx 1.414\)
Summary Table
| Number | Square Root | Type |
|---|---|---|
| 16 | 4 | Perfect Square |
| -4 | 2i | Imaginary Number |
| 10 | 3.162 | Non-Perfect Square |
Understanding these special cases in square roots helps in solving various mathematical problems and recognizing the different types of results that can be expected when calculating square roots.
Applications of Square Roots
Square roots have a wide range of applications in various fields. Understanding these applications can provide insight into their importance and practical utility. Here are some common applications:
-
Geometry and Trigonometry:
Square roots are crucial in geometry for calculating distances and lengths. For instance, in the Pythagorean theorem, the length of the hypotenuse \( c \) of a right triangle is given by \( c = \sqrt{a^2 + b^2} \), where \( a \) and \( b \) are the lengths of the other two sides.
-
Physics:
In physics, square roots are used in formulas involving waves and oscillations. For example, the period \( T \) of a simple pendulum is given by \( T = 2\pi\sqrt{\frac{L}{g}} \), where \( L \) is the length of the pendulum and \( g \) is the acceleration due to gravity.
-
Statistics:
Square roots are used to compute standard deviation, which is a measure of the amount of variation or dispersion in a set of values. The standard deviation \( \sigma \) is calculated as \( \sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2} \), where \( N \) is the number of values, \( x_i \) is each individual value, and \( \mu \) is the mean of the values.
-
Engineering:
In engineering, square roots are used in various calculations, such as determining the RMS (root mean square) value of an alternating current (AC) signal. The RMS value is given by \( V_{RMS} = \sqrt{\frac{1}{T}\int_0^T v(t)^2 \, dt} \), where \( v(t) \) is the instantaneous voltage and \( T \) is the period.
-
Finance:
Square roots are used in finance to calculate the volatility of an asset, which is often measured as the standard deviation of its returns. Volatility \( \sigma \) is given by \( \sigma = \sqrt{\frac{1}{N-1}\sum_{i=1}^{N}(R_i - \bar{R})^2} \), where \( R_i \) are the individual returns and \( \bar{R} \) is the average return.
Square roots also appear in many other fields, including biology, chemistry, and computer science, demonstrating their broad applicability and essential role in various scientific and practical contexts.
Limitations and Accuracy of Calculations
When calculating square roots, various methods and tools can lead to different degrees of accuracy and limitations. Understanding these aspects is crucial for accurate and reliable results.
Limitations of Square Root Calculations
- Precision of Calculators: Most calculators and software are limited by their floating-point precision. This can lead to small rounding errors, especially for very large or very small numbers.
- Manual Calculation Errors: Methods like long division or approximation can introduce human errors, especially in complex calculations.
- Perfect Squares: When dealing with non-perfect squares, the results are often irrational numbers that cannot be expressed exactly, leading to approximations.
- Negative Numbers: Calculating square roots of negative numbers involves imaginary numbers, which are not handled by standard real-number calculators.
Accuracy of Different Methods
Different methods of calculating square roots have varying levels of accuracy:
- Long Division Method: This method is precise but can be time-consuming and prone to human error if not performed carefully.
- Newton's Method: An iterative approach that converges quickly to a high-precision result. It's widely used in computer algorithms due to its efficiency.
- Calculator Tools: Modern calculators and software often use advanced algorithms to provide highly accurate results, but they are still subject to the precision limits of their floating-point arithmetic.
Improving Accuracy
To achieve more accurate results, consider the following steps:
- Use Reputable Tools: Online calculators from trusted sources often use high-precision algorithms.
- Verify Results: Cross-check results using different methods or tools to ensure consistency.
- Understand Limitations: Be aware of the limitations of your chosen method and account for potential errors in your calculations.
Example Calculation
Let's calculate the square root of 2 using Newton's Method:
- Start with an initial guess, \( x_0 = 1 \).
- Apply the iteration formula: \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{2}{x_n} \right) \).
- Continue iterating until the desired precision is reached:
- Iteration 1: \( x_1 = \frac{1}{2} \left( 1 + \frac{2}{1} \right) = 1.5 \)
- Iteration 2: \( x_2 = \frac{1}{2} \left( 1.5 + \frac{2}{1.5} \right) \approx 1.4167 \)
- Iteration 3: \( x_3 = \frac{1}{2} \left( 1.4167 + \frac{2}{1.4167} \right) \approx 1.4142 \)
- The result converges to approximately 1.4142, which is a good approximation of \( \sqrt{2} \).
By understanding the limitations and accuracy of different methods, you can choose the best approach for your needs and ensure precise and reliable square root calculations.
FAQs on Square Root Calculations
Below are some frequently asked questions about square root calculations:
-
What is a square root?
The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 16 is 4 because 4 × 4 = 16.
-
How do you find the square root of a number?
There are several methods to find the square root, including the prime factorization method, the long division method, and using a calculator. For example, using the long division method, you can find the square root of a number by dividing it into pairs of digits starting from the decimal point.
-
What is the principal square root?
The principal square root is the non-negative root of a number. For example, the principal square root of 9 is 3, even though -3 is also a square root of 9.
-
Can negative numbers have real square roots?
No, negative numbers do not have real square roots. The square root of a negative number is an imaginary number. For example, the square root of -1 is represented as i, where i is the imaginary unit.
-
How are square roots used in real life?
Square roots are used in various fields such as engineering, physics, and finance. For instance, they are used in calculating areas, solving quadratic equations, and in algorithms for computer science.
-
What is a perfect square?
A perfect square is a number that is the square of an integer. For example, 1, 4, 9, and 16 are perfect squares because they can be written as 12, 22, 32, and 42 respectively.
-
How can I simplify square roots?
To simplify a square root, you need to factor the number into its prime factors and then pair the prime factors. For example, to simplify √18, you can factor it into √(9×2) = 3√2.
-
What are some common methods for calculating square roots?
Common methods include the approximation method, using square root tables, and iterative algorithms such as the Newton-Raphson method. Calculators also provide a quick and accurate way to find square roots.
-
Are there any tools available for calculating square roots?
Yes, there are various online tools and calculators available that can compute the square root of any number. These tools can handle both real and imaginary numbers, and provide step-by-step solutions.

Additional Resources and References
For further exploration and deeper understanding of square roots and their calculations, consider the following resources:
-
An online tool that calculates square roots step-by-step, providing exact and decimal forms. It also offers additional algebraic tools for comprehensive mathematical learning.
-
This calculator simplifies square roots and provides detailed explanations of the simplification process. It also includes other mathematical calculators and educational articles.
-
Offers a free calculator to reduce square roots to their simplest radical form, along with worksheets and further reading on simplifying radicals.
-
Provides a straightforward calculator for finding square roots and includes educational content on various methods of calculating and understanding square roots.
-
A resource for comprehensive information on mathematical standards, including square root calculations and their applications in various fields.
-
Offers in-depth courses and resources on advanced mathematics, including detailed studies on the properties and calculations of square roots.
Hướng dẫn sử dụng máy tính 9: Tính căn bậc hai trên máy tính khoa học
READ MORE:
Cách Tính Căn Bậc Hai - Những Con Số Thay Đổi Toán Học Mãi Mãi