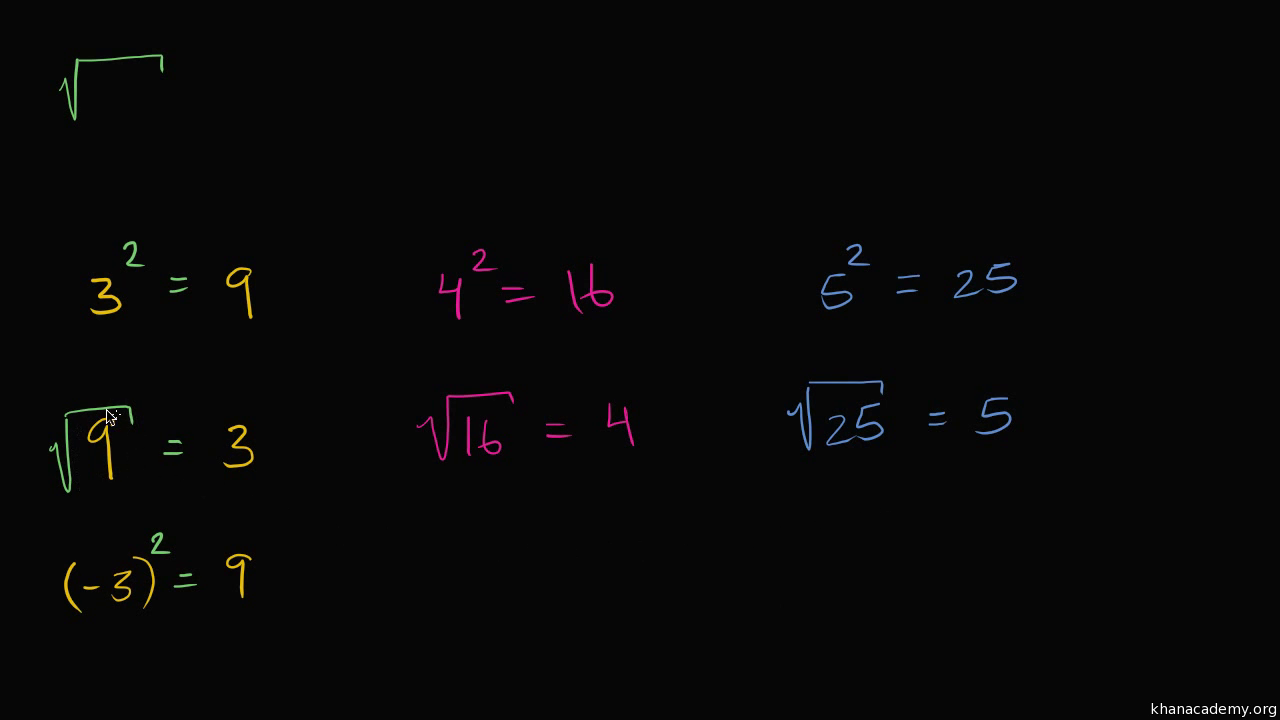Topic square root n: Discover the fascinating world of the square root of \( n \). This guide explores its definition, properties, calculation methods, and wide-ranging applications in mathematics, physics, engineering, and computer science. Whether you're a student or a professional, this article will enhance your understanding and appreciation of this fundamental mathematical concept.
Table of Content
- Understanding the Square Root of n
- Introduction to Square Roots
- Definition and Notation of Square Roots
- Methods for Calculating Square Roots
- Manual Calculation Techniques
- Approximation Methods
- Using Technology to Find Square Roots
- Examples of Square Roots
- Applications of Square Roots
- Square Roots in Mathematics
- Square Roots in Physics
- Square Roots in Engineering
- Square Roots in Computer Science
- Square Roots of Negative Numbers
- Imaginary Numbers and Their Properties
- Advanced Topics in Square Roots
- Square Root Functions and Graphs
- Solving Equations Involving Square Roots
- Square Root Transformations
- YOUTUBE: Khám phá lý thuyết chứng minh căn bậc hai của bất kỳ số nguyên nào là vô tỉ, ngoại trừ các số chính phương.
Understanding the Square Root of n
The square root of a number \( n \) is a value that, when multiplied by itself, gives the number \( n \). It is often represented using the radical symbol \(\sqrt{}\). In mathematical notation, the square root of \( n \) is written as \(\sqrt{n}\).
Definition
If \( x \) is the square root of \( n \), then \( x \) satisfies the equation:
\[ x^2 = n \]
This implies that \( x = \sqrt{n} \).
Properties of Square Roots
- The square root of a positive number is always positive.
- The square root of 0 is 0: \(\sqrt{0} = 0\).
- Negative numbers do not have real square roots, but they have complex square roots.
Square Root Function
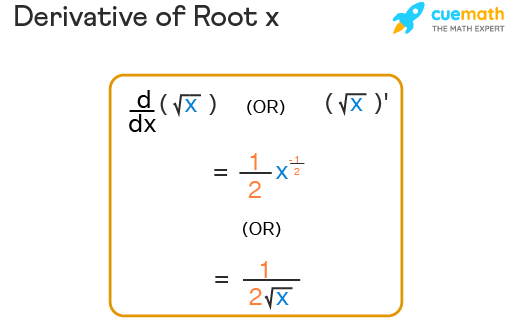
The square root function \( f(x) = \sqrt{x} \) maps a non-negative real number \( x \) to its non-negative square root. This function is continuous and differentiable for all \( x \geq 0 \).
Calculating Square Roots
There are various methods to calculate the square root of a number:
- Using a calculator or computer software.
- Using the long division method for manual calculation.
- Approximating using iterative methods such as the Newton-Raphson method.
Examples
Here are a few examples of square roots:
| \(\sqrt{4}\) | 2 |
| \(\sqrt{9}\) | 3 |
| \(\sqrt{16}\) | 4 |
| \(\sqrt{25}\) | 5 |
Applications
The concept of square roots is widely used in various fields such as:
- Mathematics: Solving quadratic equations and inequalities.
- Physics: Determining the magnitude of vectors and solving kinematic equations.
- Engineering: Calculating stresses and strains in materials.
- Computer Science: Algorithms involving geometric computations.
Complex Square Roots
For negative numbers, the square roots are complex numbers. For example:
\[ \sqrt{-1} = i \]
where \( i \) is the imaginary unit. The general form for the square root of a negative number is:
\[ \sqrt{-n} = \sqrt{n} \cdot i \]
Conclusion
Understanding the square root function is fundamental in mathematics and its applications. It helps in solving various mathematical problems and is a crucial concept in advanced scientific computations.

READ MORE:
Introduction to Square Roots
The square root of a number \( n \) is a value that, when multiplied by itself, yields \( n \). It is represented by the symbol \(\sqrt{}\). For example, the square root of 16 is 4 because \( 4 \times 4 = 16 \).
Understanding square roots is fundamental in mathematics as they appear in various equations and real-world applications. Let's explore this concept step by step.
Basic Definition
If \( x \) is the square root of \( n \), then:
\[ x^2 = n \]
This means that \( x = \sqrt{n} \).
Properties of Square Roots
- The square root of a positive number is always positive or zero.
- The square root of zero is zero: \(\sqrt{0} = 0\).
- Negative numbers do not have real square roots but have complex roots.
Calculating Square Roots
There are several methods to calculate square roots:
- Using a Calculator: The easiest way to find square roots.
- Long Division Method: A manual technique to approximate square roots.
- Newton-Raphson Method: An iterative approach to find increasingly accurate approximations.
Examples
Here are a few common examples of square roots:
| \(\sqrt{4}\) | 2 |
| \(\sqrt{9}\) | 3 |
| \(\sqrt{16}\) | 4 |
| \(\sqrt{25}\) | 5 |
Applications
Square roots are used in various fields:
- Mathematics: Solving quadratic equations and inequalities.
- Physics: Calculating the magnitude of vectors.
- Engineering: Stress and strain calculations in materials.
- Computer Science: Algorithms for geometric computations.
Complex Square Roots
For negative numbers, square roots are complex:
\[ \sqrt{-1} = i \]
where \( i \) is the imaginary unit. The square root of a negative number is:
\[ \sqrt{-n} = \sqrt{n} \cdot i \]
This introduces a new set of numbers called complex numbers, which are essential in advanced mathematics and engineering.
In summary, understanding the square root of \( n \) is crucial in mathematics and its practical applications. By exploring its properties, methods of calculation, and examples, we gain a deeper appreciation for this fundamental concept.
Definition and Notation of Square Roots
The square root of a number \( n \) is a value that, when multiplied by itself, equals \( n \). This fundamental concept is denoted by the radical symbol \(\sqrt{}\) and can be expressed mathematically as:
\[ \sqrt{n} = x \]
where \( x \) is the number that satisfies the equation:
\[ x^2 = n \]
Notation
The square root of \( n \) can be written in several forms:
- Radical Form: \(\sqrt{n}\)
- Exponential Form: \( n^{\frac{1}{2}} \)
Both notations are widely used in mathematical expressions and equations.
Principal Square Root
The principal square root of a non-negative number \( n \) is the non-negative value of \( x \) that satisfies \( x^2 = n \). For example, the principal square root of 25 is 5 because:
\[ 5^2 = 25 \]
Negative Numbers and Complex Roots
Negative numbers do not have real square roots because no real number squared equals a negative number. However, they do have complex roots. The square root of a negative number is defined using the imaginary unit \( i \), where \( i = \sqrt{-1} \). For example:
\[ \sqrt{-9} = 3i \]
where \( i \) is the imaginary unit.
Properties of Square Roots
- \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) for any non-negative numbers \( a \) and \( b \).
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) for any non-negative numbers \( a \) and \( b \), with \( b \neq 0 \).
- \((\sqrt{a})^2 = a\) for any non-negative number \( a \).
Examples
Here are a few examples to illustrate the concept:
| \(\sqrt{1}\) | 1 |
| \(\sqrt{4}\) | 2 |
| \(\sqrt{9}\) | 3 |
| \(\sqrt{16}\) | 4 |
| \(\sqrt{25}\) | 5 |
Understanding the definition and notation of square roots is essential for solving mathematical problems and understanding more advanced concepts in algebra and calculus. Square roots are not only a fundamental aspect of number theory but also play a crucial role in various practical applications across different fields.
Methods for Calculating Square Roots
Calculating square roots can be accomplished using various methods, ranging from simple manual techniques to more advanced algorithms. Here, we explore several common methods for finding the square root of a number \( n \).
1. Using a Calculator
The most straightforward way to find the square root of a number is to use a calculator. Most scientific and graphing calculators have a square root function, typically represented by the symbol \(\sqrt{}\). To find \(\sqrt{n}\), simply enter the number and press the square root button.
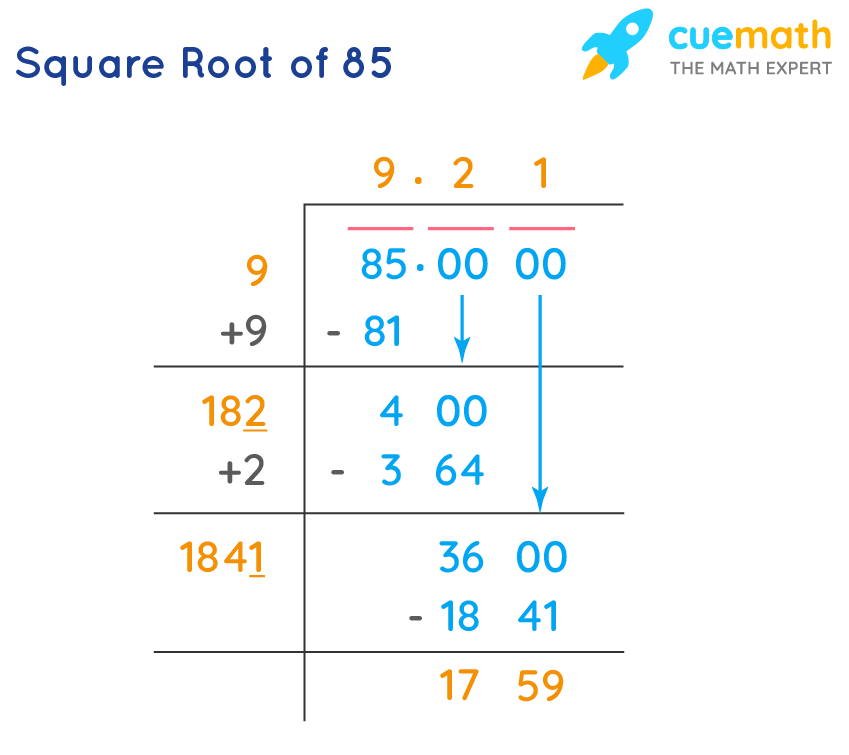
2. Long Division Method
The long division method is a manual technique for finding square roots, which involves a step-by-step approach to approximate the value. Here’s how it works:
- Set up the number: Write the number \( n \) in pairs of digits from the decimal point, both left and right.
- Find the largest square: Identify the largest integer whose square is less than or equal to the leftmost pair or single digit.
- Subtract and bring down: Subtract the square of this integer from the pair and bring down the next pair of digits.
- Double the divisor: Double the current result and find the next digit of the quotient such that the product of the new divisor and the digit is less than or equal to the current remainder.
- Repeat: Continue the process until the desired accuracy is achieved.
3. Newton-Raphson Method
The Newton-Raphson method is an iterative technique for finding increasingly accurate approximations of square roots. The formula for the iteration is:
\[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{n}{x_n} \right) \]
Here’s a step-by-step guide:
- Choose an initial guess \( x_0 \).
- Apply the iteration formula to find the next approximation \( x_1 \).
- Repeat the process until the change between successive approximations is smaller than a predetermined threshold.
4. Estimation and Refinement
This method involves making an initial estimate and refining it through simple arithmetic operations. For example:
- Estimate: Find two perfect squares between which the number \( n \) lies. For instance, if \( n = 10 \), it lies between \( 3^2 = 9 \) and \( 4^2 = 16 \).
- Average: Take the average of these two numbers as the initial estimate. In this case, \( (3 + 4)/2 = 3.5 \).
- Refine: Use the average to find a closer approximation, and repeat if necessary.
Examples
Let's look at examples using some of these methods:
| \(\sqrt{25}\) using a calculator | 5 |
| \(\sqrt{2}\) using the Newton-Raphson method with \( x_0 = 1 \) | Approx. 1.414 |
| \(\sqrt{50}\) using estimation | Approx. 7.071 |
Understanding these methods not only helps in accurately calculating square roots but also enhances problem-solving skills in mathematics. Each method has its own advantages and is suitable for different situations, ranging from quick estimations to high-precision calculations.
Manual Calculation Techniques
While calculators and computers make it easy to find the square root of a number, there are several manual techniques that can be used to calculate square roots. These methods are valuable for understanding the underlying mathematics and can be useful in situations where technology is not available.
1. Long Division Method
The long division method is a step-by-step approach to approximate the square root of a number. Here’s how it works:
- Set up the number: Write the number \( n \) in pairs of digits from the decimal point, both to the left and right.
- Find the largest square: Identify the largest integer whose square is less than or equal to the leftmost pair or single digit.
- Subtract and bring down: Subtract the square of this integer from the pair and bring down the next pair of digits.
- Double the divisor: Double the current result and determine the next digit of the quotient such that the product of the new divisor and the digit is less than or equal to the current remainder.
- Repeat: Continue the process until the desired level of accuracy is achieved.
Example:
To find \(\sqrt{529}\) using the long division method:
- 529 is written as 5 29.
- The largest square less than 5 is 2 (since \(2^2 = 4\)).
- Subtract 4 from 5 to get 1, and bring down 29 to get 129.
- Double 2 to get 4. Find the largest digit \(d\) such that \(4d \times d \leq 129\). Here, \(d = 3\) (since \(43 \times 3 = 129\)).
- Thus, \(\sqrt{529} = 23\).
2. Estimation and Refinement
This technique involves making an initial estimate and refining it through simple arithmetic operations. Here’s a step-by-step guide:
- Estimate: Find two perfect squares between which the number \( n \) lies. For example, for \( n = 20 \), it lies between \(4^2 = 16\) and \(5^2 = 25\).
- Averaging: Take the average of these two numbers as the initial estimate. For \( n = 20 \), the average of 4 and 5 is 4.5.
- Refine: Improve the estimate by averaging 4.5 and \( \frac{20}{4.5} \). Repeat until the desired accuracy is achieved.
Example:
To find \(\sqrt{20}\) using estimation and refinement:
- \(20\) lies between \(16\) and \(25\) (i.e., between \(4^2\) and \(5^2\)).
- Initial estimate: \(\frac{4 + 5}{2} = 4.5\).
- Refinement: \(\frac{4.5 + \frac{20}{4.5}}{2} = \frac{4.5 + 4.444}{2} = 4.472\).
- Further refinement yields \(\sqrt{20} \approx 4.472\).
3. Prime Factorization
This method involves breaking down the number into its prime factors and pairing them to find the square root. Here’s the process:
- Factorize: Find the prime factorization of the number \( n \).
- Pair the factors: Pair the prime factors into groups of two.
- Multiply: Take one number from each pair and multiply them to get the square root.
Example:
To find \(\sqrt{144}\) using prime factorization:
- Prime factorization of 144: \(144 = 2^4 \times 3^2\).
- Pair the factors: \(2^4\) pairs into \(2^2 \times 2^2\) and \(3^2\) pairs into \(3 \times 3\).
- Take one number from each pair: \(2 \times 3 = 6\).
- Thus, \(\sqrt{144} = 12\).
These manual techniques for calculating square roots are not only useful for developing a deeper understanding of the concept but also for enhancing problem-solving skills. Whether using the long division method, estimation and refinement, or prime factorization, each approach offers a unique way to explore the mathematics behind square roots.

Approximation Methods
Approximating square roots is useful when an exact value is not required or when a quick estimate is needed. There are several methods for approximating square roots that range from simple to more complex techniques. Below, we explore some common approximation methods in detail.
1. Estimation Method
The estimation method involves finding two perfect squares between which the number \( n \) lies and then interpolating between them. Here’s a step-by-step guide:
- Identify bounds: Find two perfect squares, \(a^2\) and \(b^2\), such that \(a^2 \leq n \leq b^2\).
- Initial estimate: Use the average of \(a\) and \(b\) as the initial estimate: \[ x_0 = \frac{a + b}{2} \]
- Refine: Adjust the estimate by considering the proximity of \( n \) to \( a^2 \) and \( b^2 \).
Example:
To approximate \(\sqrt{10}\):
- Find bounds: \(3^2 = 9\) and \(4^2 = 16\).
- Initial estimate: \( \frac{3 + 4}{2} = 3.5 \).
- Refine: Since 10 is closer to 9 than 16, adjust the estimate slightly downward, giving \( \sqrt{10} \approx 3.2 \).
2. Newton-Raphson Method
The Newton-Raphson method is an iterative technique that provides increasingly accurate approximations. The formula for the iteration is:
\[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{n}{x_n} \right) \]
Here’s how to apply it:
- Choose an initial guess: Start with an initial guess \( x_0 \).
- Apply the iteration: Use the formula to compute the next approximation \( x_1 \).
- Repeat: Continue iterating until the desired accuracy is achieved.
Example:
To approximate \(\sqrt{2}\):
- Initial guess: \( x_0 = 1 \).
- First iteration: \[ x_1 = \frac{1}{2} \left( 1 + \frac{2}{1} \right) = 1.5 \]
- Second iteration: \[ x_2 = \frac{1}{2} \left( 1.5 + \frac{2}{1.5} \right) \approx 1.4167 \]
- Further iterations yield more accurate approximations, with \(\sqrt{2} \approx 1.414\).
3. Babylonian Method
The Babylonian method, also known as Heron's method, is an ancient algorithm similar to the Newton-Raphson method. The iterative formula is:
\[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{n}{x_n} \right) \]
It works as follows:
- Initial guess: Start with an initial guess \( x_0 \).
- Iterate: Apply the formula to get the next approximation \( x_1 \).
- Repeat: Continue iterating until the change between successive approximations is negligible.
Example:
To approximate \(\sqrt{50}\):
- Initial guess: \( x_0 = 7 \) (since \( 7^2 = 49 \)).
- First iteration: \[ x_1 = \frac{1}{2} \left( 7 + \frac{50}{7} \right) \approx 7.071 \]
- Second iteration: \[ x_2 = \frac{1}{2} \left( 7.071 + \frac{50}{7.071} \right) \approx 7.071 \]
- Further iterations confirm that \(\sqrt{50} \approx 7.071\).
4. Linear Approximation
Linear approximation uses the tangent line at a known point to estimate the square root of nearby values. For small changes \( \Delta x \), the approximation is:
\[ \sqrt{a + \Delta x} \approx \sqrt{a} + \frac{\Delta x}{2\sqrt{a}} \]
Example:
To approximate \(\sqrt{10}\) using \(\sqrt{9} = 3\):
- Identify \( a \): \( a = 9 \).
- Calculate \( \Delta x \): \( \Delta x = 1 \).
- Apply the formula: \[ \sqrt{10} \approx 3 + \frac{1}{2 \times 3} = 3 + \frac{1}{6} \approx 3.167 \]
These approximation methods provide valuable tools for quickly estimating square roots with varying degrees of accuracy. Understanding and applying these techniques can enhance problem-solving skills and deepen comprehension of numerical methods in mathematics.
Using Technology to Find Square Roots
Technology has made it incredibly easy to find the square root of a number. Various tools, from basic calculators to advanced software, provide quick and accurate results. Here, we explore several technological methods to find square roots.
1. Using a Calculator
Most calculators, including basic, scientific, and graphing calculators, have a dedicated square root function. Here’s how to use them:
- Basic Calculator: Enter the number \( n \) and press the square root button (\(\sqrt{}\)).
- Scientific Calculator: Enter the number \( n \), press the \(\sqrt{}\) button, or use the secondary function key followed by the square root symbol.
- Graphing Calculator: Similar to scientific calculators, enter the number and press the square root function key or access it through the function menu.
Example:
To find \(\sqrt{25}\) using a calculator, simply enter 25 and press the square root button to get 5.
2. Using Spreadsheet Software
Spreadsheet software like Microsoft Excel, Google Sheets, and others can calculate square roots using built-in functions. Here’s a step-by-step guide:
- Open the software: Launch Excel or Google Sheets.
- Enter the number: Type the number \( n \) in a cell.
- Use the SQRT function: In another cell, type the formula \( =SQRT(cell\_reference) \). For example, if the number is in cell A1, type \( =SQRT(A1) \).
- Press Enter: The cell will display the square root of the number.
Example:
To find \(\sqrt{16}\) in Excel:
- Enter 16 in cell A1.
- In cell B1, type \( =SQRT(A1) \).
- Press Enter to get 4.
3. Using Online Calculators
Many websites offer free online calculators that can compute square roots instantly. Here’s how to use them:
- Search for an online calculator: Use keywords like "square root calculator" in your search engine.
- Enter the number: Type the number \( n \) into the input box.
- Calculate: Click the calculate button or press Enter to see the result.
Example:
To find \(\sqrt{81}\) using an online calculator, simply enter 81 in the input field and press the calculate button to get 9.
4. Using Programming Languages
Programming languages like Python, Java, and C++ have built-in functions to calculate square roots. Here’s how to do it in Python:
- Install Python: Ensure Python is installed on your computer.
- Write the code: Open a text editor or IDE and write the following code:
import math n = 49 sqrt_n = math.sqrt(n) print("The square root of", n, "is", sqrt_n) - Run the code: Save the file and run it in the terminal or command prompt.
Example:
Running the above code will output: "The square root of 49 is 7.0".
5. Using Mobile Apps
Many mobile apps, available for both Android and iOS, can calculate square roots. Here’s how to use them:
- Download an app: Search for and download a calculator app from the App Store or Google Play.
- Open the app: Launch the app on your device.
- Enter the number: Input the number \( n \) using the keypad.
- Calculate: Press the square root button to get the result.
Example:
To find \(\sqrt{100}\) using a mobile app, open the app, enter 100, and press the square root button to get 10.
Using technology to find square roots simplifies the process and ensures accuracy. Whether using a calculator, spreadsheet, online tool, programming language, or mobile app, these methods provide quick and reliable results.
Examples of Square Roots
The square root of a number \( n \) is a value that, when multiplied by itself, gives \( n \). Below are some examples of square roots for various types of numbers:
Square Roots of Perfect Squares
- \(\sqrt{1} = 1\)
- \(\sqrt{4} = 2\)
- \(\sqrt{9} = 3\)
- \(\sqrt{16} = 4\)
- \(\sqrt{25} = 5\)
- \(\sqrt{36} = 6\)
- \(\sqrt{49} = 7\)
- \(\sqrt{64} = 8\)
- \(\sqrt{81} = 9\)
- \(\sqrt{100} = 10
Square Roots of Non-Perfect Squares
For numbers that are not perfect squares, the square roots are irrational numbers:
- \(\sqrt{2} \approx 1.414\)
- \(\sqrt{3} \approx 1.732\)
- \(\sqrt{5} \approx 2.236\)
- \(\sqrt{6} \approx 2.449\)
- \(\sqrt{7} \approx 2.646\)
- \(\sqrt{8} \approx 2.828\)
- \(\sqrt{10} \approx 3.162\)
Square Roots of Fractions
Square roots can also be calculated for fractions:
- \(\sqrt{\frac{1}{4}} = \frac{1}{2}\)
- \(\sqrt{\frac{1}{9}} = \frac{1}{3}\)
- \(\sqrt{\frac{1}{16}} = \frac{1}{4}\)
- \(\sqrt{\frac{1}{25}} = \frac{1}{5}\)
Square Roots of Decimals
Calculating the square root of decimals follows the same principle:
- \(\sqrt{0.01} = 0.1\)
- \(\sqrt{0.04} = 0.2\)
- \(\sqrt{0.09} = 0.3\)
- \(\sqrt{0.16} = 0.4\)
Square Roots of Large Numbers
Square roots can also be found for large numbers, often using technology or approximation methods:
- \(\sqrt{144} = 12\)
- \(\sqrt{256} = 16\)
- \(\sqrt{625} = 25\)
- \(\sqrt{1024} = 32\)
Summary Table of Square Roots
| Number (n) | Square Root (\(\sqrt{n}\)) |
|---|---|
| 1 | 1 |
| 2 | \(\approx 1.414\) |
| 3 | \(\approx 1.732\) |
| 4 | 2 |
| 5 | \(\approx 2.236\) |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
Applications of Square Roots
Square roots are utilized in various fields and applications, making them essential in both theoretical and practical contexts. Below are some key applications of square roots:
-
Geometry
In geometry, square roots are used to calculate the length of the sides of squares and right triangles. For example, the length of the diagonal of a square with side length \( a \) is given by \( \sqrt{2}a \). Similarly, the Pythagorean theorem uses square roots to find the length of a side in right triangles.
The formula is: \( c = \sqrt{a^2 + b^2} \), where \( c \) is the hypotenuse, and \( a \) and \( b \) are the other two sides.
-
Physics
Square roots are used in various physics formulas. For instance, the formula for the period of a simple pendulum is \( T = 2\pi\sqrt{\frac{L}{g}} \), where \( T \) is the period, \( L \) is the length of the pendulum, and \( g \) is the acceleration due to gravity.
-
Engineering
In engineering, square roots are used to calculate structural responses and stresses. For example, the natural frequency of a structure like a bridge or building can be calculated using square roots, helping engineers predict how structures will react under different loads.
-
Finance
In finance, the volatility of a stock is often calculated using the square root of the variance of its returns. This helps investors understand the risk associated with different investments.
-
Statistics
Square roots are essential in statistics for calculating standard deviation, which is the square root of the variance. This measure indicates how spread out the values in a data set are around the mean.
The formula is: \( \sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2} \), where \( \sigma \) is the standard deviation, \( N \) is the number of data points, \( x_i \) are the individual data points, and \( \mu \) is the mean.
-
Computer Science
Square roots are used in computer science for various algorithms, including those in cryptography, graphics, and data analysis. For instance, the distance between two points in a 2D or 3D space is calculated using the Pythagorean theorem.
The formula in 2D is: \( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)
The formula in 3D is: \( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}
-
Navigation
In navigation, square roots are used to calculate distances between coordinates on maps. For example, to find the straight-line distance between two points, the Pythagorean theorem is applied.
-
Accident Investigations
Police use square roots to determine the speed of a car from the length of skid marks during accident investigations. The speed \( v \) can be found using the formula \( v = \sqrt{24d} \), where \( d \) is the length of the skid marks in feet.

Square Roots in Mathematics
Square roots play a crucial role in various branches of mathematics. Understanding square roots is essential for solving equations, working with geometric shapes, and performing calculations in different areas of math.
Definition and Basic Properties
The square root of a number \( n \) is a value \( x \) such that \( x^2 = n \). The square root is denoted by the radical symbol \( \sqrt{} \). For example, \( \sqrt{9} = 3 \) because \( 3^2 = 9 \).
- Positive and Negative Roots: Every positive number \( n \) has two square roots: \( \sqrt{n} \) (positive) and \( -\sqrt{n} \) (negative).
- Perfect Squares: A number is a perfect square if its square root is an integer. For instance, 16 is a perfect square because \( \sqrt{16} = 4 \).
- Non-Perfect Squares: Non-perfect squares have irrational square roots. For example, \( \sqrt{2} \) is approximately 1.414, and it cannot be expressed as a simple fraction.
Geometric Interpretation
In geometry, the square root function is often used to determine the length of sides in right-angled triangles using the Pythagorean theorem:
\[
c = \sqrt{a^2 + b^2}
\]
where \( c \) is the hypotenuse and \( a \) and \( b \) are the other two sides. For example, if \( a = 3 \) and \( b = 4 \), then \( c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \).
Solving Equations
Square roots are frequently used to solve quadratic equations. For instance, to solve \( x^2 = 49 \), we take the square root of both sides to get \( x = \pm\sqrt{49} = \pm7 \).
Square Root Functions and Graphs
The square root function \( f(x) = \sqrt{x} \) is a fundamental function in mathematics. It is defined for all non-negative \( x \) and its graph is a curve that starts at the origin (0,0) and increases slowly as \( x \) increases.
The domain of the square root function is \( x \geq 0 \), and the range is also \( y \geq 0 \). The function is continuous and increases monotonically.
Advanced Applications
Square roots are utilized in various advanced mathematical concepts and calculations:
- Calculus: In calculus, square roots appear in derivative and integral calculations, especially when dealing with functions involving squares and square roots.
- Algebra: Simplifying expressions and solving polynomial equations often involve square roots. For example, the quadratic formula involves square roots: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
- Trigonometry: In trigonometry, square roots are used in the Pythagorean identities and in determining the lengths of sides in various trigonometric problems.
Conclusion
Square roots are an integral part of mathematics, providing essential tools for solving equations, analyzing geometric figures, and performing complex calculations. Mastery of square roots is fundamental for advancing in various fields of math and science.
Square Roots in Physics
Square roots play a significant role in various aspects of physics, providing solutions to a wide range of problems. Here are some notable applications:
-
Wave Speed on a Stretched String
The speed \( v \) of a wave on a string under tension can be calculated using the formula:
\[
v = \sqrt{\frac{F_T}{\mu}}
\]where \( F_T \) is the tension in the string and \( \mu \) is the linear mass density of the string.
-
Uncertainty in Counting Phenomena
In scenarios involving inherently random phenomena, such as radioactive decay, the uncertainty \( \sigma \) in the measurement is equal to the square root of the number of measurements \( N \). This relationship is given by:
\[
\sigma = \sqrt{N}
\] -
Kinetic Energy and Potential Energy
In problems involving potential and kinetic energy, the equation \( v = \sqrt{2gh} \) is frequently encountered, where:
\[
v = \sqrt{2gh}
\]Here, \( g \) is the acceleration due to gravity, and \( h \) is the height from which an object falls. This equation is used to determine the velocity of an object in free fall.
These examples illustrate the fundamental role of square roots in solving complex physical problems, making them a crucial mathematical tool in the field of physics.
Square Roots in Engineering
Square roots play a crucial role in various fields of engineering. They are fundamental in calculations and design processes, providing essential insights and solutions for complex problems. Here are some notable applications of square roots in engineering:
- Signal Processing: Square roots are used in calculating the root mean square (RMS) value of signals. The RMS value is crucial for analyzing the power and magnitude of alternating current (AC) signals and other waveforms.
- Structural Engineering: In structural engineering, square roots are used in calculating stress, strain, and load-bearing capacities of materials. For example, the buckling load of a column can be determined using square root calculations.
- Electrical Engineering: Electrical engineers use square roots in power calculations. The RMS value of voltage or current is determined using the square root of the mean of the squares of the instantaneous values.
- Mechanical Engineering: In dynamics and vibrations, the natural frequency of a system is often determined using the square root of stiffness over mass. This is essential in designing systems that avoid resonant frequencies.
- Fluid Dynamics: Engineers use square roots to calculate flow rates and velocities in various fluid systems. For example, the speed of sound in a fluid can be determined using the square root of the ratio of the bulk modulus to the density of the fluid.
Here is a detailed example in electrical engineering:
Calculating RMS Value of an AC Signal
The RMS value of an AC signal is given by the formula:
\[
\text{RMS} = \sqrt{\frac{1}{T} \int_0^T [f(t)]^2 \, dt}
\]
For a sine wave, this simplifies to:
\[
\text{RMS} = \frac{A}{\sqrt{2}}
\]
where \(A\) is the amplitude of the sine wave. This calculation is critical in determining the effective power of AC signals in electrical circuits.
Another example is in the calculation of the buckling load of a column in structural engineering:
Buckling Load of a Column
The critical buckling load \(P_{cr}\) for a column can be calculated using Euler's formula:
\[
P_{cr} = \frac{\pi^2 E I}{(KL)^2}
\]
where \(E\) is the modulus of elasticity, \(I\) is the moment of inertia, \(K\) is the column effective length factor, and \(L\) is the unsupported length of the column. The square root function is used when deriving the critical load and understanding the stability of the structure.
These examples illustrate how square roots are indispensable in engineering, providing essential tools for analysis and design in various applications.
Square Roots in Computer Science
Square roots play a significant role in various computer science applications, ranging from algorithm design to performance evaluation. This section explores some key areas where square roots are essential.
1. Algorithm Design
In computer science, square roots are often used in algorithm design, particularly in algorithms involving geometric computations, optimization, and numerical methods. For example, finding the Euclidean distance between two points in a plane involves calculating the square root of the sum of the squares of the differences in their coordinates:
2. Computational Complexity
Many algorithms utilize the square root function to improve efficiency. For instance, the Square Root Decomposition technique is used in data structures to answer range queries efficiently. This method involves dividing an array into blocks of size √n, which helps in reducing the time complexity of certain operations.
def query(l, r):
sum = 0
while l <= r and l % sqrt_n != 0:
sum += arr[l]
l += 1
while l + sqrt_n <= r:
sum += block_sum[l // sqrt_n]
l += sqrt_n
while l <= r:
sum += arr[l]
l += 1
return sum
3. Performance Metrics
The Root Mean Square Error (RMSE) is a commonly used metric in regression models to measure the average magnitude of the errors. It is calculated as the square root of the average of the squared differences between predicted and actual values:
Here, represents the actual values, represents the predicted values, and is the number of observations.
4. Numerical Methods
One of the most popular methods for finding square roots in computer science is Newton's Method (also known as the Newton-Raphson method). This iterative method starts with an initial guess and repeatedly applies the formula:
Here, is the current approximation, and is the number whose square root is being computed. The process is repeated until the difference between successive approximations is smaller than a predetermined threshold.
5. Machine Learning and Data Science
In machine learning and data science, square roots are used in various ways, including feature scaling, normalization, and evaluation metrics. For example, RMSE is a crucial metric for assessing the accuracy of predictive models, helping data scientists understand model performance and make necessary adjustments.
Understanding the importance and applications of square roots in computer science helps in designing efficient algorithms, evaluating model performance, and solving complex computational problems.

Square Roots of Negative Numbers
In mathematics, the square root of a negative number does not yield a real number, since the square of any real number is non-negative. Instead, we introduce the concept of imaginary numbers to handle the square roots of negative numbers.
The imaginary unit, denoted by \( i \), is defined as:
\[
i = \sqrt{-1}
\]
This definition allows us to express the square root of any negative number.
To find the square root of a negative number \( -n \), follow these steps:
- Rewrite the negative number in terms of \( i \): \[ \sqrt{-n} = \sqrt{n} \cdot \sqrt{-1} = \sqrt{n} \cdot i \]
- For example, consider \( \sqrt{-9} \):
- First, find the square root of the positive counterpart: \( \sqrt{9} = 3 \).
- Then, multiply by \( i \): \( \sqrt{-9} = 3i \).
Here are some additional examples:
| Negative Number | Square Root |
|---|---|
| \( -4 \) | \( 2i \) |
| \( -16 \) | \( 4i \) |
| \( -25 \) | \( 5i \) |
For complex numbers, the concept extends naturally. If you have a complex number \( -a + bi \), where \( a \) and \( b \) are real numbers and \( a > 0 \), the square root can be found by:
- First, find the magnitude \( r \): \[ r = \sqrt{a^2 + b^2} \]
- Calculate the argument \( \theta \): \[ \theta = \tan^{-1}\left(\frac{b}{-a}\right) \]
- Then, use the square root formula in polar form: \[ \sqrt{-a + bi} = \sqrt{r} \left( \cos \frac{\theta}{2} + i \sin \frac{\theta}{2} \right) \]
Thus, the introduction of the imaginary unit \( i \) allows us to handle square roots of negative numbers by extending our number system to include complex numbers. This provides a comprehensive way to express and manipulate square roots of negative values in various mathematical contexts.
Imaginary Numbers and Their Properties
Imaginary numbers are a fundamental extension of the real number system, introduced to provide solutions to equations that do not have real roots. The basic imaginary unit, denoted as \( i \), is defined by the property:
\[
i^2 = -1
\]
This means that \( i \) is the square root of \(-1\).
Imaginary numbers are often written in the form \( bi \), where \( b \) is a real number. When combined with real numbers, they form complex numbers, written as \( a + bi \) where \( a \) and \( b \) are real numbers.
Here are some key properties and operations involving imaginary numbers:
- Addition and Subtraction:
Imaginary numbers add and subtract like real numbers, but the imaginary unit \( i \) is treated separately. For instance:
\[
(3 + 4i) + (1 - 2i) = 4 + 2i
\]
\[
(3 + 4i) - (1 - 2i) = 2 + 6i - Multiplication:
When multiplying imaginary numbers, use the distributive property and the fact that \( i^2 = -1 \):
\[
(2 + 3i)(1 + 4i) = 2 + 8i + 3i + 12i^2 = 2 + 11i - 12 = -10 + 11i
\]
\p>Note that the term \( 12i^2 \) becomes \(-12\) because \( i^2 = -1 \). - Division:
To divide by a complex number, multiply the numerator and the denominator by the conjugate of the denominator:
\[
\frac{3 + 2i}{1 - 4i} = \frac{(3 + 2i)(1 + 4i)}{(1 - 4i)(1 + 4i)} = \frac{3 + 12i + 2i + 8i^2}{1 - 16i^2} = \frac{3 + 14i - 8}{1 + 16} = \frac{-5 + 14i}{17} = -\frac{5}{17} + \frac{14}{17}i - Conjugate:
The conjugate of an imaginary number \( a + bi \) is \( a - bi \). Conjugates are useful for rationalizing denominators and finding the modulus of complex numbers. For example, the conjugate of \( 3 + 4i \) is \( 3 - 4i \).
- Modulus:
The modulus (or absolute value) of an imaginary number \( a + bi \) is given by:
\[
|a + bi| = \sqrt{a^2 + b^2}
\]
For example, the modulus of \( 3 + 4i \) is:
\[
|3 + 4i| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5 - Polar Form:
Imaginary numbers can also be expressed in polar form as \( r(\cos \theta + i \sin \theta) \), where \( r = |a + bi| \) is the modulus and \( \theta = \tan^{-1}\left(\frac{b}{a}\right) \) is the argument. This form is useful for multiplication, division, and finding powers:
\[
3 + 4i = 5(\cos 0.93 + i \sin 0.93)
In summary, imaginary numbers extend the real number system and provide a way to solve equations involving the square root of negative numbers. They exhibit unique properties and can be manipulated using algebraic rules similar to real numbers, while also being expressible in polar form for more advanced operations.
Advanced Topics in Square Roots
Square roots play a significant role in various advanced mathematical concepts and applications. This section explores deeper topics associated with square roots, including their properties, behaviors, and applications in different fields.
Below are some advanced topics in square roots:
- Square Root Algorithms:
Several algorithms exist for computing square roots, including:
- Newton's Method: An iterative approach based on the function \( f(x) = x^2 - n \): \[ x_{k+1} = \frac{1}{2} \left( x_k + \frac{n}{x_k} \right) \] Start with an initial guess \( x_0 \) and iterate until the desired accuracy is reached.
- Binary Search Method: Uses binary search to find the square root by narrowing the interval \([0, n]\) where the square root lies.
- Babylonian Method: Also known as Heron's method, an ancient technique similar to Newton's method: \[ x_{k+1} = \frac{1}{2} \left( x_k + \frac{n}{x_k} \right) \]
- Generalizations of Square Roots:
Square roots can be generalized in various ways:
- n-th Roots: The n-th root of a number \( a \) is a value \( b \) such that \( b^n = a \). For example, the cube root of \( 8 \) is \( 2 \), because \( 2^3 = 8 \).
- Matrix Square Roots: For a matrix \( A \), a matrix \( B \) is a square root of \( A \) if \( B^2 = A \). Matrix square roots have applications in solving differential equations and other areas of linear algebra.
- Operator Square Roots: In functional analysis, square roots of operators extend the concept of square roots to infinite-dimensional spaces.
- Square Roots in Different Number Systems:
The behavior of square roots varies across different number systems:
- Rational Numbers: Square roots of rational numbers are not always rational. For example, \( \sqrt{2} \) is irrational.
- Complex Numbers: Every non-zero complex number has two square roots, involving imaginary components.
- Quaternions: In quaternion algebra, square roots extend to four-dimensional numbers with real and imaginary parts.
- Applications of Square Roots:
Square roots have numerous applications in advanced fields:
- Physics: Used in solving equations related to wave functions, quantum mechanics, and relativity.
- Engineering: Applied in control theory, signal processing, and structural analysis.
- Statistics: Used in standard deviation calculations and other statistical measures.
- Cryptography: Involves square roots in the context of modular arithmetic and public key algorithms.
These advanced topics illustrate the diverse applications and deeper understanding of square roots in various mathematical and applied contexts, highlighting their importance beyond basic arithmetic operations.
Square Root Functions and Graphs
Square root functions are a fundamental type of mathematical function characterized by the square root operation. They are commonly written in the form:
\[
f(x) = \sqrt{x}
\]
These functions are defined for non-negative values of \( x \) (i.e., \( x \geq 0 \)) and have unique properties and graphs.
Here’s an in-depth look at square root functions and their graphs:
- Definition and Basic Properties:
The square root function \( f(x) = \sqrt{x} \) has the following properties:
- Domain: The domain is \( x \geq 0 \), since the square root of a negative number is not defined in the real number system.
- Range: The range is \( f(x) \geq 0 \), since square roots are non-negative.
- Intercept: The function passes through the origin, \((0, 0)\).
- Increasing Nature: The function is increasing for \( x \geq 0 \), meaning as \( x \) increases, \( f(x) \) also increases.
- Continuity: The square root function is continuous for all \( x \geq 0 \).
- Graph of the Square Root Function:
The graph of \( f(x) = \sqrt{x} \) is a curve that starts at the origin and rises gradually. Here’s a step-by-step guide to sketching the graph:
- Plot the point at the origin \((0, 0)\).
- Choose a few positive \( x \)-values and calculate \( f(x) \):
\( x \) \( f(x) = \sqrt{x} \) 0 0 1 1 4 2 9 3 16 4 - Plot these points on the coordinate plane.
- Draw a smooth curve through the points, starting at the origin and moving to the right.
The graph resembles the right half of a sideways parabola.
- Transformations of the Square Root Function:
Square root functions can be transformed using various techniques:
- Vertical Shifts: The function \( f(x) = \sqrt{x} + c \) shifts the graph up by \( c \) units if \( c > 0 \), and down by \( c \) units if \( c < 0 \).
- Horizontal Shifts: The function \( f(x) = \sqrt{x - h} \) shifts the graph to the right by \( h \) units if \( h > 0 \), and to the left by \( h \) units if \( h < 0 \).
- Vertical Stretching/Compressing: The function \( f(x) = a \sqrt{x} \) stretches the graph vertically by a factor of \( a \) if \( a > 1 \), and compresses it if \( 0 < a < 1 \).
- Reflections: The function \( f(x) = -\sqrt{x} \) reflects the graph across the x-axis, while \( f(x) = \sqrt{-x} \) reflects it across the y-axis.
Here is an example of a transformation:
For \( f(x) = 2 \sqrt{x - 3} + 1 \):
- The graph is shifted 3 units to the right.
- It is vertically stretched by a factor of 2.
- It is shifted 1 unit up.
- Applications of Square Root Functions:
Square root functions are used in various applications, such as:
- Physics: Modeling phenomena such as wave functions and decay processes.
- Engineering: Analyzing stress and strain in materials.
- Economics: Modeling diminishing returns and risk assessments.
- Biology: Describing growth rates and diffusion processes.
Understanding square root functions and their graphical representations is essential for solving problems in various scientific and engineering disciplines. By manipulating these functions, one can model and analyze a wide range of real-world scenarios.
Solving Equations Involving Square Roots
Equations involving square roots can be solved using various techniques depending on their complexity. This section provides a step-by-step guide to solving such equations.
- Isolate the Square Root Term:
The first step in solving an equation with a square root is to isolate the square root term on one side of the equation. For example, consider the equation:
\[
\sqrt{x} + 3 = 7
\]
To isolate the square root, subtract 3 from both sides:
\[
\sqrt{x} = 4 - Square Both Sides:
Once the square root is isolated, eliminate it by squaring both sides of the equation. Using the previous example:
\[
(\sqrt{x})^2 = 4^2
\]
This simplifies to:
\[
x = 16 - Check for Extraneous Solutions:
It’s essential to check for extraneous solutions by substituting the result back into the original equation. For the example:
\[
\sqrt{16} + 3 = 7 \implies 4 + 3 = 7
\]
The solution \( x = 16 \) is valid. - Solving More Complex Equations:
For equations involving multiple square roots or additional terms, follow these steps:
- Example 1: Solve
\[
\sqrt{x + 1} - \sqrt{x - 1} = 1
- Isolate one of the square roots: \[ \sqrt{x + 1} = \sqrt{x - 1} + 1
- Square both sides: \[ (\sqrt{x + 1})^2 = (\sqrt{x - 1} + 1)^2 \] Simplifying gives: \[ x + 1 = x - 1 + 2\sqrt{x - 1} + 1 \] Which simplifies to: \[ x + 1 = x + 2\sqrt{x - 1} \]
- Isolate the remaining square root: \[ 1 = 2\sqrt{x - 1} \] Divide both sides by 2: \[ \frac{1}{2} = \sqrt{x - 1} \] Square both sides again: \[ \left(\frac{1}{2}\right)^2 = (\sqrt{x - 1})^2 \] Simplifies to: \[ \frac{1}{4} = x - 1 \] Adding 1 to both sides: \[ x = \frac{5}{4} \]
- Check the solution: \[ \sqrt{\frac{5}{4} + 1} - \sqrt{\frac{5}{4} - 1} = 1 \] Simplifying gives: \[ \sqrt{\frac{9}{4}} - \sqrt{\frac{1}{4}} = 1 \implies \frac{3}{2} - \frac{1}{2} = 1 \] The solution \( x = \frac{5}{4} \) is valid.
- Example 2: Solve
\[
\sqrt{x + 2} = x - 2
- Square both sides: \[ (\sqrt{x + 2})^2 = (x - 2)^2 \] Simplifies to: \[ x + 2 = x^2 - 4x + 4 \]
- Rearrange into a quadratic equation: \[ 0 = x^2 - 5x + 2 \]
- Solve the quadratic equation using the quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \): \[ x = \frac{5 \pm \sqrt{25 - 8}}{2} = \frac{5 \pm \sqrt{17}}{2} \] This yields two solutions: \[ x = \frac{5 + \sqrt{17}}{2} \quad \text{and} \quad x = \frac{5 - \sqrt{17}}{2} \]
- Check both solutions: \p>For \( x = \frac{5 + \sqrt{17}}{2} \): \[ \sqrt{\frac{5 + \sqrt{17}}{2} + 2} = \frac{5 + \sqrt{17}}{2} - 2 \] For \( x = \frac{5 - \sqrt{17}}{2} \): \[ \sqrt{\frac{5 - \sqrt{17}}{2} + 2} = \frac{5 - \sqrt{17}}{2} - 2 \] Simplification confirms which solutions are valid.
- Example 1: Solve
\[
\sqrt{x + 1} - \sqrt{x - 1} = 1
- Common Pitfalls:
Be aware of common mistakes, such as:
- Not isolating the square root term completely before squaring.
- Forgetting to check for extraneous solutions.
- Misapplying algebraic principles when manipulating terms.
Solving equations involving square roots requires careful isolation of the square root terms, proper squaring techniques, and thorough checking of solutions to ensure their validity. These steps will help in solving both simple and complex square root equations effectively.
Square Root Transformations
Square root transformations involve modifying the basic square root function to create new functions with different properties. These transformations include translations, reflections, stretches, and compressions. This section covers various types of transformations applied to the square root function.
- Vertical Shifts:
A vertical shift moves the graph of the square root function up or down. The general form is:
\[
f(x) = \sqrt{x} + c
\]
where \( c \) is a constant.- If \( c > 0 \), the graph shifts up by \( c \) units.
- If \( c < 0 \), the graph shifts down by \( c \) units.
Example: For \( f(x) = \sqrt{x} + 2 \), the graph of \( \sqrt{x} \) is shifted up by 2 units.
- Horizontal Shifts:
A horizontal shift moves the graph left or right. The general form is:
\[
f(x) = \sqrt{x - h}
\]
where \( h \) is a constant.- If \( h > 0 \), the graph shifts right by \( h \) units.
- If \( h < 0 \), the graph shifts left by \( h \) units.
Example: For \( f(x) = \sqrt{x - 3} \), the graph of \( \sqrt{x} \) shifts to the right by 3 units.
- Vertical Stretches and Compressions:
Vertical stretching or compressing alters the steepness of the graph. The general form is:
\[
f(x) = a \sqrt{x}
\]
where \( a \) is a constant.- If \( |a| > 1 \), the graph stretches vertically by a factor of \( |a| \).
- If \( 0 < |a| < 1 \), the graph compresses vertically by a factor of \( |a| \).
Example: For \( f(x) = 2 \sqrt{x} \), the graph is vertically stretched by a factor of 2.
- Horizontal Stretches and Compressions:
Horizontal stretching or compressing changes the width of the graph. The general form is:
\[
f(x) = \sqrt{k x}
\]
where \( k \) is a constant.- If \( |k| > 1 \), the graph compresses horizontally by a factor of \( |k| \).
- If \( 0 < |k| < 1 \), the graph stretches horizontally by a factor of \( |k| \).
Example: For \( f(x) = \sqrt{0.5x} \), the graph is horizontally stretched by a factor of 2.
- Reflections:
Reflections flip the graph across an axis. There are two types of reflections:
- Reflection across the x-axis:
The function is:
\[
f(x) = -\sqrt{x}
\]
This flips the graph upside down.Example: For \( f(x) = -\sqrt{x} \), the graph of \( \sqrt{x} \) is reflected across the x-axis.
- Reflection across the y-axis:
The function is:
\[
f(x) = \sqrt{-x}
\]
This flips the graph left to right.Example: For \( f(x) = \sqrt{-x} \), the graph of \( \sqrt{x} \) is reflected across the y-axis.
- Reflection across the x-axis:
- Combining Transformations:
Multiple transformations can be applied to a square root function to create complex graphs. These transformations can be applied in a sequence:
- Example: For
\[
f(x) = -2 \sqrt{x - 3} + 4
\]
This function combines several transformations:
- Horizontal shift: \( x \) is replaced with \( x - 3 \), shifting the graph 3 units to the right.
- Vertical stretch: The factor of 2 vertically stretches the graph by a factor of 2.
- Reflection: The negative sign reflects the graph across the x-axis.
- Vertical shift: Adding 4 shifts the graph up by 4 units.
Plot the transformations step-by-step to understand the effect on the graph.
- Example: For
\[
f(x) = -2 \sqrt{x - 3} + 4
\]
By understanding and applying these transformations, you can manipulate the square root function to fit various scenarios in mathematical modeling, data analysis, and graphical interpretations.
Khám phá lý thuyết chứng minh căn bậc hai của bất kỳ số nguyên nào là vô tỉ, ngoại trừ các số chính phương.
Bằng chứng rằng căn bậc hai của BẤT KỲ số nguyên nào là vô tỉ (ngoại trừ số chính phương)
READ MORE:
Phương pháp Newton: Căn bậc hai nhanh nhất thế giới
Phương pháp Newton: Căn bậc hai nhanh nhất thế giới