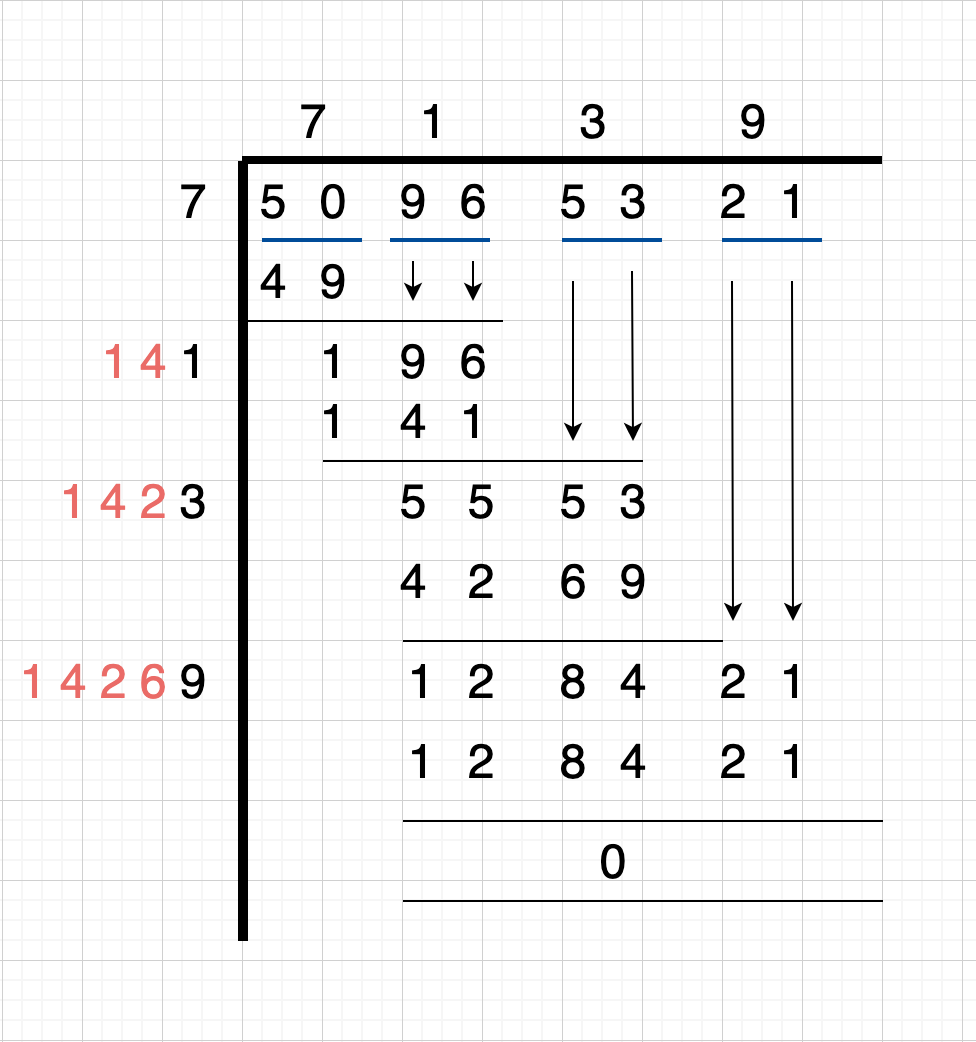
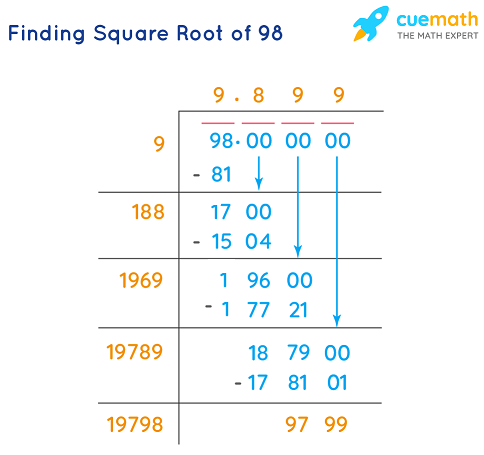
Topic square root how to calculate: Understanding how to calculate the square root is essential for mastering various mathematical concepts. This article breaks down the methods to find square roots, including prime factorization and long division, making it easy for anyone to grasp. Learn the best techniques to simplify your calculations and apply these skills confidently in your studies and everyday life.
Table of Content
- Understanding Square Roots
- Introduction
- Perfect Squares
- Square Roots of Decimals
- Square Roots of Negative Numbers and Complex Numbers
- Simplifying Square Roots
- Using Square Root Calculators
- Applications of Square Roots
- Example Calculations
- Conclusion
- YOUTUBE: Hướng dẫn cách tính căn bậc hai và tìm hiểu về các chữ số đã thay đổi toán học mãi mãi.
Understanding Square Roots
The square root of a number is a value which, when multiplied by itself, gives the original number. The square root is the inverse operation of squaring a number. It is commonly represented by the radical symbol (√).
Definition and Symbol
Suppose x is the square root of y, then it is represented as x = √y, or x² = y. Here, '√' is the radical symbol used to denote the root of numbers. The square of a positive number gives the original number when the square root is applied.
Examples of Square Roots
- The square root of 9 is 3, because 3 × 3 = 9, so √9 = 3.
- The square root of 25 is 5, because 5 × 5 = 25, so √25 = 5.
- The square root of 16 is 4, because 4 × 4 = 16, so √16 = 4.
Methods to Calculate Square Roots
Prime Factorization Method
This method is used for perfect squares. For example:
- Find the square root of 81.
Prime factorization: 81 = 3 × 3 × 3 × 3, so √81 = 3 × 3 = 9.
- Find the square root of 625.
Prime factorization: 625 = 5 × 5 × 5 × 5, so √625 = 5 × 5 = 25.
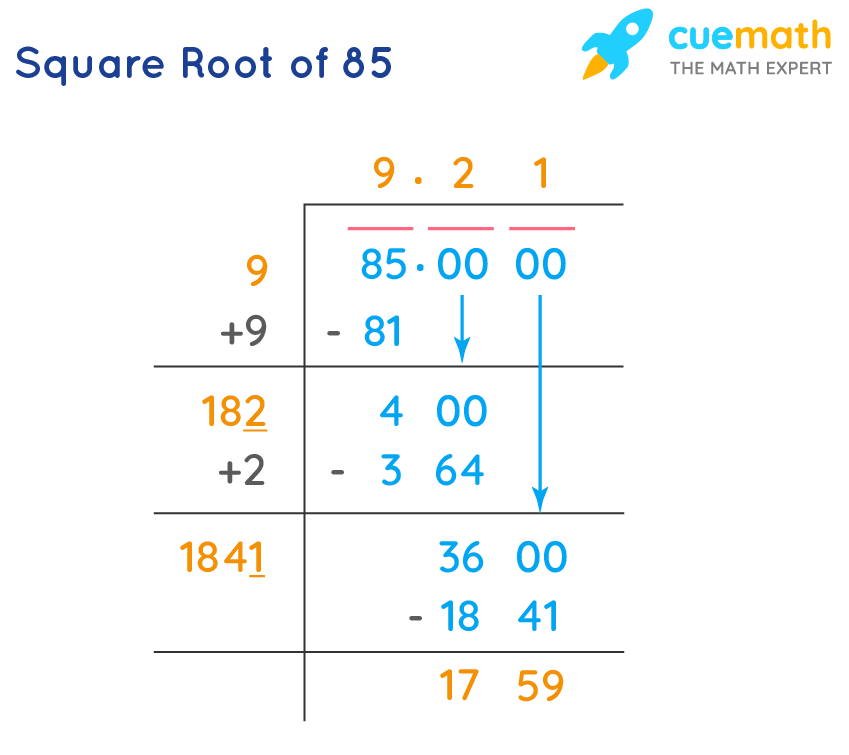
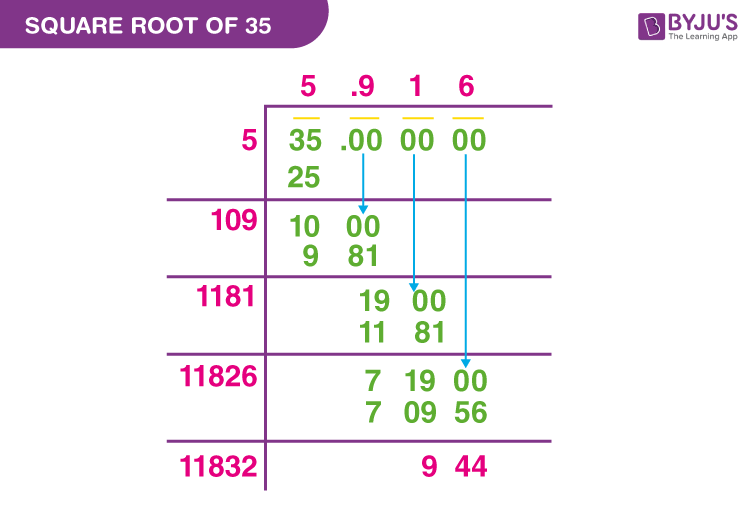
Long Division Method
This method can be used for both perfect and non-perfect squares. Here's an example for a non-perfect square:
- Write the number (e.g., 5) as 5.00000000.
- Find the largest number whose square is less than or equal to the number in the leftmost group.
- Use this number as the divisor and the quotient.
- Repeat the process to get more decimal places.
- Example: Finding √2 using long division yields approximately 1.4142.
Square Root of Decimal Numbers
To find the square root of a decimal number, we can convert it into a fraction and then simplify. For example:
- √6.25 can be written as √(625/100) = √625 / √100 = 25 / 10 = 2.5.
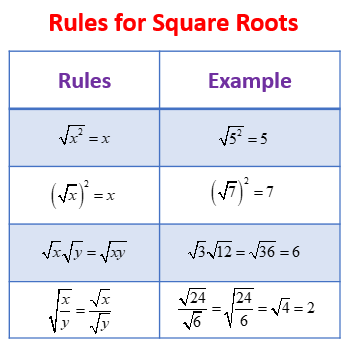
Properties of Square Roots
- If a number is a perfect square, it has an integer square root.
- A number with an even number of zeros at the end will have a square root.
- Two square roots can be multiplied: √a × √b = √(a × b).
- When the same square roots are multiplied, the result is the radicand: √a × √a = a.
Complex and Negative Numbers
The square root of a negative number is a complex number. For example, the square root of -9 is represented as 3i, where i is the imaginary unit.
Common Square Root Values
| Number | Square Root |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
Understanding how to calculate and use square roots is fundamental in various mathematical applications, from solving quadratic equations to understanding geometric properties.

READ MORE:
Introduction
The square root of a number is a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the original number. The process of calculating square roots can be approached through several methods, including prime factorization, long division, and estimation techniques. This article will guide you through these methods step-by-step, making the calculation of square roots straightforward and accessible for both perfect and imperfect squares.
Perfect Squares
A perfect square is an integer that is the square of another integer. Here are some key points about perfect squares:
- They have whole number square roots.
- The square root of a perfect square is exact and not a decimal.
- Examples of perfect squares include 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, and so on.
- Perfect squares follow the pattern of \( n^2 \), where \( n \) is an integer.
Square Roots of Decimals
Calculating square roots of decimal numbers involves similar methods as whole numbers but requires careful handling of the decimal places. Here’s how you can approach it:
- Estimate the Integer Part: Ignore the decimal point temporarily and find the square root of the integer part of the number.
- Adjust for Decimal Places: Determine the decimal places by considering the square root of the decimal part of the number. This often involves trial and error or estimation techniques.
- Use Iterative Methods: Iteratively refine your estimate, adjusting the decimal places until you reach the desired accuracy.
For example, to find \( \sqrt{5.76} \):
| Step | Process |
| 1. | Estimate \( \sqrt{5} \approx 2.236 \) |
| 2. | Consider \( \sqrt{0.76} \):
|
With practice, calculating square roots of decimals becomes more intuitive, combining estimation with mathematical precision.
Square Roots of Negative Numbers and Complex Numbers
Calculating square roots of negative numbers and complex numbers involves understanding the concept of imaginary numbers and the imaginary unit \( i \), where \( i^2 = -1 \). Here’s how you can approach it:
- Understand Imaginary Numbers: Recognize that square roots of negative numbers result in complex numbers.
- Use the Formula: For a complex number \( z = a + bi \), the square roots are given by: \[ \sqrt{z} = \pm \sqrt{\frac{|z| + a}{2}} + i \cdot \text{sgn}(b) \cdot \sqrt{\frac{|z| - a}{2}} \] where \( |z| = \sqrt{a^2 + b^2} \) and \( \text{sgn}(b) \) is the sign of \( b \).
- Example Calculation: For \( \sqrt{-9} \):
Step Process 1. Recognize \( -9 = 9i^2 \). 2. Apply the formula: \( \sqrt{-9} = \pm \sqrt{\frac{9 + 0}{2}} + i \cdot \text{sgn}(0) \cdot \sqrt{\frac{9 - 0}{2}} = \pm 3i \).
Mastering the calculation of square roots for negative and complex numbers enhances your understanding of mathematical concepts beyond real numbers.

Simplifying Square Roots
Simplifying square roots involves reducing the expression under the radical sign to its simplest form. Here’s how you can simplify square roots:
- Factorization Method: Factor the number inside the square root into its prime factors.
- Pairing Method: Look for pairs of identical factors inside the square root that can be taken out as a single factor.
- Rationalizing Denominators: Remove square roots from denominators by multiplying the numerator and denominator by the conjugate of the denominator.
For example, to simplify \( \sqrt{72} \):
| Step | Process |
| 1. | Factorize \( 72 = 2^3 \times 3^2 \). |
| 2. | Take out pairs: \( \sqrt{72} = \sqrt{2^3 \times 3^2} = 6\sqrt{2} \). |
Simplifying square roots makes calculations easier and expressions more manageable in mathematical operations.
Using Square Root Calculators
Square root calculators are tools that simplify the process of finding the square root of a number. These calculators can be found online or as part of scientific calculators. Here’s how to use them effectively:
-
Access a Square Root Calculator:
- Open an online square root calculator via a web browser or use the square root function on a scientific calculator.
-
Enter the Number:
- Type or input the number for which you need the square root.
-
Calculate:
- Press the square root button (√) on your calculator. If you are using an online calculator, click the 'Calculate' button.
-
View the Result:
- The square root of the entered number will be displayed immediately.
Using square root calculators is straightforward and ensures accuracy, especially with more complex numbers. Here’s an example of using an online square root calculator:
- Navigate to an online square root calculator page.
- Input the number 49 into the input field.
- Click the 'Calculate' button.
- The calculator will display the result: 7.
Many calculators also provide additional features, such as showing the step-by-step process of the calculation, handling complex numbers, and offering options to calculate the square roots of fractions or decimals.
| Type of Calculator | Features |
|---|---|
| Online Square Root Calculator | Accessible via web browsers, supports various input formats, offers additional functions like step-by-step solutions. |
| Scientific Calculator | Handheld device, supports a wide range of mathematical functions, including square roots, often used in educational settings. |
Using these calculators can significantly ease the process of solving mathematical problems involving square roots, making them a valuable tool for students, educators, and professionals alike.
Applications of Square Roots
The concept of square roots finds applications in various fields, ranging from mathematics and science to engineering and everyday problem-solving. Below are some detailed applications:
- Geometry and Trigonometry:
Square roots are essential in geometry for calculating the lengths of sides in right-angled triangles, using the Pythagorean theorem. For instance, if a right triangle has legs of lengths \(a\) and \(b\), the length of the hypotenuse \(c\) is given by \( c = \sqrt{a^2 + b^2} \).
- Algebra:
Square roots are used to solve quadratic equations. For example, in the equation \( ax^2 + bx + c = 0 \), the solutions for \( x \) can be found using the quadratic formula \( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \).
- Physics:
Square roots appear in various physics equations, such as calculating the RMS (Root Mean Square) velocity in kinetic theory of gases, or in the formula for the period \( T \) of a simple pendulum, \( T = 2\pi \sqrt{\frac{L}{g}} \), where \( L \) is the length of the pendulum and \( g \) is the acceleration due to gravity.
- Engineering:
In engineering, square roots are used in formulas for stress and strain, electrical engineering, signal processing, and many other areas. For example, the magnitude of a complex number \( z = a + bi \) is given by \( |z| = \sqrt{a^2 + b^2} \).
- Statistics:
The standard deviation, a measure of the dispersion or spread in a set of data, involves square roots. It is defined as \( \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2} \), where \( \mu \) is the mean of the data set, \( x_i \) are the individual data points, and \( N \) is the number of data points.
- Finance:
Square roots are used in finance to calculate volatility and to model the random behavior of stock prices using methods like the Black-Scholes model. The volatility \( \sigma \) of an asset's return is often estimated using the formula \( \sigma = \sqrt{\frac{1}{N-1} \sum_{i=1}^{N} (R_i - \bar{R})^2} \), where \( R_i \) are individual returns and \( \bar{R} \) is the average return.
These examples demonstrate the wide-ranging importance of square roots in various domains, making them a fundamental mathematical concept.
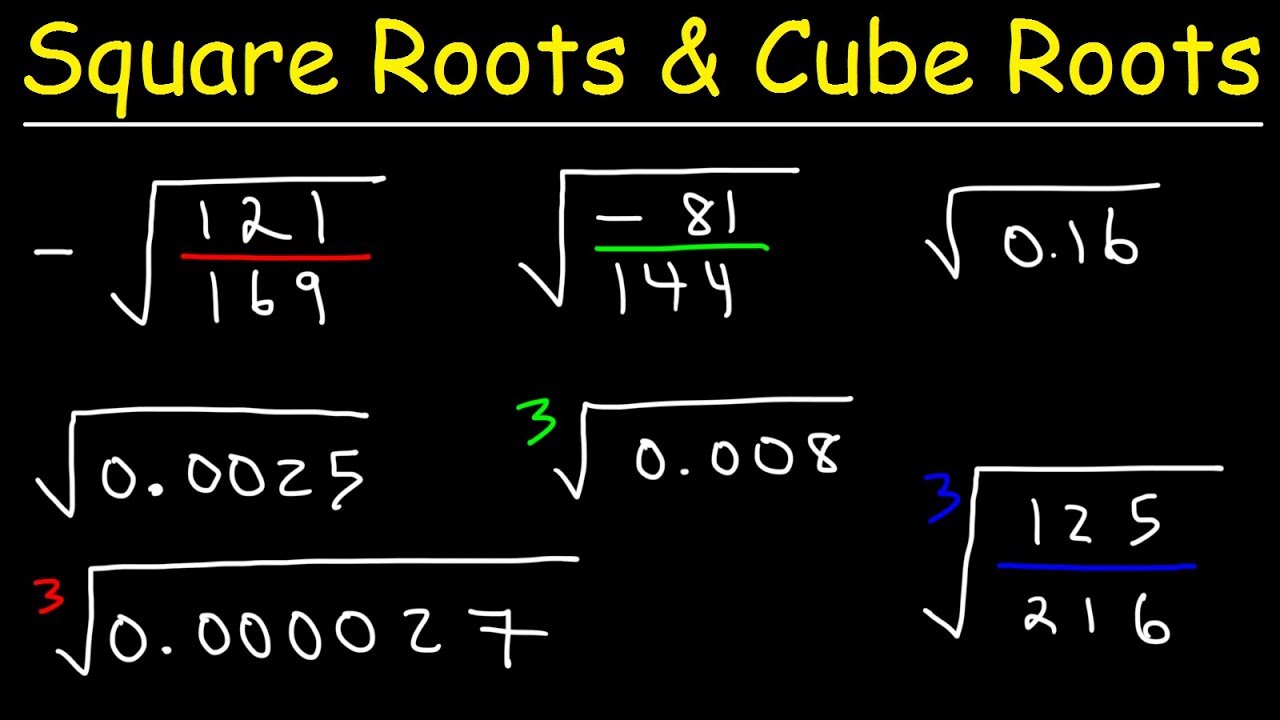
Example Calculations
Understanding how to calculate square roots is essential in mathematics. Here are detailed examples of both perfect square and non-perfect square calculations:
Perfect Square Examples
- Example 1: Calculate the square root of 64.
Since 64 is a perfect square, we can find its square root easily:
\[ \sqrt{64} = 8 \]
- Example 2: Calculate the square root of 144.
144 is another perfect square:
\[ \sqrt{144} = 12 \]
- Example 3: Calculate the square root of 225.
225 is a perfect square as well:
\[ \sqrt{225} = 15 \]
Non-Perfect Square Examples
- Example 1: Calculate the square root of 50.
50 is not a perfect square. We use estimation or a calculator to find:
\[ \sqrt{50} \approx 7.071 \]
- Example 2: Calculate the square root of 20.
Similarly, 20 is not a perfect square:
\[ \sqrt{20} \approx 4.472 \]
- Example 3: Calculate the square root of 10.
Again, for non-perfect squares like 10, we approximate:
\[ \sqrt{10} \approx 3.162 \]
For more complex calculations, it's useful to utilize a square root calculator or perform long division methods for precision.
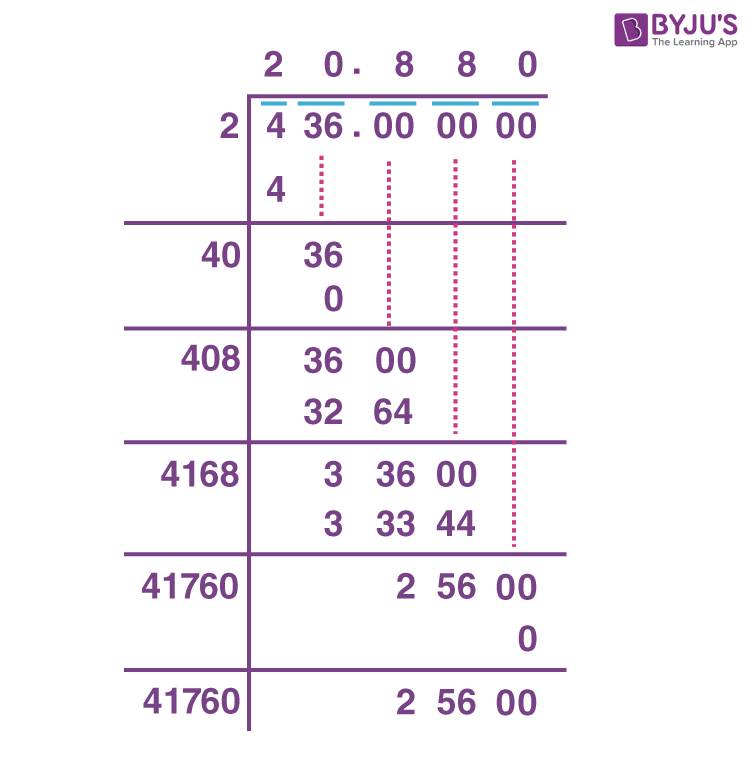
Conclusion
Understanding how to calculate square roots is a fundamental skill in mathematics that has various applications in different fields. By mastering the methods and properties of square roots, you can simplify complex problems and enhance your mathematical proficiency. Here are the key takeaways:
- Definition and Symbol: The square root of a number is a value that, when multiplied by itself, gives the original number. It is represented by the symbol \(\sqrt{}\).
- Methods of Calculation: There are several methods to calculate square roots, including the prime factorization method, long division method, and estimation method. Each method has its own advantages and is useful in different scenarios.
- Properties of Square Roots: Knowing properties such as the product property, quotient property, and power property helps in simplifying expressions and solving equations involving square roots.
- Common Square Root Values: Memorizing common square root values can save time and make calculations more efficient.
- Applications: Square roots are used in various real-world applications, from solving quadratic equations to calculating areas and in physics formulas.
- Square Roots of Special Numbers: Understanding how to handle square roots of decimals, negative numbers, and complex numbers expands your mathematical toolkit.
By practicing these methods and familiarizing yourself with the properties and common values of square roots, you will be well-equipped to tackle a wide range of mathematical problems. Whether you are a student, a professional, or simply someone with an interest in mathematics, the knowledge of square roots is invaluable and will serve you well in many aspects of problem-solving and analytical thinking.
Hướng dẫn cách tính căn bậc hai và tìm hiểu về các chữ số đã thay đổi toán học mãi mãi.
Cách Tính Căn Bậc Hai - Các Chữ Số Thay Đổi Toán Học Mãi Mãi
READ MORE:
Khám phá ý nghĩa của căn bậc hai và cách tính toán với thầy J trong video này. Video này sẽ giúp bạn hiểu rõ hơn về khái niệm và ứng dụng của căn bậc hai trong toán học.
Căn bậc hai là gì? | Toán học với thầy J