Topic square root of 5000: The square root of 5000 is an intriguing mathematical concept that combines simplicity with depth. Discover the methods to calculate, simplify, and understand its applications in various contexts. Whether for academic purposes or personal interest, this guide will enhance your knowledge and appreciation of this fundamental mathematical principle.
Table of Content
- Square Root of 5000
- Introduction to the Square Root of 5000
- Methods to Calculate the Square Root
- Properties of the Square Root of 5000
- Rationality of the Square Root of 5000
- Examples and Applications
- Simplifying the Square Root of 5000
- Square Root Calculation Techniques
- Calculating with Calculators and Software
- Frequently Asked Questions
- Tables and Charts
- YOUTUBE: Xét đoạn video '5000 cần phải chia cho số nhỏ nhất nào để nó trở thành một số mũ. #PhânTíchToánHọc'.
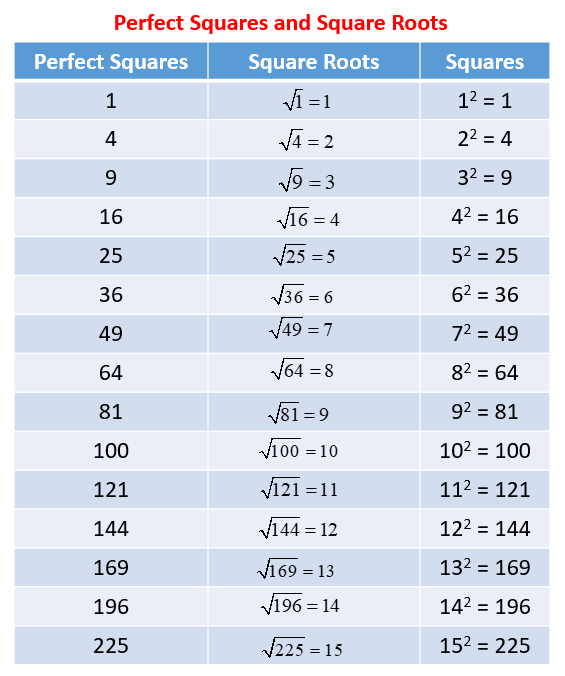
Square Root of 5000
The square root of 5000 is represented as and its approximate value is 70.71067811865476.
Mathematical Representation
The square root of 5000 can be written in various forms:
- Decimal: 70.71067811865476
- Radical form:
- Exponent form:
- Simplified radical form: 50
Properties
The square root of 5000 has the following properties:
- It is an irrational number because it cannot be expressed as a simple fraction.
- It is not a perfect square.
Calculation Methods
There are several methods to calculate the square root of 5000:
- Prime Factorization: Since 5000 is not a perfect square, this method is less effective.
- Long Division Method: This method is used for finding square roots of non-perfect squares and involves a process similar to long division.
- Calculator: Using a calculator is the simplest way to find the square root of 5000. Most calculators have a square root function.
Examples
Here are some examples involving the square root of 5000:
- Solving the equation : The solutions are , which is approximately .
- Finding the length of the side of a cube with a surface area of 30000 square inches: , which is approximately 70.7107 inches.
- Finding the radius of a circle with an area of 5000 square inches: , which is approximately 70.7107 inches.
Summary
| Value | Square Root |
|---|---|
| 5000 | ±70.71067811865476 |

READ MORE:
Introduction to the Square Root of 5000
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root of 5000, denoted as \( \sqrt{5000} \), represents a number which, when squared, results in 5000.
Understanding the square root of 5000 involves recognizing both its numerical and theoretical aspects. Below, we outline some key points:
- Definition: The square root of 5000 is a positive number \( x \) such that \( x^2 = 5000 \).
- Decimal Approximation: \( \sqrt{5000} \approx 70.71 \). This value is rounded to two decimal places and can be extended further for more precision.
- Simplified Form: The square root of 5000 can be simplified using prime factorization. Since 5000 = 2^3 \times 5^4, the square root can be simplified as \( \sqrt{5000} = 10 \sqrt{5} \).
- Properties:
- \( \sqrt{5000} \) is an irrational number, meaning it cannot be expressed as a simple fraction.
- It is a non-repeating, non-terminating decimal.
- Mathematical Representation: The square root of 5000 can be expressed using radical notation \( \sqrt{5000} \) or exponent notation \( 5000^{1/2} \).
In practical terms, the square root of 5000 can be used in various mathematical and real-world applications, including geometry, algebra, and numerical analysis. Whether simplifying expressions or solving equations, understanding how to work with the square root of 5000 can provide valuable insights into broader mathematical concepts.
Methods to Calculate the Square Root
Calculating the square root of 5000 can be done using various methods, each with its unique approach and level of precision. Here, we describe several common techniques:
- Manual Estimation Method:
- Identify two perfect squares between which 5000 lies. Since \( 70^2 = 4900 \) and \( 71^2 = 5041 \), the square root of 5000 lies between 70 and 71.
- Estimate a value between 70 and 71. Let's choose 70.5 as an initial estimate.
- Square the estimate: \( 70.5^2 = 4970.25 \).
- Since 4970.25 is less than 5000, adjust the estimate slightly upwards. Try 70.7: \( 70.7^2 = 4998.49 \).
- Continue adjusting the estimate until the squared value is close enough to 5000 for the desired precision.
- Prime Factorization Method:
- Prime factorize 5000: \( 5000 = 2^3 \times 5^4 \).
- Take the square root of each factor:
- \( \sqrt{2^3} = 2^{3/2} = 2 \sqrt{2} \)
- \( \sqrt{5^4} = 5^2 = 25 \)
- Combine the results: \[ \sqrt{5000} = \sqrt{2^3 \times 5^4} = 2 \sqrt{2} \times 25 = 50 \sqrt{2} \]
- Long Division Method:
- Pair the digits of 5000 from the decimal point: 50 and 00.
- Find the largest square less than or equal to 50: \( 7^2 = 49 \).
- Subtract and bring down the next pair of digits: \( 50 - 49 = 1 \). Bring down 00 to get 100.
- Double the divisor (7 becomes 14) and find the largest digit \( x \) such that \( 14x \times x \leq 100 \). Here, \( x = 0 \), so 0 is added to the quotient and 00 is brought down again.
- Continue this process until the desired precision is achieved.
- Using a Calculator:
- Enter 5000 into the calculator.
- Press the square root (\( \sqrt{} \)) function.
- The calculator displays \( \sqrt{5000} \approx 70.7107 \).
- Newton’s Method (Iterative Approach):
- Start with an initial guess \( x_0 \). Let \( x_0 = 70 \).
- Use the formula: \[ x_{n+1} = \frac{1}{2} \left( x_n + \frac{5000}{x_n} \right) \]
- Calculate the next approximation: \[ x_1 = \frac{1}{2} \left( 70 + \frac{5000}{70} \right) = 70.7143 \]
- Repeat the process until the approximation stabilizes.
These methods provide various ways to compute the square root of 5000, each suitable for different contexts and precision requirements. Understanding these methods enhances both computational skills and mathematical insight.
Properties of the Square Root of 5000
The square root of 5000, denoted as \( \sqrt{5000} \), possesses several interesting mathematical properties. These properties are important in various fields such as algebra, geometry, and number theory. Below, we detail some key characteristics:
- Value:
The numerical value of \( \sqrt{5000} \) is approximately 70.7107. This is a non-terminating, non-repeating decimal, indicating that \( \sqrt{5000} \) is an irrational number.
- Irrationality:
The square root of 5000 cannot be expressed as a fraction \( \frac{p}{q} \) where \( p \) and \( q \) are integers and \( q \neq 0 \). Its decimal representation goes on infinitely without repeating.
- Simplified Form:
Using prime factorization, 5000 can be expressed as \( 2^3 \times 5^4 \). Therefore, the square root can be simplified as:
\[
\sqrt{5000} = \sqrt{2^3 \times 5^4} = \sqrt{4 \times 1250} = 2 \times \sqrt{1250} = 2 \times 5 \sqrt{50} = 10 \sqrt{5}
\] - Algebraic Representation:
The square root of 5000 can be represented in radical form as \( \sqrt{5000} \), or in exponential form as \( 5000^{1/2} \).
- Geometric Interpretation:
In a geometric sense, \( \sqrt{5000} \) represents the length of the diagonal of a square whose area is 5000 square units. This can also be visualized as the distance from the origin to the point (5000, 0) in the Cartesian plane.
- Approximation and Use:
The square root of 5000 is often approximated for practical calculations. It is useful in solving quadratic equations, determining dimensions in geometry, and performing various scientific calculations.
- Square Property:
Squaring \( \sqrt{5000} \) returns the original number:
\[
(\sqrt{5000})^2 = 5000
\]
This property is fundamental in algebra and helps in verifying calculations involving square roots.
Understanding these properties of \( \sqrt{5000} \) helps in grasping broader mathematical concepts and applying them to solve complex problems.
Rationality of the Square Root of 5000
The concept of rationality in mathematics refers to whether a number can be expressed as a ratio of two integers. In the case of the square root of 5000, we examine its rationality by determining if it can be represented as a fraction \( \frac{p}{q} \), where \( p \) and \( q \) are integers with no common factors other than 1.
- Definition:
A rational number can be written as \( \frac{p}{q} \), where \( p \) and \( q \) are integers, and \( q \neq 0 \). An irrational number cannot be expressed in such a form.
- Prime Factorization:
To explore the rationality of \( \sqrt{5000} \), consider the prime factorization of 5000:
\[
5000 = 2^3 \times 5^4
\]
The square root is:
\[
\sqrt{5000} = \sqrt{2^3 \times 5^4} = 10 \sqrt{5}
\]
Since \( \sqrt{5} \) is irrational and cannot be simplified to a ratio of integers, \( \sqrt{5000} \) inherits this irrationality. - Proof by Contradiction:
Assume \( \sqrt{5000} \) is rational, so there exist integers \( a \) and \( b \) such that:
\[
\sqrt{5000} = \frac{a}{b}
\]
Squaring both sides gives:
\[
5000 = \frac{a^2}{b^2} \quad \text{or} \quad a^2 = 5000 b^2
\]
This implies that \( a^2 \) must be divisible by 5000. However, since 5000 is not a perfect square, \( a \) and \( b \) cannot satisfy this equation without leading to a contradiction. - Decimal Representation:
The decimal form of \( \sqrt{5000} \approx 70.71067811865475\ldots \) is non-terminating and non-repeating, which is characteristic of irrational numbers.
- Conclusion:
Since \( \sqrt{5000} \) cannot be represented as a fraction and its decimal expansion is non-repeating, it is classified as an irrational number. The square root of 5000 does not have an exact fractional representation.
Understanding the irrationality of \( \sqrt{5000} \) provides insights into the nature of numbers and helps in various mathematical contexts where exact rational representations are required.

Examples and Applications
The square root of 5000, \( \sqrt{5000} \), is used in a variety of mathematical and real-world applications. Below are some examples and practical uses:
- Geometry:
In geometry, the square root of 5000 can be used to calculate the length of the diagonal of a square with an area of 5000 square units. For a square with side length \( s \), the diagonal \( d \) can be found using:
\[
d = s \sqrt{2}
\]
If \( s = \sqrt{5000} \), then:
\[
d = \sqrt{5000} \times \sqrt{2} = \sqrt{10000} = 100
\] - Physics:
In physics, \( \sqrt{5000} \) can be used in formulas involving square roots, such as calculating the velocity needed to escape a gravitational field. If the escape velocity \( v \) is given by:
\[
v = \sqrt{\frac{2GM}{r}}
\]
where \( G \) is the gravitational constant, \( M \) is the mass of the planet, and \( r \) is the radius, then substituting appropriate values could involve using \( \sqrt{5000} \) as part of the calculations. - Engineering:
In engineering, the square root of 5000 might be used in structural analysis or design, particularly when dealing with load calculations or material stress. For example, if a beam's deflection \( \delta \) is proportional to \( \sqrt{W} \) where \( W \) is the load, and \( W = 5000 \) units, then:
\[
\delta \propto \sqrt{5000} \approx 70.71
\]
Understanding this value helps engineers design safer structures. - Statistics:
In statistics, the square root of 5000 can be used in standard deviation calculations. For a dataset where the variance \( \sigma^2 = 5000 \), the standard deviation \( \sigma \) is:
\[
\sigma = \sqrt{5000} \approx 70.71
\]
This measure indicates the dispersion of data points from the mean. - Finance:
In finance, \( \sqrt{5000} \) can appear in calculations involving compounded interest or risk assessment. For example, if a financial model estimates a return with variance 5000, the standard deviation \( \sigma \) of the return is:
\[
\sigma = \sqrt{5000} \approx 70.71
\]
This helps assess the volatility of investments. - Programming:
In programming, calculating \( \sqrt{5000} \) can be useful in algorithms involving distance metrics, optimization problems, or graphical computations. For example, in graphics, the Euclidean distance between points might involve calculations using \( \sqrt{5000} \).
These examples demonstrate the versatility and importance of \( \sqrt{5000} \) in various disciplines, highlighting its role in both theoretical and applied contexts.
Simplifying the Square Root of 5000
Simplifying the square root of 5000 involves expressing it in a more compact form using factors and properties of square roots. Here is a step-by-step guide to simplifying \( \sqrt{5000} \):
- Prime Factorization:
Begin by finding the prime factors of 5000. The factorization is:
\[
5000 = 2^3 \times 5^4
\] - Break Down the Radical:
Express the square root of 5000 in terms of its prime factors:
\[
\sqrt{5000} = \sqrt{2^3 \times 5^4}
\]
Separate the product inside the square root into individual square roots:
\[
\sqrt{5000} = \sqrt{2^3} \times \sqrt{5^4}
\] - Simplify Each Factor:
Next, simplify each square root individually:
\[
\sqrt{2^3} = \sqrt{8} = \sqrt{4 \times 2} = \sqrt{4} \times \sqrt{2} = 2 \sqrt{2}
\]
\[
\sqrt{5^4} = \sqrt{25 \times 25} = \sqrt{25} \times \sqrt{25} = 5 \times 5 = 25
\] - Combine Simplified Factors:
Multiply the simplified factors together:
\[
\sqrt{5000} = 2 \sqrt{2} \times 25 = 50 \sqrt{2}
\] - Verification:
To verify, we can square the simplified form and check if it equals 5000:
\[
(50 \sqrt{2})^2 = 50^2 \times (\sqrt{2})^2 = 2500 \times 2 = 5000
\]
This confirms that \( 50 \sqrt{2} \) is the correct simplified form of \( \sqrt{5000} \).
The simplified form of the square root of 5000 is \( 50 \sqrt{2} \). This expression is often more convenient for further calculations and provides a clearer understanding of the components of the original number.
Square Root Calculation Techniques
Calculating the square root of a number like 5000 can be approached through various techniques, each suited for different levels of precision and computational resources. Here, we explore some common methods:
- Prime Factorization:
Using prime factorization simplifies the square root by breaking down the number into its prime factors:
- Find the prime factors of 5000:
\[
5000 = 2^3 \times 5^4
\]
- Use the properties of square roots to simplify:
\[
\sqrt{5000} = \sqrt{2^3 \times 5^4} = \sqrt{8 \times 625} = \sqrt{8} \times \sqrt{625} = 2 \sqrt{2} \times 25 = 50 \sqrt{2}
\]
This method is effective for exact simplification.
- Find the prime factors of 5000:
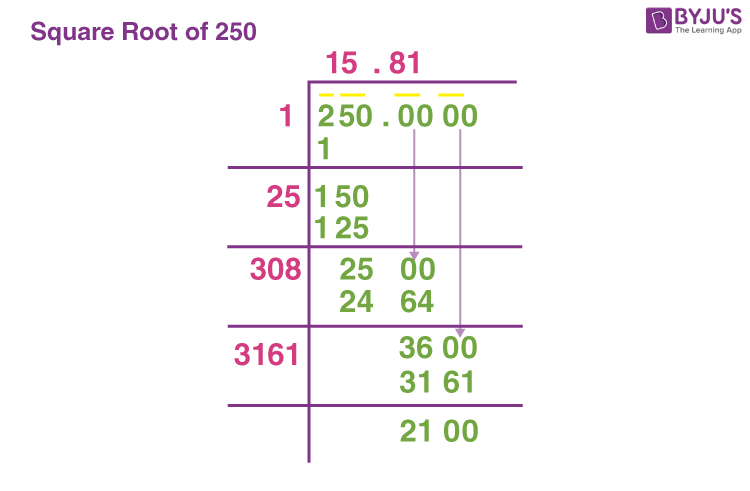
- Long Division Method:
The long division method provides a manual way to calculate the square root with high precision:
- Pair the digits of 5000 from right to left: \(50|00\).
- Find the largest number \( x \) whose square is less than or equal to the first pair (50):
\[
x = 7 \quad \text{because} \quad 7^2 = 49
\]
- Subtract \( 49 \) from \( 50 \), bring down the next pair (00) to get \( 100 \).
- Double the current quotient (7) to get 14, and find \( y \) such that \( 14y \times y \) is less than or equal to \( 100 \):
\[
y = 0 \quad \text{because} \quad 140 \times 0 = 0
\]
- Continue the process to get more decimal places as needed.
This method provides a step-by-step approach to finding square roots manually.
- Newton's Method (Heron's Method):
Newton's Method is an iterative technique for finding better approximations:
- Start with an initial guess \( x_0 \), e.g., \( x_0 = 70 \).
- Use the formula:
\[
x_{n+1} = \frac{1}{2} \left( x_n + \frac{5000}{x_n} \right)
\]
- Repeat until \( x_n \) converges. For example:
\[
x_1 = \frac{1}{2} \left( 70 + \frac{5000}{70} \right) \approx 70.714
\]
Continue until the desired accuracy is reached.
Newton's Method converges rapidly to the square root.
- Using Calculators:
Modern calculators provide a straightforward way to compute square roots. Simply input the number and press the square root function to obtain:
\[
\sqrt{5000} \approx 70.7107
\]
This method is convenient and efficient for quick calculations. - Approximation Techniques:
For quick estimates, you can use approximation methods:
- Identify two perfect squares close to 5000, such as 4900 (702) and 5041 (712).
- Since 5000 is closer to 5041, approximate \( \sqrt{5000} \) as slightly less than 71.
Approximations are useful for mental math or rough estimates.
These techniques demonstrate various approaches to calculating square roots, each suitable for different scenarios and levels of precision.
Calculating with Calculators and Software
When calculating the square root of 5000 using calculators or software, it's important to ensure accuracy and efficiency. Most scientific calculators have built-in functions for square roots, which can be accessed easily:
- Enter the number 5000 on your calculator.
- Look for the square root symbol (√) button on your calculator.
- Press the square root button to compute the square root of 5000.
Alternatively, if you're using software or an online calculator:
- Open the calculator application or website.
- Enter "sqrt(5000)" into the calculation area.
- Press the equals (=) button or hit enter to get the result.
Calculators and software typically provide the result of the square root of 5000 instantly and accurately, making them convenient tools for mathematical computations.

Frequently Asked Questions
Here are some common questions about the square root of 5000:
- What is the exact value of √5000?
- How can I calculate √5000 without a calculator?
- Is √5000 a rational or irrational number?
- What are the practical uses of knowing the square root of 5000?
- How many decimal places should I consider for √5000?
The exact value of √5000 is approximately 70.7106781187.
Calculating √5000 without a calculator involves using approximation methods such as the Babylonian method or using logarithms.
√5000 is an irrational number because it cannot be expressed as a simple fraction.
Knowing the square root of 5000 is useful in various fields such as engineering, physics, and finance for calculations involving area, volume, and estimation.
Depending on the application, it's often sufficient to consider √5000 to at least three decimal places for most practical purposes.
Tables and Charts
Below is a table showing the square root of 5000 to various decimal places:
| Decimal Places | Square Root of 5000 |
|---|---|
| 1 | 70.7 |
| 2 | 70.71 |
| 3 | 70.711 |
| 4 | 70.7107 |
| 5 | 70.71068 |
Additionally, here is a chart visually representing the square root of 5000:

Xét đoạn video '5000 cần phải chia cho số nhỏ nhất nào để nó trở thành một số mũ. #PhânTíchToánHọc'.
By which least number should 5000 be divided so that it becomes a perfect square | Maths Analysis
READ MORE:
Xem video 'Tính căn bậc hai của 5000 bằng tiếng Hindi | Vargmul Nikalna | Surendra Khilery'.
Square Root Of 5000 In Hindi | Tính căn bậc hai của 5000 | Surendra Khilery