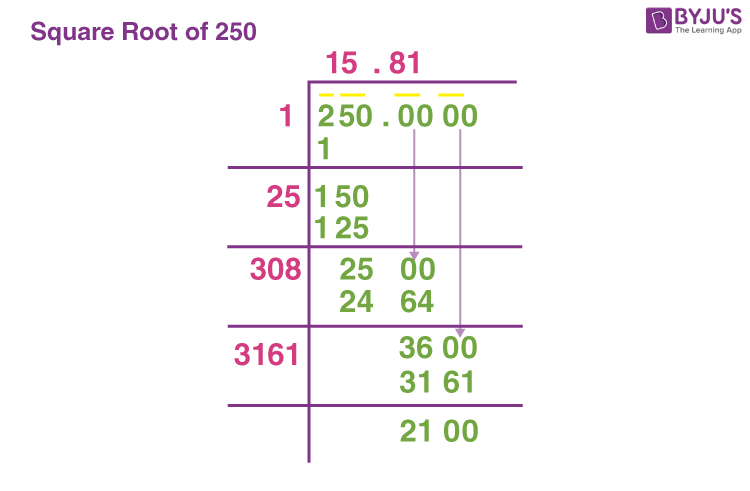
Topic 10 root 2 squared: Understanding and simplifying square roots is crucial in mathematics. The expression "10 root 2 squared" might seem complex, but breaking it down reveals simple concepts of exponents and radicals. This article explores methods to simplify square roots, the properties of square numbers, and practical examples to enhance your mathematical skills.
Table of Content
- Understanding "10 root 2 squared"
- Introduction to Square Roots and Squared Values
- Mathematical Definition and Calculation of Square Roots
- Properties of Perfect and Imperfect Squares
- Examples of Square Root Calculations
- Understanding and Simplifying Square Roots
- Applications of Square Roots in Algebra
- Methods for Finding Square Roots
- Square Root Symbol and Notation
- Calculators and Tools for Square Roots
- Common Problems and Solutions Involving Square Roots
- Square Roots in Real Numbers and Complex Numbers
- Tips for Remembering Perfect Squares
- Visual Representation of Square Roots
- FAQs About Square Roots and Squaring Numbers
- YOUTUBE: Xem video về giá trị của các số bình phương trong 2 giây để hiểu rõ hơn về từ khoá '10 căn bậc 2'.
Understanding "10 root 2 squared"
To understand the expression "10 root 2 squared", we need to break it down into its mathematical components and operations. Here is a detailed breakdown:
Breaking Down the Expression
- Root: The square root function, typically represented as √, finds a number that, when multiplied by itself, equals the original number. For example, √2 is approximately 1.414.
- Squared: Squaring a number means multiplying it by itself. For instance, 2 squared (2^2) is 4.
- 10 root 2: This can be interpreted as 10 times the square root of 2 (10 * √2).
- 10 root 2 squared: To square the entire expression, we take (10 * √2) and square it.
Step-by-Step Calculation
- First, find the square root of 2 (√2). The square root of 2 is approximately 1.414.
- Multiply this result by 10:
10 * √2 ≈ 10 * 1.414 ≈ 14.14
- Now, square the result of 10 * √2:
(10 * √2)^2 = (14.14)^2 ≈ 200
Therefore, (10 * √2)^2 is equal to 200.
Properties of Square Roots and Squares
Square roots and squares have some interesting properties:
- The square of a square root of a number returns the original number (e.g., (√a)^2 = a).
- When multiplying square roots, you can combine them under a single square root (e.g., √a * √b = √(a * b)).
- Squaring a product involves squaring each factor individually (e.g., (a * b)^2 = a^2 * b^2).
Examples of Square Roots and Squaring
| Number | Square Root | Square |
|---|---|---|
| 2 | √2 ≈ 1.414 | 2^2 = 4 |
| 3 | √3 ≈ 1.732 | 3^2 = 9 |
| 4 | √4 = 2 | 4^2 = 16 |
| 10 | √10 ≈ 3.162 | 10^2 = 100 |
Understanding how to manipulate and calculate expressions involving square roots and squares is essential for solving various mathematical problems.
READ MORE:
Introduction to Square Roots and Squared Values
Understanding square roots and squared values is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5, because \(5 \times 5 = 25\). The notation for the square root is the radical symbol \( \sqrt{} \). Squaring a number means multiplying it by itself. For instance, \( 3^2 = 3 \times 3 = 9 \).
Here are some essential points to help you understand square roots and squared values better:
- Principal Square Root: This refers to the non-negative square root of a number. For example, the principal square root of 9 is 3, denoted as \( \sqrt{9} = 3 \).
- Negative Roots: Every positive number actually has two square roots: one positive and one negative. For instance, the square roots of 25 are 5 and -5, since both \( 5^2 \) and \( (-5)^2 \) equal 25. However, the principal square root is the non-negative root.
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are integers.
- Calculating Square Roots: For non-perfect squares, we use approximations or calculators. For example, \( \sqrt{10} \approx 3.162 \).
Understanding these concepts is crucial for solving various mathematical problems and for applications in science, engineering, and beyond. As you continue to explore, you'll find that square roots and squared values are not only foundational but also incredibly useful in more advanced mathematics.
Mathematical Definition and Calculation of Square Roots
Understanding square roots is essential in mathematics. A square root of a number \(x\) is a value \(r\) such that \(r^2 = x\). The principal square root, denoted by the radical symbol \(\sqrt{}\), refers to the nonnegative root. For instance, \(\sqrt{9} = 3\) because \(3^2 = 9\).
Here are the steps to calculate square roots:
- Identify the number: Determine the number for which you need the square root.
- Perfect Squares: Check if the number is a perfect square (e.g., 4, 9, 16). For perfect squares, the square root is an integer (e.g., \(\sqrt{16} = 4\)).
- Prime Factorization: For non-perfect squares, break down the number into its prime factors. Use the property \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\).
- Simplify: Simplify the square root by combining pairs of prime factors.
- Approximation: If an exact value is not possible, use a calculator for approximation (e.g., \(\sqrt{10} \approx 3.162\)).
Example calculations:
- \(\sqrt{25} = 5\)
- \(\sqrt{45} = \sqrt{(9 \times 5)} = 3\sqrt{5}\)
- \(\sqrt{50} = \sqrt{(25 \times 2)} = 5\sqrt{2}\)
Understanding square roots involves recognizing their properties and applying methods to simplify and approximate values.
Properties of Perfect and Imperfect Squares
Understanding the properties of perfect and imperfect squares is fundamental in mathematics. These concepts help in simplifying calculations, solving equations, and understanding numerical relationships.
Perfect squares are the product of an integer multiplied by itself. They have distinct properties and patterns. Imperfect squares, on the other hand, are not the product of an integer by itself and often result in irrational numbers when their square roots are taken.
- Perfect Squares:
- Definition: A number that can be expressed as the square of an integer, e.g., \(1, 4, 9, 16, 25\).
- Properties:
- Always positive.
- Have an integer square root.
- The square root of a perfect square is always a whole number, e.g., \(\sqrt{16} = 4\).
- Even perfect squares are the square of even numbers, and odd perfect squares are the square of odd numbers.
- Imperfect Squares:
- Definition: A number that cannot be expressed as the square of an integer, e.g., \(2, 3, 5, 7, 8\).
- Properties:
- Can be positive or negative.
- Do not have an integer square root.
- The square root of an imperfect square is an irrational number, e.g., \(\sqrt{2} \approx 1.414\).
- When squared, these numbers do not produce integers.
These properties are essential in various mathematical applications, including solving quadratic equations, simplifying radical expressions, and analyzing numerical patterns.
Examples of Square Root Calculations
Calculating square roots involves finding a number that, when multiplied by itself, equals the original number. Here are some examples of square root calculations:
Example 1: Perfect Square
Calculate the square root of 16:
\[ \sqrt{16} = 4 \]
This is because \( 4 \times 4 = 16 \).
Example 2: Imperfect Square
Calculate the square root of 20:
\[ \sqrt{20} \approx 4.472 \]
This can be approximated using a calculator.
Example 3: Using Prime Factorization
Calculate the square root of 72 using prime factorization:
- 72 = 2 × 2 × 2 × 3 × 3
- Pair the primes: (2 × 2) and (3 × 3)
- Take one number from each pair: 2 and 3
- Multiply the results: \( 2 \times 3 = 6 \)
\[ \sqrt{72} = 6\sqrt{2} \]
Example 4: Simplifying Square Roots
Simplify the square root of 50:
- 50 = 2 × 5 × 5
- Take the square root of the perfect square part: \( \sqrt{5 \times 5} = 5 \)
- So, \[ \sqrt{50} = 5\sqrt{2} \]
Example 5: Square Root of a Fraction
Calculate the square root of \(\frac{9}{16}\):
\[ \sqrt{\frac{9}{16}} = \frac{\sqrt{9}}{\sqrt{16}} = \frac{3}{4} \]
Example 6: Using the Square Root Property
Calculate the square root of 81:
\[ \sqrt{81} = 9 \]
This is because \( 9 \times 9 = 81 \).
Example 7: Using a Calculator
Calculate the square root of 2 using a calculator:
\[ \sqrt{2} \approx 1.414 \]
Example 8: Complex Numbers
Calculate the square root of -1:
\[ \sqrt{-1} = i \]
where \( i \) is the imaginary unit.
Example 9: Square Root of Decimal Numbers
Calculate the square root of 0.25:
\[ \sqrt{0.25} = 0.5 \]
Example 10: Using the Exponent Method
Calculate the square root of 36 using exponents:
\[ 36^{0.5} = 6 \]
This is because \( 6 \times 6 = 36 \).

Understanding and Simplifying Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3 because \(3 \times 3 = 9\). Here, we'll explore how to understand and simplify square roots.
Basic Properties of Square Roots
- Every positive number has two square roots: one positive and one negative. For example, the square roots of 25 are 5 and -5.
- The principal square root is the non-negative root and is denoted by the radical symbol \(\sqrt{}\).
- Square roots of perfect squares (e.g., 1, 4, 9, 16) are integers.
Simplifying Square Roots
To simplify a square root, factor the number inside the radical into its prime factors and then apply the square root to each factor.
- Identify Perfect Squares: Factor the number under the square root into a product of two factors, one of which should be a perfect square if possible.
- Example: \(\sqrt{12}\) can be factored into \(\sqrt{4 \times 3}\).
- Apply the Square Root to Each Factor: Use the property \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\).
- Example: \(\sqrt{12} = \sqrt{4 \times 3} = \sqrt{4} \times \sqrt{3} = 2\sqrt{3}\).
Examples of Simplification
| Original Expression | Factorization | Simplified Form |
|---|---|---|
| \(\sqrt{45}\) | \(45 = 9 \times 5\) | \(\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}\) |
| \(\sqrt{50}\) | \(50 = 25 \times 2\) | \(\sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2}\) |
| \(\sqrt{72}\) | \(72 = 36 \times 2\) | \(\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}\) |
Rationalizing the Denominator
Sometimes, it's necessary to simplify expressions that have a square root in the denominator.
- Multiply the numerator and the denominator by the square root found in the denominator to eliminate the radical from the denominator.
- Simplify the resulting expression.
- Example: \(\frac{10}{\sqrt{2}}\).
- Multiply by \(\frac{\sqrt{2}}{\sqrt{2}}\): \(\frac{10}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{10\sqrt{2}}{2} = 5\sqrt{2}\).
- Example: \(\frac{10}{\sqrt{2}}\).
Understanding these principles can make working with square roots much easier and help simplify complex expressions.
Applications of Square Roots in Algebra
Square roots are fundamental in algebra and have a wide range of applications. Below are several key areas where square roots are used:
Solving Quadratic Equations
One of the most common applications of square roots in algebra is solving quadratic equations. The quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
relies on calculating the square root of the discriminant \( b^2 - 4ac \). This helps determine the roots of the quadratic equation \( ax^2 + b^2 + c = 0 \).
Pythagorean Theorem
Square roots are crucial in geometry, particularly in the Pythagorean theorem. For a right-angled triangle with sides \(a\), \(b\), and hypotenuse \(c\), the theorem states:
\[ c = \sqrt{a^2 + b^2} \]
This formula allows us to find the length of the hypotenuse if the lengths of the other two sides are known.
Distance Formula
The distance formula, used to find the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in the coordinate plane, involves square roots:
\[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. It is calculated using the square root of the variance:
\[ \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2} \]
where \( \sigma \) is the standard deviation, \( N \) is the number of values, \( x_i \) is each individual value, and \( \mu \) is the mean of the values.
Eigenvalues and Eigenvectors
In linear algebra, square roots appear in the process of finding eigenvalues and eigenvectors of matrices. The characteristic equation of a matrix often leads to a polynomial equation, where the roots, including square roots, determine the eigenvalues.
Examples of Applications
- Geometry - Calculating Diagonal Lengths: In geometry, expressions like \(2\sqrt{10}\) squared are used to find the length of a diagonal in a rectangle or square, illustrating the Pythagorean theorem in action.
- Physics - Kinematics: The equation for the time of flight of a projectile includes square roots. For example, the time \(t\) of a projectile launched with initial velocity \(v_0\) at an angle \(\theta\) is given by \( t = \frac{v_0 \sin \theta}{g} \), where \( g \) is the acceleration due to gravity.
Practice Problems
- Calculate the roots of the quadratic equation \( x^2 - 4x + 4 = 0 \).
- Find the length of the hypotenuse of a right-angled triangle with legs 6 and 8 units long.
- Determine the distance between the points (3, 4) and (7, 1) in the coordinate plane.
- Compute the standard deviation for the data set {2, 4, 4, 4, 5, 5, 7, 9}.
- Simplify and evaluate \(2\sqrt{10}\) squared.
Methods for Finding Square Roots
Finding the square root of a number can be accomplished through various methods. Here, we explore several common techniques, including the prime factorization method, the long division method, and estimation methods.
Prime Factorization Method
This method is suitable for finding the square roots of perfect squares. To use this method, we factor the number into its prime factors and pair them.
- Example: Find the square root of 81.
- Factorize 81: \(81 = 3 \times 3 \times 3 \times 3\).
- Pair the factors: \((3 \times 3) \times (3 \times 3) = 9 \times 9\).
- Take one number from each pair: \(\sqrt{81} = 9\).
- Example: Find the square root of 625.
- Factorize 625: \(625 = 5 \times 5 \times 5 \times 5\).
- Pair the factors: \((5 \times 5) \times (5 \times 5) = 25 \times 25\).
- Take one number from each pair: \(\sqrt{625} = 25\).
Long Division Method
This method is used for finding square roots of non-perfect squares or larger numbers. It is a more systematic approach that provides an accurate result.
- Example: Find the square root of 7921.
- Step 1: Pair the digits from right: \(79\) and \(21\).
- Step 2: Find the largest number whose square is less than or equal to the first pair: \(8^2 = 64\).
- Step 3: Subtract and bring down the next pair: \(79 - 64 = 15\), bring down 21 to get 1521.
- Step 4: Double the quotient and find the next digit: \(16\_ \times 9 = 1521\).
- Step 5: The quotient 89 is the square root: \(\sqrt{7921} = 89\).
- Example: Find the square root of 5.
- Step 1: Write 5 as 5.000000.
- Step 2: Find the largest number whose square is less than 5: \(2^2 = 4\).
- Step 3: Subtract and bring down pairs of zeros: \(5 - 4 = 1.00\).
- Step 4: Double the quotient and find the next digit: \(2 \times 2\_ = 4\_ \times 2 = 84\).
- Step 5: Continue the process to get: \(\sqrt{5} \approx 2.236\).
Estimation Methods
Estimation methods provide quick approximations and can be useful for mental calculations or when precision is not critical.
- Example: Estimate \(\sqrt{10}\)
- Recognize that \(3^2 = 9\) and \(4^2 = 16\), so \(\sqrt{10}\) is between 3 and 4.
- Refine the guess: \(3.1^2 = 9.61\) and \(3.2^2 = 10.24\).
- Further refine: \(3.16^2 \approx 10\).
- Thus, \(\sqrt{10} \approx 3.16\).
Square Root Symbol and Notation
The square root symbol is denoted by √ and is also known as the radical symbol. It is used to represent the square root of a number, which is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is represented as √9, which equals 3.
Here are some key terms associated with square roots:
- Radical Symbol: The symbol √ used to denote the square root.
- Radicand: The number under the radical symbol. For example, in √16, 16 is the radicand.
Square roots are important in mathematics and are used in various calculations. The notation is straightforward and follows these principles:
- The square root of a number 'a' is written as √a.
- The expression √a represents the principal (non-negative) square root of 'a'.
- The principal square root of 'a' is the positive number whose square is 'a'.
Let's look at some examples to understand how to use the square root symbol:
- Square Root of Perfect Squares:
- √25 = 5 because 52 = 25.
- √100 = 10 because 102 = 100.
- Square Root of Non-Perfect Squares:
- √2 ≈ 1.414 because 1.4142 ≈ 2.
- √10 ≈ 3.162 because 3.1622 ≈ 10.
It is important to remember that the square root symbol always refers to the principal square root, which is the non-negative root. For example, while both 52 and (-5)2 are 25, √25 only equals 5, not -5.
In algebra, the square root symbol is used in various operations and equations. Here are some examples:
- √4x = 2 implies that 4x = 4, so x = 1.
- x2 = 9 has two solutions: x = 3 and x = -3, but √x2 = |x|.
The square root symbol is also used in different contexts, such as geometry, where it can represent the length of a side of a square given its area, and in calculus, where it is involved in various functions and limits.
Understanding the proper usage and notation of square roots is crucial for solving mathematical problems efficiently. By mastering the symbol and its properties, you can handle more complex equations and mathematical concepts with confidence.

Calculators and Tools for Square Roots
Calculating square roots can be challenging without the right tools. Thankfully, there are several calculators and online tools available to simplify this process. Below are some of the best options you can use to find square roots efficiently:
-
Mathway Square Root Calculator
This tool allows you to enter any number and find its square root. It provides both exact forms and decimal approximations. You can visit their website or download the app for easier access.
-
Omni Calculator
Omni Calculator offers a detailed square root calculator that not only calculates square roots but also shows the simplification process. It's an excellent resource for understanding the steps involved in finding square roots.
-
Good Calculators
This website features a variety of mathematical calculators, including a square root calculator. It provides quick and accurate results and is very user-friendly.
-
Math.net Square Root Calculator
Math.net offers a simple and effective square root calculator. It's a great tool for students and anyone needing quick calculations. The site also provides educational resources for deeper understanding.
Using Square Root Calculators
Here is a step-by-step guide to using these calculators:
- Enter the Number: Input the number for which you need to find the square root. Ensure it is a non-negative real number.
- Submit the Query: Click the "Calculate" button or equivalent to process your input.
- View Results: The calculator will display the square root. For non-perfect squares, it will often show both the exact form and a decimal approximation.
- Analyze the Steps (if available): Some calculators, like Omni Calculator, show the step-by-step process of how the square root was simplified, which is excellent for learning purposes.
Examples
| Number | Square Root | Explanation |
|---|---|---|
| 25 | 5 | 25 is a perfect square (52 = 25). |
| 27 | 3√3 | Simplified by finding the factors: 27 = 9 × 3. √27 = √(9 × 3) = 3√3. |
| 144 | 12 | 144 is a perfect square (122 = 144). |
These calculators not only provide answers but also help you understand the process, making them valuable educational tools. Whether for academic purposes or practical applications, using these tools can significantly simplify your work with square roots.
Common Problems and Solutions Involving Square Roots
Understanding square roots and solving problems involving them can sometimes be challenging. Here are some common issues students encounter and step-by-step solutions to address them:
-
Problem 1: Simplifying Square Roots
Simplify \( \sqrt{50} \).
- Factor the number under the square root into prime factors: \( 50 = 2 \times 5^2 \).
- Rewrite using the property of square roots: \( \sqrt{50} = \sqrt{2 \times 5^2} \).
- Separate the factors under the square root: \( \sqrt{50} = \sqrt{2} \times \sqrt{5^2} \).
- Simplify: \( \sqrt{5^2} = 5 \), so \( \sqrt{50} = 5\sqrt{2} \).
-
Problem 2: Solving Equations with Square Roots
Solve \( \sqrt{x} + 3 = 7 \).
- Isolate the square root: \( \sqrt{x} = 7 - 3 \).
- Simplify: \( \sqrt{x} = 4 \).
- Square both sides to eliminate the square root: \( x = 4^2 \).
- Simplify: \( x = 16 \).
-
Problem 3: Finding the Square Root Using Prime Factorization
Find the square root of \( 144 \) using prime factorization.
- Factor \( 144 \) into its prime factors: \( 144 = 2^4 \times 3^2 \).
- Write the square root expression: \( \sqrt{144} = \sqrt{2^4 \times 3^2} \).
- Apply the property of square roots: \( \sqrt{144} = \sqrt{2^4} \times \sqrt{3^2} \).
- Simplify: \( \sqrt{2^4} = 2^2 = 4 \) and \( \sqrt{3^2} = 3 \), so \( \sqrt{144} = 4 \times 3 = 12 \).
-
Problem 4: Solving Quadratic Equations by Completing the Square
Solve \( x^2 + 6x + 9 = 25 \) by completing the square.
- Move the constant term to the other side: \( x^2 + 6x = 25 - 9 \).
- Simplify: \( x^2 + 6x = 16 \).
- Complete the square on the left side: \( x^2 + 6x + 9 = 16 + 9 \).
- Rewrite the equation: \( (x + 3)^2 = 25 \).
- Take the square root of both sides: \( x + 3 = \pm 5 \).
- Solve for \( x \): \( x = 5 - 3 \) or \( x = -5 - 3 \), so \( x = 2 \) or \( x = -8 \).
-
Problem 5: Solving Square Root Equations with Variables on Both Sides
Solve \( \sqrt{x + 2} = x - 2 \).
- Square both sides to eliminate the square root: \( x + 2 = (x - 2)^2 \).
- Expand the right side: \( x + 2 = x^2 - 4x + 4 \).
- Move all terms to one side: \( x^2 - 5x + 2 = 0 \).
- Solve the quadratic equation using the quadratic formula: \( x = \frac{5 \pm \sqrt{25 - 8}}{2} \).
- Simplify: \( x = \frac{5 \pm \sqrt{17}}{2} \).
Square Roots in Real Numbers and Complex Numbers
The concept of square roots can be extended beyond the set of real numbers to include complex numbers. This allows us to handle the square roots of negative numbers, which are not defined in the real number system.
Square Roots in Real Numbers
In the set of real numbers, the square root of a non-negative number \( x \) is a number \( y \) such that \( y^2 = x \). For example:
- \(\sqrt{4} = 2\) because \(2^2 = 4\)
- \(\sqrt{9} = 3\) because \(3^2 = 9\)
Real numbers do not have square roots for negative values because no real number squared results in a negative value. For example, there is no real number \( y \) such that \( y^2 = -1 \).
Square Roots in Complex Numbers
To address the square roots of negative numbers, we use complex numbers. A complex number is of the form \( a + bi \), where \( a \) and \( b \) are real numbers and \( i \) is the imaginary unit, defined by \( i = \sqrt{-1} \). Using \( i \), we can define the square roots of negative numbers. For example:
- \(\sqrt{-1} = i\)
- \(\sqrt{-4} = 2i\) because \((2i)^2 = 4i^2 = 4(-1) = -4\)
Calculations Involving Complex Numbers
Consider the square root of \(-6\) multiplied by the square root of \(-15\):
\[
\sqrt{-6} \cdot \sqrt{-15} = i\sqrt{6} \cdot i\sqrt{15} = i^2 \sqrt{90} = -\sqrt{90} = -3\sqrt{10}
\]
This illustrates that the product of two square roots of negative numbers results in a real number.
Real and Complex Solutions
When solving quadratic equations, the solutions may be real or complex depending on the discriminant \( b^2 - 4ac \). For example, the equation \( x^2 + 1 = 0 \) has no real solutions, but has complex solutions \( x = i \) and \( x = -i \).
Key Points
- The imaginary unit \( i \) is defined as \( i = \sqrt{-1} \) and \( i^2 = -1 \).
- Complex numbers extend the real number system to include solutions to the square roots of negative numbers.
- Operations with complex numbers follow the same algebraic rules as real numbers, with the addition of \( i \).
Understanding square roots in both real and complex numbers is essential for solving a wide range of mathematical problems, especially those involving quadratic equations and other polynomial functions.
Tips for Remembering Perfect Squares
Remembering perfect squares can be simplified with some tips and tricks. Here are several methods to help you quickly recall perfect squares:
-
Recognize patterns:
- Numbers ending in 0 have perfect squares ending in 00. For example, \(10^2 = 100\).
- Numbers ending in 5 have perfect squares ending in 25. For instance, \(15^2 = 225\).
- Numbers ending in 1 or 9 have perfect squares ending in 1. For example, \(11^2 = 121\) and \(19^2 = 361\).
-
Use visual aids:
Visualize numbers on a grid. The square of a number corresponds to the area of a square. For instance, the square of 4 is 16, which can be visualized as a 4x4 grid.
-
Memorize common perfect squares:
- \(1^2 = 1\)
- \(2^2 = 4\)
- \(3^2 = 9\)
- \(4^2 = 16\)
- \(5^2 = 25\)
- \(6^2 = 36\)
- \(7^2 = 49\)
- \(8^2 = 64\)
- \(9^2 = 81\)
- \(10^2 = 100\)
-
Use multiplication shortcuts:
For numbers ending in 5, use the formula: if the number is \(n5\), then the square is \((n \cdot (n + 1)) \cdot 100 + 25\). For example, \(25^2 = (2 \cdot 3) \cdot 100 + 25 = 625\).
-
Practice regularly:
Regular practice and testing yourself on perfect squares can help reinforce memory. Use flashcards or apps designed for math practice.

Visual Representation of Square Roots
Visualizing square roots can be insightful for understanding their properties and relationships. Here are some visual representations:
- Number Line: Plotting square roots on a number line helps to see their positions relative to other numbers.
- Geometric Shapes: Squares with sides corresponding to square roots demonstrate the area concept associated with square roots.
- Graphs: Graphical representations of functions involving square roots, such as y = √x, illustrate the curve formed.
- Pythagorean Theorem: Using triangles to illustrate relationships between square roots and sides can provide geometric insights.
- Color Coding: Visualizing square roots with different colors in data sets or charts can aid in comprehension.
FAQs About Square Roots and Squaring Numbers
- What is a square root?
A square root of a number is a value that, when multiplied by itself, gives the original number.
- How do you calculate a square root?
The square root of a number can be found using various methods such as estimation, factorization, or using a calculator.
- What is the difference between perfect squares and imperfect squares?
Perfect squares are numbers that can be expressed as the square of an integer (e.g., 4, 9, 16), while imperfect squares are numbers that are not perfect squares (e.g., 5, 10, 13).
- What are some real-world applications of square roots?
Square roots are used in fields such as engineering, physics, and finance for calculations involving area, volume, and risk assessment.
- How can square roots be visualized?
Visual representations of square roots include number lines, geometric shapes like squares, graphs of functions, and color-coded data sets.
- Why is squaring a number important?
Squaring a number is important for calculating areas of squares and rectangles, determining distances in geometry, and solving quadratic equations.
Xem video về giá trị của các số bình phương trong 2 giây để hiểu rõ hơn về từ khoá '10 căn bậc 2'.
Giá trị của Các Số Bình Phương trong 2 Giây - Video Hấp Dẫn
READ MORE:
Xem cách đơn giản hóa biểu thức căn bậc hai bình phương để tăng hiểu biết về từ khoá '10 căn bậc 2'.
Đơn giản hóa biểu thức căn bậc hai bình phương