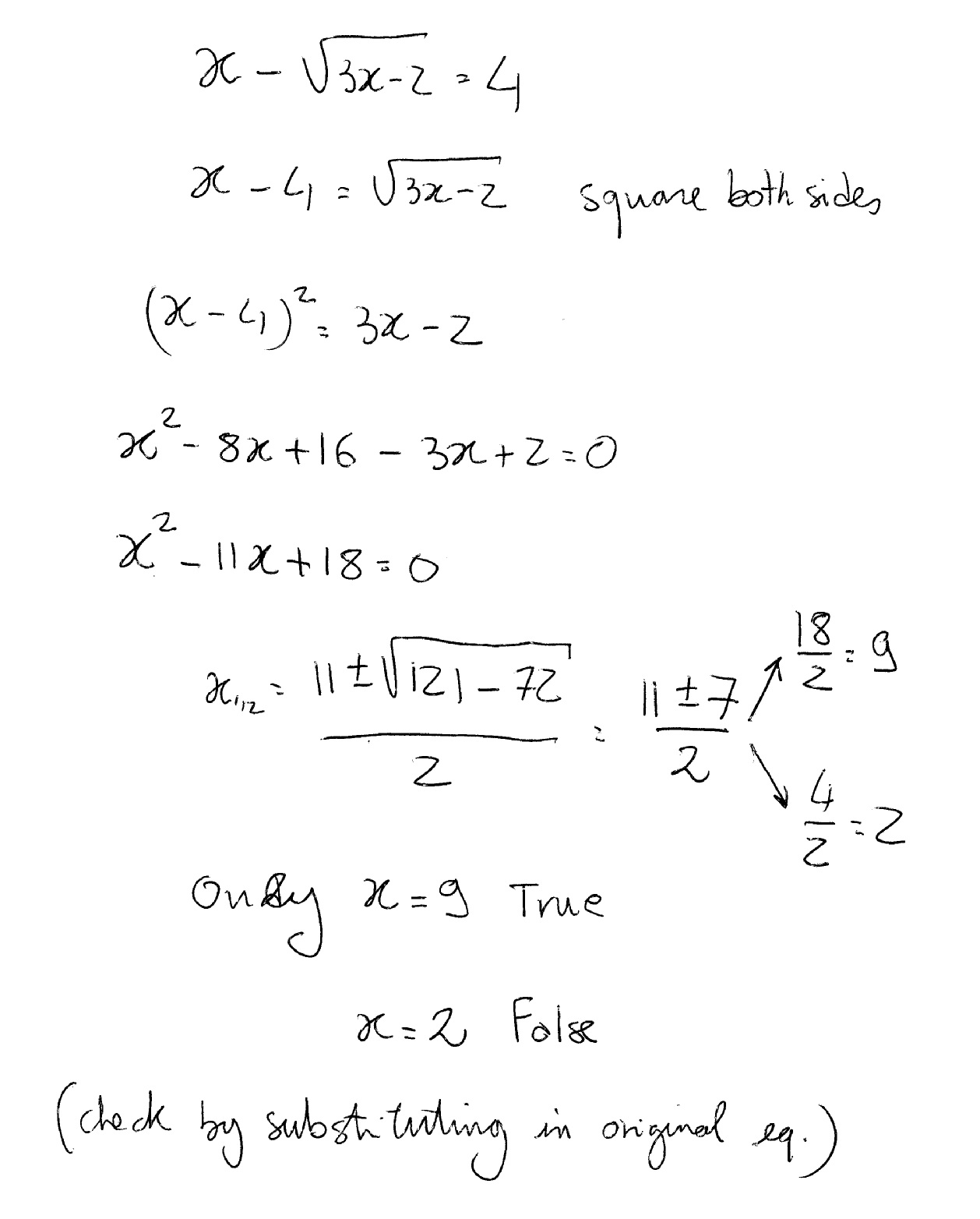Topic 2 square root of 5: The mathematical expression "2 square root of 5" often appears in algebra and calculus. In this article, we will explore its exact and decimal forms, simplification steps, and practical applications. Whether you are a student or a math enthusiast, understanding this concept is crucial for solving various mathematical problems efficiently.
Table of Content
- Simplifying and Understanding "2 √5"
- Introduction to Square Roots
- Basic Definitions and Properties
- Simplifying Square Roots
- Exact Form and Decimal Form
- Calculation Methods
- Common Examples and Problems
- Practical Applications of Square Roots
- Square Root Calculators and Tools
- Related Mathematical Concepts
- Advanced Topics
- YOUTUBE:
Simplifying and Understanding "2 √5"
The expression "2 √5" represents a number that is two times the square root of 5. This expression is often encountered in algebra and can be simplified or approximated depending on the context. Below are the steps and explanations on how to handle this expression mathematically.
Exact Form
The exact form of the expression "2 √5" cannot be simplified further since 5 is a prime number and does not have any square factors. Thus, the expression remains as it is.
Decimal Approximation
For practical purposes, we often convert "2 √5" to its decimal form:
\[ 2 \sqrt{5} \approx 2 \times 2.236 = 4.472 \]
Simplification Steps
- Identify the expression: \( 2 \sqrt{5} \)
- Since 5 is a prime number, the square root of 5 cannot be simplified further.
- Multiply 2 by the square root of 5 to get the decimal approximation.
Using a Calculator
To find the value of "2 √5" using a calculator, follow these steps:
- Enter 5 into the calculator.
- Press the square root (√) button to get the value of √5, which is approximately 2.236.
- Multiply this result by 2 to get the final approximation, which is about 4.472.
Mathematical Properties
- Nonnegative Real Numbers: Every nonnegative real number has a unique nonnegative square root, called the principal square root, denoted by √.
- Radical Sign: The symbol √ is called the radical sign or radix.
Understanding the properties and simplifications of square roots is essential for solving algebraic problems and performing calculations efficiently.
| Expression | Exact Form | Decimal Approximation |
|---|---|---|
| 2 √5 | 2 √5 | 4.472 |
For more detailed calculations and explanations, you can use online calculators and resources such as Mathway, Mathwarehouse, and Math is Fun.
READ MORE:
Introduction to Square Roots
Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, since 3 multiplied by 3 equals 9. The symbol for square root is √, and it is often used in various mathematical calculations and problem-solving scenarios.
The square root of a number can be found using several methods, including estimation, prime factorization, and the use of calculators. For perfect squares, such as 16 or 25, the square root is an integer. However, for non-perfect squares like 5, the square root is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal form is non-repeating and non-terminating.
Here are some important points about square roots:
- The square root of a product: √(a * b) = √a * √b
- The square root of a quotient: √(a / b) = √a / √b
- Square roots of negative numbers are not real numbers but are considered imaginary numbers in the complex number system.
- Perfect squares have exact square roots, while non-perfect squares have approximate square roots.
For example, to simplify the square root of 45:
- Factorize 45 into 9 and 5, so √45 = √(9 * 5).
- Use the rule √(a * b) = √a * √b, resulting in √9 * √5.
- Since √9 is 3, the expression simplifies to 3√5.
Calculating square roots by hand can be tedious for large numbers or non-perfect squares, so calculators are often used. The square root of 5, for example, is approximately 2.236. Understanding square roots is crucial for various fields such as engineering, physics, and finance, where they are used to solve quadratic equations, calculate areas, and determine statistical variances.
Basic Definitions and Properties
The concept of square roots is fundamental in mathematics. A square root of a number \(a\) is a value that, when multiplied by itself, gives \(a\). For instance, the square root of 25 is 5, since \(5 \times 5 = 25\). This is denoted as \(\sqrt{25} = 5\).
There are several important properties and definitions related to square roots:
- Principal Square Root: The non-negative square root of a non-negative number. For example, the principal square root of 9 is 3, denoted as \(\sqrt{9} = 3\).
- Perfect Squares: Numbers that are the square of an integer. Examples include 1, 4, 9, 16, 25, etc.
- Product Property: The square root of a product is the product of the square roots of the factors: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).
- Quotient Property: The square root of a quotient is the quotient of the square roots of the numerator and the denominator: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
These properties allow for the simplification of expressions involving square roots, such as \(\sqrt{45}\). By recognizing that 45 can be factored into 9 and 5, where 9 is a perfect square, we can simplify \(\sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} = 3\sqrt{5}\).
Furthermore, understanding these properties is essential for more advanced mathematical operations, including solving equations involving square roots and working with higher-order roots.
| Operation | Example | Result |
|---|---|---|
| Square Root of a Product | \(\sqrt{36 \times 25}\) | \(\sqrt{36} \times \sqrt{25} = 6 \times 5 = 30\) |
| Square Root of a Quotient | \(\sqrt{\frac{49}{16}}\) | \(\frac{\sqrt{49}}{\sqrt{16}} = \frac{7}{4}\) |
Simplifying Square Roots
Simplifying square roots involves reducing the expression under the square root to its simplest form. This process can make calculations easier and results more understandable. Here are the steps to simplify square roots:
- Identify factors of the number under the square root that are perfect squares.
- Rewrite the square root as a product of two square roots, separating the perfect square factors.
- Simplify the square root of the perfect square factor.
- Combine the simplified square root with the remaining square root.
Let's go through an example:
- Example: Simplify
- Factor 12 into 4 and 3:
- The square root of 4 is 2:
- Combine the results:
So, simplifies to .
Here's another example:
- Example: Simplify
- Factor 18 into 9 and 2:
- The square root of 9 is 3:
- Combine the results:
So, simplifies to .
Simplifying square roots can help in various mathematical problems, making equations easier to solve and expressions easier to understand.
Exact Form and Decimal Form
When working with square roots, it is important to distinguish between the exact form and the decimal form of the expression. The exact form retains the radical, providing a precise mathematical representation, whereas the decimal form offers an approximate numerical value.
Exact Form
The exact form of the expression \(2\sqrt{5}\) maintains the radical. This form is useful in algebraic manipulations and for conveying precise values in mathematical expressions.
For example, \(2\sqrt{5}\) remains in its radical form and can be used in equations and simplifications without approximating the value.
Decimal Form
The decimal form of \(2\sqrt{5}\) involves calculating the numerical value of the expression. To convert \(2\sqrt{5}\) into decimal form, you multiply the number 2 by the square root of 5, approximated to a certain number of decimal places.
The calculation is as follows:
- Calculate \(\sqrt{5} \approx 2.236\)
- Multiply by 2: \(2 \times 2.236 = 4.472\)
Thus, the decimal form of \(2\sqrt{5}\) is approximately 4.472.
Usage in Different Contexts
The choice between exact and decimal form depends on the context:
- Exact Form: Preferred in algebraic manipulations and when precise mathematical expressions are required.
- Decimal Form: Useful in practical applications where an approximate numerical value is sufficient or necessary.

Calculation Methods
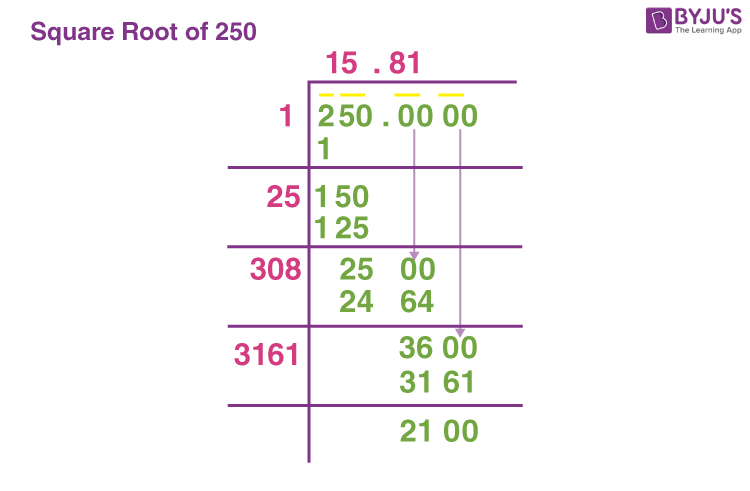
Calculating the value of expressions like \(2 \sqrt{5}\) can be done using different methods, including manual calculation and using calculators. Here, we will discuss both approaches.
- Manual Calculation:
- Start by understanding the square root function. The square root of a number \(n\) is a value that, when multiplied by itself, gives \(n\).
- For \(\sqrt{5}\), find an approximate value. We know that \(\sqrt{4} = 2\) and \(\sqrt{9} = 3\), so \(\sqrt{5}\) is between 2 and 3.
- Using estimation or the long division method, approximate \(\sqrt{5} \approx 2.236\).
- Multiply this approximation by 2 to get \(2 \times 2.236 \approx 4.472\).
- Using a Calculator:
- Enter the expression \(2 \sqrt{5}\) into a scientific calculator. Most calculators have a square root function that simplifies this process.
- Alternatively, use online calculators by inputting the expression directly. These tools provide both the exact form and the decimal approximation.
By using these methods, you can accurately determine the value of \(2 \sqrt{5}\). Whether you prefer manual calculations for a deeper understanding or a calculator for quick results, both are effective in finding the solution.
Common Examples and Problems
Understanding how to work with the expression "2 square root of 5" can be made easier by going through some common examples and problems. Here are a few to help illustrate various applications and methods of working with this expression:
Example 1: Simplifying Expressions
Simplify the expression \(2\sqrt{5} \times 3\sqrt{5}\).
Solution:
- First, multiply the coefficients: \(2 \times 3 = 6\).
- Next, multiply the square roots: \(\sqrt{5} \times \sqrt{5} = \sqrt{25} = 5\).
- Combine the results: \(6 \times 5 = 30\).
Thus, \(2\sqrt{5} \times 3\sqrt{5} = 30\).
Example 2: Adding and Subtracting Like Terms
Simplify the expression \(7\sqrt{5} + 2\sqrt{5}\).
Solution:
- Since the terms are like terms (both contain \(\sqrt{5}\)), simply add the coefficients: \(7 + 2 = 9\).
- Attach the common square root: \(9\sqrt{5}\).
Thus, \(7\sqrt{5} + 2\sqrt{5} = 9\sqrt{5}\).
Example 3: Rationalizing the Denominator
Simplify the expression \(\frac{4}{2\sqrt{5}}\).
Solution:
- Rationalize the denominator by multiplying the numerator and the denominator by \(\sqrt{5}\): \(\frac{4 \cdot \sqrt{5}}{2\sqrt{5} \cdot \sqrt{5}} = \frac{4\sqrt{5}}{2 \cdot 5}\).
- Simplify the fraction: \(\frac{4\sqrt{5}}{10} = \frac{2\sqrt{5}}{5}\).
Thus, \(\frac{4}{2\sqrt{5}} = \frac{2\sqrt{5}}{5}\).
Example 4: Solving Equations Involving Square Roots
Solve for \(x\): \(2\sqrt{5}x = 10\).
Solution:
- Isolate \(x\) by dividing both sides by \(2\sqrt{5}\): \(x = \frac{10}{2\sqrt{5}}\).
- Simplify the expression: \(x = \frac{10}{2\sqrt{5}} = \frac{5}{\sqrt{5}}\).
- Rationalize the denominator: \(x = \frac{5 \cdot \sqrt{5}}{\sqrt{5} \cdot \sqrt{5}} = \frac{5\sqrt{5}}{5} = \sqrt{5}\).
Thus, \(x = \sqrt{5}\).
Example 5: Word Problem Involving Square Roots
Suppose a square has an area of \(50 \, \text{square units}\). Find the length of one side of the square.
Solution:
- Let the side length of the square be \(s\). The area of a square is given by \(s^2\).
- Set up the equation: \(s^2 = 50\).
- Solve for \(s\): \(s = \sqrt{50} = \sqrt{25 \cdot 2} = \sqrt{25} \cdot \sqrt{2} = 5\sqrt{2}\).
Thus, the length of one side of the square is \(5\sqrt{2}\) units.
Practical Applications of Square Roots
Square roots, including expressions like \(2\sqrt{5}\), have numerous practical applications across various fields. Here are some detailed examples:
-
Geometry and Construction
In geometry, square roots are essential for calculating distances and dimensions. For instance, to find the diagonal of a square with a side length \(a\), we use \( \sqrt{2a^2} \). Similarly, in construction, square roots help in determining the correct lengths for materials. For example, if a patio has an area of 200 square feet, the side length of the square patio is \( \sqrt{200} \approx 14.1 \) feet.
-
Physics
In physics, square roots are used to determine various parameters such as the time it takes for an object to fall to the ground under gravity. The formula \( t = \frac{\sqrt{h}}{4} \) where \( h \) is the height in feet, helps calculate the fall time. For instance, an object dropped from a height of 64 feet will take \( \frac{\sqrt{64}}{4} = 2 \) seconds to reach the ground.
-
Finance
In finance, square roots are used to calculate stock market volatility. The standard deviation, which is a measure of volatility, is the square root of the variance of stock returns. This helps investors assess the risk of investments more accurately.
-
Statistics
Square roots are fundamental in statistical analysis, particularly in calculating the standard deviation, which is the square root of the variance. This measure helps in understanding the dispersion of data points from the mean, crucial for making informed decisions based on data.
-
Engineering
In engineering, square roots are used in calculations involving natural frequencies of structures to predict their behavior under different loads. For example, engineers might use square roots to ensure bridges can withstand strong winds or heavy traffic without excessive vibrations.
-
Computer Graphics
In computer graphics, square roots are used to calculate distances and transformations in 2D and 3D space. For example, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) is given by \( \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).
-
Navigation
Square roots are used in navigation to compute distances between points on a map. Pilots and sailors use these calculations to determine the shortest path and to estimate travel times accurately.
-
Accident Investigations
Police use square roots to determine the speed of vehicles from the length of skid marks. For example, if the skid mark length is \( d \) feet, the speed \( s \) can be calculated using the formula \( s = \sqrt{24d} \).
These examples demonstrate how square roots are an essential mathematical tool used in various real-world applications, helping to solve problems and make accurate calculations in diverse fields.
Square Root Calculators and Tools
Square root calculators are essential tools for students, teachers, and professionals to quickly find the square roots of numbers. These calculators can handle both simple and complex calculations, providing exact and decimal forms. Here are some popular and useful square root calculators:
-
Mathway Square Root Calculator
Mathway's Square Root Calculator allows users to enter a radical expression and find its square root. If the number is a perfect square, it provides an exact answer. For non-perfect squares, it offers both exact and decimal forms.
-
Omni Calculator
Omni Calculator not only calculates square roots but also helps in simplifying them. It identifies perfect square factors in the radicand, making it easy to break down complex expressions.
-
Good Calculators Square Root Calculator
This tool calculates the square roots of positive and negative numbers, including complex or imaginary solutions for negative radicands. It also determines if a number is a perfect square.
-
Calculator Soup Square Root Calculator
Calculator Soup provides a straightforward calculator for finding the principal square root of positive real numbers. It indicates whether the number is a perfect square and provides fractional exponents for more advanced calculations.
-
Math.net Square Root Calculator
Math.net offers a simple interface for calculating the principal square root of nonnegative real numbers, providing an educational overview of the concept alongside the calculator.
These calculators are valuable resources for anyone needing to perform quick and accurate square root calculations, from simple arithmetic to advanced mathematical problems.

Related Mathematical Concepts
The mathematical expression \(2\sqrt{5}\) connects with various related mathematical concepts, enhancing our understanding of both simple and complex topics in mathematics. Here are some key concepts related to \(2\sqrt{5}\):
1. Irrational Numbers
The value \(\sqrt{5}\) is an irrational number, meaning it cannot be exactly expressed as a fraction and its decimal representation is non-repeating and non-terminating. Therefore, \(2\sqrt{5}\) is also irrational. Understanding irrational numbers is crucial for grasping the nature of many mathematical expressions and their properties.
2. Simplifying Square Roots
Simplifying square roots involves expressing them in their simplest radical form. For example, \(\sqrt{20}\) can be simplified to \(2\sqrt{5}\) by recognizing that 20 is \(4 \times 5\), and \(\sqrt{4} = 2\). This technique is essential for working with radicals in algebraic expressions and equations.
3. Pythagorean Theorem
The Pythagorean theorem, \(a^2 + b^2 = c^2\), often involves square roots. In right triangles, the length of the hypotenuse can sometimes be an expression involving square roots, such as \(2\sqrt{5}\). This theorem is fundamental in geometry for calculating distances and constructing geometric shapes.
4. Radical Equations
Equations involving square roots, known as radical equations, require specific techniques to solve. For instance, solving \(2\sqrt{5x} = 10\) involves isolating the square root term and then squaring both sides to eliminate the radical, leading to further algebraic simplification.
5. Quadratic Equations
Quadratic equations of the form \(ax^2 + bx + c = 0\) can sometimes have solutions involving square roots, especially when using the quadratic formula, \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\). Understanding how to handle the square root term is crucial for finding the roots of such equations.
6. Complex Numbers
Square roots play a significant role in complex numbers, particularly when dealing with the imaginary unit \(i\), where \(i = \sqrt{-1}\). Expressions like \(2\sqrt{5}\) can appear in the real or imaginary parts of complex numbers, highlighting the connection between radicals and complex number theory.
7. Trigonometry
In trigonometry, square roots often appear in the context of trigonometric identities and formulas. For example, the exact values of sine and cosine for 45° (\(\pi/4\)) angles involve \(\sqrt{2}/2\). Understanding these relationships helps in solving trigonometric equations and analyzing wave functions.
8. Exponents and Logarithms
Square roots can also be expressed using fractional exponents, as \(2\sqrt{5}\) is equivalent to \(2 \cdot 5^{1/2}\). This representation is useful in calculus and higher algebra, where manipulating exponents and logarithms becomes necessary.
9. Mathematical Proofs
The properties of square roots and irrational numbers like \(2\sqrt{5}\) are often used in mathematical proofs. For example, proving the irrationality of \(\sqrt{5}\) involves showing that no rational number squared equals 5, which extends to the irrational nature of \(2\sqrt{5}\).
By exploring these related concepts, one gains a deeper appreciation of the interconnectedness of mathematical ideas and the foundational role that square roots play in various branches of mathematics.
Advanced Topics
In this section, we delve into more advanced concepts related to square roots, specifically focusing on the expression \(2 \sqrt{5}\). We'll explore its properties, applications in higher mathematics, and connections to other mathematical fields.
1. Properties of \(2 \sqrt{5}\)
- Irrationality: Since \(\sqrt{5}\) is an irrational number, \(2 \sqrt{5}\) is also irrational.
- Multiplicative Properties: The expression \(2 \sqrt{5}\) can be manipulated using properties of square roots, such as \((2 \sqrt{5})^2 = 4 \times 5 = 20\).
- Algebraic Manipulations: In algebraic expressions, \(2 \sqrt{5}\) can be combined with other terms, simplified, or used in equations.
2. Applications in Geometry
The term \(2 \sqrt{5}\) appears in various geometric contexts. For example:
- Diagonals of Rectangles: In a rectangle with sides of lengths \(a\) and \(b\), the diagonal length is given by \(\sqrt{a^2 + b^2}\). If the sides are \(2\) and \(\sqrt{20}\), the diagonal length is \(2 \sqrt{5}\).
- Pythagorean Theorem: When solving problems involving right triangles, \(2 \sqrt{5}\) can represent the length of one of the sides or the hypotenuse.
3. Connection to Algebraic Numbers
Algebraic numbers are roots of polynomial equations with integer coefficients. \(2 \sqrt{5}\) is related to the polynomial equation:
\[ x^2 - 20 = 0 \]
which has roots \(\pm 2 \sqrt{5}\).
4. Trigonometric Integrals
The expression \(2 \sqrt{5}\) can appear in integrals involving trigonometric functions. For instance:
\[ \int \sin(2 \sqrt{5} \, x) \, dx = -\frac{1}{2 \sqrt{5}} \cos(2 \sqrt{5} \, x) + C \]
5. Complex Numbers
In the context of complex numbers, \(2 \sqrt{5}\) can be used to represent magnitudes. For example, the magnitude of the complex number \(2 + 2i \sqrt{5}\) is given by:
\[ |2 + 2i \sqrt{5}| = \sqrt{2^2 + (2 \sqrt{5})^2} = \sqrt{4 + 20} = \sqrt{24} = 2 \sqrt{6} \]
6. Analytical Geometry
In analytical geometry, the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\) in the plane can involve \(2 \sqrt{5}\). For example, the distance formula:
\[ \text{Distance} = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
For points \((0, 0)\) and \((2, 2 \sqrt{5})\), the distance is:
\[ \sqrt{(2 - 0)^2 + (2 \sqrt{5} - 0)^2} = \sqrt{4 + 20} = \sqrt{24} = 2 \sqrt{6} \]
7. Fourier Series
In the study of Fourier series, \(2 \sqrt{5}\) can appear as a coefficient in the expansion of periodic functions. For example, in the series expansion of a function \(f(x)\), a term might be:
\[ a_n \cos\left(\frac{2 \pi n}{2 \sqrt{5}} x\right) \]
8. Quantum Mechanics
In quantum mechanics, wavefunctions can involve terms like \(2 \sqrt{5}\) in their normalization constants or potential energy functions. For example, a wavefunction might be normalized as:
\[ \psi(x) = \sqrt{\frac{2}{2 \sqrt{5}}} \sin(k x) \]
Căn bậc hai của 5 được đơn giản hóa
READ MORE:
Học cách đơn giản hóa căn bậc hai