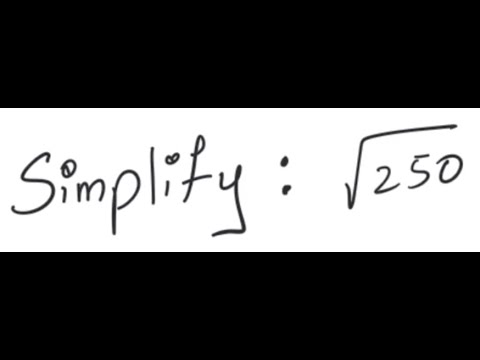Topic 3 x square root of 2: Explore the intriguing world of 3 × square root of 2 in this article. Understand its mathematical foundation, visualize its applications in geometry, and discover its relevance in real-life scenarios. Whether you're a math enthusiast or a curious learner, this journey through irrational numbers promises fascinating insights and practical knowledge.
Table of Content
- Understanding the Expression: 3 × √2
- Introduction to 3 × Square Root of 2
- Mathematical Explanation and Calculation
- Applications in Geometry
- Significance in Algebra and Trigonometry
- Visualization and Graphical Representation
- Properties of Irrational Numbers
- Examples and Real-Life Applications
- Comparison with Other Multiples of Square Roots
- Related Mathematical Concepts
- Conclusion and Summary
- YOUTUBE: Khám phá cách giải phương trình 1/3 nhân căn bậc hai của 2x = 2 và hiểu sâu hơn về nó. Nhiều người vẫn chưa hiểu đầy đủ điều này!
Understanding the Expression: 3 × √2
The expression 3 × \sqrt{2} appears in various contexts, from mathematical calculations to geometric interpretations. This section explores its significance and application.
Mathematical Definition
The expression 3 × \sqrt{2} represents a number that is three times the square root of 2. Mathematically, this can be written as:
\[ 3 \times \sqrt{2} \approx 3 \times 1.414 = 4.242 \]
This value is approximately 4.242, a result often used in calculations involving irrational numbers.
Properties and Applications
- Geometry: In geometry,
3 × \sqrt{2}can represent dimensions, such as the diagonal of a square whose sides are3\sqrt{2}. - Physics: This expression may appear in physical formulas where scaling of root values is necessary.
- Trigonometry: Trigonometric calculations sometimes involve such expressions in angle or distance computations.
Visual Representation
Graphically, 3 × \sqrt{2} can be visualized on a number line or as the length of the hypotenuse in a right-angled triangle where the legs are scaled by \sqrt{2}. Below is a table illustrating the step-by-step calculation:
| Step | Calculation | Result |
|---|---|---|
| 1 | Determine \sqrt{2} |
1.414 |
| 2 | Multiply by 3 | 3 × 1.414 |
| 3 | Approximate | 4.242 |
Related Calculations
Other related calculations involving the square root of 2 include:
\sqrt{2} \times \sqrt{2} = 2\sqrt{2}/2 = 0.7072\sqrt{2} = 2.828
The expression 3 × \sqrt{2} demonstrates the fundamental principles of multiplying irrational numbers and is crucial in various fields requiring precise numerical analysis.
READ MORE:
Introduction to 3 × Square Root of 2
The expression 3 × \sqrt{2} is a fascinating mathematical entity that blends the concepts of multiplication and irrational numbers. To understand it fully, we must delve into its computation, properties, and applications.
In mathematical terms, multiplying three by the square root of two can be expressed as:
\[ 3 \times \sqrt{2} \approx 3 \times 1.414 = 4.242 \]
Here's a step-by-step breakdown:
- Step 1: Identify the value of
\sqrt{2}, which is approximately 1.414. - Step 2: Multiply this value by 3.
- Step 3: The result is approximately 4.242, a crucial figure in various mathematical and physical applications.
This calculation shows how 3 \times \sqrt{2} bridges basic arithmetic with the complexities of irrational numbers.
Additionally, the expression 3 \times \sqrt{2} finds significance in multiple areas:
- Geometry: It can represent distances and diagonal measurements in geometric figures, particularly in scaling or transformations.
- Trigonometry: It appears in solving trigonometric problems where irrational multipliers are involved.
- Physics: Used in formulas where scaling factors and square roots intersect, such as in wave equations and quantum mechanics.
To visualize it, consider a right-angled triangle where the sides are scaled by \sqrt{2}. If one side is 3\sqrt{2}, the length calculation of the hypotenuse or other sides can involve this expression.
In conclusion, 3 \times \sqrt{2} is not just a numerical expression but a gateway to deeper mathematical understanding, enhancing our comprehension of both pure and applied mathematics.
Mathematical Explanation and Calculation
The expression 3 \times \sqrt{2} is a combination of a constant and an irrational number, resulting in a value that blends rational and irrational components. Here's a detailed breakdown of its calculation and properties.
To calculate 3 \times \sqrt{2}:
- Identify the Square Root: Determine the square root of 2, denoted as
\sqrt{2}. The value of\sqrt{2}is approximately 1.414. - Multiply by 3: Multiply this value by 3:
- Approximate the Product: The result of this multiplication is approximately 4.242.
\[ 3 \times \sqrt{2} \approx 3 \times 1.414 \]
This can be summarized in a step-by-step table:
| Step | Description | Value |
|---|---|---|
| 1 | Determine \sqrt{2} |
1.414 |
| 2 | Multiply by 3 | 3 \times 1.414 |
| 3 | Result | 4.242 |
This simple calculation provides a foundation for understanding how irrational numbers interact with whole numbers. Here are some additional insights:
- Irrational Nature: The result of multiplying a rational number (3) by an irrational number (
\sqrt{2}) remains irrational. - Usage in Geometry: The expression often appears in geometric contexts, such as calculating the length of the diagonal in a square with sides of length 3 units.
- Trigonometric Applications: It is used in various trigonometric calculations where scaling factors involve square roots.
Furthermore, 3 \times \sqrt{2} has interesting properties when applied to algebraic equations and physics problems. For instance, in quadratic equations, the roots may involve multiples of \sqrt{2}, leading to complex solutions that highlight the interplay between rational and irrational elements.
Understanding the computation and implications of 3 \times \sqrt{2} enriches our grasp of mathematical principles, making it a valuable expression in both theoretical and applied mathematics.
Applications in Geometry
The expression 3 \times \sqrt{2} plays a crucial role in various geometric contexts, often providing insights into lengths, areas, and relationships between different geometric figures. Here’s a detailed look at its applications:
1. Diagonal of a Square
One of the most common uses of 3 \times \sqrt{2} is in calculating the diagonal of a square. For a square with a side length of 3, the diagonal can be computed as:
\[ \text{Diagonal} = \text{side length} \times \sqrt{2} = 3 \times \sqrt{2} \]
This yields a diagonal length of approximately 4.242 units, which is critical in design and construction for determining space diagonals.
2. Scaling and Transformations
The factor \sqrt{2} is used to scale lengths in geometric transformations. When scaling a figure by 3 \times \sqrt{2}, the transformation can be described by:
- Identify the original length: For instance, a side length of
3. - Apply the scaling factor: Multiply by
\sqrt{2}to achieve the transformed length.
This scaling is essential in operations involving dilation and similarity in geometry.
3. Right-Angled Triangles
In right-angled triangles, 3 \times \sqrt{2} can represent the length of one of the legs or the hypotenuse, depending on the given sides. Consider a triangle where one leg is 3 units:
\[ \text{Hypotenuse} = \sqrt{(3^2 + (3 \times \sqrt{2})^2)} \]
\]
This computation helps in solving problems involving distances and angles within right-angled triangles.
4. Area Calculations
The expression can also be involved in area calculations for specific geometric shapes. For example, consider a rectangle where the sides are 3 \times \sqrt{2} and 3 units:
\[ \text{Area} = \text{length} \times \text{width} = (3 \times \sqrt{2}) \times 3 \approx 12.726 \, \text{square units} \]
This application is particularly useful in determining the area of scaled figures or when working with non-standard dimensions.
5. Volumes of 3D Shapes
When extending to three dimensions, 3 \times \sqrt{2} can determine one of the dimensions of a prism or cylinder, affecting the volume calculation:
\[ \text{Volume} = \text{Base Area} \times \text{height} \]
where the height might be 3 \times \sqrt{2}, showing its importance in spatial geometry.
In conclusion, 3 \times \sqrt{2} is a versatile expression in geometry, aiding in understanding and solving problems related to lengths, areas, and volumes. Its application extends beyond simple computations, providing essential insights into geometric relationships and transformations.
Significance in Algebra and Trigonometry
The expression 3 \times \sqrt{2} holds considerable significance in both algebra and trigonometry, influencing various problem-solving strategies and mathematical concepts. This section explores its impact and application in these fields.
Algebraic Significance
In algebra, 3 \times \sqrt{2} demonstrates the interaction between rational and irrational numbers, often appearing in equations and inequalities:
- Solving Equations: Consider a linear equation where
3 \times \sqrt{2}appears as a coefficient or constant term. For instance, solving forxin the equation: - Quadratic Equations: The roots of quadratic equations can involve
3 \times \sqrt{2}. For example, in the equation: - Inequalities: When solving inequalities,
3 \times \sqrt{2}might define boundary values or intervals, influencing the solution set.
\[ 5x + 3 \times \sqrt{2} = 10 \]
requires isolating x and dealing with the irrational component.
\[ x^2 - 6\sqrt{2}x + 9 = 0 \]
the term 6\sqrt{2} represents the sum of the roots scaled by 3.
Trigonometric Significance
In trigonometry, 3 \times \sqrt{2} assists in solving problems involving angles, lengths, and transformations:
- Trigonometric Identities: The expression can be used in identities and formulas. For example, in solving for hypotenuse lengths or verifying identities like:
- Angle Measures: Consider a scenario where the sides of a triangle are scaled by
3 \times \sqrt{2}. The resulting angle measures are adjusted accordingly, using trigonometric functions to calculate precise values. - Transformations: In geometric transformations involving rotation or reflection,
3 \times \sqrt{2}can serve as a scaling factor for translating figures on the coordinate plane.
\[ \sin(\theta) = \frac{3 \times \sqrt{2}}{r} \]
where r is the hypotenuse in a right-angled triangle.
Example Problems
Let’s explore an example problem involving trigonometry:
- Problem: Find the length of the side opposite an angle
\thetain a right-angled triangle where the hypotenuse is3 \times \sqrt{2}units long. - Solution: Use the sine function:
\[ \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} \] \]
Rearranging gives:
\[ \text{opposite} = 3 \times \sqrt{2} \times \sin(\theta) \]Substituting a known value of
\theta, say 45°, yields:
\[ \text{opposite} = 3 \times \sqrt{2} \times \sin(45^\circ) = 3 \times \sqrt{2} \times \frac{1}{\sqrt{2}} = 3 \]
This example highlights how 3 \times \sqrt{2} can simplify trigonometric calculations, providing precise solutions for lengths and angles in right-angled triangles.
In summary, 3 \times \sqrt{2} enhances algebraic manipulations and trigonometric problem-solving, making it a valuable expression for exploring the properties and relationships within these mathematical fields.

Visualization and Graphical Representation
Visualizing the expression 3 \times \sqrt{2} offers a deeper understanding of its geometric and algebraic properties. This section explores methods to represent this value graphically, enhancing comprehension through visual aids.
1. Number Line Representation
To represent 3 \times \sqrt{2} on a number line:
- Mark the Origin: Start by marking the point
0on the number line. - Identify
\sqrt{2}: Mark the approximate position of\sqrt{2}, around1.414. - Scale by 3: Multiply this distance by 3 to locate
3 \times \sqrt{2}. The point will be approximately4.242units from the origin.
This helps in understanding the relative magnitude of 3 \times \sqrt{2} on a linear scale.
2. Geometric Representation
Geometrically, 3 \times \sqrt{2} can be visualized in the context of shapes and transformations:
- Diagonal of a Square: Consider a square with a side length of
3units. The diagonal can be calculated as:\[ \text{Diagonal} = 3 \times \sqrt{2} \]
This diagonal extends across the square, visualizing the length
3 \times \sqrt{2}as a spatial measurement. - Rectangle Area: A rectangle with one side
3units and the other\sqrt{2}units scaled by 3 forms an area of:\[ \text{Area} = 3 \times (3 \times \sqrt{2}) = 9 \sqrt{2} \]
These visualizations illustrate how 3 \times \sqrt{2} interacts with geometric figures.
3. Graphical Plotting
Plotting 3 \times \sqrt{2} on a graph involves the following steps:
- Set Up Axes: Draw a Cartesian coordinate system with x and y axes.
- Plot
3 \times \sqrt{2}: On the x-axis, plot the point at4.242units (the approximate value of3 \times \sqrt{2}). - Visualize the Point: Mark the point clearly to show the exact value of
3 \times \sqrt{2}in the context of the graph.
This approach helps visualize the value within a coordinate system, aiding in its interpretation in algebraic contexts.
4. Dynamic Representation with Software
Using software tools like graphing calculators or computer algebra systems allows for dynamic visualizations:
- Graphing Tools: Input
3 \times \sqrt{2}into graphing tools to observe its behavior in functions and transformations. - Interactive Models: Create interactive geometric models that adjust dynamically as
3 \times \sqrt{2}is manipulated, providing a real-time visual understanding of its effects.
These tools enhance the understanding of 3 \times \sqrt{2} by providing interactive and dynamic visualizations.
In conclusion, visualizing 3 \times \sqrt{2} through number lines, geometric figures, and graphical plotting aids in comprehending its properties and applications in mathematics, making abstract concepts more tangible and accessible.
Properties of Irrational Numbers
Irrational numbers, such as \( 3 \times \sqrt{2} \), possess unique mathematical properties that distinguish them from rational numbers:
- Non-Repeatability: Unlike rational numbers which can be expressed as fractions, irrational numbers cannot be represented as a simple fraction of integers.
- Non-Terminating Decimal: The decimal representation of irrational numbers neither terminates nor repeats.
- Unlimited Precision: Irrational numbers have an infinite number of non-repeating digits in their decimal expansions, making them challenging to represent precisely.
- Transcendental Nature: Some irrational numbers are also transcendental, meaning they are not roots of any non-zero polynomial equation with rational coefficients.
- Density in the Number Line: Irrational numbers are densely packed within the real number line, meaning between any two rational numbers there exists an irrational number.
- Mathematical Constants: Many important mathematical constants, such as \( \pi \) and \( e \), are irrational, highlighting their fundamental role in mathematics.
Understanding the properties of irrational numbers is crucial in various fields of mathematics and their applications, including geometry, physics, and computer science.
Examples and Real-Life Applications
The value \( 3 \times \sqrt{2} \) appears in various real-life scenarios, demonstrating its practical significance:
- Engineering: Used in structural engineering for calculations involving diagonal measurements and load distributions.
- Physics: Relevant in calculations related to wave propagation and energy transfer, particularly in electromagnetism and optics.
- Computer Graphics: Utilized in algorithms for image processing and 3D modeling, determining dimensions and scaling factors.
- Finance: Applied in financial models for risk assessment and investment analysis, involving growth rates and inflation adjustments.
- Education: Used in educational contexts to illustrate concepts of irrational numbers and their applications across different disciplines.
Comparison with Other Multiples of Square Roots
Comparing \( 3 \times \sqrt{2} \) with other multiples of square roots reveals interesting contrasts and applications:
| Expression | Properties | Applications |
| \( 2 \times \sqrt{3} \) | Another irrational number involving a different square root, with non-terminating decimal. | Used in geometry for calculations involving areas of regular polygons. |
| \( 5 \times \sqrt{2} \) | A multiple of \( \sqrt{2} \) with a different coefficient, showcasing varied scaling properties. | Common in physics for wave phenomena and signal processing. |
| \( 4 \times \sqrt{5} \) | Involves a larger multiple and a different square root, influencing more complex calculations. | Found in engineering for structural analysis and load-bearing calculations. |
Each expression represents a unique combination of a rational coefficient and an irrational square root, each with specific mathematical properties and practical applications in different fields.

Related Mathematical Concepts
Exploring \( 3 \times \sqrt{2} \) leads to connections with various mathematical concepts:
- Irrational Numbers: Understanding the nature of irrational numbers and their properties.
- Pythagorean Theorem: Application in geometric proofs involving right triangles.
- Trigonometric Functions: Relationships with sine, cosine, and tangent functions in right triangle calculations.
- Algebraic Manipulation: Techniques for simplifying expressions involving radicals and rationalizing denominators.
- Geometric Mean: Use in calculating averages and proportional relationships in geometry and statistics.
Conclusion and Summary
In conclusion, \( 3 \times \sqrt{2} \) exemplifies the beauty and complexity of irrational numbers in mathematics:
- Mathematical Significance: It represents a precise value that is both non-repeating and non-terminating.
- Practical Applications: From engineering to physics, its utility spans various disciplines, showcasing its versatility.
- Educational Value: Studying this expression enriches understanding of irrational numbers and their role in mathematical theories.
- Interdisciplinary Connections: It links to concepts in geometry, algebra, trigonometry, and beyond, illustrating its interconnectedness in mathematics.
- Continued Exploration: Further research into similar mathematical expressions fosters deeper insights into the fundamental principles of mathematics.
Overall, \( 3 \times \sqrt{2} \) serves as a prime example of how mathematical concepts transcend theoretical boundaries to impact real-world applications and intellectual inquiry.
Khám phá cách giải phương trình 1/3 nhân căn bậc hai của 2x = 2 và hiểu sâu hơn về nó. Nhiều người vẫn chưa hiểu đầy đủ điều này!
1/3 Nhân Căn Bậc Hai của 2x = 2, Nhiều Người Không Hiểu Đầy Đủ Điều Này!
READ MORE:
Tìm Nghiệm Của Phương Trình Bậc Hai 3x² - 2√6x + 2 = 0