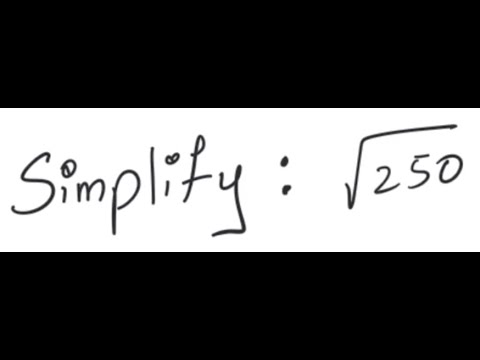Square Root of 2x: Simplifying, Graphing, and Solving Equations

The mathematical concept of the square root of 2x can be explored through various algebraic techniques and graphical representations. Below are some detailed steps and explanations:

Simplifying the Square Root of 2x

To simplify the expression $$

2x

, we can follow these steps:

1. Identify the radicand (the expression under the square root). In this case, it is 2x.
2. Check if the radicand can be simplified further. Here, 2 and x are already in their simplest forms.
3. Since nothing further can be done to simplify $\sqrt{2x}$, the expression remains as it is.

For example, the expression $$

2x(
2
-
x
)

can be simplified by applying the distributive property and combining like terms using the product rule for radicals.

Graphing the Square Root of 2x

To graph the function $$
y=
2x

, follow these steps:

1. Determine the domain of the function. The radicand must be greater than or equal to zero: $2x\ge 0$. Therefore, $x\ge 0$.
2. Find the key points by substituting values of x within the domain into the function. For example, when $x=0$, $y=\sqrt{2\left(0\right)}=0$. When $x=1$, $y=\sqrt{2\left(1\right)}=\sqrt{2}$.
3. Plot these points on a coordinate plane and draw a smooth curve passing through them to represent the function.

The graph of $$
y=
2x

starts at the origin (0,0) and increases gradually, reflecting the nature of the square root function.

Example Problem

Consider the problem of simplifying the expression $$

2x(
2
-
x
)

:

1. Apply the distributive property: $\sqrt{2x}\sqrt{2}-\sqrt{2x\sqrt{x}}$.
2. Simplify using the product rule for radicals: $2-\sqrt{2x\bullet x}$.
3. The simplified expression is: $2-\sqrt{2x^2}$.

Additional Resources

The square root of \(2x\) is a vital concept in algebra and calculus, forming the foundation for various mathematical applications. In this section, we will delve into the core aspects of the square root of \(2x\), helping you build a solid understanding.

• Definition: The square root function is represented as \(\sqrt{2x}\), where \(2x\) is the radicand.
• Importance: Understanding the square root of \(2x\) is crucial for simplifying expressions, solving equations, and graphing functions.
• Applications: This concept is used in diverse fields such as physics, engineering, and computer science.

Here are the key points we'll cover:

1. Simplifying: Learn techniques to simplify expressions involving \(\sqrt{2x}\).
2. Graphing: Understand how to plot the graph of \(y = \sqrt{2x}\) and interpret its features.
3. Solving Equations: Master methods to solve equations that include the square root of \(2x\).
4. Applications: Explore practical examples and real-world applications of \(\sqrt{2x}\).

By the end of this article, you will have a comprehensive grasp of the square root of \(2x\) and be equipped with the skills to apply this knowledge effectively.

The concept of square roots is fundamental in mathematics, providing a foundation for more complex topics. The square root of a number \(x\) is a value that, when multiplied by itself, gives \(x\). Mathematically, the square root of \(x\) is denoted as \(\sqrt{x}\).

• Basic Definition: For any non-negative number \(x\), the square root of \(x\) is a number \(y\) such that \(y^2 = x\).
• Principal Square Root: The principal square root is the non-negative root and is denoted by \(\sqrt{x}\). For example, \(\sqrt{9} = 3\).
• Negative Roots: Every positive number \(x\) has two square roots: \(\sqrt{x}\) and \(-\sqrt{x}\). However, by convention, \(\sqrt{x}\) refers to the principal (non-negative) square root.

Square roots play a crucial role in various mathematical operations and problem-solving scenarios. Here are the key properties and rules:

1. Product Rule: \(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\). For example, \(\sqrt{4 \cdot 9} = \sqrt{4} \cdot \sqrt{9} = 2 \cdot 3 = 6\).
2. Quotient Rule: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\). For instance, \(\sqrt{\frac{16}{4}} = \frac{\sqrt{16}}{\sqrt{4}} = \frac{4}{2} = 2\).
3. Power Rule: \((\sqrt{a})^2 = a\). For example, \((\sqrt{5})^2 = 5\).

Understanding these basic principles allows us to explore more complex functions involving square roots, such as the square root of \(2x\). By mastering the foundational rules, you will be better prepared to simplify, solve, and graph expressions involving square roots.

Solving equations involving the square root of \(2x\) requires isolating the square root and then squaring both sides of the equation to eliminate it. This method transforms the equation into a more manageable form. Let's explore the steps with detailed examples.

Follow these steps to solve equations involving \(\sqrt{2x}\):

1. Isolate the Square Root: Rearrange the equation so that the square root term is by itself on one side of the equation.
2. Square Both Sides: Square both sides of the equation to eliminate the square root. This step will result in a quadratic equation or a linear equation.
3. Solve the Resulting Equation: Solve the quadratic or linear equation obtained from squaring both sides.
4. Check for Extraneous Solutions: Substituting the solutions back into the original equation is necessary to ensure they are valid, as squaring both sides can introduce extraneous solutions.

Let's work through some examples:

• Example 1: Solve \(\sqrt{2x} = 4\)
  1. Isolate the square root: The square root is already isolated.
  2. Square both sides: \((\sqrt{2x})^2 = 4^2\)
  3. Simplify: \(2x = 16\)
  4. Solve for \(x\): \(x = \frac{16}{2} = 8\)
  5. Check the solution: \(\sqrt{2 \cdot 8} = \sqrt{16} = 4\) (valid solution)
• Example 2: Solve \(\sqrt{2x + 3} = x\)
  1. Isolate the square root: The square root is already isolated.
  2. Square both sides: \((\sqrt{2x + 3})^2 = x^2\)
  3. Simplify: \(2x + 3 = x^2\)
  4. Rearrange into standard form: \(x^2 - 2x - 3 = 0\)
  5. Factor the quadratic: \((x - 3)(x + 1) = 0\)
  6. Solve for \(x\): \(x = 3\) or \(x = -1\)
  7. Check the solutions:
     • For \(x = 3\): \(\sqrt{2 \cdot 3 + 3} = \sqrt{9} = 3\) (valid)
     • For \(x = -1\): \(\sqrt{2 \cdot -1 + 3} = \sqrt{1} = 1 \neq -1\) (not valid)

By following these steps, you can effectively solve equations involving the square root of \(2x\). Remember to always check for extraneous solutions to ensure the validity of your answers.

The square root of \(2x\) has various practical applications in different fields, such as physics, engineering, and everyday problem-solving. Understanding how to apply this concept can enhance your ability to tackle real-world challenges.

Here are some practical examples and applications:

• Physics:

  In physics, the square root of \(2x\) can be used in kinematic equations, especially when dealing with uniform acceleration. For instance, the formula for the velocity \(v\) of an object under uniform acceleration \(a\) is given by \(v = \sqrt{2ax}\), where \(x\) is the displacement.

• Engineering:

  Engineers often use the square root of \(2x\) when dealing with stress and strain calculations. For example, in structural engineering, the stress on a beam can be related to the square root of its deflection, where \(x\) represents the load applied to the beam.

• Economics:

  In economics, the square root of \(2x\) can be applied in cost-benefit analysis. For example, the cost function \(C(x)\) might involve square roots to model diminishing returns, where \(x\) represents the quantity of goods produced.

• Everyday Problem-Solving:

  The square root of \(2x\) can also be useful in everyday situations. For example, if you are planning to build a rectangular garden and you know the area \(A\), you can use the square root to find the dimensions of the garden. If the length is twice the width, then \(A = 2x \cdot x = 2x^2\), and the width \(x\) can be found using \(x = \sqrt{\frac{A}{2}}\).

Let's look at some detailed examples:

1. Example 1: Kinematics

   An object is accelerating uniformly at \(4 \, \text{m/s}^2\). Find its velocity after it has traveled \(16 \, \text{meters}\).

   1. Given \(a = 4 \, \text{m/s}^2\) and \(x = 16 \, \text{m}\), use \(v = \sqrt{2ax}\).
   2. Substitute the values: \(v = \sqrt{2 \cdot 4 \cdot 16} = \sqrt{128} = 8\sqrt{2} \, \text{m/s}\).
2. Example 2: Structural Engineering

   A beam experiences a deflection \(\delta\) under a load \(P\). The relationship is given by \(\delta = \sqrt{2Px}\), where \(x\) is a constant depending on the beam's material and dimensions. Find the deflection for \(P = 10 \, \text{kN}\) and \(x = 5 \, \text{m}\).

   1. Given \(P = 10 \, \text{kN}\) and \(x = 5 \, \text{m}\), use \(\delta = \sqrt{2Px}\).
   2. Substitute the values: \(\delta = \sqrt{2 \cdot 10 \cdot 5} = \sqrt{100} = 10 \, \text{mm}\).

These examples illustrate how the square root of \(2x\) is not just a mathematical abstraction but a tool with practical utility in various fields.

The square root of \(2x\) is a versatile mathematical function with a wide range of applications in various fields such as physics, engineering, and everyday problem-solving. Understanding how to simplify, graph, and solve equations involving \(\sqrt{2x}\) is essential for both theoretical and practical purposes.

In this article, we have explored several key aspects:

• Understanding Square Roots: We discussed the fundamental concept of square roots, their properties, and rules for simplification.
• Simplifying the Square Root of 2x: We provided step-by-step methods for simplifying expressions involving \(\sqrt{2x}\), along with illustrative examples.
• Graphing the Square Root of 2x: We detailed the process of graphing \(y = \sqrt{2x}\), highlighting important points and the shape of the graph.
• Solving Equations Involving the Square Root of 2x: We covered the steps to solve equations with \(\sqrt{2x}\), emphasizing the importance of checking for extraneous solutions.
• Practical Examples and Applications: We demonstrated the practical utility of \(\sqrt{2x}\) through real-world examples in physics, engineering, and everyday life.

By mastering these concepts, you are better equipped to handle mathematical problems and apply the square root of \(2x\) in various contexts. The ability to work with square roots is a valuable skill that enhances your problem-solving toolkit and deepens your understanding of mathematical principles.

Continue practicing and exploring further applications of \(\sqrt{2x}\) to strengthen your proficiency and confidence in using this important mathematical function.