Topic square root of 500 in radical form: The square root of 500 in radical form is a fascinating topic that combines simplicity with depth. This article will guide you through the steps to simplify the square root of 500, providing clear explanations and practical examples. Discover how understanding radical expressions can be both enlightening and useful in various mathematical contexts.
Table of Content
- Square Root of 500 in Radical Form
- Introduction to Square Roots
- Understanding Radicals
- Definition and Properties of Square Roots
- Steps to Simplify the Square Root of 500
- Breaking Down 500 into Prime Factors
- Combining Like Terms in Radical Form
- Simplifying Square Root of 500
- Expressing Square Root of 500 in Simplified Radical Form
- Comparing Exact Form vs Decimal Form
- Applications of Simplified Radicals
- Common Mistakes to Avoid
- Practice Problems
- Conclusion and Key Takeaways
- YOUTUBE: Video này hướng dẫn cách tính căn bậc hai của 500 và giải thích cách đơn giản hóa biểu thức trong dạng căn.
Square Root of 500 in Radical Form
The square root of 500 can be expressed in radical form as follows:
Prime Factorization Method
To find the square root of 500 using the prime factorization method, we start by finding the prime factors of 500:
- Prime factors of 500: \(2^2 \times 5^3\)
- Grouping the prime factors in pairs: \((2 \times 2) \times (5 \times 5) \times 5\)
- Taking the square root of each pair: \(\sqrt{500} = \sqrt{(2 \times 2) \times (5 \times 5) \times 5}\)
- Extracting pairs from the radical: \(\sqrt{500} = 2 \times 5 \times \sqrt{5}\)
- Simplifying: \(\sqrt{500} = 10\sqrt{5}\)
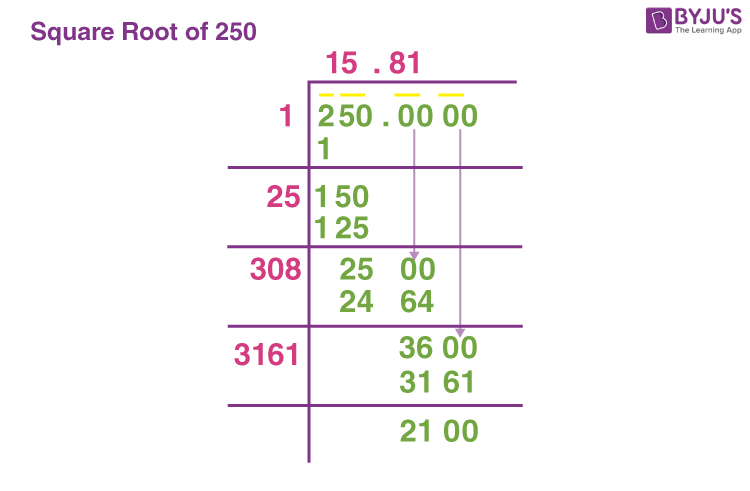
Long Division Method
Another method to find the square root of 500 is the long division method. Here are the steps:
- Pair the digits of 500 from right to left: 500.000000
- Find the largest number whose square is less than or equal to 5: \(2 \times 2 = 4\)
- Subtract and bring down the next pair of digits: \(5 - 4 = 1\), bringing down 00 gives 100
- Double the quotient and use it as the next divisor: \(2 \times 2 = 4\), so the new divisor is 40
- Find the number that fits: \(40 \times 2 = 80\), so the quotient becomes 22 and the remainder is 20
- Continue the process to get more decimal places
The approximate value of \(\sqrt{500}\) is 22.3607.
Examples
Here are some examples demonstrating the use of the square root of 500 in calculations:
- Simplifying \(4\sqrt{500}\):
- Finding the smallest multiple of 500 which is a perfect square:
Given \(4\sqrt{500}\), we know \(\sqrt{500} = 22.3607\). So, \(4\sqrt{500} = 4 \times 22.3607 = 89.4428\).
The prime factorization of 500 is \(2^2 \times 5^3\). To make it a perfect square, we need each exponent to be even. Thus, the smallest multiple is \(500 \times 5 = 2500\), and the square root of 2500 is 50.
FAQs
- What is the value of the square root of 500?
- Why is the square root of 500 an irrational number?
- What is the square root of 500 in simplest radical form?
The square root of 500 is approximately 22.3607.
Because the prime factorization of 500 contains an odd power of 5, making it irrational.
The simplest radical form of the square root of 500 is \(10\sqrt{5}\).

READ MORE:
Introduction to Square Roots
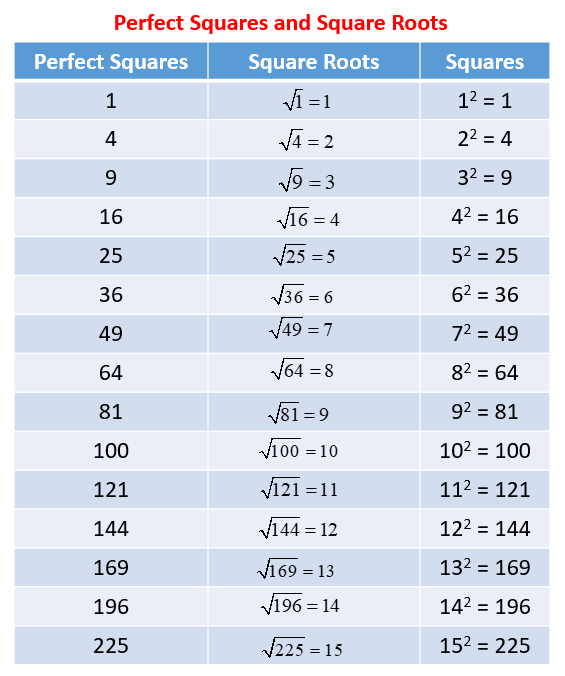
Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5, because \(5 \times 5 = 25\). In this section, we will explore the basics of square roots and how to simplify them.
To understand square roots, consider the following points:
- Definition: The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \).
- Notation: The square root of \( x \) is denoted as \( \sqrt{x} \).
- Properties:
- For any positive number \( x \), \( \sqrt{x} \) is always positive.
- \( \sqrt{x^2} = x \) for any non-negative \( x \).
- The square root of a product is the product of the square roots: \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \).
Square roots can be simplified by identifying and factoring out perfect squares. Let's look at an example to illustrate this:
| Example: | Finding the square root of 36. |
| Step 1: | Identify the perfect square factor of 36. Here, \(36 = 6 \times 6\). |
| Step 2: | Take the square root of the perfect square. So, \( \sqrt{36} = \sqrt{6 \times 6} = 6\). |
Now, let's consider a non-perfect square example:
| Example: | Finding the square root of 50. |
| Step 1: | Factor 50 into its prime factors: \(50 = 2 \times 5 \times 5\). |
| Step 2: | Group the factors into pairs of squares: \(50 = 5^2 \times 2\). |
| Step 3: | Take the square root of each pair: \( \sqrt{50} = \sqrt{5^2 \times 2} = 5 \sqrt{2} \). |
In summary, understanding square roots involves recognizing and simplifying radical expressions, factoring numbers into their prime components, and applying the properties of square roots. This foundational knowledge is crucial for simplifying more complex radicals, such as the square root of 500, which we will explore further in this article.
Understanding Radicals
Radicals are mathematical expressions that involve roots, such as square roots, cube roots, and higher-order roots. The most common radical is the square root, which is denoted by the symbol \( \sqrt{} \). In this section, we will delve into the basics of radicals, their properties, and how to work with them effectively.
Key concepts of radicals include:
- Definition: A radical expression is an expression that includes a root symbol. For example, \( \sqrt{a} \) is the square root of \( a \).
- Radicand: The number or expression inside the root symbol is called the radicand. In \( \sqrt{a} \), \( a \) is the radicand.
- Index: The index of a radical indicates the degree of the root. For square roots, the index is 2 and is usually omitted. For cube roots, the index is 3 and is written as \( \sqrt[3]{a} \).
Properties of radicals are essential for simplifying and manipulating radical expressions:
- Product Property: The square root of a product is the product of the square roots: \[ \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \]
- Quotient Property: The square root of a quotient is the quotient of the square roots: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \]
- Power Property: The nth root of a number raised to the nth power is the number itself: \[ \sqrt[n]{a^n} = a \]
Let's apply these properties to an example involving the square root of 500:
| Example: | Simplifying the square root of 500. |
| Step 1: | Factor 500 into its prime factors: \(500 = 2^2 \times 5^3\). |
| Step 2: | Apply the product property: \(\sqrt{500} = \sqrt{2^2 \times 5^3}\). |
| Step 3: | Simplify by taking the square root of the perfect squares: \[ \sqrt{2^2 \times 5^3} = \sqrt{2^2} \times \sqrt{5^2 \times 5} = 2 \times 5 \sqrt{5} = 10\sqrt{5} \] |
In summary, understanding radicals involves recognizing their components, properties, and methods for simplification. By mastering these concepts, you can confidently work with various radical expressions, such as simplifying the square root of 500 to \(10\sqrt{5}\).
Definition and Properties of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the radical symbol \( \sqrt{} \). For example, the square root of 25 is 5 because \( 5 \times 5 = 25 \). Square roots are fundamental in mathematics and have several important properties.
Here are the key properties of square roots:
- Non-negativity: The square root of a non-negative number is also non-negative. For any \( x \geq 0 \), \( \sqrt{x} \geq 0 \).
- Product Property: The square root of a product is the product of the square roots: \[ \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \] for any non-negative numbers \( a \) and \( b \).
- Quotient Property: The square root of a quotient is the quotient of the square roots: \[ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \] for any non-negative numbers \( a \) and \( b \), where \( b \neq 0 \).
- Power Property: The square root of a number raised to the power of 2 is the number itself: \[ \sqrt{x^2} = x \] for any non-negative number \( x \).
- Square of a Square Root: The square of a square root returns the original number: \[ (\sqrt{x})^2 = x \] for any non-negative number \( x \).
Let's illustrate these properties with examples:
| Example 1: | Product Property |
| Given: | \(\sqrt{9 \times 4}\) |
| Solution: | \[ \sqrt{9 \times 4} = \sqrt{36} = 6 \] Using the product property: \[ \sqrt{9} \times \sqrt{4} = 3 \times 2 = 6 \] |
| Example 2: | Quotient Property |
| Given: | \(\sqrt{\frac{16}{4}}\) |
| Solution: | \[ \sqrt{\frac{16}{4}} = \sqrt{4} = 2 \] Using the quotient property: \[ \frac{\sqrt{16}}{\sqrt{4}} = \frac{4}{2} = 2 \] |
Understanding the definition and properties of square roots is crucial for simplifying and working with radical expressions. These properties are especially useful when dealing with more complex numbers, such as simplifying the square root of 500.
Steps to Simplify the Square Root of 500
To simplify the square root of 500, follow these detailed steps:
-
Prime Factorization: Break down 500 into its prime factors. The prime factorization of 500 is:
\[
500 = 2^2 \times 5^3
\] -
Group the Factors: Group the prime factors into pairs of two:
\[
500 = (2^2) \times (5^2) \times 5
\] -
Simplify the Square Root: Take the square root of each pair of prime factors and move them outside the radical:
\[
\sqrt{500} = \sqrt{(2^2) \times (5^2) \times 5} = 2 \times 5 \times \sqrt{5} = 10\sqrt{5}
\]
Thus, the square root of 500 in its simplest radical form is:
\[
10\sqrt{5}
\]

Breaking Down 500 into Prime Factors
To simplify the square root of 500, we first need to break down 500 into its prime factors. Here are the steps:
Identify the prime numbers that multiply together to give the original number, 500. Start by dividing 500 by the smallest prime number, which is 2:
\( 500 \div 2 = 250 \)
Next, continue dividing by 2 until it is no longer divisible by 2:
\( 250 \div 2 = 125 \)
Since 125 is not divisible by 2, move to the next smallest prime number, which is 5:
\( 125 \div 5 = 25 \)
Continue dividing by 5:
\( 25 \div 5 = 5 \)
\( 5 \div 5 = 1 \)
We have now expressed 500 as a product of prime factors:
\( 500 = 2 \times 2 \times 5 \times 5 \times 5 \)
Or, in exponential form:
\( 500 = 2^2 \times 5^3 \)
Next, we will use these prime factors to simplify the square root of 500 in the next section.
Combining Like Terms in Radical Form
When simplifying the square root of a number, combining like terms in radical form is an essential step. Here are the detailed steps to combine like terms for the square root of 500:
-
Prime Factorization: Begin with the prime factorization of 500. We have:
500 = 2 × 2 × 5 × 5 × 5
-
Pairing the Factors: Group the factors into pairs of equal numbers where possible:
(2 × 2) × (5 × 5) × 5
-
Taking Square Roots: Take the square root of each pair of factors. This step involves moving the square root of a product to the product of the square roots:
√(2 × 2) × √(5 × 5) × √5
Since √(2 × 2) = 2 and √(5 × 5) = 5, we get:
2 × 5 × √5
-
Combining the Results: Multiply the numbers outside the radical and keep the remaining factor inside the radical:
10 × √5
Thus, the simplified radical form of the square root of 500 is:
\[\sqrt{500} = 10\sqrt{5}\]
This process involves identifying and pairing the prime factors, taking the square root of each pair, and then combining the results to express the original number in its simplest radical form.
Simplifying Square Root of 500
To simplify the square root of 500, we need to break it down into its prime factors and then simplify the radical expression. Follow these steps:
- Start with the number 500.
- Find the prime factorization of 500.
The prime factorization of 500 is:
\[ 500 = 2^2 \times 5^3 \]
- Express the square root of 500 using its prime factors.
\[ \sqrt{500} = \sqrt{2^2 \times 5^3} \]
- Separate the factors under the radical into pairs, where possible.
\[ \sqrt{500} = \sqrt{2^2} \times \sqrt{5^2 \times 5} \]
- Simplify the square root of each pair of prime factors.
\[ \sqrt{2^2} = 2 \]
\[ \sqrt{5^2} = 5 \]
- Combine the simplified factors outside the radical with the remaining factor inside the radical.
\[ \sqrt{500} = 2 \times 5 \times \sqrt{5} \]
- Multiply the numbers outside the radical.
\[ \sqrt{500} = 10\sqrt{5} \]
Therefore, the simplified radical form of \(\sqrt{500}\) is:
\[ \boxed{10\sqrt{5}} \]
Expressing Square Root of 500 in Simplified Radical Form
To express the square root of 500 in its simplified radical form, follow these steps:
-
Prime Factorization: Start by finding the prime factors of 500. The prime factorization of 500 is:
\[ 500 = 2^2 \times 5^3 \]
-
Grouping Factors: Next, group the factors into pairs:
\[ 500 = (2 \times 2) \times (5 \times 5) \times 5 \]
-
Simplifying the Square Root: Take the square root of each pair of factors:
\[ \sqrt{500} = \sqrt{(2 \times 2) \times (5 \times 5) \times 5} = \sqrt{2^2 \times 5^2 \times 5} \]
\[ \sqrt{500} = 2 \times 5 \times \sqrt{5} = 10\sqrt{5} \]
Therefore, the simplified radical form of the square root of 500 is:
\[ \sqrt{500} = 10\sqrt{5} \]
This form is more compact and often preferred in mathematical expressions as it shows the simplest form of the radical.

Comparing Exact Form vs Decimal Form
When dealing with square roots, we often compare the exact form (radical form) with the decimal form to understand the precision and practical usage. Here, we will look at the square root of 500 in both forms.
The square root of 500 in its exact form is expressed as:
\[
\sqrt{500} = \sqrt{4 \times 125} = \sqrt{4} \times \sqrt{125} = 2\sqrt{125}
\]
\]
This further simplifies to:
\[
2\sqrt{125} = 2 \times \sqrt{5 \times 25} = 2 \times \sqrt{5} \times \sqrt{25} = 2 \times 5\sqrt{5} = 10\sqrt{5}
\]
Therefore, the exact form of the square root of 500 is:
\[
10\sqrt{5}
\]
In decimal form, we calculate \(\sqrt{500}\) using a calculator to get an approximate value:
\[
\sqrt{500} \approx 22.360679775
\]
Comparison
- Exact Form: \(10\sqrt{5}\)
- Decimal Form: 22.360679775
The exact form, \(10\sqrt{5}\), retains the radical and is precise. It is preferred in mathematical proofs and scenarios where precision is crucial. The decimal form, 22.360679775, provides an approximation that is more practical for everyday use where an exact value is not necessary.
Below is a comparison of the two forms:
| Form | Representation | Use Case |
|---|---|---|
| Exact Form | \(10\sqrt{5}\) | Used in mathematical proofs, algebraic manipulation, and theoretical calculations where precision is essential. |
| Decimal Form | 22.360679775 | Used in practical applications, measurements, and when an approximate value suffices. |
In conclusion, both forms have their importance depending on the context. The exact form provides complete accuracy, while the decimal form offers a practical approximation.
Applications of Simplified Radicals
Simplified radicals, such as the square root of 500 expressed as \(10\sqrt{5}\), are not just theoretical constructs but have practical applications across various fields. Here are some key areas where simplified radicals are commonly used:
-
Geometry and Design:
In geometry, radicals are often used to calculate distances and dimensions. For instance, the diagonal length of a rectangle with sides of length \(a\) and \(b\) is given by \(\sqrt{a^2 + b^2}\). When designing spaces or objects, simplified radicals can help in determining precise measurements. For example, if a design requires a diagonal of 22 units approximately, knowing that \(\sqrt{500} = 10\sqrt{5} \approx 22.36\) can be very useful.
-
Physics and Engineering:
In physics, the kinetic energy (\(E_k\)) of an object is given by the formula \(E_k = \frac{1}{2}mv^2\). Sometimes, solving for velocity or other variables involves working with radicals. For example, if a specific energy calculation simplifies to an expression involving \(\sqrt{500}\), knowing the radical form as \(10\sqrt{5}\) allows for easier manipulation and understanding of the equations.
-
Algebra and Calculus:
Radicals frequently appear in algebraic equations and calculus. Simplifying expressions can make solving equations more straightforward. For example, if an integral or derivative includes \(\sqrt{500}\), using \(10\sqrt{5}\) simplifies the process and helps in finding solutions more efficiently.
-
Technology and Computer Science:
In computer algorithms, especially those involving geometric computations or optimizations, radicals are used to maintain precision. Simplifying radicals can improve the efficiency of these algorithms, reducing computational complexity.
-
Everyday Calculations:
In everyday life, whether in construction, navigation, or even finance, simplified radicals can assist in making quick and accurate calculations. For instance, understanding that \(\sqrt{500} = 10\sqrt{5}\) allows for quick mental math when estimating distances or sizes.
Overall, the ability to simplify and work with radicals such as \(10\sqrt{5}\) enhances numerical literacy and problem-solving skills, demonstrating their value beyond the classroom in practical, real-world applications.
Common Mistakes to Avoid
When simplifying the square root of 500 or dealing with radical expressions in general, there are several common pitfalls that learners and practitioners alike should be mindful of. Avoiding these mistakes ensures accurate and efficient mathematical problem-solving. Here are some key errors to watch out for:
- Overlooking Prime Factorization: Skipping the step of prime factorization can lead to incorrect simplification. Always break down the number into its prime factors to simplify accurately.
- Misapplying Radical Rules: Confusing the rules for adding, subtracting, multiplying, and dividing radicals can result in errors. Remember that you can only combine radicals with the same index and radicand.
- Ignoring the Exact Value: Relying too heavily on decimal approximations without considering the exact radical form can lead to precision loss in solutions, especially in algebra and geometry.
- Forgetting to Simplify Completely: Partial simplification of a radical expression can leave an answer that, while correct, is not in its simplest form. Ensure every pair of prime factors is accounted for.
- Incorrect Decimal Conversion: When converting a radical to its decimal form, using an inaccurate value for the square root can drastically affect the outcome. Use a calculator for precision.
Avoiding these common mistakes when working with the square root of 500 and other radical expressions not only enhances accuracy but also builds a stronger foundation in mathematical comprehension and application.
Practice Problems
Mastering the concept of simplifying square roots, such as the square root of 500, requires practice. Here are some practice problems with solutions to help reinforce your understanding of how to simplify radical expressions:
- Problem 1: Simplify the square root of 72.
- Solution:
\[
\sqrt{72} = \sqrt{2^3 \times 3^2} = 3 \times \sqrt{8} = 6\sqrt{2}
\]
- Problem 2: Simplify the square root of 128.
- Solution:
\[
\sqrt{128} = \sqrt{2^7} = 2^3 \times \sqrt{2} = 8\sqrt{2}
\]
- Problem 3: Simplify the square root of 245.
- Solution:
\[
\sqrt{245} = \sqrt{5 \times 7^2} = 7\sqrt{5}
\]
- Problem 4: Simplify the square root of 18.
- Solution:
\[
\sqrt{18} = \sqrt{2 \times 3^2} = 3\sqrt{2}
\]
- Problem 5: Simplify the square root of 450.
- Solution:
\[
\sqrt{450} = \sqrt{2 \times 3^2 \times 5^2} = 3 \times 5 \times \sqrt{2} = 15\sqrt{2}
\]
These problems illustrate the process of simplifying square roots through prime factorization and the manipulation of radical expressions. Practicing these and similar problems will enhance your ability to work with radicals efficiently.
Conclusion and Key Takeaways
Understanding the square root of 500 in its simplified radical form provides valuable insights into the nature of irrational numbers and the process of simplifying square roots. Here are the key takeaways:
- The square root of 500 is expressed in its simplest radical form as \( \sqrt{500} = 10\sqrt{5} \). This is achieved through the prime factorization method, where 500 is broken down into \( 2^2 \times 5^3 \), and simplified by combining like terms.
- The square root of 500 is an irrational number because it cannot be expressed as a simple fraction. It has a non-repeating, non-terminating decimal expansion, approximately equal to 22.3607.
- Expressing the square root of 500 in radical form is useful in various mathematical applications, such as geometry, algebra, and trigonometry, where exact values are often preferred over decimal approximations.
- Understanding the process of simplifying radicals helps in solving more complex mathematical problems and enhances overall problem-solving skills.
- Common mistakes to avoid include incorrectly combining terms under the radical sign and not fully simplifying the expression to its lowest terms.
By mastering the simplification of square roots, particularly with numbers like 500, students and math enthusiasts can build a solid foundation for more advanced mathematical concepts and applications.
Video này hướng dẫn cách tính căn bậc hai của 500 và giải thích cách đơn giản hóa biểu thức trong dạng căn.
Căn Bậc Hai Của 500
READ MORE:
Video này hướng dẫn cách đơn giản hóa căn bậc hai của 500 và cung cấp các bước chi tiết để thực hiện.
Đơn Giản Hóa Căn Bậc Hai của 500 || Căn 500