Topic 6/ square root of 2: Explore the simplification of the expression "6/ square root of 2" and its applications in various mathematical contexts. This article covers step-by-step methods to simplify the fraction, convert it into different forms, and understand its relevance in algebra and beyond.
Table of Content
- Simplifying 6 Divided by the Square Root of 2
- Understanding the Division of 6 by the Square Root of 2
- Step-by-Step Simplification Process
- Exact and Decimal Forms of the Result
- Applications in Mathematics
- Common Mistakes and Misconceptions
- Use of Square Root Calculators
- Square Root in Different Mathematical Problems
- Learning Resources and Tools
- Conclusion and Further Reading
- YOUTUBE:
Simplifying 6 Divided by the Square Root of 2
When you simplify the expression \( \frac{6}{\sqrt{2}} \), you follow these steps:
Steps to Simplify
- Multiply the numerator and the denominator by \( \sqrt{2} \) to rationalize the denominator.
- Simplify the expression.
Detailed Calculation
The expression \( \frac{6}{\sqrt{2}} \) is simplified as follows:
- Multiply both the numerator and the denominator by \( \sqrt{2} \): \[ \frac{6}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{6\sqrt{2}}{2} \]
- Simplify the fraction: \[ \frac{6\sqrt{2}}{2} = 3\sqrt{2} \]
Result
So, the simplified form of \( \frac{6}{\sqrt{2}} \) is:
\[
3\sqrt{2}
\]
Additional Information
The result can be shown in both exact and decimal forms:
- Exact Form: \( 3\sqrt{2} \)
- Decimal Form: \( 3\sqrt{2} \approx 4.2426 \)
Using Online Calculators
There are several online calculators available to simplify expressions like this:
READ MORE:
Understanding the Division of 6 by the Square Root of 2
The division of 6 by the square root of 2 can be simplified using rationalization techniques in mathematics. Rationalizing involves eliminating the square root from the denominator by multiplying both the numerator and the denominator by the square root of 2.
Start with the expression:
\( \frac{6}{\sqrt{2}} \)Multiply both the numerator and the denominator by \( \sqrt{2} \):
\( \frac{6 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} \)Simplify the denominator since \( \sqrt{2} \times \sqrt{2} = 2 \):
\( \frac{6\sqrt{2}}{2} \)Divide the numerator by the denominator:
\( 3\sqrt{2} \)
So, the simplified form of \( \frac{6}{\sqrt{2}} \) is \( 3\sqrt{2} \).
| Step | Expression |
|---|---|
| Original | \( \frac{6}{\sqrt{2}} \) |
| Multiply numerator and denominator by \( \sqrt{2} \) | \( \frac{6 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}} \) |
| Simplify | \( \frac{6\sqrt{2}}{2} \) |
| Final Result | \( 3\sqrt{2} \) |
This method helps to simplify the expression and makes it easier to work with in further calculations.
Step-by-Step Simplification Process
To simplify the division of 6 by the square root of 2, we follow a structured process involving basic algebraic rules and properties of square roots. Here is a detailed, step-by-step method:
Initial Expression: Begin with the given expression:
\[\frac{6}{\sqrt{2}}\]
Rationalize the Denominator: To eliminate the square root in the denominator, multiply both the numerator and the denominator by \(\sqrt{2}\):
\[\frac{6}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{6\sqrt{2}}{2}\]
Simplify the Fraction: Divide the numerator by the denominator:
\[\frac{6\sqrt{2}}{2} = 3\sqrt{2}\]
Result: The simplified form of the expression is:
\[3\sqrt{2}\]
This process ensures that the denominator is rationalized and the expression is in its simplest form.
Exact and Decimal Forms of the Result
When dividing 6 by the square root of 2, the result can be expressed in both exact and decimal forms. Below is the step-by-step explanation:
- Exact Form:
- Start with the expression: \( \frac{6}{\sqrt{2}} \)
- Multiply the numerator and the denominator by \( \sqrt{2} \) to rationalize the denominator: \[ \frac{6 \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} = \frac{6\sqrt{2}}{2} \]
- Simplify the fraction: \[ \frac{6\sqrt{2}}{2} = 3\sqrt{2} \]
- Thus, the exact form is \( 3\sqrt{2} \).
- Decimal Form:
- First, find the approximate value of \( \sqrt{2} \approx 1.414 \).
- Substitute this value back into the simplified expression: \[ 3 \cdot 1.414 = 4.242 \]
- Thus, the decimal form is approximately 4.242.
These forms provide both the precise and the approximate values, allowing for flexibility in various mathematical contexts.
Applications in Mathematics
The division of 6 by the square root of 2, \(\frac{6}{\sqrt{2}}\), has significant applications in various mathematical contexts. Understanding these applications can provide insight into how mathematical principles are utilized in practical scenarios.
Here are some key applications:
- Geometry: The result of \(\frac{6}{\sqrt{2}}\) can be used to find the length of the diagonal of a square when the side length is known. If the side length of a square is 6 units, the diagonal can be calculated as \(6\sqrt{2}\).
- Trigonometry: In trigonometric functions, the value \(\frac{6}{\sqrt{2}}\) can represent the length of a leg in a 45-45-90 triangle where the hypotenuse is 6 units.
- Physics: The division is used in calculations involving vectors and their components, especially in resolving forces and motions along different axes.
- Engineering: In electrical engineering, this division is used in calculating impedances and reactances in AC circuits where the square root of 2 is a factor.
By simplifying the division \(\frac{6}{\sqrt{2}}\) to \(6\sqrt{2}/2\) or \(3\sqrt{2}\), we make these applications more accessible for further mathematical manipulation and application in real-world problems.

Common Mistakes and Misconceptions
When dealing with the division of 6 by the square root of 2, several common mistakes and misconceptions can arise. Understanding these can help in avoiding errors and improving mathematical accuracy.
- Incorrect Rationalization: One common error is failing to properly rationalize the denominator. The correct process involves multiplying both the numerator and the denominator by the square root of 2.
- Mistaking Decimal Precision: Students often misinterpret or round decimal approximations incorrectly. It's crucial to understand that √2 is an irrational number and should be treated with appropriate precision.
- Misapplication of Rules: Sometimes, students apply incorrect arithmetic rules when dealing with radicals, such as assuming √(a/b) = (√a)/(√b), which is true, but often misapplied in different contexts.
- Overlooking Simplification: Another frequent mistake is not simplifying the expression completely, leading to cumbersome and incorrect answers.
- Fraction Misconceptions: Understanding the difference between natural numbers and rational numbers is vital. Misunderstanding the values and order of fractions can lead to significant errors.
By being aware of these common mistakes and misconceptions, students can develop a more robust understanding of mathematical principles and improve their problem-solving skills.
Use of Square Root Calculators
Square root calculators are valuable tools for simplifying and calculating the square roots of various numbers. These calculators can handle perfect squares, fractions, and even complex numbers, providing accurate results and step-by-step solutions.
Here is a detailed step-by-step process on how to use a square root calculator:
-
Select the Type of Calculation: Most calculators allow you to choose between calculating the square root or the nth root of a number. Choose the appropriate option based on your needs.
-
Enter the Number: Input the number for which you want to find the square root. This can be any positive or negative number, or even a fraction.
-
Initiate the Calculation: Click the calculate button to process the input. The calculator will provide the square root or nth root of the entered number.
-
Review the Outputs: The calculator typically displays:
- The exact square root of the number.
- An approximation if the square root is not a perfect square.
- A step-by-step breakdown of the calculation.
- Information on whether the number has a perfect square root.
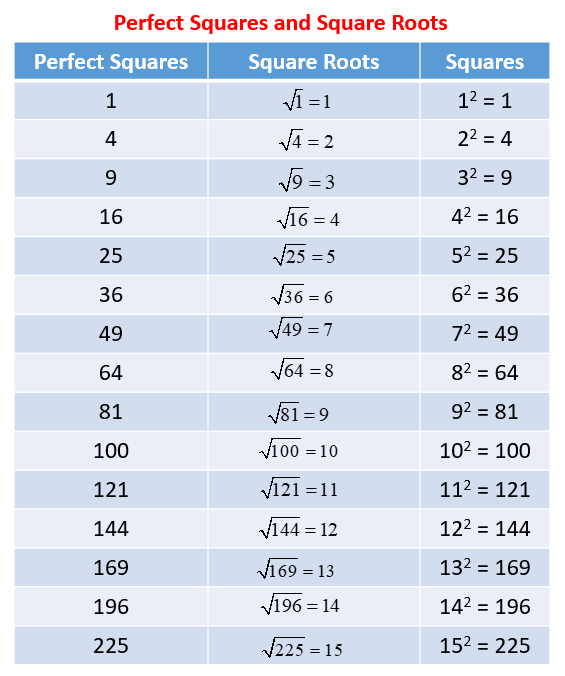
For example, to find the square root of 54, the calculator helps by showing the approximate value and step-by-step simplification:
- Recognize that 54 is between 49 (\(7^2\)) and 64 (\(8^2\)).
- Estimate that the square root of 54 is between 7 and 8.
- Refine the estimate to 7.3, since \((7.3)^2 = 53.29\) is close to 54.
This makes square root calculators essential for students and professionals dealing with complex mathematical problems.
Square Root in Different Mathematical Problems
The concept of the square root is fundamental in various mathematical problems and applications. Below, we explore different contexts where the square root is used and provide detailed examples.
-
Pythagorean Theorem
In the Pythagorean theorem, the square root is used to find the length of the hypotenuse in a right-angled triangle. If the lengths of the other two sides are \(a\) and \(b\), the hypotenuse \(c\) is given by:
\[ c = \sqrt{a^2 + b^2} \]
Example: For a triangle with sides 3 and 4, the hypotenuse is:
\[ c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
-
Quadratic Equations
The square root is crucial in solving quadratic equations. For a quadratic equation of the form \(ax^2 + bx + c = 0\), the solutions are found using the quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Example: Solving \(x^2 - 4x + 3 = 0\):
\[ x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4 \cdot 1 \cdot 3}}{2 \cdot 1} = \frac{4 \pm \sqrt{16 - 12}}{2} = \frac{4 \pm \sqrt{4}}{2} = \frac{4 \pm 2}{2} \]
This gives the solutions \(x = 3\) and \(x = 1\).
-
Geometry and Area Calculation
Square roots are often used in geometry to calculate areas and lengths. For example, the side length of a square given its area \(A\) can be found using:
\[ \text{side length} = \sqrt{A} \]
Example: For a square with area 16, the side length is:
\[ \text{side length} = \sqrt{16} = 4 \]
-
Standard Deviation in Statistics
The square root is used in statistics to calculate the standard deviation, which measures the dispersion of a set of values. The standard deviation \(\sigma\) of a dataset is given by:
\[ \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2} \]
where \(N\) is the number of values, \(x_i\) are the individual values, and \(\mu\) is the mean of the values.
-
Physics and Engineering
In physics and engineering, square roots are used in various formulas. For example, the period \(T\) of a simple pendulum is given by:
\[ T = 2\pi \sqrt{\frac{L}{g}} \]
where \(L\) is the length of the pendulum and \(g\) is the acceleration due to gravity.
Learning Resources and Tools
Understanding how to divide 6 by the square root of 2 can be greatly enhanced with various learning resources and tools. Here are some recommended tools and resources to help you grasp the concept more thoroughly:
-
Mathway: A versatile calculator that can help you find the square root of any number. It provides both exact and decimal forms of the result, making it easy to understand and verify your calculations.
Visit:
-
Omni Calculator: This tool allows you to simplify square roots and understand their properties through step-by-step examples. It’s a great way to practice simplifying roots.
Visit:
-
Third Space Learning: This site offers detailed guides and examples for understanding square numbers and roots, perfect for GCSE-level students. It includes free worksheets for practice.
Visit:
-
Elephango: A comprehensive resource for learning about perfect squares and square roots through interactive lessons and videos. It is designed for various grade levels and learning styles.
Visit:
-
Cluey Learning: Provides a list of common square roots and practical examples. It also offers personalized tutoring programs to help students master square roots.
Visit:
-
Desmos: An advanced graphing calculator that helps visualize mathematical concepts, including square roots. It’s particularly useful for interactive learning and exploration.
Visit:
Using these tools, students and enthusiasts can deepen their understanding of square roots and their applications in various mathematical problems. Whether through interactive calculators or detailed tutorials, these resources cater to a wide range of learning preferences and levels.

Conclusion and Further Reading
The division of 6 by the square root of 2, represented as \( \frac{6}{\sqrt{2}} \), is a fundamental concept in algebra that illustrates the simplification of radicals and rationalization of denominators. Simplifying this expression involves multiplying both the numerator and the denominator by \( \sqrt{2} \), which yields \( \frac{6\sqrt{2}}{2} = 3\sqrt{2} \). This process is not only a standard procedure in algebra but also a stepping stone for more advanced mathematical problems.
The exact form, \( 3\sqrt{2} \), and the decimal form, approximately 4.2426, are both useful in different contexts, whether in theoretical proofs or practical applications. Understanding and simplifying such expressions is crucial for tackling various mathematical challenges, from solving quadratic equations to integrating complex functions.
Further Reading
- : A step-by-step guide to simplifying this expression, helpful for students who need a detailed walkthrough.
- : An online tool to calculate square roots and understand the properties of square roots in algebra.
- : A video tutorial that provides a comprehensive understanding of simplifying square roots and their applications.
In conclusion, mastering the simplification of expressions involving square roots is an essential skill in mathematics. It not only aids in solving algebraic equations but also enhances your problem-solving abilities in various fields of science and engineering. For those looking to delve deeper, the resources provided offer extensive guidance and practice opportunities to strengthen your mathematical proficiency.
Căn Bậc Hai của 6
READ MORE:
Căn Bậc Hai Là Gì? | Toán Học với Thầy J