Derivative of 2 Square Root of x: Understanding and Calculation Methods

To find the derivative of the function \(2\sqrt{x}\), follow these steps:

Steps

1. Rewrite the function: \(2\sqrt{x}\) can be expressed as \(2x^{1/2}\).
2. Apply the power rule for differentiation. The power rule states that the derivative of \(x^n\) is \(nx^{n-1}\).

Calculation

Let's apply the power rule:

• Given \(f(x) = 2x^{1/2}\), we differentiate each term separately.
• The derivative of \(2x^{1/2}\) is: \[ \frac{d}{dx}[2x^{1/2}] = 2 \cdot \frac{1}{2} x^{(1/2)-1} = 2 \cdot \frac{1}{2} x^{-1/2} = x^{-1/2} \]
• Finally, rewrite \(x^{-1/2}\) as \(\frac{1}{\sqrt{x}}\).

Final Result

The derivative of \(2\sqrt{x}\) is:
\[
\frac{d}{dx}[2\sqrt{x}] = \frac{1}{\sqrt{x}}
\]

Example

For instance, if \(x = 4\):
\[
\frac{1}{\sqrt{4}} = \frac{1}{2}
\]

Conclusion

Using the power rule simplifies the differentiation process for functions involving square roots. This approach is efficient and widely applicable in calculus.

The derivative of \( 2\sqrt{x} \) involves applying the rules of calculus to find how the rate of change of this function behaves with respect to \( x \). To compute this derivative, we use fundamental techniques such as the power rule and chain rule. Understanding these methods is crucial for solving more complex problems in calculus and applying them to real-world scenarios.

When computing the derivative of \( 2\sqrt{x} \), several differentiation rules come into play:

1. Power Rule: For a function of the form \( x^n \), the derivative is \( nx^{n-1} \).
2. Chain Rule: Used for composite functions, it states that \( \frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x) \).
3. Product Rule: If differentiating a product of two functions \( u(x) \) and \( v(x) \), the rule is \( (uv)' = u'v + uv' \).
4. Quotient Rule: For differentiating the quotient of two functions \( \frac{u(x)}{v(x)} \), the formula is \( \left( \frac{u}{v} \right)' = \frac{u'v - uv'}{v^2} \).
5. First Principles Method: The derivative can also be computed directly using the definition \( f'(x) = \lim_{{h \to 0}} \frac{f(x+h) - f(x)}{h} \).

The power rule is essential for finding the derivative of \( 2\sqrt{x} \) and similar functions. According to this rule:

1. For a function of the form \( x^n \), where \( n \) is a constant, the derivative is \( nx^{n-1} \).
2. Applying it to \( 2\sqrt{x} \), we first rewrite the function as \( 2x^{1/2} \).
3. Then, applying the power rule gives us \( \frac{d}{dx}[2\sqrt{x}] = 2 \cdot \frac{1}{2} x^{(1/2)-1} = \sqrt{x} \).

The chain rule is crucial when finding the derivative of composite functions like \( 2\sqrt{x} \).

1. Consider the function \( f(x) = 2\sqrt{x} \).
2. It can be viewed as \( f(x) = 2 \cdot g(x) \) where \( g(x) = \sqrt{x} \).
3. Applying the chain rule, we differentiate \( f(x) \) as \( f'(x) = 2 \cdot g'(x) \), where \( g'(x) \) is the derivative of \( \sqrt{x} \).
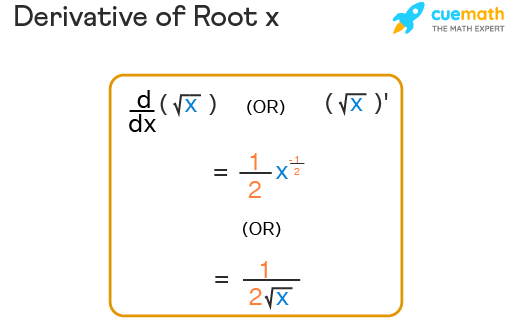
4. Derivative of \( \sqrt{x} \) using the power rule: \( g'(x) = \frac{1}{2\sqrt{x}} \).
5. Therefore, \( f'(x) = 2 \cdot \frac{1}{2\sqrt{x}} = \frac{1}{\sqrt{x}} \).

The first principles method, also known as the definition of the derivative, is fundamental for finding the derivative of \( 2\sqrt{x} \).

1. Start with the definition: \( f'(x) = \lim_{{h \to 0}} \frac{f(x+h) - f(x)}{h} \).
2. Substitute \( f(x) = 2\sqrt{x} \) into the formula.
3. Calculate \( f(x+h) \):

   \( f(x+h) \)

   = \( 2\sqrt{x+h} \)

4. Now, substitute back into the formula:

   \( f'(x) \)

   = \( \lim_{{h \to 0}} \frac{2\sqrt{x+h} - 2\sqrt{x}}{h} \)

5. Simplify the expression:

   \( f'(x) \)	= \( \lim_{{h \to 0}} \frac{2(\sqrt{x+h} - \sqrt{x})}{h} \)
   	= \( \lim_{{h \to 0}} \frac{2(\sqrt{x+h} - \sqrt{x}) \cdot (\sqrt{x+h} + \sqrt{x})}{h(\sqrt{x+h} + \sqrt{x})} \)
   	= \( \lim_{{h \to 0}} \frac{2(x+h - x)}{h(\sqrt{x+h} + \sqrt{x})} \)
   	= \( \lim_{{h \to 0}} \frac{2}{\sqrt{x+h} + \sqrt{x}} \)
   	= \( \frac{2}{2\sqrt{x}} \)
   	= \( \frac{1}{\sqrt{x}} \)

When finding the derivative of \( 2\sqrt{x} \), the product rule is applied when the function is expressed as a product of two functions.

1. Consider \( f(x) = 2 \) and \( g(x) = \sqrt{x} \).
2. Apply the product rule: \( (fg)' = f'g + fg' \).
3. Find \( f'(x) \) and \( g'(x) \):
   • For \( f(x) = 2 \), \( f'(x) = 0 \).
   • For \( g(x) = \sqrt{x} \), \( g'(x) = \frac{1}{2\sqrt{x}} \).
4. Using the product rule:

   \( (2\sqrt{x})' \)	= \( 0 \cdot \sqrt{x} + 2 \cdot \frac{1}{2\sqrt{x}} \)
   	= \( \frac{1}{\sqrt{x}} \)

The quotient rule is a formula used to find the derivative of a quotient of two functions. Given two functions \( f(x) \) and \( g(x) \), where \( g(x) \neq 0 \), the quotient rule states:

Here’s how it works step-by-step:

1. Identify the numerator \( f(x) \) and the denominator \( g(x) \).
2. Apply the quotient rule formula:

\( \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) \)

\( = \frac{g(x) \cdot f'(x) - f(x) \cdot g'(x)}{(g(x))^2} \)

3. Calculate \( f'(x) \) and \( g'(x) \), the derivatives of \( f(x) \) and \( g(x) \), respectively.
4. Multiply \( g(x) \) by \( f'(x) \) and \( f(x) \) by \( g'(x) \).
5. Subtract the results from step 4.
6. Finally, divide the result from step 5 by \( (g(x))^2 \).

The quotient rule is particularly useful when dealing with functions that are expressed as a ratio, allowing us to find their derivatives efficiently.

Let's work through some examples and practice problems involving the derivative of \( 2 \sqrt{x} \).

1. Example 1:

Find the derivative of \( y = 2 \sqrt{x} \).

\( y = 2 \sqrt{x} \)	\( \Rightarrow \)	\( y' = \frac{d}{dx} (2 \sqrt{x}) \)
		\( y' = 2 \cdot \frac{1}{2\sqrt{x}} \) (using the power rule)
		\( y' = \frac{1}{\sqrt{x}} \)

2. Example 2:

Find the derivative of \( f(x) = \frac{2}{\sqrt{x}} \).

\( f(x) = \frac{2}{\sqrt{x}} \)	\( \Rightarrow \)	\( f'(x) = \frac{d}{dx} \left( \frac{2}{\sqrt{x}} \right) \)
		\( f'(x) = 2 \cdot \frac{d}{dx} (x^{-\frac{1}{2}}) \) (using the constant multiple rule)
		\( f'(x) = 2 \cdot (-\frac{1}{2}) x^{-\frac{3}{2}} \) (using the power rule)
		\( f'(x) = -\frac{1}{\sqrt{x^3}} \)

The derivative of \( 2 \sqrt{x} \) finds applications in various real-world scenarios:

1. Physics: In mechanics, the velocity \( v(t) \) of an object falling under gravity near Earth’s surface can be described by \( v(t) = 2 \sqrt{gt} \), where \( g \) is the acceleration due to gravity and \( t \) is time. The derivative \( v'(t) \) gives the acceleration of the object.
2. Engineering: In structural engineering, the rate of change of stress concentration around a circular hole in a plate, represented by \( \sigma(x) = 2 \sqrt{\frac{K}{\pi} x} \), helps engineers optimize designs for maximum strength.
3. Economics: The marginal cost \( MC(q) \) of producing \( q \) units of a product in a market with increasing costs can be modeled by \( MC(q) = 2 \sqrt{q} \), where the derivative \( MC'(q) \) provides insights into cost efficiency and pricing strategies.
4. Biology: In population biology, the growth rate of a population \( P(t) \) can be approximated by \( P'(t) = 2 \sqrt{kP(t)} \), where \( k \) is a constant related to environmental factors affecting growth.