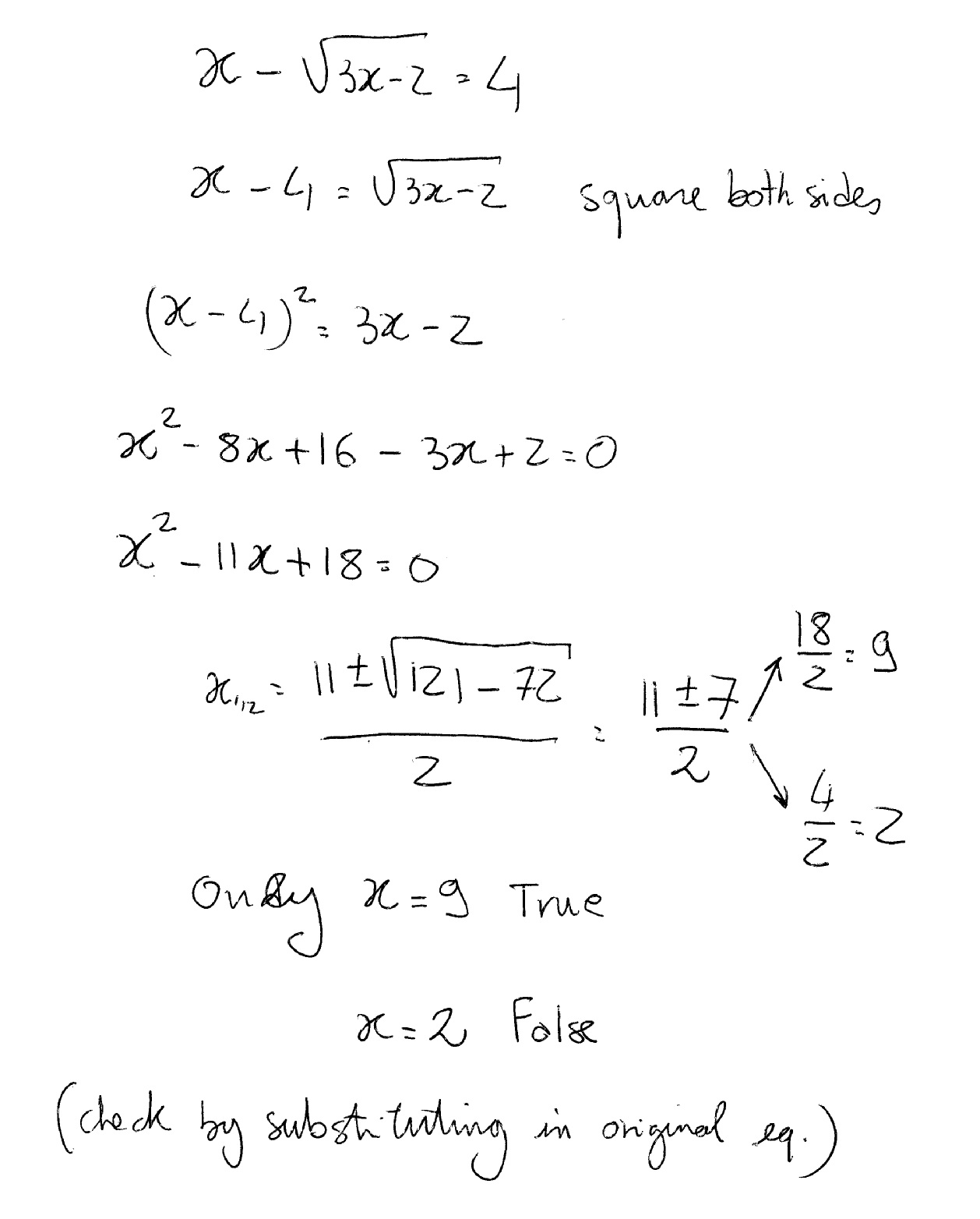Topic 2 x square root of 3: Understanding the mathematical concept of "2 x square root of 3" is essential for various applications in algebra and beyond. This article explores its calculation, significance, and practical applications in a clear and concise manner, making complex math accessible to everyone. Dive in to enhance your math skills and grasp this fundamental concept with ease.
Table of Content
- Simplification of 2 × Square Root of 3
- Introduction
- Table of Contents
- Definition and Basic Explanation
- Mathematical Simplification
- Calculations and Exact Forms
- Applications in Algebra
- Advanced Examples
- Interactive Calculators and Tools
- Conclusion
- Definition and Basic Explanation
- Mathematical Simplification
- Calculations and Exact Forms
- Applications in Algebra
- Advanced Examples
- Interactive Calculators and Tools
- YOUTUBE: Xem video này để học cách phân tích đa thức x^2 - 2√3 x - 24. Video cung cấp hướng dẫn chi tiết và dễ hiểu cho học sinh.
Simplification of 2 × Square Root of 3
The mathematical expression 2 × √3 can be simplified as follows:
- Exact Form: \(2\sqrt{3}\)
- Decimal Form: \(2\sqrt{3} \approx 3.464\)
Steps to Simplify
To simplify the expression \(2\sqrt{3}\), follow these steps:
Identify the constant and the square root: The expression consists of the constant 2 and the square root of 3.
Combine them as a single term: When multiplied, they remain as \(2\sqrt{3}\).
Decimal approximation: Use a calculator to find the approximate decimal value. \(2\sqrt{3} \approx 3.464\).
Examples of Similar Simplifications
Here are a few examples of similar simplifications:
- \(\sqrt{12}\): Simplified to \(2\sqrt{3}\)
- \(\sqrt{18}\): Simplified to \(3\sqrt{2}\)
- \(\sqrt{45}\): Simplified to \(3\sqrt{5}\)
Understanding the Process
Simplifying square roots involves factoring the number inside the square root to its prime factors and then applying the square root to each factor. The goal is to make the expression as simple as possible.
| Expression | Simplification |
|---|---|
| \(\sqrt{12}\) | \(2\sqrt{3}\) |
| \(\sqrt{18}\) | \(3\sqrt{2}\) |
| \(\sqrt{45}\) | \(3\sqrt{5}\) |
Conclusion
To simplify the expression \(2\sqrt{3}\), recognize that it is already in its simplest form. The exact value is \(2\sqrt{3}\), and its decimal approximation is approximately 3.464.

READ MORE:
Introduction
The expression
In mathematics, the square root of a number \(x\) is a value that, when multiplied by itself, gives the number \(x\). For example, the square root of 9 is 3, since \(3^2 = 9\). When dealing with expressions like \(2 \times \sqrt{3}\), it's important to apply the correct rules of algebra to simplify and understand the result.
This introduction sets the stage for a deeper dive into the methods used to simplify square roots, the multiplication and division of radicals, and practical applications of these concepts in solving algebraic equations. By mastering these techniques, readers will enhance their mathematical proficiency and problem-solving abilities.
Table of Contents
Definition and Basic Explanation
Understanding the expression \(2 \sqrt{3}\), which represents two times the square root of three. This section will define and explain the components and the significance of this mathematical term.
Mathematical Simplification
Simplifying Square Roots: The process of simplifying square roots by factoring out perfect squares.
Example: Simplify \(2 \sqrt{3}\): Detailed step-by-step simplification of \(2 \sqrt{3}\).

Calculations and Exact Forms
Exact Form Calculation: Expressing \(2 \sqrt{3}\) in its exact form using radical notation.
Decimal Form Calculation: Converting \(2 \sqrt{3}\) into its decimal form for practical use.
Applications in Algebra
Use in Algebraic Expressions: How \(2 \sqrt{3}\) can be used in various algebraic contexts.
Multiplication and Division of Radicals: Rules and examples for multiplying and dividing square roots, including \(2 \sqrt{3}\).
Advanced Examples
Combining and Simplifying Multiple Square Roots: Techniques for handling complex expressions involving multiple square roots.
Example: Simplify \(\sqrt{12}\) as \(2 \sqrt{3}\): Step-by-step simplification of \(\sqrt{12}\) to show its relation to \(2 \sqrt{3}\).
Interactive Calculators and Tools
Online Square Root Calculators: A review of useful online tools for calculating square roots.
Step-by-Step Calculation Tools: Resources that provide step-by-step solutions for simplifying expressions like \(2 \sqrt{3}\).
Conclusion
A summary of the key points discussed and the importance of understanding the expression \(2 \sqrt{3}\) in various mathematical contexts.
Definition and Basic Explanation
The expression \(2 \times \sqrt{3}\) combines basic operations with a square root. To understand this expression, it's important to break it down into its components: the number 2 and the square root of 3.
The square root of a number \(x\) is a value that, when multiplied by itself, gives \(x\). It is denoted by the radical symbol \( \sqrt{} \). For example, the square root of 9 is 3, because \(3 \times 3 = 9\).
In mathematical terms, the square root of 3 is written as \( \sqrt{3} \). Since 3 is not a perfect square, its square root is an irrational number, approximately equal to 1.732. Thus, \( \sqrt{3} \approx 1.732 \).
When we multiply 2 by \( \sqrt{3} \), we are essentially scaling the value of \( \sqrt{3} \) by 2. Therefore, \( 2 \times \sqrt{3} \) is approximately \( 2 \times 1.732 = 3.464 \).
In summary, \(2 \times \sqrt{3}\) represents the multiplication of the integer 2 by the irrational number \( \sqrt{3} \), resulting in another irrational number. This concept is frequently used in various mathematical problems and applications, especially those involving geometry and algebra.
Mathematical Simplification
Mathematical simplification involves reducing expressions to their simplest form. For the expression \( 2 \sqrt{3} \), we can follow a few basic steps to understand its simplification process.
Simplifying Square Roots
To simplify a square root, we look for perfect square factors within the number under the root. The goal is to express the number inside the square root as a product of a perfect square and another number.
For example, consider the square root of 12:
- Identify factors: \( 12 = 4 \times 3 \)
- Apply the square root: \( \sqrt{12} = \sqrt{4 \times 3} \)
- Separate the square roots: \( \sqrt{4} \times \sqrt{3} \)
- Simplify the perfect square: \( 2 \sqrt{3} \)
Thus, \( \sqrt{12} \) simplifies to \( 2 \sqrt{3} \).
Example: Simplify \( 2 \sqrt{3} \)
The expression \( 2 \sqrt{3} \) is already in its simplest form because the square root of 3 cannot be simplified further as 3 is not a perfect square. Therefore, \( 2 \sqrt{3} \) remains unchanged.
Further Examples
- Simplifying \( \sqrt{18} \):
- Identify factors: \( 18 = 9 \times 2 \)
- Apply the square root: \( \sqrt{18} = \sqrt{9 \times 2} \)
- Separate the square roots: \( \sqrt{9} \times \sqrt{2} \)
- Simplify the perfect square: \( 3 \sqrt{2} \)
- Simplifying \( \sqrt{45} \):
- Identify factors: \( 45 = 9 \times 5 \)
- Apply the square root: \( \sqrt{45} = \sqrt{9 \times 5} \)
- Separate the square roots: \( \sqrt{9} \times \sqrt{5} \)
- Simplify the perfect square: \( 3 \sqrt{5} \)
Combining and Simplifying Multiple Square Roots
When combining and simplifying multiple square roots, we can multiply the square roots together and then simplify:
- Example: \( \sqrt{6} \times \sqrt{15} \):
- Combine under a single square root: \( \sqrt{6 \times 15} \)
- Simplify the product: \( \sqrt{90} \)
- Identify factors: \( 90 = 9 \times 10 \)
- Separate and simplify: \( \sqrt{9} \times \sqrt{10} = 3 \sqrt{10} \)
By understanding these principles, you can simplify any square root expression effectively.
Calculations and Exact Forms
The expression \(2 \sqrt{3}\) can be represented in both exact and decimal forms. Below are detailed steps for calculating and converting between these forms.
Exact Form Calculation
The exact form of the expression is simply the expression itself, as it involves a radical which is irrational and cannot be expressed as a finite decimal or fraction.
- Start with the expression: \(2 \sqrt{3}\)
- This is already in its exact form.
- Example: \(2 \sqrt{3}\)
Decimal Form Calculation
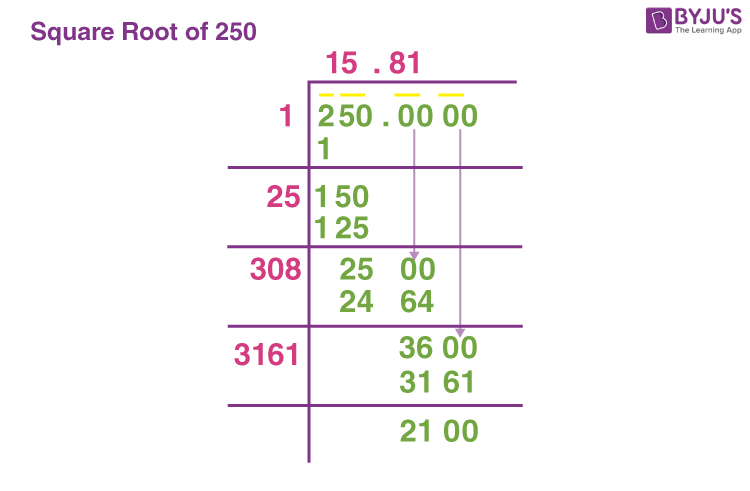
To convert the expression to its decimal form, we approximate the value of the square root of 3 and then multiply by 2.
- Approximate the value of \(\sqrt{3}\):
- \(\sqrt{3} \approx 1.732\)
- Multiply by 2:
- \(2 \times 1.732 = 3.464\)
Therefore, the decimal form of \(2 \sqrt{3}\) is approximately 3.464.
Steps Using a Calculator
Using an online square root calculator simplifies the process:
- Enter the number 3 into the square root calculator to get \(\sqrt{3} \approx 1.732\).
- Multiply the result by 2 to obtain the final value, which is approximately 3.464.
Applications and Examples
The expression \(2 \sqrt{3}\) appears in various mathematical contexts:
- Geometry: It can represent lengths and distances, especially in triangles and other geometric shapes.
- Algebra: Used in solving equations and simplifying expressions involving radicals.
Interactive Tools
Online calculators, such as those provided by CalculatorSoup and BYJU'S, can help verify calculations and explore more examples. These tools offer step-by-step solutions for better understanding.
Applications in Algebra
The expression \(2 \sqrt{3}\) appears frequently in algebraic contexts, providing a basis for understanding various operations involving radicals. Below are some key applications:
Use in Algebraic Expressions
In algebra, \(2 \sqrt{3}\) can be used within more complex expressions. For example, it can be combined with other radicals or constants in polynomial equations:
Example: Solve for \(x\) in \(x^2 + 2 \sqrt{3} x + 3 = 0\).
By applying the quadratic formula \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\), we solve:
\(x = \frac{-2 \sqrt{3} \pm \sqrt{(2 \sqrt{3})^2 - 4 \cdot 1 \cdot 3}}{2 \cdot 1} = \frac{-2 \sqrt{3} \pm \sqrt{12 - 12}}{2} = \frac{-2 \sqrt{3}}{2} = - \sqrt{3}\).
Multiplication and Division of Radicals
Radicals can be multiplied and divided by utilizing properties of square roots. For \(2 \sqrt{3}\), this includes:
Multiplication: \(2 \sqrt{3} \cdot \sqrt{6} = 2 \sqrt{3 \cdot 6} = 2 \sqrt{18} = 2 \cdot 3 \sqrt{2} = 6 \sqrt{2}\).
Division: \(\frac{2 \sqrt{3}}{\sqrt{3}} = 2\).
Understanding these applications helps in solving equations and simplifying expressions involving radicals.
Advanced Examples
In this section, we explore advanced examples of working with the expression \(2 \times \sqrt{3}\). We will look at combining and simplifying multiple square roots, and how to handle more complex radical expressions.
Combining and Simplifying Multiple Square Roots
When working with multiple square roots, we often need to combine or simplify them to make calculations easier. One useful property is that the product of square roots can be simplified:
\[
\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}
\]
For example:
- \(\sqrt{2} \times \sqrt{8} = \sqrt{16} = 4\)
- \(\sqrt{3} \times \sqrt{12} = \sqrt{36} = 6\)
Example: Simplify \(2\sqrt{3}\)
Let's simplify the expression \(2 \times \sqrt{3}\).
- Identify the constants and the square root: \(2\) and \(\sqrt{3}\).
- Combine the constants and the square roots if possible: \(2\) is already simplified, and \(\sqrt{3}\) is in its simplest form.
- Therefore, \(2 \times \sqrt{3}\) is already simplified.
Example: Simplify \(\sqrt{12}\) as \(2\sqrt{3}\)
Consider the square root of \(12\). We can simplify it as follows:
- Factor \(12\) into its prime factors: \(12 = 2^2 \times 3\).
- Express the square root using these factors: \(\sqrt{12} = \sqrt{2^2 \times 3}\).
- Use the property of square roots to separate the factors: \(\sqrt{2^2} \times \sqrt{3} = 2 \times \sqrt{3}\).
- Therefore, \(\sqrt{12} = 2 \times \sqrt{3}\).
Example: Simplifying More Complex Expressions
For more complex expressions, such as \(\sqrt{75} - 2\sqrt{3}\), follow these steps:
- Simplify each square root individually: \(\sqrt{75} = \sqrt{25 \times 3} = 5\sqrt{3}\).
- Combine like terms: \(5\sqrt{3} - 2\sqrt{3} = (5 - 2)\sqrt{3} = 3\sqrt{3}\).
Example: Rationalizing the Denominator
When an expression has a radical in the denominator, we often need to rationalize it. For example, simplify \(\frac{1}{\sqrt{3}}\):
- Multiply the numerator and the denominator by \(\sqrt{3}\): \(\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}\).
- The result is \(\frac{\sqrt{3}}{3}\), which is the rationalized form.
Interactive Calculators and Tools
Interactive calculators and tools can greatly enhance the understanding and computation of mathematical expressions such as "2 x square root of 3". Here are some useful tools that can help with various calculations involving square roots:
-
Square Root Calculators
These calculators allow you to input any number and find its square root. If the number is not a perfect square, the calculator provides both the exact form and the decimal approximation.
- - A comprehensive calculator that covers various mathematical functions, including square roots.
- - Offers step-by-step solutions for square roots and other algebraic problems.
- - Simplifies square roots and explains the process step-by-step.
-
Graphing Calculators
Graphing calculators can plot the functions involving square roots and visualize the solutions. These tools are beneficial for understanding the graphical representation of equations.
- - A powerful graphing tool that can handle complex algebraic expressions, including those with square roots.
-
Step-by-Step Calculation Tools
These tools provide detailed steps for solving problems involving square roots, which can help students understand the underlying principles and processes.
- - Offers detailed step-by-step solutions for a wide range of mathematical problems.
- - Provides comprehensive step-by-step explanations for solving square roots and other algebraic functions.
Xem video này để học cách phân tích đa thức x^2 - 2√3 x - 24. Video cung cấp hướng dẫn chi tiết và dễ hiểu cho học sinh.
Phân tích đa thức x^2 - 2√3 x - 24
READ MORE:
Tìm hiểu lý do tại sao biểu thức 'x mũ 1/2' lại đại diện cho căn bậc hai trong toán học. Khám phá kiến thức thú vị này!
Tại sao "x mũ 1/2" có nghĩa là căn bậc hai?