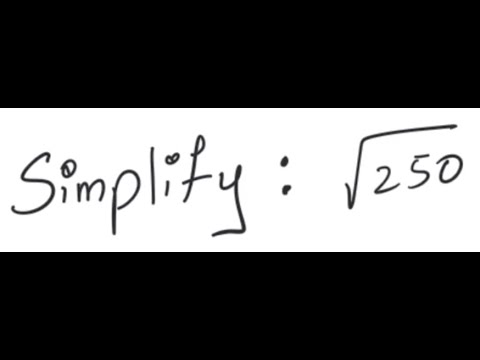Topic 5 square root of 2: The concept of the square root is fundamental in mathematics, and understanding how to simplify expressions like "5 square root of 2" can be incredibly useful. This article explores the calculation, applications, and significance of 5√2, providing clear steps and insights to help you master this mathematical operation.
Table of Content
- Understanding 5 Square Root of 2
- Introduction
- Basic Definition of Square Root
- Understanding 5 Square Root of 2
- Mathematical Representation
- Simplifying Square Roots
- Examples of Simplified Square Roots
- Applications in Algebra
- Decimal and Exact Forms
- Calculating Square Roots
- Perfect Squares and their Roots
- Square Root Properties
- Special Cases in Square Roots
- Conclusion
- YOUTUBE: Hướng dẫn cách tính tích của căn bậc hai của hai số, √(5) và √(50), giúp bạn hiểu rõ hơn về các bước thực hiện và ứng dụng trong toán học.
Understanding 5 Square Root of 2
The expression represents five times the square root of two. Here’s a detailed explanation:
Exact and Decimal Form
Square Root Simplification
Simplifying square roots is a key algebraic skill:
- Exact form: The expression remains .
- Decimal form: Approximating the square root of 2 (approximately 1.414), the expression becomes approximately 7.071.
Using a Calculator
To find the decimal form quickly, you can use an online calculator:
| Enter the expression into a square root calculator. |
Understanding Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number:
- For example, the square root of 9 is 3 because 32 = 9.
- Similarly, is a value that when squared gives 2, which is approximately 1.414.
Additional Resources
For more information on simplifying radicals and square roots, you can check out these resources:
READ MORE:
Introduction
The expression \(5 \sqrt{2}\) combines a whole number with an irrational number, resulting in an interesting mathematical concept that has various applications. In this introduction, we will explore the significance of the square root of 2, its mathematical properties, and the relevance of multiplying it by 5. This topic is fundamental in algebra and number theory, providing a stepping stone to more advanced mathematical concepts.
Basic Definition of Square Root
The square root of a number is a value that, when multiplied by itself, gives the original number. The square root symbol is denoted as √. For example, the square root of 25 is 5 because 5 × 5 = 25. This concept is fundamental in mathematics and is used in various fields such as algebra, geometry, and calculus.
The principal square root is always non-negative. For any non-negative number \( a \), the principal square root is written as \( \sqrt{a} \). If \( b \) is the square root of \( a \), then it satisfies the equation \( b^2 = a \).
To simplify square roots, one can use the property \( \sqrt{a \times b} = \sqrt{a} \times \sqrt{b} \). This property helps in breaking down the square root of a product into the product of the square roots of its factors.
- Example: Simplify \( \sqrt{45} \). Since 45 can be factored into 9 and 5, and 9 is a perfect square, we have:
- Write 45 as a product of 9 and 5: \( 45 = 9 \times 5 \)
- Use the property of square roots: \( \sqrt{45} = \sqrt{9 \times 5} = \sqrt{9} \times \sqrt{5} \)
- Simplify the square root of 9: \( \sqrt{9} = 3 \)
- Combine the results: \( \sqrt{45} = 3\sqrt{5} \)
- Note: Not all square roots can be simplified to an exact integer. For instance, \( \sqrt{2} \) is an irrational number and cannot be simplified further.
| Number | Square Root |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
Understanding 5 Square Root of 2
To understand the expression \( 5\sqrt{2} \), let's break it down into its components and explore its meaning, calculation, and applications.
The expression \( 5\sqrt{2} \) consists of two parts:
- 5: This is a scalar multiplier.
- \(\sqrt{2}\): This is the square root of 2.
When combined, \( 5\sqrt{2} \) means that the square root of 2 is multiplied by 5.
Mathematical Representation
In mathematical notation, the square root of 2 is represented as \( \sqrt{2} \). Therefore, \( 5\sqrt{2} \) can be represented as:
\[
5\sqrt{2}
\]
Calculating the Value
The square root of 2 is an irrational number approximately equal to 1.414. Thus, we can approximate \( 5\sqrt{2} \) as follows:
\[
5 \times 1.414 \approx 7.07
\]
So, \( 5\sqrt{2} \approx 7.07 \) in decimal form.
Exact and Decimal Forms
The exact form of the expression is \( 5\sqrt{2} \), while the decimal form is approximately 7.07. It's important to use the exact form in mathematical proofs and derivations, whereas the decimal form is useful for practical calculations.
Properties of \( 5\sqrt{2} \)
- It is an irrational number because \( \sqrt{2} \) is irrational.
- It is not a perfect square.
- It can be represented in both exact and decimal forms.
Applications
Expressions like \( 5\sqrt{2} \) are commonly used in various fields, including:
- Geometry: Calculating lengths in right triangles where one side is a multiple of \( \sqrt{2} \).
- Physics: Describing wave functions and other phenomena that involve irrational numbers.
- Engineering: Solving problems that involve precise measurements and root calculations.
Simplifying Radicals
In some cases, you might need to simplify radical expressions. While \( 5\sqrt{2} \) is already in its simplest form, other expressions can be simplified using various mathematical techniques.
Understanding \( 5\sqrt{2} \) is fundamental to grasping more complex mathematical concepts and solving practical problems efficiently.
Mathematical Representation
The expression \(5\sqrt{2}\) represents the product of 5 and the square root of 2. Below, we will explore its mathematical representation in both exact and approximate forms.
Exact Form
The exact form of the expression is simply written as:
\[
5\sqrt{2}
\]
Decimal Form
The square root of 2 is an irrational number, approximately equal to 1.41421. Therefore, multiplying this by 5 gives:
\[
5 \times 1.41421 \approx 7.07107
\]
Geometric Interpretation
Geometrically, \(5\sqrt{2}\) can be understood in the context of right-angled triangles. According to the Pythagorean theorem, if one leg of a right triangle is 5 units and the other leg is \(5\sqrt{2}\) units, the hypotenuse will be:
\[
\sqrt{(5^2) + (5\sqrt{2})^2} = \sqrt{25 + 50} = \sqrt{75} = 5\sqrt{3}
\]
Representation in Algebra
In algebra, \(5\sqrt{2}\) often appears in equations and expressions involving radicals. For instance, in solving quadratic equations, simplifying expressions, and during rationalization processes.
Applications
- Geometry: \(5\sqrt{2}\) is useful in problems involving distances and measurements, such as finding the length of the diagonal in squares and rectangles.
- Trigonometry: It appears in the context of solving trigonometric functions where square roots are involved.
- Physics and Engineering: Used in calculations involving wave lengths, signal processing, and other applied physics scenarios.
Conclusion
The expression \(5\sqrt{2}\) is a fundamental mathematical concept with wide-ranging applications in various fields, from theoretical mathematics to practical engineering problems. Its representation, whether exact or approximate, helps in simplifying and solving complex mathematical problems.

Simplifying Square Roots
Square roots can often be simplified to make them easier to work with. Simplifying a square root involves finding the prime factors of the number under the square root sign and then determining pairs of factors. Here’s a step-by-step process for simplifying square roots:
- Identify the number under the square root sign.
- Find the prime factorization of the number.
- Group the factors into pairs of identical factors.
- Move one of each pair of identical factors outside the square root sign.
- Multiply the factors outside the square root sign together to get the simplified square root.
- If any factors are left inside the square root sign, they remain under the square root.
For example, let's simplify
- Identify the number under the square root sign: 50.
- Find the prime factorization of 50: 50 = 2 × 5 × 5.
- Group the factors into pairs of identical factors: 50 = 2 × (5 × 5).
- Move one of each pair of identical factors outside the square root sign:
√(2 × 5²) = 5√2 . - There are no more pairs, so the simplified form of
√50 is5√2 .
Another example is
- Identify the number under the square root sign: 72.
- Find the prime factorization of 72: 72 = 2 × 2 × 2 × 3 × 3.
- Group the factors into pairs of identical factors: 72 = (2 × 2) × 2 × (3 × 3).
- Move one of each pair of identical factors outside the square root sign:
√(2² × 2 × 3²) = 2 × 3√2 = 6√2 . - There are no more pairs, so the simplified form of
√72 is6√2 .
By following these steps, you can simplify most square roots, making calculations and expressions more manageable.
Examples of Simplified Square Roots
To understand how to simplify square roots, let's look at some specific examples. These examples will illustrate the process of finding the prime factors, grouping them, and simplifying the square roots step-by-step.
Example 1: Simplifying
- Identify the number under the square root sign: 18.
- Find the prime factorization of 18: 18 = 2 × 3 × 3.
- Group the factors into pairs of identical factors: 18 = 2 × (3 × 3).
- Move one of each pair of identical factors outside the square root sign:
√(2 × 3²) = 3√2 . - There are no more pairs, so the simplified form of
√18 is3√2 .
Example 2: Simplifying
- Identify the number under the square root sign: 32.
- Find the prime factorization of 32: 32 = 2 × 2 × 2 × 2 × 2.
- Group the factors into pairs of identical factors: 32 = (2 × 2) × (2 × 2) × 2.
- Move one of each pair of identical factors outside the square root sign:
√(2² × 2² × 2) = 2 × 2√2 = 4√2 . - There are no more pairs, so the simplified form of
√32 is4√2 .
Example 3: Simplifying
- Identify the number under the square root sign: 5.
- Recognize that 5 is already a prime number, so it cannot be simplified further.
- Understand that
5√2 is already in its simplest form because 5 is a coefficient and 2 is under the square root sign.
Example 4: Simplifying
- Identify the number under the square root sign: 72.
- Find the prime factorization of 72: 72 = 2 × 2 × 2 × 3 × 3.
- Group the factors into pairs of identical factors: 72 = (2 × 2) × 2 × (3 × 3).
- Move one of each pair of identical factors outside the square root sign:
√(2² × 2 × 3²) = 2 × 3√2 = 6√2 . - There are no more pairs, so the simplified form of
√72 is6√2 .
These examples demonstrate how to simplify square roots by breaking down the number into its prime factors, grouping them, and moving pairs outside the square root sign. Practice with these and similar examples to become proficient at simplifying square roots.
Applications in Algebra
The concept of square roots, including expressions like
1. Solving Quadratic Equations
Square roots are commonly used in solving quadratic equations. The quadratic formula, which is used to find the roots of a quadratic equation
For example, to solve
- Identify
a = 1 ,b = -6 , andc = 8 . - Substitute into the quadratic formula:
x = \frac{{6 \pm \sqrt{{(-6)^2 - 4 \cdot 1 \cdot 8}}}}{2 \cdot 1} . - Simplify under the square root:
x = \frac{{6 \pm \sqrt{36 - 32}}}{2} = \frac{{6 \pm \sqrt{4}}}{2} . - Calculate the roots:
x = \frac{{6 \pm 2}}{2} , givingx = 4 orx = 2 .
2. Simplifying Radical Expressions
Expressions involving square roots can often be simplified to make algebraic manipulation easier. For instance, combining like terms with square roots:
This simplification is useful in solving equations and in polynomial operations.
3. Rationalizing the Denominator
Square roots often appear in fractions, and it is a common practice to rationalize the denominator. For example:
- Consider the fraction
\frac{1}{√2} . - Multiply the numerator and the denominator by
√2 to eliminate the square root in the denominator:\frac{1}{√2} \times \frac{√2}{√2} = \frac{√2}{2} .
4. Working with Complex Numbers
In algebra, square roots of negative numbers are defined using the imaginary unit
This concept is essential in advanced algebra and calculus.
5. Polynomial Functions
Square roots are used in polynomial functions and their transformations. For example, the function
These applications highlight the importance of understanding and manipulating square roots in algebra. Mastery of these concepts allows for solving a wide range of algebraic problems efficiently.
Decimal and Exact Forms
Understanding both the decimal and exact forms of the expression \(5 \sqrt{2}\) can provide a clearer grasp of its value in different contexts.
Exact Form
The exact form of the expression \(5 \sqrt{2}\) is left as is because \(\sqrt{2}\) is an irrational number, which means it cannot be expressed as a precise fraction or a terminating or repeating decimal. The exact form is:
\[
5 \sqrt{2}
\]
Decimal Form
To find the decimal form, we can approximate \(\sqrt{2}\). The value of \(\sqrt{2}\) is approximately 1.414213562. Multiplying this by 5 gives us:
\[
5 \times 1.414213562 \approx 7.071067811
\]
Thus, the decimal form of \(5 \sqrt{2}\) is approximately 7.071. Note that this is a rounded value and the digits continue indefinitely without repeating.
Comparison Table
Here is a table comparing the exact form and its decimal approximation:
| Exact Form | Decimal Form |
|---|---|
| \(5 \sqrt{2}\) | 7.071067811... |
Calculation Steps
To manually calculate the decimal form of \(5 \sqrt{2}\), follow these steps:
- Approximate the value of \(\sqrt{2}\), which is about 1.414213562.
- Multiply this approximation by 5:
\[
5 \times 1.414213562 = 7.071067811
\]
Practical Use
Using the decimal form can be practical in everyday calculations, where an approximate value is sufficient. However, in more precise mathematical work, the exact form is preferred to maintain accuracy.
By understanding both forms, one can switch between precision and practicality as needed.

Calculating Square Roots
To calculate the square root of a number, such as \( 5\sqrt{2} \), follow these steps:
- Estimate the square root: Determine a close approximation for \( \sqrt{2} \). The value of \( \sqrt{2} \) is approximately 1.414.
- Multiply the estimated value by 5: \( 5 \times 1.414 = 7.07 \).
Therefore, \( 5\sqrt{2} \approx 7.07 \).
Perfect Squares and their Roots
A perfect square is a number that can be expressed as the square of an integer. Here are some examples:
- \( 1^2 = 1 \)
- \( 2^2 = 4 \)
- \( 3^2 = 9 \)
- \( 4^2 = 16 \)
- \( 5^2 = 25 \)
- \( 6^2 = 36 \)
- \( 7^2 = 49 \)
- \( 8^2 = 64 \)
- \( 9^2 = 81 \)
- \( 10^2 = 100 \)
The square roots of these perfect squares are:
| \( \sqrt{1} = 1 \) | \( \sqrt{4} = 2 \) | \( \sqrt{9} = 3 \) |
| \( \sqrt{16} = 4 \) | \( \sqrt{25} = 5 \) | \( \sqrt{36} = 6 \) |
| \( \sqrt{49} = 7 \) | \( \sqrt{64} = 8 \) | \( \sqrt{81} = 9 \) |
| \( \sqrt{100} = 10 \) |
Square Root Properties
Understanding the properties of square roots helps in various mathematical applications. Here are some key properties:
- \( \sqrt{a} \cdot \sqrt{b} = \sqrt{ab} \)
- \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \)
- \( \sqrt{a^2} = |a| \), where \( |a| \) denotes the absolute value of \( a \)
- \( \sqrt{a \cdot a} = a \), for any non-negative real number \( a \)
These properties are essential in simplifying expressions involving square roots and in solving equations where square roots are present.
Special Cases in Square Roots
There are several special cases to consider when dealing with square roots:
- Square roots of negative numbers are considered imaginary and are denoted by \( \sqrt{-a} = i \sqrt{a} \), where \( i \) is the imaginary unit.
- Square roots of zero and one have specific values: \( \sqrt{0} = 0 \) and \( \sqrt{1} = 1 \).
- For any non-negative real number \( a \), \( \sqrt{a^2} = a \).
- When simplifying square roots, it's crucial to consider the principal square root, denoted by \( \sqrt{a} \geq 0 \).
Understanding these cases helps in navigating through various mathematical problems involving square roots.
Conclusion
Understanding the concept of the square root, particularly , and its applications is fundamental in various fields of mathematics and science. The expression provides a valuable example of how square roots can be scaled and manipulated.
Key takeaways include:
- The basic definition of square roots helps in simplifying complex expressions.
- Understanding how to represent and simplify square roots, such as , is crucial for solving algebraic problems.
- Square roots have applications in algebra, making it easier to handle quadratic equations and other polynomial expressions.
- Recognizing the decimal and exact forms of square roots aids in precise calculations.
- Knowledge of perfect squares and their roots simplifies the process of identifying square roots.
- Square root properties and special cases expand our understanding of mathematical relationships and functions.
Overall, mastering the concept of and square roots in general equips students and professionals with essential skills for advanced mathematical problem-solving. By building a strong foundation in these principles, one can confidently tackle more complex mathematical challenges.
Hướng dẫn cách tính tích của căn bậc hai của hai số, √(5) và √(50), giúp bạn hiểu rõ hơn về các bước thực hiện và ứng dụng trong toán học.
Cách tìm tích của căn bậc hai của hai số, √(5) . √(50)
READ MORE:
Tìm hiểu cách giảm 5 căn bậc hai của 2 về một căn đơn giản hơn trong video này, với các bước chi tiết và dễ hiểu.
5 căn bậc hai của 2, giảm về một căn, giảm về một căn thức