Topic 225 square root: Discover the fascinating world of the 225 square root. This comprehensive guide covers everything from basic calculations to practical applications. Learn why 225 is a perfect square, explore methods to find its square root, and understand its significance in various fields. Perfect for students, educators, and math enthusiasts.
Table of Content
- Understanding the Square Root of 225
- Introduction to Square Roots
- What is the Square Root of 225?
- Methods to Calculate the Square Root of 225
- Understanding Perfect Squares
- Applications of the Square Root of 225
- Square Root Function in Mathematics
- Historical Context of Square Roots
- Common Mistakes and Misconceptions
- Practice Problems and Solutions
- YOUTUBE: Video hướng dẫn cách tìm căn bậc hai của 225 bằng phương pháp phân tích thừa số nguyên tố. Tìm hiểu về căn bậc hai của 225 và áp dụng nó trong toán học.
Understanding the Square Root of 225
The square root of a number is a value that, when multiplied by itself, gives the original number. In mathematical notation, the square root is represented by the radical symbol √.
Calculating the Square Root of 225
The number 225 is a perfect square, which means its square root is an integer. To find the square root of 225, we look for a number that, when multiplied by itself, equals 225.
The equation is:
\[ \sqrt{225} = x \]
We need to find \( x \) such that:
\[ x \times x = 225 \]
By testing integers or using the properties of squares, we find that:
\[ 15 \times 15 = 225 \]
Therefore,
\[ \sqrt{225} = 15 \]
Properties of the Square Root of 225
- The square root of 225 is 15.
- Since 225 is a perfect square, its square root is an integer.
- The square root function is the inverse of squaring a number.
Applications of Square Roots
Square roots are used in various fields such as geometry, algebra, physics, and engineering. For example, in geometry, the length of the side of a square with an area of 225 square units can be found using the square root:
If the area \( A \) of a square is 225, then:
\[ A = s^2 \]
where \( s \) is the side length of the square.
Solving for \( s \):
\[ s = \sqrt{A} = \sqrt{225} = 15 \]
Thus, the side length of the square is 15 units.
Conclusion
The square root of 225 is a fundamental mathematical concept with practical applications in various disciplines. Knowing that \(\sqrt{225} = 15\) helps in solving problems involving area, quadratic equations, and more.

READ MORE:
Introduction to Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. It is one of the fundamental operations in mathematics and is denoted by the radical symbol √. For example, the square root of 225 is written as √225.
Square roots have numerous applications in various fields, including geometry, algebra, physics, and engineering. Understanding square roots is essential for solving quadratic equations, working with areas and volumes, and performing many types of calculations in science and engineering.
Let's explore the concept of square roots in more detail:
- The square root of a number x is a number y such that \( y^2 = x \).
- Square roots can be positive or negative since both \( y \) and \( -y \) satisfy the equation \( y^2 = x \).
- The principal square root is the non-negative root, denoted as √x.
For example, the principal square root of 225 is 15 because \( 15^2 = 225 \). Similarly, the negative square root of 225 is -15 because \( (-15)^2 = 225 \).
In general, to find the square root of a number:
- Identify the number you want to find the square root of.
- Determine if the number is a perfect square (a number whose square root is an integer).
- If the number is a perfect square, find the integer that, when multiplied by itself, equals the original number.
- If the number is not a perfect square, use approximation methods or a calculator to find the square root.
Understanding square roots also involves recognizing perfect squares. Perfect squares are numbers like 1, 4, 9, 16, 25, and 225, which have integer square roots. Knowing perfect squares can help quickly determine the square roots of these numbers.
Square roots are not limited to positive numbers. The square root of zero is zero, and the square roots of negative numbers are complex numbers, involving the imaginary unit i, where \( i = \sqrt{-1} \).
In summary, square roots are a fundamental concept in mathematics, providing a foundation for various mathematical operations and applications. Mastery of square roots enhances problem-solving skills and mathematical understanding.
What is the Square Root of 225?
The square root of 225 is 15. This means that when 15 is multiplied by itself, the result is 225. Mathematically, this can be expressed as:
\(\sqrt{225} = 15\)
Here are several methods to understand and calculate the square root of 225:
1. Prime Factorization Method
Prime factorization involves breaking down 225 into its prime factors:
- 225 = 3 × 3 × 5 × 5
- Grouping the prime factors in pairs: (3 × 3) and (5 × 5)
- Taking the square root of each pair: \(\sqrt{3^2} \times \sqrt{5^2} = 3 \times 5 = 15\)
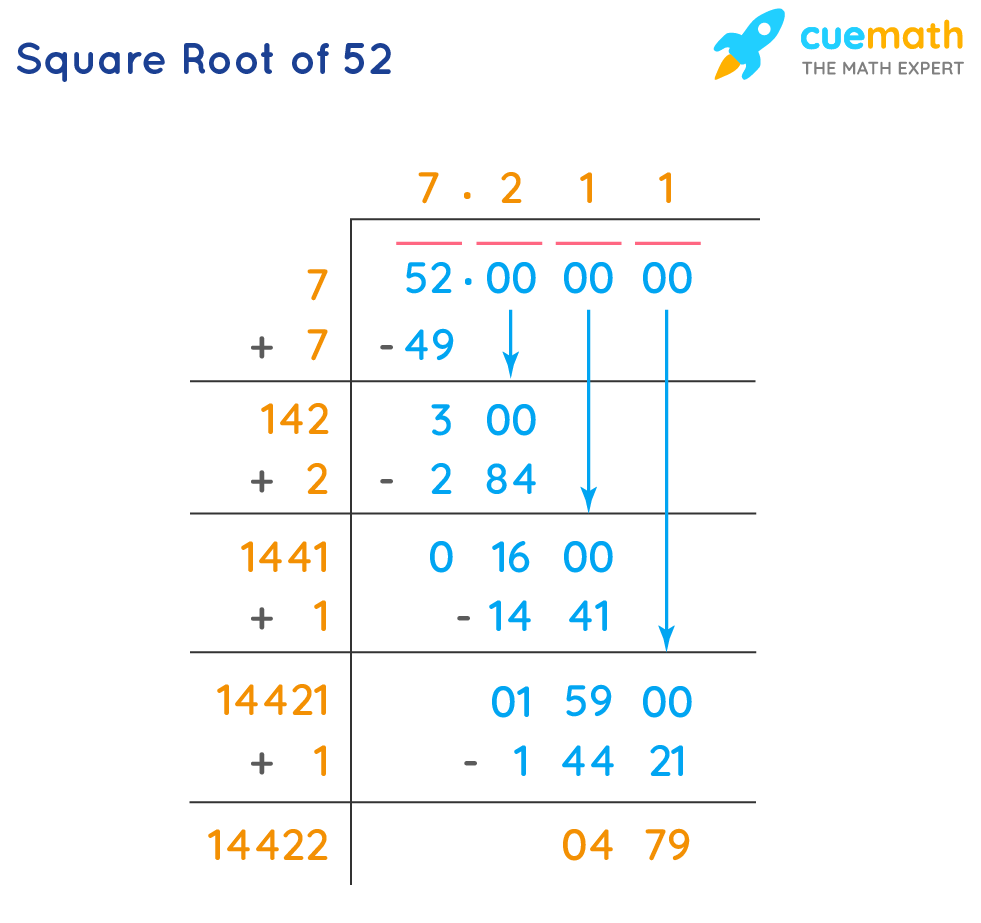
2. Long Division Method
The long division method is a step-by-step process:
- Write 225 under the division symbol and pair the digits starting from the right: (2)(25).
- Find the largest number whose square is less than or equal to the first pair (2). Here, it's 1 (since 1×1=1).
- Subtract the square (1) from the first pair (2), bring down the next pair (25) to make 125.
- Double the divisor (1 becomes 2), and find a number (5) that, when multiplied by the new divisor (25), gives 125.
- The quotient 15 is the square root of 225.
3. Repeated Subtraction Method
In the repeated subtraction method, you subtract successive odd numbers from 225 until you reach zero:
- 225 - 1 = 224
- 224 - 3 = 221
- 221 - 5 = 216
- 216 - 7 = 209
- 209 - 9 = 200
- 200 - 11 = 189
- 189 - 13 = 176
- 176 - 15 = 161
- 161 - 17 = 144
- 144 - 19 = 125
- 125 - 21 = 104
- 104 - 23 = 81
- 81 - 25 = 56
- 56 - 27 = 29
- 29 - 29 = 0
Thus, after 15 subtractions, you reach zero, confirming that the square root of 225 is 15.
4. Using a Calculator or Spreadsheet
To find the square root of 225 using a calculator, simply enter 225 and press the square root (√) button to get 15. In Excel or Google Sheets, use the formula:
=SQRT(225)
5. Exponential Form
In exponential form, the square root of 225 is written as:
\(225^{1/2} = 15\)
These methods demonstrate that the square root of 225 is indeed 15, which is a rational number and confirms that 225 is a perfect square.
Methods to Calculate the Square Root of 225
There are several methods to calculate the square root of 225, including prime factorization, the long division method, and estimation. Below, we will explain each method in detail.
Prime Factorization Method
The prime factorization method involves expressing 225 as a product of its prime factors.
- Step 1: Find the prime factors of 225. We start by dividing by the smallest prime number, which is 3.
225 ÷ 3 = 75 - Step 2: Continue factoring 75.
75 ÷ 3 = 25 - Step 3: Factor 25 by dividing by 5.
25 ÷ 5 = 5
5 ÷ 5 = 1
The prime factors of 225 are 3 × 3 × 5 × 5, which can be written as (3 × 5)². Hence, the square root of 225 is 3 × 5 = 15.
Long Division Method
The long division method provides a systematic way to find the square root of a number.
- Step 1: Write 225 under the long division symbol.
- Step 2: Pair the digits from the right. The pairs are 2 and 25.
- Step 3: Find the largest number whose square is less than or equal to 2. This is 1, because 1² = 1. Write 1 as the first digit of the quotient.
- Step 4: Subtract 1² from 2, bringing down the next pair of digits (25) to make 125.
- Step 5: Double the quotient (1) and find a digit (X) such that 2X × X is less than or equal to 125. This digit is 5 because 25 × 5 = 125.
- Step 6: Subtract 125 from 125 to get 0. The quotient is 15, which is the square root of 225.
Estimation Method
The estimation method involves finding two perfect squares between which 225 lies.
- Step 1: Identify the perfect squares closest to 225. These are 196 (14²) and 256 (16²).
- Step 2: Since 225 is closer to 256, estimate the square root to be closer to 15.
By refining the estimate, we confirm that the square root of 225 is 15.
All these methods demonstrate that the square root of 225 is indeed 15.
Understanding Perfect Squares
A perfect square is an integer that is the square of another integer. In other words, a number is a perfect square if it can be expressed as the product of an integer with itself. For example, 225 is a perfect square because it equals 15 × 15.
Here are some key properties and examples of perfect squares:
- Definition: A perfect square is a number that can be written as \( n^2 \) where \( n \) is an integer.
- Examples: Some examples of perfect squares include 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, and 225.
- Square Roots: The square root of a perfect square is always an integer. For instance, the square root of 225 is 15.
Perfect squares have unique properties that make them easily identifiable:
- They always end in specific digits: If a number ends in 1, 4, 5, 6, or 9, it could be a perfect square.
- They are always non-negative: Since squaring any real number (positive or negative) results in a non-negative product, perfect squares are always non-negative.
- They have an odd number of total factors: Perfect squares have an odd number of total factors because one of the factors is repeated (the square root).
One interesting way to identify a perfect square is through its visual representation. Consider arranging objects into a square grid. If they form a complete square, the total number of objects is a perfect square. For example, arranging 225 objects into a 15 by 15 grid confirms that 225 is a perfect square.
Methods to Determine Perfect Squares
To determine if a number is a perfect square, you can use the following methods:
- Prime Factorization: Break down the number into its prime factors. If all prime factors appear an even number of times, the number is a perfect square. For example, the prime factorization of 225 is \( 3^2 \times 5^2 \).
- Square Root Test: Calculate the square root of the number. If the result is an integer, then the number is a perfect square. For instance, \( \sqrt{225} = 15 \).
- Digit Patterns: Recognize patterns in the last digit of perfect squares. For example, perfect squares can end in 1, 4, 5, 6, or 9, but not in 2, 3, 7, or 8.
Perfect squares are fundamental in various mathematical applications and problem-solving scenarios. They appear frequently in geometry, algebra, and number theory, providing a foundation for understanding more complex mathematical concepts.
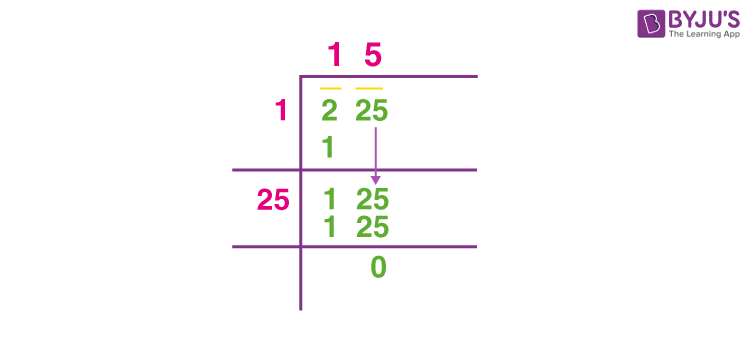
Applications of the Square Root of 225
The square root of 225, which is 15, finds various applications across different fields, demonstrating its practical utility in both theoretical and real-world scenarios. Here are some key applications:
-
Geometry and Architecture:
In geometry and architectural design, calculating the dimensions of squares and rectangular structures is essential. Knowing that the square root of 225 is 15 helps architects and engineers determine the side length of a square area that is 225 square units, ensuring accurate and efficient space planning.
-
Physics:
Square roots are crucial in physics, especially when dealing with formulas involving vectors, velocity, and force. For example, if the resultant force acting on an object has a squared magnitude of 225 newton squared, its actual magnitude is 15 newtons.
-
Statistics:
In statistics, the square root function is used to calculate standard deviation, which measures the variability or dispersion of a set of data points. For a data set with a variance of 225, the standard deviation would be 15, helping analysts understand the spread of the data.
-
Finance:
Square roots are applied in financial models to determine the volatility of assets. For instance, the Black-Scholes model, used for pricing options, involves the square root function to assess market fluctuations and risks accurately.
-
Computer Graphics:
In computer graphics, algorithms often use square roots to calculate distances between points in a 3D space. This is essential for rendering realistic lighting, shadows, and textures, enhancing the visual appeal of digital images and animations.
-
Education:
The concept of square roots, exemplified by the square root of 225, is a fundamental part of mathematics education. It helps students develop numerical and algebraic skills, fostering a deeper understanding of mathematical principles.
-
Engineering:
In engineering, square roots are used in various calculations, such as determining the load distribution on structures, the dimensions of components, and in stress analysis. Understanding the square root of 225 can aid in designing and testing prototypes effectively.
These applications illustrate how the square root of 225 is not just a theoretical number but a practical tool that aids in solving a wide array of problems across multiple disciplines.
Square Root Function in Mathematics
The square root function is a fundamental mathematical function denoted as \( f(x) = \sqrt{x} \). It is defined for all non-negative real numbers and maps each number to its principal (non-negative) square root.
Properties of the Square Root Function
- Domain: The function is defined for all \( x \geq 0 \), i.e., the domain is \([0, \infty)\).
- Range: The range of the function is also \([0, \infty)\), since square roots of non-negative numbers are non-negative.
- Intercepts: The function has a single intercept at the origin \((0,0)\).
- Monotonicity: The square root function is strictly increasing on its entire domain. This means that as \( x \) increases, \( \sqrt{x} \) also increases.
- One-to-One Function: The function is one-to-one, meaning each output value corresponds to exactly one input value.
Graph of the Square Root Function
The graph of the square root function \( f(x) = \sqrt{x} \) is a curve that starts at the origin and increases gradually, becoming less steep as \( x \) increases. Below is an example graph:

Transformations of the Square Root Function
Transformations can be applied to the basic square root function to shift, stretch, or compress its graph. These transformations include:
- Vertical Shifts: \( f(x) = \sqrt{x} + d \) shifts the graph vertically by \( d \) units.
- Horizontal Shifts: \( f(x) = \sqrt{x - c} \) shifts the graph horizontally by \( c \) units.
- Vertical Stretch/Compression: \( f(x) = a\sqrt{x} \) stretches the graph vertically if \( |a| > 1 \) and compresses it if \( |a| < 1 \).
- Reflections: \( f(x) = -\sqrt{x} \) reflects the graph across the x-axis.
Examples of Square Root Function
| Expression | Transformation |
|---|---|
| \( f(x) = \sqrt{x} \) | Basic square root function |
| \( f(x) = \sqrt{x} + 3 \) | Vertical shift up by 3 units |
| \( f(x) = \sqrt{x - 2} \) | Horizontal shift right by 2 units |
| \( f(x) = 2\sqrt{x} \) | Vertical stretch by a factor of 2 |
| \( f(x) = -\sqrt{x} \) | Reflection across the x-axis |
Common Mistakes and Misconceptions
- It is incorrect to write \( \sqrt{25} = \pm 5 \). The square root function \( \sqrt{x} \) always returns the principal (positive) square root, so \( \sqrt{25} = 5 \).
- The expression \( \sqrt{x^2} = x \) is only true for non-negative \( x \). Generally, \( \sqrt{x^2} = |x| \) to account for both positive and negative values of \( x \).
Applications of the Square Root Function
Square root functions are used in various fields such as physics, engineering, and finance. They are essential in solving quadratic equations, calculating distances, and modeling natural phenomena.
Historical Context of Square Roots
The concept of square roots dates back to ancient civilizations and has a rich history in the development of mathematics.
Ancient Civilizations: The Babylonians, as early as 2000 BCE, were known to have methods for approximating square roots. Clay tablets from that era show their understanding and use of square root calculations.
Greek Contributions: The Greeks made significant advancements in the study of square roots. Pythagoras and his followers explored the properties of square numbers and roots, particularly through the famous Pythagorean Theorem. Euclid, in his work "Elements," formalized many properties of square roots.
Indian Mathematics: In ancient India, mathematicians like Aryabhata and Brahmagupta made substantial contributions to the understanding of square roots. They developed algorithms to compute square roots and wrote extensively about their properties.
Islamic Golden Age: During the Islamic Golden Age, mathematicians such as Al-Khwarizmi further advanced the methods for calculating square roots. His work influenced both the development of algebra and the techniques used in Europe later on.
Renaissance and Modern Era: In the Renaissance, European mathematicians like Fibonacci brought Arabic mathematical knowledge to Europe. The notation for square roots evolved, and the understanding deepened with the advent of algebra. Modern computational methods and the advent of computers have made calculating square roots an essential aspect of various scientific fields.
Understanding the historical context of square roots provides insight into how mathematical concepts evolve over time and the contributions of various cultures to the field of mathematics.
Common Mistakes and Misconceptions
Understanding and correctly working with square roots is essential in mathematics. However, there are several common mistakes and misconceptions that students often encounter when dealing with square roots, particularly with numbers like 225. Here are some of the most frequent errors and how to avoid them:
-
Incorrect Simplification:
Students sometimes incorrectly simplify the square root of a number. For example, they might think that \(\sqrt{225} = 22.5\) instead of \(\sqrt{225} = 15\). The correct simplification involves recognizing that 225 is a perfect square and finding the integer value.
-
Forgetting to Consider Both Positive and Negative Roots:
When solving equations that involve square roots, it’s important to remember that both positive and negative roots should be considered. For instance, \(x^2 = 225\) has solutions \(x = 15\) and \(x = -15\). Neglecting the negative root is a common oversight.
-
Misapplying the Order of Operations:
Students might incorrectly apply the order of operations (PEMDAS/BODMAS) when working with square roots. For example, in the expression \(\sqrt{3^2 + 4^2}\), they might mistakenly calculate \(\sqrt{3^2} + 4^2\), leading to incorrect results.
-
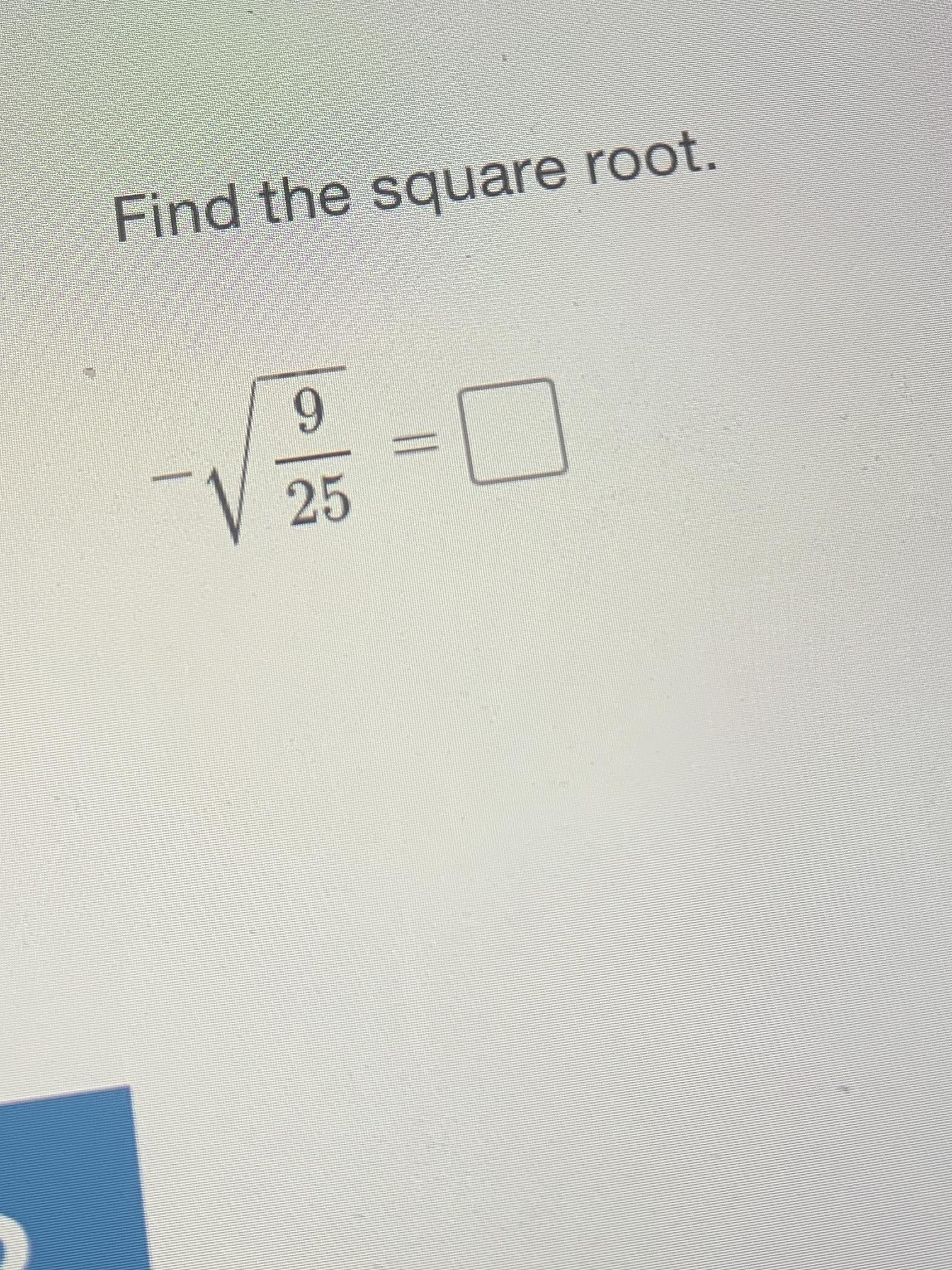
Confusing Square Roots with Division:
Some students confuse the square root symbol with division, particularly when it appears in complex expressions. For example, \(\sqrt{25/4}\) should be simplified as \(\sqrt{25}/\sqrt{4} = 5/2\), not as \(\sqrt{6.25}\).
-
Misunderstanding the Properties of Square Roots:
Misunderstanding properties such as \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\) can lead to errors. For example, assuming \(\sqrt{225 \times 4} = \sqrt{225} \times \sqrt{4}\) without proper simplification might cause confusion.
-
Ignoring the Principal Square Root:
In some contexts, students might not realize that the principal square root (the non-negative root) is usually what is referred to when using the square root symbol. For example, \(\sqrt{225}\) conventionally refers to 15, not -15.
-
Errors in Calculating Square Roots of Large Numbers:
When dealing with large numbers, manual errors can occur. Using a calculator correctly and double-checking calculations is crucial. For example, estimating \(\sqrt{225}\) without a calculator might lead to approximations, but recognizing 225 as a perfect square helps in finding the exact value.
-
Misapplication of Properties in Algebraic Contexts:
Errors often occur when students apply properties of square roots in algebraic expressions. For instance, in simplifying expressions like \(\sqrt{(x+2)^2}\), students might overlook that \(\sqrt{(x+2)^2} = |x+2|\) and not just \(x+2\).
By being aware of these common mistakes and misconceptions, students can improve their understanding and accuracy when working with square roots.

Practice Problems and Solutions
Here are some practice problems along with their solutions to help you understand how to calculate square roots, specifically focusing on the square root of 225:
- Problem 1: Find the square root of 225.
- Solution:
The square root of 225 is calculated as follows:
\[\sqrt{225} = 15\]
- Solution:
- Problem 2: If the area of a square is 225 square units, find the length of one side.
- Solution:
The length of one side is the square root of the area.
\[\text{Side length} = \sqrt{225} = 15 \text{ units}\]
- Solution:
- Problem 3: Calculate the square root of 225 by the long division method.
- Solution:
Step-by-step long division method:
Step 1:
Group the digits in pairs from right to left: 2|25.
Step 2:
Find the largest number whose square is less than or equal to the first group (2). This number is 1 (since \(1^2 = 1\)).
Step 3:
Subtract 1 from 2, get 1. Bring down the next pair of digits (25), making it 125.
Step 4:
Double the divisor (1), get 2. Determine the largest digit (x) such that 2x * x ≤ 125. Here, x = 5 (since \(25 * 5 = 125\)).
Step 5:
Thus, the quotient is 15 and the remainder is 0.
Conclusion:
\(\sqrt{225} = 15\)
- Solution:
- Problem 4: A square has a perimeter of 60 units. Find the area of the square.
- Solution:
The perimeter of a square is 4 times the side length. Let s be the side length.
\[4s = 60\]
\[s = 15\]
The area of the square is \(s^2\).
\[\text{Area} = 15^2 = 225 \text{ square units}\]
- Solution:
These problems demonstrate the use of the square root of 225 in different mathematical contexts.
Video hướng dẫn cách tìm căn bậc hai của 225 bằng phương pháp phân tích thừa số nguyên tố. Tìm hiểu về căn bậc hai của 225 và áp dụng nó trong toán học.
Cách Tìm Căn Bậc Hai của 225 bằng Phân Tích Thừa Số Nguyên Tố / Căn Bậc Hai của 225 / 225 Căn Bậc Hai
READ MORE:
Tìm căn bậc hai của 225, 256, 20 và căn bậc hai của 40 không dùng máy tính