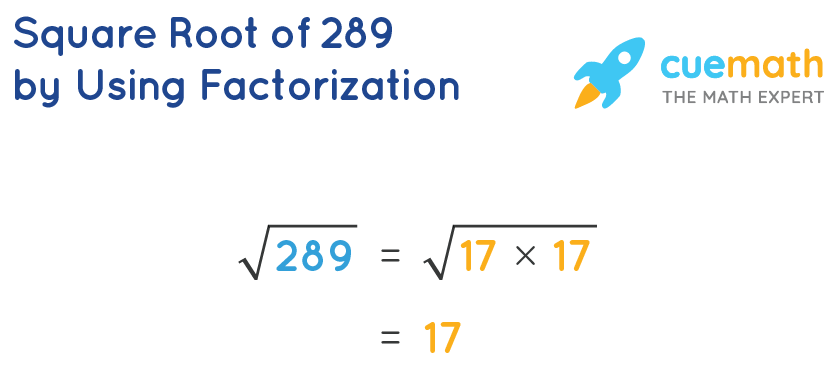Topic what's the square root of 25: What's the square root of 25? In this article, we'll explore the simple yet fascinating answer to this question, delve into the concept of square roots, and understand their significance in mathematics. Join us as we uncover the mathematical beauty behind the square root of 25 and its applications.
Table of Content
- Square Root of 25
- Introduction to Square Roots
- Understanding the Square Root of 25
- Mathematical Definition
- Calculation of the Square Root of 25
- Properties of Square Roots
- Positive and Negative Square Roots
- Perfect Squares
- Visualizing the Square Root
- Square Roots in Geometry
- Applications of Square Roots
- Square Roots in Algebra
- Square Roots in Real-Life Situations
- Frequently Asked Questions about Square Roots
- YOUTUBE: Khám phá căn bậc hai của 25 qua video hấp dẫn này. Tìm hiểu cách tính và ứng dụng của căn bậc hai trong toán học và đời sống hàng ngày.
Square Root of 25
The square root of 25 is a fundamental mathematical concept. It is the number which, when multiplied by itself, gives the product 25. The square root is denoted by the radical symbol √.
Calculation
Mathematically, the square root of 25 is represented as:
\[
\sqrt{25} = 5
\]
This is because:
\[
5 \times 5 = 25
\]
Explanation
The square root of a number \( n \) is a value that, when multiplied by itself, equals \( n \). In the case of 25, 5 is the number that satisfies this condition. Thus, we say:
\[
\sqrt{25} = 5
\]
Properties of the Square Root of 25
- Positive and Negative Roots: The principal square root of 25 is 5. However, -5 is also a square root of 25 because:
Although -5 is a valid square root, the principal (or non-negative) square root is typically considered to be the primary value.
\[
(-5) \times (-5) = 25
\] - Perfect Square: 25 is a perfect square, meaning it is the product of an integer multiplied by itself. In this case:
\[
5 \times 5 = 25
\]
Visual Representation
To visualize the square root of 25, imagine a square with an area of 25 square units. Each side of this square would measure 5 units, as the area of a square is calculated by squaring the length of one of its sides:
\[
\text{Area} = \text{side} \times \text{side} = 5 \times 5 = 25
\]
Therefore, the length of each side of the square is the square root of the area, which is 5 units.
Conclusion
Understanding the square root of 25 helps in grasping broader mathematical concepts related to roots and exponents. The square root function is fundamental in algebra, geometry, and various fields of science and engineering.

READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics, representing a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is a number that, when multiplied by itself, equals 25.
The square root symbol is denoted as √. Mathematically, this is represented as:
\[
\sqrt{n}
\]
where \( n \) is the number for which we are finding the square root.
Let's break down the concept step by step:
- Understanding Multiplication: To grasp square roots, one must first understand multiplication. For instance, \( 5 \times 5 = 25 \).
- Definition of Square Roots: The square root of a number \( n \) is a value \( x \) such that \( x \times x = n \). In this case, \( 5 \times 5 = 25 \), so \( \sqrt{25} = 5 \).
- Positive and Negative Roots: While the principal square root is typically positive, every positive number actually has two square roots: one positive and one negative. Therefore, \( \sqrt{25} = 5 \) and \( \sqrt{25} = -5 \).
Square roots are not limited to whole numbers. They can also be fractions or irrational numbers, which cannot be expressed as a simple fraction. For instance, the square root of 2 is an irrational number.
Understanding square roots is essential for solving various mathematical problems and is widely used in algebra, geometry, physics, engineering, and many other fields.
Here is a table summarizing some common square roots:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
Understanding the Square Root of 25
The square root of 25 is a straightforward concept in mathematics, but it holds significant importance. It represents a number which, when multiplied by itself, results in 25. This concept is fundamental for understanding more complex mathematical ideas.
Here’s a detailed explanation of how we find the square root of 25:
- Definition: The square root of a number \( n \) is a value \( x \) such that \( x \times x = n \). For 25, we are looking for a number \( x \) that satisfies \( x \times x = 25 \).
- Simple Calculation: By examining the multiplication of integers, we find that:
Thus, \( 5 \) is the square root of \( 25 \).
\[
5 \times 5 = 25
\] - Principal Square Root: The principal (or non-negative) square root of 25 is 5, denoted as:
\[
\sqrt{25} = 5
\] - Negative Square Root: It’s important to note that -5 is also a square root of 25 because:
However, when we refer to "the square root," we typically mean the principal square root, which is positive.
\[
(-5) \times (-5) = 25
\] - Perfect Squares: 25 is known as a perfect square because it is the product of an integer multiplied by itself. In this case:
\[
5 \times 5 = 25
\]
Understanding that the square root of 25 is 5 helps in various mathematical applications, from solving quadratic equations to understanding geometric principles. It forms the basis for more advanced topics in algebra and calculus.
Here's a quick reference table for some perfect squares and their square roots:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
Mathematical Definition
The square root of a number is a value that, when multiplied by itself, gives the original number. This concept is fundamental in mathematics and is used extensively in various fields such as algebra, geometry, and calculus.
Let's break down the mathematical definition of the square root of 25:
- Square Root Symbol: The square root is denoted by the radical symbol \( \sqrt{} \). For the number 25, it is written as:
\[
\sqrt{25}
\] - Basic Definition: The square root of 25 is the number that, when multiplied by itself, equals 25. This can be expressed mathematically as:
Where \( x \) is the square root of 25.
\[
x^2 = 25
\] - Solving for \( x \): To find the value of \( x \), we determine which number squared equals 25. Through simple calculation:
Thus, \( x = 5 \).
\[
5 \times 5 = 25
\] - Principal Square Root: The principal (or non-negative) square root of 25 is 5, represented as:
\[
\sqrt{25} = 5
\] - Negative Square Root: It is also important to acknowledge the negative square root. Since:
-5 is also a square root of 25. However, the principal square root is typically the positive value.
\[
(-5) \times (-5) = 25
\]
The concept of square roots extends beyond just integers. It includes fractions and irrational numbers as well. For example, the square root of 2 is an irrational number that cannot be expressed as a simple fraction.
Here is a summary table of the square roots of some common numbers:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
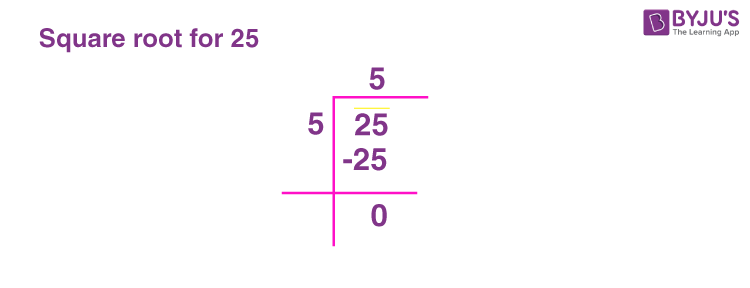
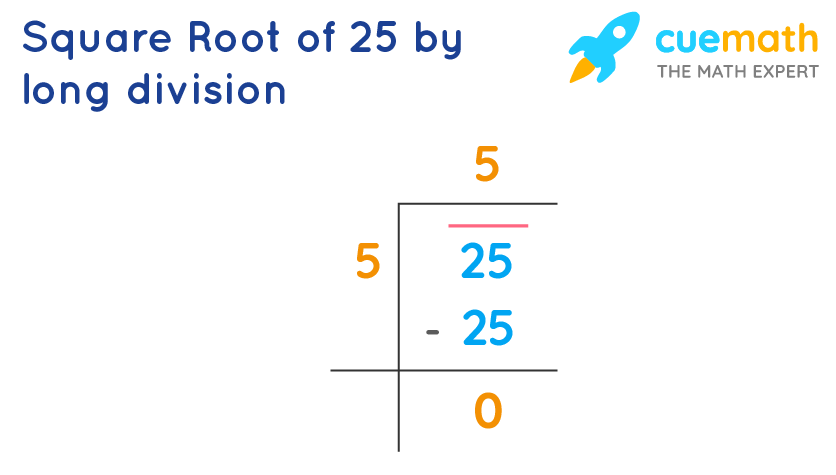
Calculation of the Square Root of 25
Calculating the square root of 25 is a straightforward process, as it involves finding a number that, when multiplied by itself, equals 25. Here’s a detailed step-by-step explanation:
- Identify the Problem: We need to find the value of \( x \) such that:
\[
x^2 = 25
\] - Initial Assumptions: Consider potential values for \( x \). We know that:
Therefore, \( x = 5 \) is a candidate.
\[
5 \times 5 = 25
\] - Verification: Verify that the candidate value satisfies the original equation:
The equation holds true, confirming that \( x = 5 \) is correct.
\[
5^2 = 25
\] - Principal Square Root: The principal (or positive) square root of 25 is:
\[
\sqrt{25} = 5
\] - Negative Square Root: Additionally, consider the negative square root:
Thus, \( -5 \) is also a square root of 25, although the principal square root is the positive value.
\[
(-5)^2 = 25
\]
In summary, the calculation shows that the square root of 25 is both 5 and -5, with 5 being the principal square root. This understanding is crucial for various mathematical applications, from basic algebra to more complex problem-solving.
Here is a table for quick reference of some perfect squares and their square roots:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |

Properties of Square Roots
Square roots have several important properties that make them a fundamental concept in mathematics. These properties help in simplifying expressions and solving equations involving square roots.
- Non-Negative Result: The principal square root of a non-negative number is always non-negative. For example:
\[
\sqrt{25} = 5
\] - Product Property: The square root of a product is the product of the square roots of the factors. Mathematically:
For example:
\[
\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}
\]
\[
\sqrt{36 \cdot 25} = \sqrt{36} \cdot \sqrt{25} = 6 \cdot 5 = 30
\] - Quotient Property: The square root of a quotient is the quotient of the square roots of the numerator and the denominator. This can be expressed as:
For instance:
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
\[
\sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2} = 2.5
\] - Square of a Square Root: The square of a square root returns the original number:
For example:
\[
(\sqrt{a})^2 = a
\]
\[
(\sqrt{25})^2 = 25
\] - Even and Odd Roots: The square root of an even power of a number results in an even power, and the square root of an odd power is not an integer. For example:
\[
\sqrt{16} = 4 \quad \text{and} \quad \sqrt{81} = 9
\] - Irrational Numbers: The square roots of non-perfect squares are irrational numbers. They cannot be expressed as exact fractions. For example:
\[
\sqrt{2} \approx 1.414
\]
Understanding these properties of square roots aids in simplifying complex mathematical expressions and solving various types of equations. They are essential tools in algebra, geometry, calculus, and other areas of mathematics.
Here is a table summarizing the square roots of some common numbers:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
| 36 | 6 |
| 49 | 7 |
| 64 | 8 |
| 81 | 9 |
| 100 | 10 |
Positive and Negative Square Roots
Square roots can be both positive and negative. This is because squaring either a positive or a negative number yields a positive result. Understanding the concept of positive and negative square roots is crucial for solving various mathematical problems.
- Positive Square Root: The principal square root of a number is its positive square root. For example:
This is because \( 5 \times 5 = 25 \).
\[
\sqrt{25} = 5
\] - Negative Square Root: The negative square root of a number is simply the negative of its principal square root. For example:
This is because \( (-5) \times (-5) = 25 \).
\[
\sqrt{25} = -5
\] - General Form: Any positive number \( n \) has two square roots: one positive and one negative. This can be expressed as:
For 25, it can be written as:
\[
\sqrt{n} = \pm \sqrt{n}
\]
\[
\sqrt{25} = \pm 5
\] - Application in Equations: When solving quadratic equations, both the positive and negative square roots are considered. For example, solving the equation \( x^2 = 25 \) involves finding both:
\[
x = 5 \quad \text{and} \quad x = -5
\]
To summarize, the square root of 25 includes both +5 and -5. Understanding both positive and negative square roots is essential for comprehensive problem-solving in mathematics.
Here’s a table showing the positive and negative square roots of some common numbers:
| Number | Positive Square Root | Negative Square Root |
|---|---|---|
| 1 | 1 | -1 |
| 4 | 2 | -2 |
| 9 | 3 | -3 |
| 16 | 4 | -4 |
| 25 | 5 | -5 |
| 36 | 6 | -6 |
| 49 | 7 | -7 |
| 64 | 8 | -8 |
| 81 | 9 | -9 |
| 100 | 10 | -10 |
Perfect Squares
Perfect squares are integers that are the square of other integers. In other words, a perfect square is a number that can be expressed as the product of an integer with itself. Understanding perfect squares is fundamental in various branches of mathematics, including algebra and number theory.
Here’s a detailed explanation of perfect squares:
- Definition: A perfect square is a number that can be written as \( n^2 \), where \( n \) is an integer. For example:
This indicates that 25 is a perfect square.
\[
25 = 5^2
\] - Properties of Perfect Squares: Perfect squares have unique properties that make them easily recognizable:
- They always end in 0, 1, 4, 5, 6, or 9 in the decimal system.
- The number of zeros at the end of a perfect square is always even.
- They are always non-negative, as squaring any real number (positive or negative) results in a non-negative product.
- Identifying Perfect Squares: To determine if a number is a perfect square, find its square root and check if the result is an integer. For instance:
Since 5 is an integer, 25 is a perfect square.
\[
\sqrt{25} = 5
\] - Examples of Perfect Squares: Here are some common perfect squares:
- \( 1 = 1^2 \)
- \( 4 = 2^2 \)
- \( 9 = 3^2 \)
- \( 16 = 4^2 \)
- \( 25 = 5^2 \)
- \( 36 = 6^2 \)
- \( 49 = 7^2 \)
- \( 64 = 8^2 \)
- \( 81 = 9^2 \)
- \( 100 = 10^2 \)
- Applications: Perfect squares are used in various mathematical problems and real-life applications:
- Geometry: Calculating the area of squares.
- Algebra: Solving quadratic equations.
- Number theory: Analyzing properties of integers.
Below is a table summarizing the perfect squares from 1 to 100:
| Number | Perfect Square |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
Visualizing the Square Root
Visualizing the square root of a number helps in understanding its value and significance better. In this section, we will focus on how to visualize the square root of 25 using different methods and tools.
Graphical Representation
One effective way to visualize the square root of 25 is through a graphical representation on a number line.
- Mark 0 at the start of the number line.
- Mark 25 further along the number line.
- The square root of 25 is the number which, when multiplied by itself, equals 25. This number is 5.
- Locate 5 on the number line. This is the square root of 25.

Area Model
Another way to visualize the square root of 25 is by using an area model.
- Draw a square with an area of 25 square units.
- Since the area of a square is given by \( \text{side}^2 \), we find that each side of this square is 5 units long.
- This visual representation helps to understand that the square root of 25 is the length of each side of the square.

Geometric Interpretation
In geometry, the square root of a number can be visualized by the length of the side of a square with a given area.
- Imagine a square with a total area of 25 square units.
- The length of each side of this square is the square root of the total area.
- Therefore, each side of the square is 5 units long.
This geometric interpretation solidifies the understanding that the square root of 25 is 5.
Using MathJax for Precise Representation
We can use MathJax to present the mathematical expression and its visual understanding.
For example, the square root of 25 is represented as:
\(\sqrt{25} = 5\)
This equation confirms that 5 multiplied by itself equals 25:
\(5 \times 5 = 25\)
Square Roots in Geometry
The concept of square roots is deeply integrated into geometry, particularly when dealing with areas and distances. To understand how the square root of 25 fits into geometric contexts, let's explore some key points:
1. Area of a Square:
The most straightforward geometric interpretation of the square root is related to the area of a square. If a square has an area of 25 square units, the length of each side is the square root of the area.
- Area = \( s^2 \) where \( s \) is the side length.
- \( 25 = s^2 \)
- \( s = \sqrt{25} = 5 \)
This means a square with an area of 25 square units has sides that are 5 units long.
2. Distance in Coordinate Geometry:
Square roots are also crucial in calculating distances between points in coordinate geometry. The distance formula between two points \((x_1, y_1)\) and \((x_2, y_2)\) is:
\[
d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
For example, the distance between points \((0, 0)\) and \((3, 4)\) can be calculated as:
- \[ d = \sqrt{(3 - 0)^2 + (4 - 0)^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \]
3. Pythagorean Theorem:
The square root also appears in the Pythagorean theorem, which relates the sides of a right triangle. For a right triangle with legs of lengths \(a\) and \(b\), and hypotenuse \(c\), the theorem states:
\[
a^2 + b^2 = c^2
\]
If \(a = 3\) and \(b = 4\):
- \[ c^2 = 3^2 + 4^2 = 9 + 16 = 25 \]
- \[ c = \sqrt{25} = 5 \]
4. Visual Representation on a Grid:
Visualizing square roots can be done on a coordinate grid. For instance, a 5x5 grid represents the number 25, and the length of each side is the square root of 25, which is 5.
Here is a simple grid to visualize:
| • | • | • | • | • |
| • | • | • | • | • |
| • | • | • | • | • |
| • | • | • | • | • |
| • | • | • | • | • |
Each dot represents one unit, and the entire 5x5 grid represents the area of 25 square units.
In conclusion, the square root of 25, which is 5, plays a significant role in various geometric contexts such as areas, distances, and the Pythagorean theorem. Understanding these applications helps in visualizing and comprehending the geometric significance of square roots.
Applications of Square Roots
Square roots are used in various fields and applications. Here are some of the key areas where square roots play a crucial role:
-
Geometry:
In geometry, square roots are used to calculate distances and lengths. For example, in the Pythagorean theorem, the length of the hypotenuse \(c\) of a right triangle is found using the formula:
\[
c = \sqrt{a^2 + b^2}
\]
where \(a\) and \(b\) are the lengths of the other two sides. -
Algebra:
Square roots are often used in algebra to solve quadratic equations. The solutions to the equation \(ax^2 + bx + c = 0\) are given by the quadratic formula:
\[
x = \frac{{-b \pm \sqrt{b^2 - 4ac}}}{2a}
\] -
Physics:
In physics, square roots are used in formulas for calculating energy, force, and velocity. For example, the formula for the period \(T\) of a simple pendulum is:
\[
T = 2\pi \sqrt{\frac{L}{g}}
\]
where \(L\) is the length of the pendulum and \(g\) is the acceleration due to gravity. -
Engineering:
Engineers use square roots in various calculations, such as determining the stress and strain on materials, analyzing electrical circuits, and optimizing design parameters. For instance, the root mean square (RMS) value of an alternating current (AC) is given by:
\[
I_{RMS} = \sqrt{\frac{1}{T} \int_0^T [i(t)]^2 \, dt}
\]
where \(i(t)\) is the instantaneous current and \(T\) is the period. -
Statistics:
In statistics, the standard deviation, which measures the amount of variation or dispersion in a set of values, involves the square root of the variance:
\[
\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2}
\]
where \(N\) is the number of observations, \(x_i\) are the individual values, and \(\mu\) is the mean. -
Computer Graphics:
Square roots are used in computer graphics to calculate distances between points in 2D and 3D space, which is crucial for rendering images and animations. The distance \(D\) between two points \((x_1, y_1)\) and \((x_2, y_2)\) in 2D is given by:
\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}
\]
and in 3D, the distance formula extends to:\[
D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}
\]
where \((z_1, z_2)\) are the z-coordinates of the points.
Square roots are essential tools in many scientific, engineering, and mathematical applications, facilitating the solving of complex problems and contributing to advancements in technology and understanding of the natural world.
Square Roots in Algebra
Square roots play a fundamental role in algebra, particularly in solving equations and understanding functions. The square root of a number \( x \) is a value that, when multiplied by itself, gives \( x \). This can be expressed mathematically as:
\[ \sqrt{x} = y \text{ such that } y^2 = x \]
In algebra, square roots are used to solve quadratic equations. A quadratic equation is any equation that can be rearranged into the form:
\[ ax^2 + bx + c = 0 \]
where \( a \), \( b \), and \( c \) are constants. To solve such equations, one method is to use the quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Here, the term under the square root, \( b^2 - 4ac \), is called the discriminant. The discriminant determines the nature of the roots of the quadratic equation:
- If \( b^2 - 4ac > 0 \), the equation has two distinct real roots.
- If \( b^2 - 4ac = 0 \), the equation has exactly one real root (a repeated root).
- If \( b^2 - 4ac < 0 \), the equation has two complex roots.
Square roots are also essential in defining and understanding the properties of different functions. For example, the function:
\[ f(x) = \sqrt{x} \]
is defined for all non-negative \( x \) and represents the principal (positive) square root of \( x \). In more advanced algebra, square roots are used in solving systems of equations, particularly when dealing with nonlinear systems.
Another important application of square roots in algebra is simplifying expressions involving radicals. For instance, to simplify the expression \( \sqrt{50} \), you can factor it into prime factors:
\[ \sqrt{50} = \sqrt{25 \times 2} = \sqrt{25} \times \sqrt{2} = 5\sqrt{2} \]
This process of simplification helps in solving equations and in performing arithmetic operations with square roots.
In summary, square roots are a crucial concept in algebra, aiding in solving quadratic equations, simplifying radical expressions, and understanding various algebraic functions and their properties.
Square Roots in Real-Life Situations
Square roots have numerous applications in real-life situations across various fields. Here are some key areas where square roots play a vital role:
- Engineering and Architecture:
Square roots are used extensively in engineering and architecture. For example, when determining the length of the hypotenuse in a right triangle, the Pythagorean theorem (\(a^2 + b^2 = c^2\)) is often applied. This theorem helps in designing structures and solving problems related to distances.
- Finance:
In finance, square roots are used to calculate the rate of return on investments over a period of time. The formula \( R = \sqrt{\frac{V_2}{V_0}} - 1 \) is used, where \( V_0 \) is the initial value and \( V_2 \) is the value after two periods.
- Probability and Statistics:
Square roots are crucial in probability and statistics, particularly in the calculation of standard deviation and variance. These measures are used to understand the spread and dispersion of data in a dataset. The formula for standard deviation is \( \sigma = \sqrt{\frac{1}{N} \sum_{i=1}^N (x_i - \mu)^2} \), where \( N \) is the number of data points, \( x_i \) is each individual data point, and \( \mu \) is the mean of the data points.
- Physics:
In physics, square roots are often used in formulas that describe natural phenomena. For instance, the formula for the period of a pendulum is \( T = 2\pi \sqrt{\frac{L}{g}} \), where \( T \) is the period, \( L \) is the length of the pendulum, and \( g \) is the acceleration due to gravity.
- Carpentry and Construction:
Carpenters and construction workers use square roots to calculate measurements and ensure precision in their work. For example, when cutting materials to fit into right-angled spaces, the Pythagorean theorem helps in determining the correct lengths.
- Graphics and Design:
In graphic design and computer graphics, square roots are used to calculate distances between points, which is essential for rendering images and animations. The distance formula \( D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \) is commonly used for this purpose.
Overall, square roots are fundamental in various practical applications, aiding in calculations and problem-solving across different domains.
Frequently Asked Questions about Square Roots
-
What is a square root?
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5, because \(5 \times 5 = 25\).
-
What are the square roots of 25?
The number 25 has two square roots: \(+5\) and \(-5\). This is because both \((5)^2\) and \((-5)^2\) equal 25.
-
Why are there both positive and negative square roots?
Every positive number has two square roots: one positive and one negative. This is because both a positive number and its negative counterpart, when squared, yield the same positive result. For example, \(5^2 = 25\) and \((-5)^2 = 25\).
-
What is the principal square root?
The principal square root is the non-negative square root of a number. For example, the principal square root of 25 is 5.
-
Can negative numbers have real square roots?
No, negative numbers do not have real square roots because no real number squared equals a negative number. However, they do have complex square roots. For instance, the square root of \(-25\) is \(5i\), where \(i\) is the imaginary unit, satisfying \(i^2 = -1\).
-
What are some common methods to find square roots?
Square roots can be found using various methods, such as:
- Prime factorization
- Using a calculator
- Estimating and refining guesses
- Using the long division method
-
What is the square root of a perfect square?A perfect square is a number that is the square of an integer. For example, 25 is a perfect square because it is \(5^2\). The square root of a perfect square is always an integer.
-
How are square roots used in real life?
Square roots have various applications in real life, including in geometry (calculating the side length of a square), physics (solving quadratic equations), and computer graphics (distance calculations).
-
What is the square root symbol and how is it used?
The square root symbol is \(\sqrt{}\). To find the square root of a number \(n\), you write it as \(\sqrt{n}\). For example, \(\sqrt{25} = 5\).
Khám phá căn bậc hai của 25 qua video hấp dẫn này. Tìm hiểu cách tính và ứng dụng của căn bậc hai trong toán học và đời sống hàng ngày.
Căn bậc hai của 25 - Hướng dẫn chi tiết
READ MORE:
Video giải thích tại sao căn bậc hai của 25 là 5 và làm thế nào để hiểu đúng về khái niệm này. Khám phá thêm về toán học và các ứng dụng thực tế của căn bậc hai.
Căn bậc hai của 25 là bao nhiêu? Hầu hết không hiểu tại sao họ có câu trả lời ĐÚNG!