Square Root of 200 in Radical Form: Simplified Explanation and Guide

The square root of 200 can be expressed in its simplest radical form. To simplify the square root of 200, we need to find the prime factorization of 200.

Prime Factorization of 200

The prime factorization of 200 is:

• 200 = 2 × 100
• 100 = 2 × 50
• 50 = 2 × 25
• 25 = 5 × 5

Therefore, the prime factors of 200 are: 2, 2, 2, 5, 5.

Simplifying the Radical

We can simplify the square root of 200 by grouping the prime factors into pairs:

\[
\sqrt{200} = \sqrt{2 \times 2 \times 2 \times 5 \times 5}
\]

We can take out the pairs of prime factors from under the square root:

\[
\sqrt{200} = \sqrt{(2 \times 2) \times (5 \times 5) \times 2} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2}
\]

Final Answer

Thus, the square root of 200 in its simplest radical form is:

\[
\boxed{10\sqrt{2}}
\]

Understanding how to simplify the square root of 200 in radical form is a fundamental skill in algebra. This process involves breaking down the number into its prime factors and simplifying the expression to its most concise form. In this guide, we will take you through each step to transform the square root of 200 into its simplest radical form.

The concept of square roots is essential in various fields of mathematics and science. Simplifying square roots helps in solving equations, understanding geometric properties, and more. Let’s delve into the process:

1. Prime Factorization: Begin by finding the prime factors of 200. This involves dividing the number into its smallest prime components.
2. Grouping Factors: Once we have the prime factors, we group them in pairs. Pairs of prime factors can be taken out from under the square root sign.
3. Simplifying the Expression: Finally, we simplify the expression by multiplying the numbers outside the radical and leaving any unpaired factors under the square root.

By following these steps, we can convert the square root of 200 into its simplest radical form, making it easier to work with in mathematical problems.

Square roots are a fundamental concept in mathematics, representing a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3 because \(3 \times 3 = 9\). This operation is crucial in various areas of math and science.

The square root is symbolized by the radical sign (√). When we talk about the square root of a number \(x\), we are looking for a number \(y\) such that \(y^2 = x\). In equation form, this is written as:

\[
\sqrt{x} = y \quad \text{if and only if} \quad y^2 = x
\]

There are a few key points to understand about square roots:

• Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For example, both 4 and -4 are square roots of 16.
• Principal Square Root: When we refer to "the square root" of a number, we usually mean the principal (non-negative) square root.
• Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are integers.
• Non-Perfect Squares: Numbers that do not have integer square roots are called non-perfect squares. Their square roots are irrational numbers that can be expressed in radical form.

Understanding how to work with square roots, especially non-perfect squares, is essential for simplifying expressions and solving equations. In the case of the square root of 200, we will simplify it into its radical form through prime factorization and grouping.

The radical form of a number involves expressing it as a product of its simplest factors under the square root symbol (√). This form is often used to simplify complex expressions and to make them easier to work with in mathematical operations.

For a given number \(x\), its radical form is represented as:

\[
\sqrt{x}
\]

Here are the steps to understand the radical form in more detail:

1. Identifying the Radicand: The number inside the square root symbol is called the radicand. For example, in \(\sqrt{200}\), 200 is the radicand.
2. Simplifying the Radicand: The goal is to express the radicand as a product of its prime factors. For instance, the prime factorization of 200 is \(2^3 \times 5^2\).
3. Grouping the Factors: Next, group the prime factors into pairs. Each pair of identical factors can be taken out from under the square root. For \(200 = 2^3 \times 5^2\), we can group the factors as \((2 \times 2) \times (5 \times 5) \times 2\).
4. Extracting the Pairs: Each pair of factors comes out of the square root as a single factor. So, \(\sqrt{(2 \times 2) \times (5 \times 5) \times 2} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2}\).

Thus, the radical form allows us to break down and simplify expressions involving square roots, making complex calculations more manageable. The square root of 200 in its simplest radical form is \(10\sqrt{2}\), showing the importance and utility of understanding and using the radical form.

Simplifying the square root of 200 involves breaking it down into its simplest radical form. Follow these detailed steps to achieve this:

1. Find the Prime Factorization of 200:
   • Start by dividing 200 by the smallest prime number, which is 2.
   • 200 ÷ 2 = 100
   • 100 ÷ 2 = 50
   • 50 ÷ 2 = 25
   • 25 ÷ 5 = 5
   • 5 ÷ 5 = 1

   So, the prime factorization of 200 is \(2^3 \times 5^2\).

2. Express the Square Root with Prime Factors:

   Write the square root of 200 using its prime factors:

   \[
   \sqrt{200} = \sqrt{2^3 \times 5^2}
   \]

3. Group the Prime Factors in Pairs:

   Identify and group the pairs of prime factors under the square root:

   \[
   \sqrt{2^3 \times 5^2} = \sqrt{(2 \times 2) \times (5 \times 5) \times 2}
   \]

4. Simplify the Expression:

   Take out each pair of prime factors from under the square root, and multiply them:

   \[
   \sqrt{(2 \times 2) \times (5 \times 5) \times 2} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2}
   \]

Therefore, the simplified radical form of the square root of 200 is \(10\sqrt{2}\). This method ensures that we express the square root in the simplest and most manageable form, useful for further mathematical calculations and problem-solving.

Simplifying a radical involves grouping the factors of the radicand (the number inside the square root) into pairs and simplifying the expression. Here’s a step-by-step guide to grouping and simplifying the square root of 200:

1. Prime Factorization:

   First, express 200 as a product of its prime factors:

   \[
   200 = 2^3 \times 5^2
   \]

2. Write the Radical with Prime Factors:

   Express the square root of 200 using its prime factors:

   \[
   \sqrt{200} = \sqrt{2^3 \times 5^2}
   \]

3. Group the Prime Factors:

   Group the prime factors into pairs. Each pair of the same factors can be taken out from under the square root as a single factor:

   \[
   \sqrt{2^3 \times 5^2} = \sqrt{(2 \times 2) \times 2 \times (5 \times 5)}
   \]

4. Simplify the Expression:

   Take each pair out of the square root and multiply them:

   \[
   \sqrt{(2 \times 2) \times 2 \times (5 \times 5)} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2}
   \]

By grouping and simplifying, we have expressed the square root of 200 in its simplest radical form as \(10\sqrt{2}\). This process makes the expression more manageable and easier to work with in further mathematical operations.

To express the square root of 200 in its simplest radical form, we need to follow a systematic approach involving prime factorization, grouping, and simplifying. Here are the detailed steps:

1. Find the Prime Factorization of 200:

   Break down 200 into its prime factors:

   • 200 ÷ 2 = 100
   • 100 ÷ 2 = 50
   • 50 ÷ 2 = 25
   • 25 ÷ 5 = 5
   • 5 ÷ 5 = 1

   Therefore, the prime factorization of 200 is:

   \[
   200 = 2^3 \times 5^2
   \]

2. Express the Square Root Using Prime Factors:

   Write the square root of 200 with its prime factors:

   \[
   \sqrt{200} = \sqrt{2^3 \times 5^2}
   \]

3. Group the Prime Factors:

   Group the factors in pairs:

   \[
   \sqrt{2^3 \times 5^2} = \sqrt{(2 \times 2) \times 2 \times (5 \times 5)}
   \]

4. Extract the Pairs from the Radical:

   Each pair of identical factors can be taken out of the square root as a single factor:

   \[
   \sqrt{(2 \times 2) \times 2 \times (5 \times 5)} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2}
   \]

Therefore, the square root of 200 in its simplest radical form is \(10\sqrt{2}\). This simplified expression makes it easier to work with and understand in various mathematical contexts.

The square root of 200, expressed as \( \sqrt{200} = 10\sqrt{2} \), has various practical applications in different fields. Here are some key areas where this mathematical concept is utilized:

• Geometry and Construction: In geometry, the square root of 200 can be used to determine distances and measurements. For example, if a right triangle has legs of lengths 10 units and 10 units, the hypotenuse will be \( \sqrt{10^2 + 10^2} = \sqrt{200} = 10\sqrt{2} \) units. This is crucial in construction for accurate measurements and ensuring structures are built correctly.
• Physics: The square root of 200 appears in formulas and calculations in physics. For instance, when dealing with vectors and magnitudes, understanding and simplifying square roots helps in determining resultant forces and displacements.
• Engineering: Engineers often encounter square roots when dealing with stress, strain, and other calculations related to materials and structural integrity. Simplifying \( \sqrt{200} \) to \( 10\sqrt{2} \) can make complex formulas more manageable and easier to work with.
• Computer Graphics: In computer graphics, distances and transformations often require square root calculations. For instance, calculating the Euclidean distance between points in a 2D or 3D space may involve \( \sqrt{200} \).
• Art and Design: Artists and designers use the square root of 200 to achieve precise proportions and symmetry in their work. This mathematical concept helps in creating aesthetically pleasing designs that adhere to specific measurements.
• Finance: Financial models and algorithms sometimes use square roots in risk assessment and optimization problems. Understanding \( \sqrt{200} \) can be crucial in scenarios where square root calculations are necessary.
• Education: Teaching and learning about square roots, including \( \sqrt{200} \), helps students grasp fundamental mathematical concepts that are applied in various real-world situations.

By understanding and utilizing \( \sqrt{200} \) in these applications, individuals can solve practical problems more effectively and enhance their analytical skills.

The square root of 200, represented as $\sqrt{200}$, can be visualized in several ways to aid understanding and provide a clear picture of this mathematical concept. Below are some key visual representations:

1. Geometric Representation

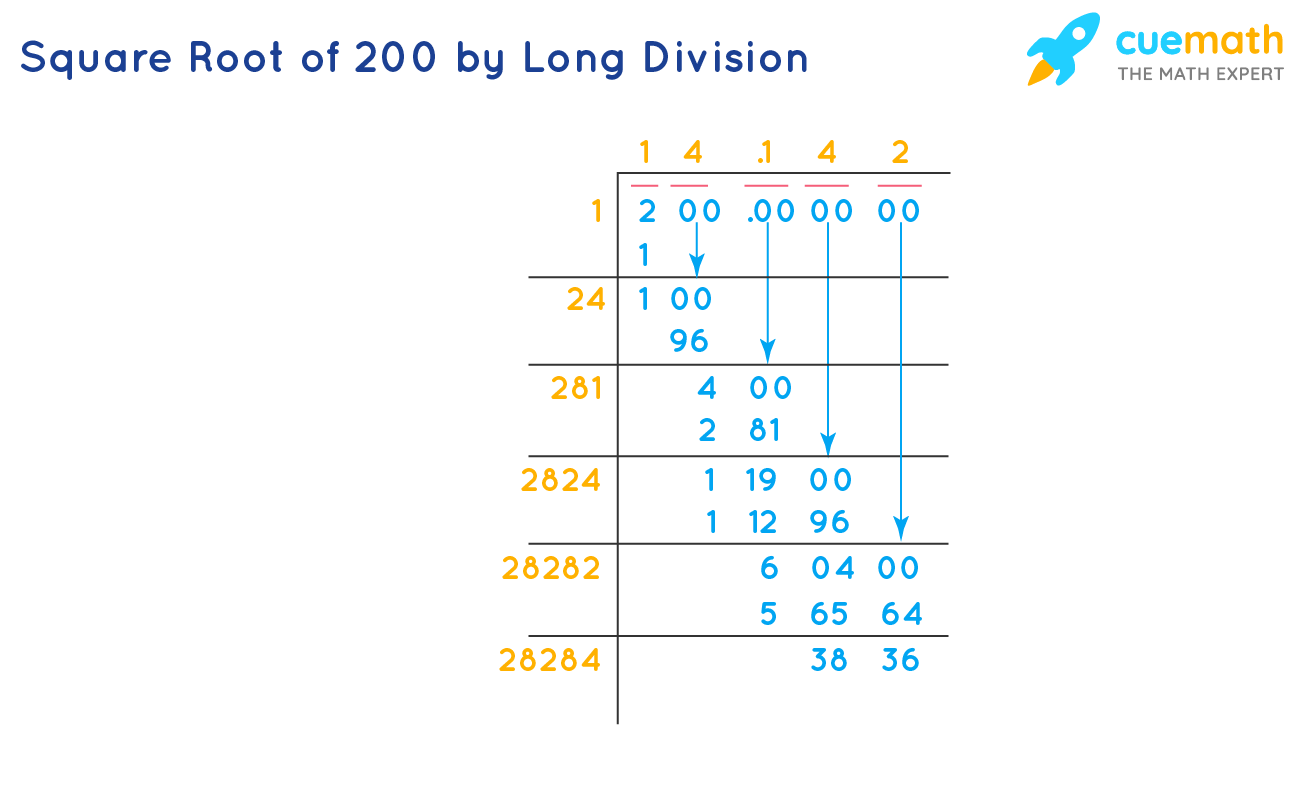
To visualize $\sqrt{200}$ geometrically, consider a square with an area of 200 square units. The length of each side of this square is $\sqrt{200}$ units, which is approximately 14.14 units.

2. Number Line Representation

On a number line, $\sqrt{200}$ lies between 14 and 15. More precisely, it is approximately 14.14. This placement helps in understanding its magnitude relative to whole numbers.

3. Simplified Radical Form

The simplified radical form of $\sqrt{200}$ is $10\sqrt{2}$. This form is derived through prime factorization:

$$


200

=


2
×
100


=
10

2

4. Graphical Representation

A graphical plot can also represent $\sqrt{200}$. Consider a parabola y = x² and a horizontal line y = 200. The x-coordinate where these two graphs intersect gives the value of $\sqrt{200}$.

5. Approximate Decimal Form

The approximate decimal form of $\sqrt{200}$ is 14.142. This is often used for practical calculations and can be visualized on a digital calculator display.

These visualizations provide different perspectives on understanding $\sqrt{200}$ and its applications in various mathematical contexts.

When working with square roots and simplifying radicals, there are several common mistakes that can lead to incorrect results. Here are some of the most frequent errors to be aware of and tips to avoid them:

• Ignoring Prime Factorization: One common mistake is skipping the step of prime factorization. Always break down the number into its prime factors to ensure a thorough simplification. For example, for √200, you should first factor it into prime numbers: 200 = 2^3 * 5^2.
• Misidentifying Perfect Squares: Incorrectly identifying pairs of factors that form perfect squares can result in incorrect simplification. Ensure that you correctly group the factors. For √200, group the factors as (2^2 * 5^2) and (2), then simplify to 10√2.
• Overlooking the Radical Sign: Sometimes, students forget to include the radical sign after simplifying the expression, changing the meaning of the result. For instance, leaving out the radical in √200 can lead to incorrect answers like 10 instead of 10√2.
• Incorrectly Combining Radicals: Only radicals with the same radicand (the number inside the radical) can be combined. Avoid combining radicals with different radicands, as it leads to incorrect results. For example, √200 cannot be combined directly with √50 without simplification.
• Failing to Rationalize the Denominator: When radicals appear in the denominator, it is crucial to rationalize them. This involves multiplying both the numerator and denominator by a suitable radical to eliminate the radical in the denominator. For example, if you have 1/√2, multiply by √2/√2 to get √2/2.

By being mindful of these pitfalls, you can improve your accuracy in simplifying radicals and develop a deeper understanding of the underlying mathematical principles.

Below are some practice problems to help you understand how to simplify and work with the square root of 200 in its radical form. Follow the step-by-step solutions to enhance your understanding.

1. Problem: Simplify √200

   Solution:

   1. Prime factorize 200: 200 = 2 × 2 × 2 × 5 × 5
   2. Group the prime factors into pairs: (2 × 2) × (5 × 5) × 2
   3. Take the square root of each pair and multiply them together: √(2^2) × √(5^2) × √2 = 2 × 5 × √2 = 10√2
   4. Therefore, √200 = 10√2

2. Problem: Simplify the expression 3√200 + 2√50

   Solution:

   1. Simplify each radical separately:
   • √200 = 10√2
   • √50 = √(2 × 5 × 5) = 5√2
   2. Substitute back into the expression: 3(10√2) + 2(5√2) = 30√2 + 10√2
   3. Combine like terms: 40√2
   4. Therefore, 3√200 + 2√50 = 40√2

3. Problem: Solve the equation √200 = x

   Solution:

   1. Recognize that the radical form of √200 is 10√2
   2. Therefore, x = 10√2

4. Problem: Rationalize the denominator of the expression 1/√200

   Solution:

   1. Multiply the numerator and denominator by √200 to get rid of the radical in the denominator: (1/√200) × (√200/√200)
   2. This gives (√200)/200
   3. Since √200 = 10√2, substitute to get: (10√2)/200
   4. Simplify the fraction: 10√2/200 = √2/20
   5. Therefore, 1/√200 = √2/20

These practice problems demonstrate the process of simplifying, adding, solving, and rationalizing expressions involving the square root of 200. Keep practicing to become more comfortable with these concepts.

Understanding advanced concepts related to radicals can significantly deepen your mathematical knowledge and problem-solving skills. Here are some key concepts and techniques:

1. Rationalizing the Denominator

When a radical appears in the denominator of a fraction, it's often necessary to "rationalize" it, which means to eliminate the radical. This is done by multiplying the numerator and the denominator by a conjugate or an appropriate radical expression.

• For example, to rationalize \(\frac{2}{\sqrt{5}}\), multiply by \(\frac{\sqrt{5}}{\sqrt{5}}\): \[ \frac{2}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{2\sqrt{5}}{5} \]
• For more complex expressions, such as \(\frac{1}{\sqrt{3} + \sqrt{2}}\), multiply by the conjugate \(\sqrt{3} - \sqrt{2}\): \[ \frac{1}{\sqrt{3} + \sqrt{2}} \times \frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} - \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3})^2 - (\sqrt{2})^2} = \frac{\sqrt{3} - \sqrt{2}}{3 - 2} = \sqrt{3} - \sqrt{2} \]

2. Conjugate Radicals

Conjugate radicals are used to rationalize denominators and to simplify expressions involving radicals. The conjugate of \((a + b\sqrt{c})\) is \((a - b\sqrt{c})\).

• Multiplying conjugates results in a rational number: \[ (a + b\sqrt{c})(a - b\sqrt{c}) = a^2 - (b\sqrt{c})^2 = a^2 - b^2c \]

3. Operations with Radicals

Performing arithmetic operations with radicals follows specific rules:

• Addition and Subtraction: Combine like radicals (radicals with the same radicand): \[ 2\sqrt{3} + 5\sqrt{3} = 7\sqrt{3} \]
• Multiplication: Multiply the coefficients and the radicands separately: \[ (2\sqrt{3})(4\sqrt{5}) = (2 \times 4)(\sqrt{3} \times \sqrt{5}) = 8\sqrt{15} \]
• Division: Simplify by dividing the coefficients and the radicands: \[ \frac{6\sqrt{8}}{3\sqrt{2}} = 2\sqrt{4} = 4 \]

4. Solving Radical Equations

Equations involving radicals can be solved by isolating the radical and then squaring both sides of the equation. Be sure to check for extraneous solutions, as squaring can introduce invalid solutions.

• Example: Solve \(\sqrt{x+3} = x - 1\)
  1. Isolate the radical: \(\sqrt{x+3} = x - 1\)
  2. Square both sides: \(x + 3 = (x - 1)^2\)
  3. Expand and simplify: \(x + 3 = x^2 - 2x + 1\)
  4. Rearrange to form a quadratic equation: \(x^2 - 3x - 2 = 0\)
  5. Solve the quadratic equation: \(x = 1\) or \(x = -2\)
  6. Check the solutions: Only \(x = 1\) is valid in the original equation.

5. Higher-Order Radicals

Radicals of higher order, such as cube roots, follow similar rules but require different approaches for simplification and rationalization. For example, the cube root of a number involves finding a value that, when multiplied by itself three times, equals the original number.

• Example: \(\sqrt[3]{8} = 2\), because \(2^3 = 8\).

Here are some frequently asked questions about the square root of 200 in its radical form, along with detailed answers to help you understand the concept better:

• What is the simplified version of the square root of 200?

  The square root of 200 in its simplest radical form is \(10\sqrt{2}\).

• Is 200 a perfect square?

  No, 200 is not a perfect square. A perfect square is a number that has an integer as its square root, such as 100 (which is \(10^2\)).

• Is the square root of 200 rational or irrational?

  The square root of 200 is irrational. An irrational number cannot be expressed as a simple fraction; its decimal form is non-terminating and non-repeating.

• Can the square root of 200 be simplified?

  Yes, the square root of 200 can be simplified to \(10\sqrt{2}\). This is done by finding the prime factorization of 200, which is \(2^3 \times 5^2\), and then simplifying the radicals.

• What is the approximate decimal value of the square root of 200?

  The approximate decimal value of \(\sqrt{200}\) is about 14.142. This can be useful for practical calculations where an exact radical form is not required.

• What are some practical applications of the square root of 200?

  The square root of 200 is used in various fields such as architecture for calculating dimensions, in engineering for design optimization, and in finance for risk assessment.

• How can I use the square root of 200 in geometry?

  In geometry, \(\sqrt{200}\) can be used to find the length of the diagonal of a square with an area of 200 square units. This is because the diagonal \(d\) of a square with side length \(s\) is given by \(d = s\sqrt{2}\), and here \(s = \sqrt{200}\).

Understanding the square root of 200 in its radical form as \(10\sqrt{2}\) provides both a foundational mathematical skill and practical insights into its applications. Simplifying radicals, such as \(\sqrt{200}\), involves breaking down the number into its prime factors and grouping them appropriately, allowing for the simplest radical form.

This comprehensive guide has covered various aspects of \(\sqrt{200}\), from the definition and simplification process to practical applications and visual representations. By mastering the steps to simplify \(\sqrt{200}\), you can approach other similar mathematical problems with confidence.

Remember, the key points include:

• Prime factorization of 200 results in \(2^3 \times 5^2\).
• Grouping these factors leads to \(10\sqrt{2}\).
• \(\sqrt{200}\) in decimal form is approximately 14.142, demonstrating its irrational nature.

Additionally, visual aids, practice problems, and advanced concepts related to radicals enrich your understanding and help avoid common mistakes. With these tools, you are well-equipped to handle various mathematical challenges involving square roots and radicals.

We hope this guide has been informative and helpful. Continue practicing and exploring further to enhance your mathematical skills and knowledge.