Topic 5 square rooted: The square root of 5, often represented as \( \sqrt{5} \), is a captivating mathematical concept with intriguing properties and applications. In this article, we'll explore its significance, methods of calculation, and its role in various fields. Discover why the square root of 5 continues to fascinate mathematicians and enthusiasts alike.
Table of Content
- Understanding the Square Root of 5
- Introduction to Square Roots
- What is the Square Root of 5?
- Mathematical Definition of Square Root
- Properties of the Square Root of 5
- Decimal Representation of the Square Root of 5
- Methods to Calculate the Square Root of 5
- Using Long Division Method
- Applying Newton's Method
- Utilizing Calculators for Square Root Calculation
- Geometric Interpretation of the Square Root of 5
- Real-life Applications of the Square Root of 5
- Square Root of 5 in Algebra
- Square Root of 5 in Geometry
- Square Root of 5 in Number Theory
- Importance of Irrational Numbers
- Understanding Non-repeating Decimals
- Historical Context of Square Roots
- YOUTUBE:
Understanding the Square Root of 5
The square root of 5, denoted as \( \sqrt{5} \), is an important mathematical concept with applications in various fields such as algebra, geometry, and number theory. It is an irrational number, which means it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating.
Decimal Representation
The approximate value of \( \sqrt{5} \) is:
\[
\sqrt{5} \approx 2.23606797749979
\]
Properties of \( \sqrt{5} \)
- \( \sqrt{5} \) is an irrational number.
- It cannot be expressed as a ratio of two integers.
- Its decimal expansion is non-repeating and non-terminating.
Geometric Interpretation
Geometrically, \( \sqrt{5} \) can be represented as the length of the diagonal of a rectangle with side lengths 1 and 2:
If you have a rectangle with sides of 1 and 2 units, the length of the diagonal \( d \) is given by the Pythagorean theorem:
\[
d = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}
\]
Uses in Mathematics
The square root of 5 appears in various mathematical contexts, including:
- Algebra: In solving quadratic equations where the discriminant involves 5.
- Geometry: In calculations involving right triangles, circles, and other shapes.
- Number Theory: In the study of Diophantine equations and continued fractions.
Calculating \( \sqrt{5} \)
There are several methods to calculate \( \sqrt{5} \) with high precision, including:
- Long Division Method: A manual method for finding square roots.
- Newton's Method: An iterative numerical method for approximating roots.
- Using a Calculator: Most scientific calculators can directly compute \( \sqrt{5} \).
Conclusion
The square root of 5 is a fascinating number with rich mathematical properties and numerous applications. Understanding its characteristics and methods to compute it can enhance one's mathematical knowledge and problem-solving skills.

READ MORE:
Introduction to Square Roots
Square roots are fundamental concepts in mathematics, representing a number that, when multiplied by itself, yields the original number. Understanding square roots is essential for various mathematical operations and real-world applications. Here, we delve into the concept of square roots, using the square root of 5 as a primary example.
Mathematically, the square root of a number \( x \) is denoted as \( \sqrt{x} \), and it satisfies the equation:
\[
\sqrt{x} \times \sqrt{x} = x
\]
For example, \( \sqrt{5} \) is the number that, when squared, equals 5:
\[
\sqrt{5} \times \sqrt{5} = 5
\]
Properties of Square Roots
- Square roots of positive numbers are always non-negative.
- The square root of a perfect square (e.g., 4, 9, 16) is an integer.
- The square root of non-perfect squares (e.g., 2, 3, 5) is an irrational number, meaning it cannot be expressed as a simple fraction.
Calculation Methods
There are several methods to calculate square roots, ranging from simple estimations to complex algorithms. Some of the common methods include:
- Prime Factorization: Breaking down the number into its prime factors can simplify the calculation of square roots for perfect squares.
- Long Division Method: A manual method that involves iterative division and averaging to approximate the square root.
- Newton's Method: Also known as the Newton-Raphson method, this is an iterative numerical method for finding successively better approximations to the roots (or zeroes) of a real-valued function.
Importance of Square Roots
Square roots have significant importance in various fields, including:
- Geometry: Used to determine distances, areas, and volumes in geometric shapes.
- Physics: Applied in formulas for motion, energy, and wave functions.
- Engineering: Essential in design calculations, structural analysis, and signal processing.
- Computer Science: Utilized in algorithms, graphics rendering, and data analysis.
Understanding the concept of square roots provides a strong foundation for further mathematical learning and practical problem-solving skills. As we continue, we will explore the specific case of the square root of 5, its properties, and its applications.
What is the Square Root of 5?
The square root of 5, denoted as \( \sqrt{5} \), is a number that, when multiplied by itself, equals 5. Mathematically, it can be expressed as:
\[
\sqrt{5} \times \sqrt{5} = 5
\]
\( \sqrt{5} \) is an irrational number, meaning it cannot be expressed as a simple fraction. Its decimal representation is non-terminating and non-repeating. The approximate value of \( \sqrt{5} \) is:
\[
\sqrt{5} \approx 2.23606797749979
\]
Properties of the Square Root of 5
- \( \sqrt{5} \) is an irrational number.
- Its decimal expansion is infinite and non-repeating.
- It is greater than 2 and less than 3.
Methods to Calculate \( \sqrt{5} \)
Several methods can be used to calculate \( \sqrt{5} \) with high precision:
- Long Division Method: A manual method for finding square roots that involves dividing and averaging.
- Newton's Method: An iterative numerical method for approximating roots, also known as the Newton-Raphson method. It uses the formula:
\[
where \( x_n \) is the current approximation.
x_{n+1} = \frac{1}{2} \left( x_n + \frac{5}{x_n} \right)
\] - Using a Calculator: Most scientific calculators have a square root function that can directly compute \( \sqrt{5} \).
Geometric Interpretation
Geometrically, the square root of 5 can be visualized as the length of the diagonal of a rectangle with side lengths 1 and 2 units. Using the Pythagorean theorem:
\[
d = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}
\]
Applications of the Square Root of 5
The square root of 5 appears in various mathematical contexts, including:
- Algebra: Solving quadratic equations where the discriminant involves 5.
- Geometry: Calculations involving right triangles, circles, and other geometric shapes.
- Number Theory: In the study of Diophantine equations and continued fractions.
- Physics and Engineering: Applied in formulas and design calculations.
Understanding \( \sqrt{5} \) is essential for a wide range of mathematical and scientific endeavors, making it a valuable concept to grasp thoroughly.
Mathematical Definition of Square Root
The square root of a number is a value that, when multiplied by itself, yields the original number. It is denoted by the radical symbol \( \sqrt{} \). Formally, if \( y \) is the square root of \( x \), then:
\[
y = \sqrt{x} \quad \text{and} \quad y^2 = x
\]
For example, the square root of 25 is 5, because:
\[
5^2 = 25 \quad \text{and} \quad \sqrt{25} = 5
\]
Square roots can be classified into two categories:
- Perfect Squares: Numbers that have integer square roots (e.g., 1, 4, 9, 16).
- Non-Perfect Squares: Numbers that do not have integer square roots, resulting in irrational numbers (e.g., 2, 3, 5).
The square root function is defined only for non-negative numbers in the set of real numbers. For a given non-negative real number \( x \), there exists a non-negative number \( y \) such that:
\[
y = \sqrt{x} \quad \text{and} \quad y^2 = x
\]
Principal Square Root
The principal square root of a non-negative number \( x \) is the non-negative root of \( x \). It is denoted as \( \sqrt{x} \). For instance:
\[
\sqrt{16} = 4 \quad \text{because} \quad 4^2 = 16
\]
Negative Square Roots
Every positive number has two square roots: one positive (principal square root) and one negative. However, when using the radical symbol \( \sqrt{} \), it typically refers to the principal (positive) square root:
\[
\sqrt{9} = 3 \quad \text{but also} \quad -\sqrt{9} = -3
\]
Properties of Square Roots
- Non-negativity: For any non-negative real number \( x \), \( \sqrt{x} \geq 0 \).
- Product Property: For any non-negative real numbers \( a \) and \( b \):
\[
\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}
\] - Quotient Property: For any non-negative real numbers \( a \) and \( b \) (with \( b \neq 0 \)):
\[
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]
Understanding the mathematical definition and properties of square roots is crucial for solving a wide range of mathematical problems, from basic arithmetic to advanced calculus and beyond.
Properties of the Square Root of 5
The square root of 5, denoted as \( \sqrt{5} \), is a unique and interesting number with several distinct properties. Here, we explore the key characteristics and mathematical properties of \( \sqrt{5} \).
Irrational Number
\( \sqrt{5} \) is an irrational number, meaning it cannot be expressed as a simple fraction. Its decimal representation is non-terminating and non-repeating:
\[
\sqrt{5} \approx 2.23606797749979\ldots
\]
This non-repeating, non-terminating nature is a hallmark of irrational numbers.
Algebraic Properties
- \(<\textbf>Identity: The square of \( \sqrt{5} \) is 5:
\[
(\sqrt{5})^2 = 5
\] - Product Property: For any non-negative real numbers \( a \) and \( b \):
\[
Applying this to 5, we get:
\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}
\]\[
\sqrt{5 \times 4} = \sqrt{5} \times \sqrt{4} = \sqrt{20}
\] - Quotient Property: For any non-negative real numbers \( a \) and \( b \) (with \( b \neq 0 \)):
\[
Applying this to 5, we get:
\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}
\]\[
\sqrt{\frac{5}{4}} = \frac{\sqrt{5}}{\sqrt{4}} = \frac{\sqrt{5}}{2}
\]
Geometric Interpretation
Geometrically, \( \sqrt{5} \) can be visualized as the length of the diagonal of a rectangle with side lengths 1 and 2 units. Using the Pythagorean theorem, we find:
\[
\text{Diagonal} = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}
\]
This geometric interpretation helps in understanding the spatial representation of \( \sqrt{5} \).
Applications in Mathematics and Science
- Quadratic Equations: The square root of 5 often appears in solutions to quadratic equations where the discriminant is 5.
- Geometry: Calculations involving right triangles, circles, and other shapes frequently use \( \sqrt{5} \).
- Number Theory: \( \sqrt{5} \) is significant in the study of continued fractions and Diophantine equations.
- Physics and Engineering: Various formulas and design calculations involve \( \sqrt{5} \).
Approximation Methods
While \( \sqrt{5} \) is irrational, it can be approximated using various methods such as:
- Long Division Method: A manual iterative method for finding square roots.
- Newton's Method: An iterative numerical technique for approximating square roots:
\[
x_{n+1} = \frac{1}{2} \left( x_n + \frac{5}{x_n} \right)
\] - Using a Calculator: Most scientific calculators can compute \( \sqrt{5} \) directly.
Understanding the properties of \( \sqrt{5} \) enhances our comprehension of mathematical concepts and their real-world applications.

Decimal Representation of the Square Root of 5
The square root of 5, denoted as \( \sqrt{5} \), is an irrational number. This means that its decimal representation is non-terminating and non-repeating. Understanding the decimal representation of \( \sqrt{5} \) provides insight into its complexity and how it can be approximated.
Approximate Decimal Value
The approximate value of \( \sqrt{5} \) to several decimal places is:
\[
\sqrt{5} \approx 2.23606797749979
\]
Characteristics of the Decimal Representation
- Non-Terminating: The decimal expansion of \( \sqrt{5} \) continues infinitely without ending.
- Non-Repeating: The digits in the decimal expansion do not form a repeating pattern.
Methods for Approximating \( \sqrt{5} \)
Several methods can be used to approximate the decimal value of \( \sqrt{5} \) with high precision:
- Long Division Method: A manual method that involves iterative division to achieve a precise approximation. This method is labor-intensive but provides accurate results.
- Newton's Method (Newton-Raphson Method): An iterative numerical technique used to approximate roots of real-valued functions. For \( \sqrt{5} \), the iterative formula is:
\[
Starting with an initial guess \( x_0 \), this method rapidly converges to the actual value.
x_{n+1} = \frac{1}{2} \left( x_n + \frac{5}{x_n} \right)
\] - Using a Calculator: Modern scientific calculators and computer software can compute \( \sqrt{5} \) to a high degree of accuracy with ease.
Practical Applications
The decimal representation of \( \sqrt{5} \) is used in various practical applications, including:
- Engineering and Design: Precise measurements and calculations in fields such as civil, mechanical, and electrical engineering.
- Computer Graphics: Calculations for rendering and modeling that require high precision.
- Science and Research: Accurate data analysis and experimentation in physics, chemistry, and other scientific disciplines.
Understanding the decimal representation of \( \sqrt{5} \) and the methods to approximate it are crucial for various scientific and engineering tasks, providing the precision necessary for accurate results.
Methods to Calculate the Square Root of 5
Calculating the square root of 5, denoted as \( \sqrt{5} \), can be achieved through various methods, ranging from manual calculations to using advanced algorithms. Here, we outline several methods to calculate \( \sqrt{5} \) with detailed steps.
1. Long Division Method
The long division method is a manual technique that provides a step-by-step approach to finding square roots. Here’s how it works:
- Step 1: Group the digits of the number in pairs, starting from the decimal point. For 5, consider it as 5.000000.
- Step 2: Find the largest number whose square is less than or equal to the first group. In this case, 2 because \( 2^2 = 4 \leq 5 \).
- Step 3: Subtract the square of this number from the first group and bring down the next pair of digits.
- Step 4: Double the quotient obtained so far (which is 2) and use it as a new divisor. Find a digit that, when added to this new divisor and multiplied by itself, gives a product less than or equal to the current number.
- Step 5: Repeat the process with the remainder and the next pairs of digits until the desired precision is achieved.
2. Newton's Method (Newton-Raphson Method)
Newton's Method is an iterative numerical technique that rapidly converges to the accurate value of a square root. The formula used is:
\[
x_{n+1} = \frac{1}{2} \left( x_n + \frac{5}{x_n} \right)
\]
Here’s how to apply it:
- Step 1: Choose an initial guess \( x_0 \). A good starting point for \( \sqrt{5} \) is 2.2.
- Step 2: Apply the formula to get a new approximation \( x_1 \).
- Step 3: Repeat the process with \( x_1 \) to get \( x_2 \), and so on, until the difference between successive approximations is within a desired tolerance.
3. Using a Calculator
Most scientific calculators and computer software can compute square roots directly. To find \( \sqrt{5} \) using a calculator:
- Step 1: Enter the number 5.
- Step 2: Press the square root (√) function key.
- Step 3: The calculator will display the approximate value of \( \sqrt{5} \).
4. Continued Fractions
Continued fractions provide a way to express square roots as a sequence of integer quotients. For \( \sqrt{5} \), the continued fraction representation is:
\[
\sqrt{5} = 2 + \frac{1}{4 + \frac{1}{4 + \frac{1}{4 + \cdots}}}
\]
This method is more complex but provides a deeper understanding of the structure of irrational numbers.
Each of these methods has its own advantages, from the intuitive steps of long division to the rapid convergence of Newton's method and the simplicity of using a calculator. Understanding and applying these methods can greatly enhance one's mathematical skills and accuracy in calculations.
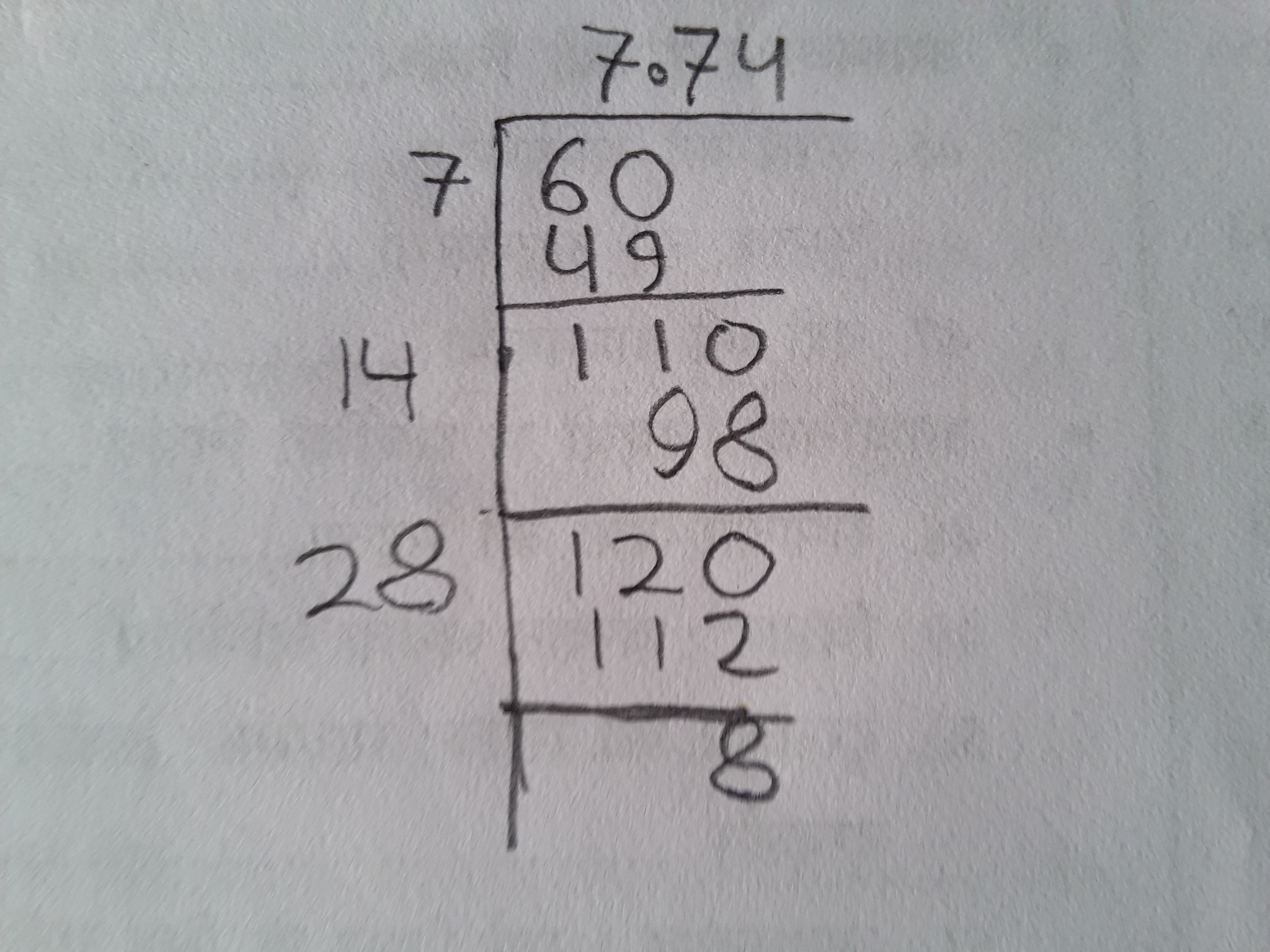
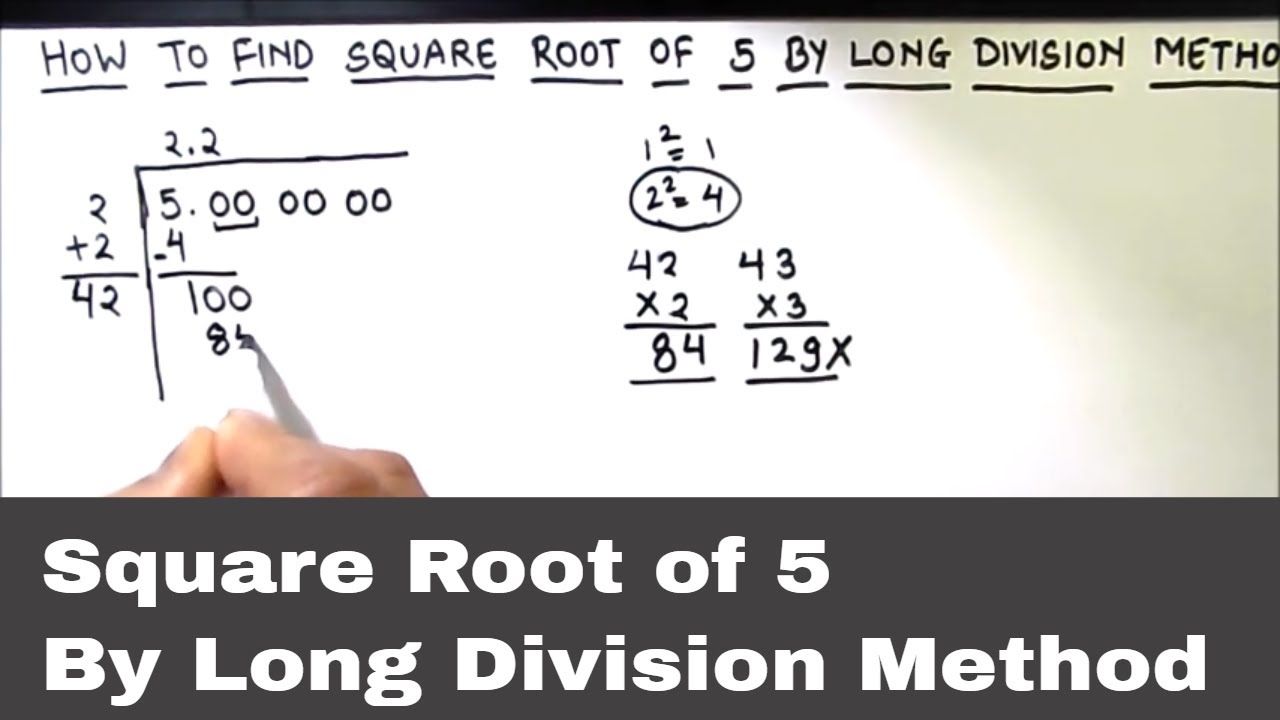
Using Long Division Method
The long division method is a straightforward approach to approximate the square root of a number, such as √5. Here's how you can apply it:
- Start by grouping the digits of the number into pairs from the decimal point (if applicable). For √5, we focus on the number 5.
- Identify the largest integer whose square is less than or equal to the first group. For 5, the integer closest to √5 is 2 (since 2² = 4).
- Subtract the square of this integer from the first group, then bring down the next pair of digits (00 in this case).
- Double the quotient (2), and write down the largest digit (0) such that when 20 is multiplied by the digit, it's equal to or less than the current dividend (100 in this case).
- Repeat steps 3 and 4 until the desired level of accuracy is achieved.
This method allows for a manual computation of square roots without the need for advanced calculators, making it useful in educational contexts and situations where precise approximations are sufficient.
Applying Newton's Method
Newton's method is an iterative approach to find the square root of a number, such as √5. Here's a detailed step-by-step process:
- Start with an initial guess \( x_0 \). For √5, a reasonable initial guess could be 2.
- Iteratively refine the guess using the formula:
- Calculate \( x_1 \) using the initial guess \( x_0 \).
- Repeat the calculation, substituting \( x_1 \) back into the formula to get \( x_2 \).
- Continue iterating until the difference between successive values of \( x_n \) is within an acceptable tolerance level.
| \( x_{n+1} = \frac{1}{2} \left( x_n + \frac{5}{x_n} \right) \) |
Newton's method converges rapidly to the square root of a number and is widely used in numerical analysis due to its efficiency. It provides a more precise result compared to simpler methods like long division, especially for higher accuracy requirements.
Utilizing Calculators for Square Root Calculation
Modern calculators, both handheld and software-based, offer efficient ways to compute square roots, including √5. Here’s how you can use them:
- Turn on your calculator and ensure it's set to handle square root operations.
- Enter the number for which you want to find the square root, in this case, 5.
- Press the square root (√) button on the calculator.
- Depending on the calculator, the result may appear instantly or you may need to press an additional button to see the result.
- Verify the result against expected values or use it in further calculations as needed.
Calculators provide accurate results and are ideal for quick calculations in everyday situations or when precision is critical, such as in scientific or financial contexts.
Geometric Interpretation of the Square Root of 5
The square root of 5 (√5) can be geometrically interpreted in several ways:
- Length of Diagonal: In a square with sides of length 1 unit, the diagonal has a length of √2. By scaling this square by a factor of √5, the diagonal of the scaled square would be √5 units.
- Golden Rectangle: The square root of 5 is related to the dimensions of a golden rectangle, where the ratio of the longer side to the shorter side is φ (phi), the golden ratio (approximately 1.618). The sides of a golden rectangle are in the ratio of φ:1, and its dimensions are such that when its smaller side is 1 unit, the longer side is φ units, and the diagonal length is √5 units.
- Geometric Construction: √5 can also be constructed geometrically using a compass and straightedge. This construction involves drawing specific geometric shapes that relate to the square root of 5, demonstrating its geometric properties.
These interpretations highlight the geometric significance and applications of √5 in various contexts, from architecture to mathematics and art.
Real-life Applications of the Square Root of 5
The square root of 5 (√5) has practical applications in various real-life scenarios:
- Engineering and Construction: √5 is used in calculating distances, especially diagonals, in structures such as bridges and buildings where precise measurements are crucial.
- Financial Calculations: In finance, √5 can be involved in calculating interest rates, volatility measures, and other financial metrics where square roots are used to model variability.
- Physics and Mechanics: √5 appears in equations related to waves, vibrations, and oscillations, where understanding amplitude and frequency involves square root calculations.
- Art and Design: Artists and designers use √5 proportions in creating aesthetically pleasing compositions, following principles such as the golden ratio and its derivatives.
- Technology: Algorithms in computing often utilize square root calculations, including in areas like image processing, cryptography, and data analysis.
These applications demonstrate the broad utility of √5 across disciplines, showing its importance beyond theoretical mathematics into practical everyday use.
Square Root of 5 in Algebra
The square root of 5, denoted as \( \sqrt{5} \), is an important irrational number in algebra that frequently appears in various mathematical contexts. In this section, we will explore how the square root of 5 is utilized in algebraic equations, expressions, and identities.
Solving Quadratic Equations
One common appearance of \( \sqrt{5} \) is in the solutions to quadratic equations. Consider the quadratic equation:
\[ x^2 - 5 = 0 \]
To solve for \( x \), we add 5 to both sides and then take the square root of both sides:
\[ x^2 = 5 \]
\[ x = \pm \sqrt{5} \]
Thus, the solutions are \( x = \sqrt{5} \) and \( x = -\sqrt{5} \).
Simplifying Algebraic Expressions
The square root of 5 can also be used to simplify algebraic expressions. For instance:
\[ \frac{2\sqrt{5}}{\sqrt{5}} = 2 \]
This simplification arises because \( \sqrt{5} \times \sqrt{5} = 5 \).
Using the Quadratic Formula
The quadratic formula, which provides solutions to the general quadratic equation \( ax^2 + bx + c = 0 \), often involves square roots. For example:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
In cases where the discriminant (\( b^2 - 4ac \)) equals 5, the square root of 5 will appear in the solutions:
\[ x = \frac{-b \pm \sqrt{5}}{2a} \]
Rationalizing Denominators
In algebra, it is often necessary to rationalize the denominator of a fraction. For example, to rationalize the denominator of \( \frac{1}{\sqrt{5}} \), we multiply the numerator and the denominator by \( \sqrt{5} \):
\[ \frac{1}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{5} \]
Algebraic Identities Involving \( \sqrt{5} \)
The square root of 5 can also be involved in algebraic identities, such as:
- \[ (\sqrt{5})^2 = 5 \]
- \[ (\sqrt{a} \times \sqrt{b}) = \sqrt{ab} \]
- \[ (\sqrt{5} + 1)(\sqrt{5} - 1) = 5 - 1 = 4 \]
Polynomials and Roots
The square root of 5 can be a root of certain polynomials. For example, \( x^2 - 5 \) has roots \( \sqrt{5} \) and \( -\sqrt{5} \). These roots can be used to factor the polynomial:
\[ x^2 - 5 = (x - \sqrt{5})(x + \sqrt{5}) \]
Examples and Practice Problems
Here are some practice problems to reinforce the concepts discussed:
- Solve the equation: \( x^2 - 5x + 6 = 0 \).
- Simplify the expression: \( \frac{3\sqrt{5} + 2\sqrt{5}}{\sqrt{5}} \).
- Rationalize the denominator: \( \frac{7}{2\sqrt{5}} \).
- Factor the polynomial: \( x^2 - 2x - 5 \).
By working through these problems, you will gain a deeper understanding of how the square root of 5 is applied in algebra.

Square Root of 5 in Geometry
The square root of 5, denoted as \( \sqrt{5} \), has various geometric interpretations and constructions. One of the classical methods to construct \( \sqrt{5} \) involves using a right triangle and the Pythagorean theorem.
To geometrically construct \( \sqrt{5} \) using a right triangle:
- Start with a line segment AB of length 2 units.
- At point B, construct a perpendicular line segment BC of length 1 unit.
- Connect points A and C to form the hypotenuse AC of the right triangle ABC.
- According to the Pythagorean theorem: \( AC = \sqrt{AB^2 + BC^2} \).
Since \( AB = 2 \) and \( BC = 1 \), we have:
\[
AC = \sqrt{2^2 + 1^2} = \sqrt{4 + 1} = \sqrt{5}
\]
This construction shows that the length of the hypotenuse AC in a right triangle with legs of lengths 2 and 1 is \( \sqrt{5} \).
Another method involves using a semicircle and the geometric mean:
- Draw a line segment AB of length 1 unit.
- Extend the line segment to point C, such that AC is 2 units.
- Find the midpoint M of segment AC.
- Draw a semicircle with center M and radius MA.
- From point B, draw a line perpendicular to AC intersecting the semicircle at point D.
By the properties of the circle and right triangles inscribed in semicircles:
\[
BD = \sqrt{AB \cdot BC}
\]
Since \( AB = 1 \) and \( BC = 4 \), we have:
\[
BD = \sqrt{1 \cdot 4} = \sqrt{4} = 2
\]
By adjusting the length of BC to 5, we get \( BD = \sqrt{5} \).
These geometric methods are useful for visualizing and constructing the square root of 5, demonstrating its significance in geometry.
Square Root of 5 in Number Theory
The square root of 5, denoted as \( \sqrt{5} \), plays a significant role in number theory. It is an irrational number, which means it cannot be expressed as a simple fraction and its decimal representation is non-repeating and non-terminating. Proving its irrationality can be achieved through a classic proof by contradiction.
Proof of Irrationality
Assume \( \sqrt{5} \) is rational, meaning it can be written as \( \frac{x}{y} \) where \( x \) and \( y \) are coprime integers (i.e., their greatest common divisor is 1). Squaring both sides gives:
\[ \sqrt{5} = \frac{x}{y} \implies 5 = \frac{x^2}{y^2} \implies 5y^2 = x^2 \]
This implies that \( x^2 \) is divisible by 5, so \( x \) must also be divisible by 5 (since 5 is a prime number). Let \( x = 5k \) for some integer \( k \). Substituting back gives:
\[ 5y^2 = (5k)^2 \implies 5y^2 = 25k^2 \implies y^2 = 5k^2 \]
This implies that \( y^2 \) is also divisible by 5, so \( y \) must also be divisible by 5. However, this contradicts the initial assumption that \( x \) and \( y \) are coprime. Therefore, \( \sqrt{5} \) cannot be rational and must be irrational.
Continued Fractions
The continued fraction representation of \( \sqrt{5} \) provides insight into its properties. It is expressed as:
\[ \sqrt{5} = [2; 4, 4, 4, \ldots] \]
This periodic continued fraction reflects the inherent structure and regularity within the irrational number.
Connections to Fibonacci and Lucas Numbers
Interestingly, \( \sqrt{5} \) is related to the Fibonacci and Lucas numbers. The ratio of successive Fibonacci numbers converges to the golden ratio \( \varphi \), and the relationship between the golden ratio and \( \sqrt{5} \) is given by:
\[ \varphi = \frac{1 + \sqrt{5}}{2} \]
This relationship can also be seen in the Lucas numbers, where the limit of the ratio of successive Lucas numbers equals \( \sqrt{5} \):
\[ \lim_{n \to \infty} \frac{L_n}{F_n} = \sqrt{5} \]
Diophantine Equations
In number theory, Diophantine equations often involve solutions where the square root of integers play a crucial role. For example, solutions to equations like:
\[ x^2 - 5y^2 = 1 \]
are closely related to Pell's equation, where \( \sqrt{5} \) appears as a fundamental solution. These equations and their solutions are significant in studying the properties of quadratic irrationals and the units of quadratic fields.
Conclusion
The square root of 5 is a fascinating number in number theory due to its irrational nature, its continued fraction representation, and its connection to the Fibonacci and Lucas numbers. It also plays a vital role in the solutions of various Diophantine equations, making it an essential topic in the study of number theory.
Importance of Irrational Numbers
Irrational numbers are crucial in mathematics and have significant implications in various fields. These numbers cannot be expressed as a simple fraction of two integers, and their decimal expansions are non-terminating and non-repeating. Examples include numbers like \(\pi\), \(e\), and the square roots of non-perfect squares, such as \(\sqrt{2}\) and \(\sqrt{5}\).
Here are some key points that highlight the importance of irrational numbers:
- Foundation of Real Numbers: Irrational numbers, along with rational numbers, form the set of real numbers. This comprehensive set is fundamental in various mathematical concepts, including calculus and analysis.
- Geometric Applications: Irrational numbers are vital in geometry. For example, the diagonal of a square with side length 1 is \(\sqrt{2}\), an irrational number. Similarly, the golden ratio, often encountered in geometry and art, is an irrational number.
- Trigonometry and Calculus: Many trigonometric functions and constants, such as \(\pi\) and \(e\), are irrational. These constants are essential in the study of waveforms, exponential growth and decay, and other phenomena described by calculus.
- Scientific Significance: Irrational numbers appear in scientific calculations and natural phenomena. For instance, \(\pi\) is crucial in calculations involving circles and spheres, while \(e\) is fundamental in describing growth processes in biology, economics, and other fields.
- Number Theory: Irrational numbers play a significant role in number theory. They help in understanding the distribution of prime numbers and the nature of different number sets.
The existence of irrational numbers demonstrates the complexity and richness of mathematics. Their non-repeating, non-terminating nature challenges our understanding of numbers and their representations, making them a fascinating area of study.
Understanding Non-repeating Decimals
Non-repeating decimals are decimal numbers that continue infinitely without any repeating pattern. These types of decimals are significant in mathematics as they often represent irrational numbers.
Here are some key characteristics and examples of non-repeating decimals:
- Definition: A non-repeating decimal is a decimal number that has an infinite number of digits after the decimal point and no repeating block of digits. This type of decimal cannot be represented as a fraction of two integers, which makes it an irrational number.
- Example 1: The decimal expansion of \(\pi\) (pi) is \(3.141592653589793...\), which continues indefinitely without repeating. This makes \(\pi\) an irrational number.
- Example 2: Euler's number \(e\) (approximately 2.71828...) is another example of a non-repeating decimal. Like \(\pi\), \(e\) continues without any repeating pattern and is an irrational number.
- Square Roots: Many square roots of non-perfect squares are non-repeating decimals. For instance, \(\sqrt{2}\) is approximately \(1.414213562...\), and \(\sqrt{5}\) is approximately \(2.236067977...\). Both of these values are non-repeating and therefore irrational.
Non-repeating decimals are crucial in understanding the concept of irrational numbers, which are numbers that cannot be expressed as the ratio of two integers. These numbers play a significant role in various fields of mathematics and real-world applications, including geometry, number theory, and calculus.
Below is a table summarizing some important non-repeating decimals:
| Number | Decimal Representation |
|---|---|
| \(\pi\) | 3.141592653589793... |
| \(e\) | 2.718281828459045... |
| \(\sqrt{2}\) | 1.414213562... |
| \(\sqrt{5}\) | 2.236067977... |
Understanding non-repeating decimals helps in recognizing the complexity and diversity of numbers, enriching our comprehension of mathematical principles and their applications.

Historical Context of Square Roots
The concept of square roots has a rich historical background, dating back to ancient civilizations. Early records of square roots can be traced to the Babylonians, who around 1800 BCE developed methods to approximate the square roots of numbers using a form of the method now known as the "Babylonian method" or "Heron's method".
The ancient Egyptians also engaged in mathematical calculations involving square roots, as evidenced by the Rhind Mathematical Papyrus (circa 1650 BCE), which contains a table of square roots.
In ancient Greece, mathematicians like Pythagoras and Euclid further explored square roots. Euclid's "Elements" includes propositions that indirectly involve the square root, laying foundational principles of geometry that depend on the concept.
The Indian mathematician Aryabhata in the 5th century provided algorithms for finding square roots, which were later expanded by Brahmagupta in the 7th century. These methods spread to the Islamic world, where scholars like Al-Khwarizmi further refined them.
In Europe, the Renaissance period saw significant advances in the understanding and computation of square roots. Notably, the German mathematician Christoff Rudolff introduced the radical symbol (√) in his work "Coss" (1525), which became the standard notation for square roots.
The development of modern algebra and calculus in the 17th and 18th centuries by mathematicians such as René Descartes, Isaac Newton, and Gottfried Wilhelm Leibniz provided more systematic methods for handling square roots and other irrational numbers.
Today, square roots are a fundamental aspect of mathematics, with applications spanning various fields such as engineering, physics, and computer science, reflecting the extensive history and continual development of this essential mathematical concept.
Căn Bậc Hai của 5 Được Đơn Giản Hóa
READ MORE:
Xem video để học cách biểu diễn căn bậc hai của 5 trên đường số một cách dễ dàng và chính xác.
Hiển thị cách căn bậc hai của 5 có thể được biểu diễn trên đường số | Định vị căn bậc hai của 5 trên đường số