Topic 9 square rooted: Discover the mathematical beauty and practical applications of the square root of 9. This introduction delves into the significance of finding the square root of numbers, particularly focusing on the number 9, and explores its usefulness in various mathematical contexts. Understand how the square root of 9 simplifies and how it plays a role in solving mathematical problems efficiently.
Table of Content
- Square Root of 9
- Introduction to Square Roots
- Understanding the Square Root of 9
- Mathematical Properties of Square Roots
- Methods for Calculating Square Roots
- Simplifying Square Roots
- Examples and Applications
- Using Square Root Calculators
- Perfect Squares and Their Properties
- Square Roots of Non-Perfect Squares
- Visual Representation of Square Roots
- YOUTUBE: Tìm hiểu cách tính căn bậc hai của số 9 và ứng dụng của nó trong toán học qua video này.
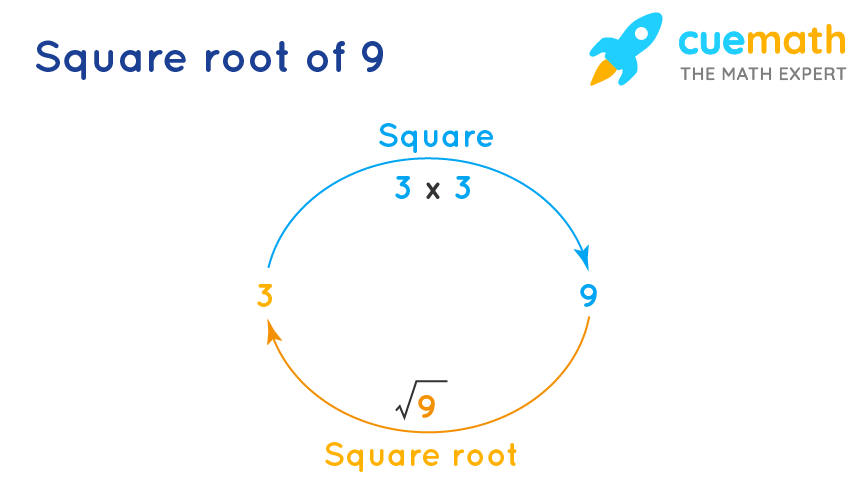
Square Root of 9
The square root of 9 is a commonly discussed mathematical topic. Below is a detailed overview of this concept.
Definition
The square root of a number is a value that, when multiplied by itself, gives the original number. For 9, the square root is:
\(\sqrt{9} = \pm 3\)
This means that both 3 and -3 are square roots of 9 because:
- \(3^2 = 9\)
- \((-3)^2 = 9\)
Methods to Find Square Roots
-
Trial and Error
Guess a number, square it, and see if the result matches the original number. Adjust your guess accordingly.
-
Using Calculators
Online calculators like Mathway and CalculatorSoup can quickly compute square roots.
-
Long Division Method
Useful for non-perfect squares but can also be applied to perfect squares for verification.
Applications of Square Roots
Square roots are used in various fields including geometry, algebra, and real-world problem-solving to find dimensions, roots of equations, and in statistical calculations.
Example Problems
| Expression | Result |
| \(\sqrt{81}\) | \(\pm 9\) |
| \(\sqrt{25}\) | \(\pm 5\) |
| \(\sqrt{100}\) | \(\pm 10\) |
Interesting Facts
- Every positive number has two square roots: one positive and one negative.
- The square root symbol (\(\sqrt{}\)) is also known as the radical sign.
- The square root of 9 is a rational number because it can be expressed as 3/1.
Understanding the square root of 9 helps build foundational knowledge for more advanced mathematical concepts.

READ MORE:
Introduction to Square Roots
The concept of square roots is fundamental in mathematics. A square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 9 is 3 because \(3 \times 3 = 9\). This section will provide a detailed introduction to square roots, including their properties, examples, and methods for calculating them.
Mathematically, the square root of a number \(x\) is represented as \(\sqrt{x}\). The square root function maps the number \(x\) to a non-negative value \(y\) such that \(y^2 = x\).
Properties of Square Roots
- The square root of a positive number has two values: one positive and one negative. For example, the square roots of 9 are 3 and -3 because both \(3 \times 3\) and \(-3 \times -3\) equal 9.
- The square root of 0 is 0.
- Square roots of negative numbers are not real numbers. They are represented using imaginary numbers, for instance, \(\sqrt{-1} = i\).
Perfect Squares
Perfect squares are numbers whose square roots are integers. Here are some examples:
| Number | Square Root |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
Calculating Square Roots
Finding the square root of a perfect square is straightforward. However, finding the square root of non-perfect squares can be more challenging. Here are some methods:
- Estimation: For numbers that are not perfect squares, you can estimate the square root by finding the nearest perfect squares. For example, the square root of 10 is between 3 (since \(3^2 = 9\)) and 4 (since \(4^2 = 16\)).
- Using a calculator: The most accurate and quickest way to find a square root is by using a calculator.
- Long division method: This manual method involves a process similar to long division and is useful for finding square roots without a calculator.
Understanding square roots is crucial as they appear in various mathematical contexts, including algebra, geometry, and calculus. Mastery of square roots will greatly aid in solving equations and understanding mathematical relationships.
Understanding the Square Root of 9
The square root of a number is a value that, when multiplied by itself, gives the original number. In the case of 9, the square root is 3 because \( 3 \times 3 = 9 \). This makes 3 the principal square root of 9, often denoted as \( \sqrt{9} = 3 \). However, it's important to note that -3 is also a square root of 9 since \( (-3) \times (-3) = 9 \).
To further understand the concept of square roots, let's break it down into steps:
- Definition: The square root of a number \( x \) is a number \( y \) such that \( y^2 = x \). For positive \( x \), the principal square root is positive.
- Principal and Negative Roots: Every positive number has two square roots: one positive (principal root) and one negative. For example, the square roots of 9 are \( +3 \) and \( -3 \).
- Perfect Squares: Numbers like 1, 4, 9, 16, 25, etc., are perfect squares because their square roots are integers.
- Calculating Square Roots: The square root can be calculated using a calculator or estimated by finding two perfect squares it lies between. For instance, since \( 3^2 = 9 \) and \( 2^2 = 4 \), the square root of 9 is exactly 3.
Here is a table summarizing some common perfect squares and their square roots:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
In summary, the principal square root of 9 is 3, but remember that the negative root, -3, is also valid. Understanding these basics helps in various mathematical computations and problem-solving scenarios.
Mathematical Properties of Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. Square roots have several important mathematical properties, which are useful in various areas of mathematics including algebra, calculus, and number theory. Here, we will explore some of these properties in detail.
- Principal Square Root: Every non-negative real number \(a\) has a unique non-negative square root, known as the principal square root, denoted by \(\sqrt{a}\). For example, \(\sqrt{9} = 3\).
- Positive and Negative Roots: While the principal square root is non-negative, every positive number actually has two square roots: a positive and a negative. For instance, \(\sqrt{9} = 3\) and \(-\sqrt{9} = -3\), since both \(3^2\) and \((-3)^2\) equal 9.
- Properties of Radicals: Square roots follow certain algebraic rules:
- \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\)
- \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\)
- \((\sqrt{a})^2 = a\)
- Perfect Squares: A number that is the square of an integer is called a perfect square. The square root of a perfect square is always an integer. Examples include 1, 4, 9, 16, and 25.
- Irrational Numbers: The square root of a non-perfect square is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation is non-terminating and non-repeating. For example, \(\sqrt{2} \approx 1.41421\).
- Square Root Function: The square root function \(f(x) = \sqrt{x}\) is defined for all non-negative real numbers \(x\). It is an increasing function, meaning that as \(x\) increases, \(\sqrt{x}\) also increases.
Understanding these properties of square roots helps in simplifying radical expressions, solving equations, and analyzing functions. Square roots are fundamental in various mathematical contexts, and mastering their properties provides a strong foundation for further mathematical learning.
Methods for Calculating Square Roots
Calculating square roots can be done through several methods, each with varying levels of complexity and precision. Here are some common methods:
-
Prime Factorization Method
This method involves breaking down the number into its prime factors and then pairing the factors to find the square root.
- Example: To find the square root of 36, break it down into prime factors: 36 = 2 × 2 × 3 × 3. Pair the factors (2 × 3) and multiply: √36 = 2 × 3 = 6.
-
Estimation and Approximation
This method is useful for numbers that are not perfect squares. It involves finding the two closest perfect squares the number lies between and estimating the square root.
- Example: To estimate √10, note that 32 = 9 and 42 = 16. Therefore, √10 is between 3 and 4. Refine the estimate by trying values like 3.1, 3.2, etc.
-
Long Division Method
This method is similar to the long division process and is used to find more precise square roots.
- Step-by-step:
- Group the digits into pairs, starting from the decimal point.
- Find the largest number whose square is less than or equal to the first group. Write this number as the divisor and quotient.
- Subtract the square of the quotient from the first group and bring down the next pair of digits.
- Double the quotient and find the next digit of the quotient that, when used in the new divisor, gives a product less than or equal to the current number.
- Repeat the process for the desired precision.
- Step-by-step:
-
Using a Calculator
The simplest and quickest method is to use a calculator. Most calculators have a square root button (√) that provides an instant result.
- Example: Enter 25 and press the √ button to get 5.
-
Newton's Method (Iterative Approach)
Newton's method provides a systematic way to approximate square roots. It involves iterative calculation using an initial guess.
- Example: To find √10:
- Start with an initial guess, say 3.
- Apply the formula: \( \text{New guess} = \frac{1}{2} \left( \text{Old guess} + \frac{\text{Number}}{\text{Old guess}} \right) \)
- Repeat the iteration until the guess is accurate enough.
- Example: To find √10:
Each method has its own applications and levels of accuracy. For most everyday purposes, a calculator or estimation method suffices, but for precise calculations, methods like long division or Newton's iterative approach are recommended.
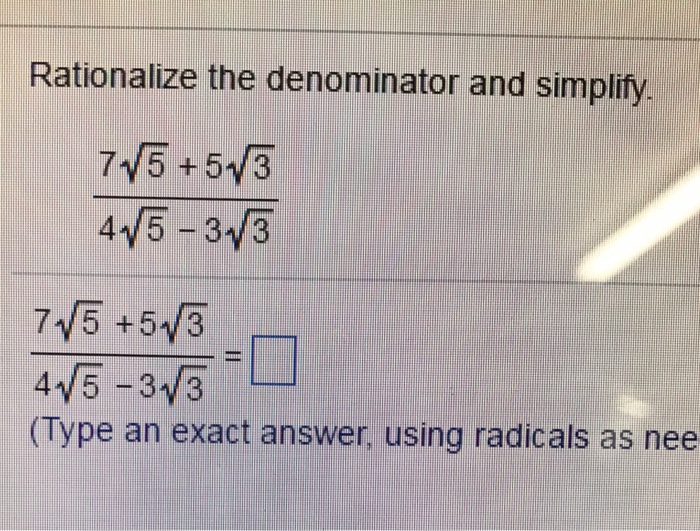
Simplifying Square Roots
To simplify a square root, the goal is to express the number inside the square root as a product of smaller numbers, one of which is a perfect square. This process reduces the square root to its simplest form.
Step-by-Step Simplification
- Factor the number under the square root into its prime factors.
- Identify pairs of prime factors.
- Move one number from each pair outside the square root.
- Multiply the numbers outside the square root together.
- Multiply the remaining numbers inside the square root together.
Here is the rule to remember:
\[\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b}\]
Examples
- Simplifying \(\sqrt{12}\)
12 is 4 times 3, so:
\[\sqrt{12} = \sqrt{4 \cdot 3} = \sqrt{4} \cdot \sqrt{3} = 2\sqrt{3}\]
- Simplifying \(\sqrt{45}\)
45 is 9 times 5, so:
\[\sqrt{45} = \sqrt{9 \cdot 5} = \sqrt{9} \cdot \sqrt{5} = 3\sqrt{5}\]
- Simplifying \(\sqrt{18}\)
18 is 9 times 2, so:
\[\sqrt{18} = \sqrt{9 \cdot 2} = \sqrt{9} \cdot \sqrt{2} = 3\sqrt{2}\]
Using Fractions
Similar rules apply for fractions:
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
Example:
\[\sqrt{\frac{30}{10}} = \sqrt{3}\]
More Complex Examples
- Simplifying \(\sqrt{20} \cdot \sqrt{5} \cdot \sqrt{2}\)
First combine under one square root:
\[\sqrt{20 \cdot 5 \cdot 2} = \sqrt{200} = \sqrt{100 \cdot 2} = 10\sqrt{2}\]
- Simplifying \(2\sqrt{12} + 9\sqrt{3}\)
First simplify \(2\sqrt{12}\):
\[2\sqrt{12} = 2 \cdot 2\sqrt{3} = 4\sqrt{3}\]
Then add like terms:
\[4\sqrt{3} + 9\sqrt{3} = (4+9)\sqrt{3} = 13\sqrt{3}\]
Surds
Note: A root that cannot be simplified further is called a surd. For example, \(\sqrt{3}\) is a surd, while \(\sqrt{4} = 2\) is not.
Examples and Applications
The concept of square roots is widely used in various fields such as mathematics, engineering, and physics. Here, we explore some practical examples and applications of square roots.
- Geometry: The square root is used to determine the side length of a square given its area. For instance, if the area of a square is 9 square units, the side length is the square root of 9, which is 3 units.
- Algebra: Square roots are essential in solving quadratic equations. For example, the solutions to \(x^2 = 9\) are \(x = \pm3\).
- Engineering: In engineering, square roots are used in calculations involving areas and volumes. For example, in civil engineering, the square root can help determine the size of materials needed for construction projects.
- Physics: In physics, square roots are used in formulas to calculate various properties such as the root mean square velocity in kinetic theory and the standard deviation in statistics.
- Finance: In finance, the square root is used in the calculation of volatility and standard deviation of returns, which are essential for risk assessment and portfolio management.
Overall, the square root is a fundamental mathematical tool with diverse applications across many disciplines.
Using Square Root Calculators
Square root calculators are useful tools for quickly finding the square root of any number, including the square root of 9. These calculators can be found online or as part of mathematical software and apps. Here's a step-by-step guide on how to use a square root calculator:
- Access the Calculator:
Open your web browser and navigate to an online square root calculator. You can also use a calculator app on your smartphone or a physical calculator with a square root function.
- Enter the Number:
Input the number you want to find the square root of into the calculator. For example, to find the square root of 9, you would enter '9' in the input field.
- Calculate the Square Root:
Press the square root button, often denoted as √ or a button labeled 'sqrt'. The calculator will then display the result.
- Interpret the Result:
The calculator will show the square root of the entered number. For instance, if you entered 9, the display will show 3, because the square root of 9 is 3.
Here is a simple example using MathJax to represent the calculation:
\[
\sqrt{9} = 3
\]
Square root calculators can also handle more complex calculations, such as finding the square roots of non-perfect squares or dealing with decimal numbers. Some advanced calculators can show the process of simplification, offer multiple roots (for non-real numbers), and provide additional mathematical functions.
Below is a summary table of common square roots for reference:
| Number | Square Root |
|---|---|
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
By following these steps, you can effectively use a square root calculator to find the square root of any number, enhancing your understanding and solving mathematical problems efficiently.
Perfect Squares and Their Properties
Perfect squares are numbers that are the product of an integer multiplied by itself. They have unique properties and play a significant role in various mathematical concepts. Understanding perfect squares is essential for simplifying square roots and solving quadratic equations.
Definition of Perfect Squares
A perfect square is a number that can be expressed as the square of an integer. For example, \( 9 \) is a perfect square because it can be written as \( 3^2 \).
Mathematically, a number \( n \) is a perfect square if there exists an integer \( m \) such that \( n = m^2 \).
Examples of Perfect Squares
- \( 1 = 1^2 \)
- \( 4 = 2^2 \)
- \( 9 = 3^2 \)
- \( 16 = 4^2 \)
- \( 25 = 5^2 \)
- \( 36 = 6^2 \)
- \( 49 = 7^2 \)
- \( 64 = 8^2 \)
- \( 81 = 9^2 \)
- \( 100 = 10^2 \)
Properties of Perfect Squares
- Perfect squares end with specific digits: 0, 1, 4, 5, 6, or 9. For example, \( 49 \) ends in 9, \( 64 \) ends in 4.
- The square root of a perfect square is always an integer. For example, \( \sqrt{25} = 5 \).
- When represented in binary, the number of 1's in the binary representation of a perfect square is odd.
- The difference between consecutive perfect squares follows the pattern: \( (n+1)^2 - n^2 = 2n + 1 \). For example, \( 4 - 1 = 3 \), \( 9 - 4 = 5 \).
Visual Representation of Perfect Squares
Perfect squares can be visualized as square arrays of dots. For instance:
- \( 1 = 1 \times 1 \):
- \( 4 = 2 \times 2 \):
- \( 9 = 3 \times 3 \):
Applications of Perfect Squares
Perfect squares are used in various mathematical calculations and real-world applications:
- Simplifying Radicals: Perfect squares make it easier to simplify square root expressions. For instance, \( \sqrt{36} = 6 \).
- Geometry: Perfect squares are used in area calculations for squares. For example, the area of a square with side length 5 is \( 5^2 = 25 \).
- Algebra: Solving quadratic equations often involves working with perfect squares.
- Number Theory: Understanding properties of perfect squares helps in exploring number patterns and relationships.

Square Roots of Non-Perfect Squares
Square roots of non-perfect squares are numbers that do not have an integer as their square root. These numbers often result in irrational numbers, which cannot be expressed as a simple fraction and have non-repeating, non-terminating decimal parts.
To find the square root of a non-perfect square, follow these steps:
- Identify the number: Let’s take an example of a non-perfect square number such as 20.
- Estimate the square root: Find two perfect squares between which the number lies. For 20, it lies between 16 (4²) and 25 (5²). Therefore, the square root of 20 is between 4 and 5.
-
Refine the estimate: Use a method like the average method or a calculator to get a more accurate value. For example, a rough estimate using average:
- \((4 + 5) / 2 = 4.5\)
- \(4.5^2 = 20.25\), which is close to 20
- Further refine: \((4.4 + 4.5) / 2 = 4.45\)
- \(4.45^2 = 19.8025\), getting closer
- Use a calculator: For more precision, use a square root calculator. Enter the number and compute to get the result. For 20, it would be approximately 4.472.
Here’s a list of square roots of some common non-perfect squares:
| Number | Square Root |
|---|---|
| 2 | 1.414 |
| 3 | 1.732 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 10 | 3.162 |
It’s important to note that while the principal square root is positive, every nonnegative real number also has a negative square root. For example, the square roots of 20 are approximately ±4.472.
Visual Representation of Square Roots
Visualizing square roots can help in understanding their properties and applications better. There are various methods to visually represent square roots:
Geometric Interpretation
One common method is to use a geometric approach. The square root of a number can be represented as the side length of a square with an area equal to that number.
For example, the square root of 9 can be visualized as the side length of a square with an area of 9 square units.
- Draw a square and divide it into smaller squares to count the total area.
- If the area is 9, the side length of the square is 3, since \(3 \times 3 = 9\).
Number Line Representation
Square roots can also be represented on a number line:
- Mark the point 0 on the number line.
- Locate the point 9 on the number line.
- The square root of 9 is the positive value 3 and the negative value -3.
- Mark these points on the number line to show \( \sqrt{9} = \pm 3 \).
Graphical Representation
Graphical methods involve plotting the square root function on a graph:
- Plot the function \( y = \sqrt{x} \) on a Cartesian plane.
- For \( x = 9 \), \( y = \sqrt{9} = 3 \).
- This point (9, 3) lies on the curve of the square root function.
Area Models
Using area models is another way to visualize square roots:
- Consider a rectangle where one side is known, and the area is given.
- For instance, if the area is 9 square units, and one side is 3 units, the other side must also be 3 units.
- Thus, \( \sqrt{9} = 3 \).
Interactive Tools and Calculators
There are many online tools and calculators that can help visualize square roots:
- Use a square root calculator to input different values and see their square roots represented graphically.
- Interactive tools can show step-by-step how to find and visualize square roots.
Understanding these visual methods can deepen your comprehension of square roots and their properties.
Tìm hiểu cách tính căn bậc hai của số 9 và ứng dụng của nó trong toán học qua video này.
Giá trị của Căn bậc hai của 9
READ MORE:
Khám phá cách đơn giản hóa căn bậc hai của số 9 và các phương pháp thực hiện qua video này.
Cách Đơn Giản Hóa Căn Bậc Hai của 9: sqrt(9)