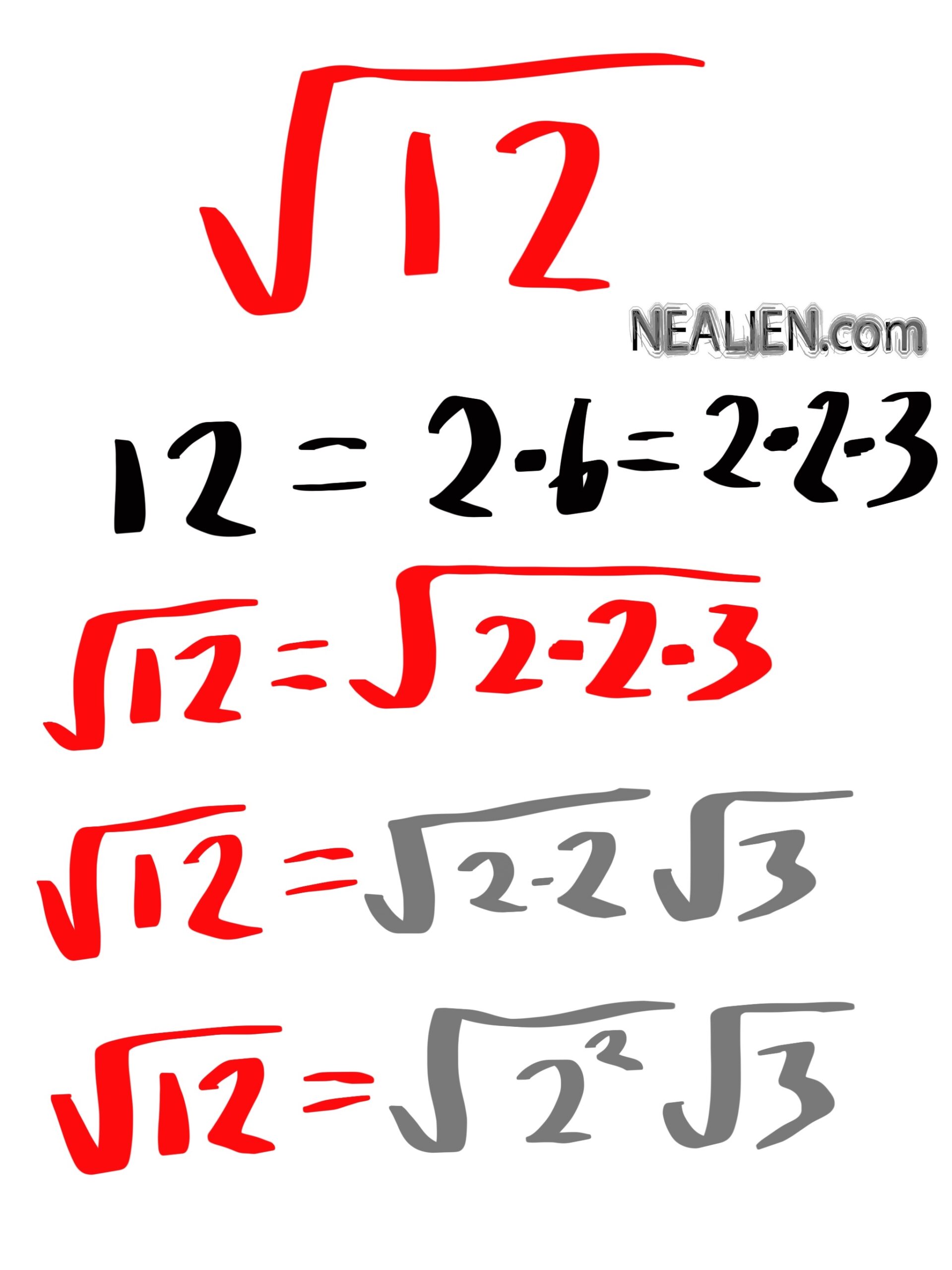Square Root 56 Simplified: Easy Steps to Simplify √56

The square root of 56 can be simplified by identifying and extracting the largest perfect square factor from under the square root symbol.

Steps to Simplify √56:

1. Find the prime factorization of 56:
   • 56 = 2 × 28
   • 28 = 2 × 14
   • 14 = 2 × 7
   • So, 56 = 2³ × 7
2. Identify the largest perfect square factor of 56:
   • The perfect square factors are 1 and 4 (since 2² = 4).
   • The largest perfect square factor of 56 is 4.
3. Rewrite 56 as the product of the largest perfect square factor and another number:
   • 56 = 4 × 14
4. Simplify the square root:
   • √56 = √(4 × 14)
   • Use the property of square roots: √(a × b) = √a × √b
   • √56 = √4 × √14
   • √4 = 2
   • Thus, √56 = 2√14

Therefore, the simplified form of √56 is 2√14.

Verification

To verify, you can square the simplified result and check if it equals the original number:

(2√14)² = 2² × (√14)² = 4 × 14 = 56

The simplification is correct.

Understanding how to simplify the square root of 56 is an essential skill in mathematics. This guide will provide a step-by-step explanation using the prime factorization method, ensuring you grasp the concept thoroughly. Whether you are a student, educator, or math enthusiast, this article aims to make the process clear and accessible. Let's delve into the fundamentals and simplify √56 together.

1. What is a Square Root?

   The square root of a number is a value that, when multiplied by itself, gives the original number. For instance, the square root of 25 is 5 because \(5 \times 5 = 25\).

2. Introduction to Simplifying Square Roots

   Simplifying a square root involves breaking down the number inside the root into its prime factors and then simplifying further if possible. This helps in expressing the square root in its simplest form.

3. Example: Simplifying the Square Root of 56

   We will use the prime factorization method to simplify √56. Follow along as we demonstrate this step-by-step.

By the end of this section, you will be equipped with the knowledge and skills needed to simplify square roots effectively. Let's get started!

The concept of square roots is fundamental in mathematics and plays a crucial role in various applications. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because \(3 \times 3 = 9\).

Here, we will explore the basics of square roots and their properties.

1. Definition of Square Root

   If \(x^2 = a\), then \(x\) is a square root of \(a\). This can be written as \(x = \sqrt{a}\). For instance, \(\sqrt{25} = 5\) because \(5^2 = 25\).

2. Properties of Square Roots
   • Non-negative Values: Square roots of non-negative numbers are non-negative. For instance, \(\sqrt{4} = 2\) and not -2.
   • Product Property: The square root of a product is the product of the square roots. For example, \(\sqrt{ab} = \sqrt{a} \times \sqrt{b}\).
   • Quotient Property: The square root of a quotient is the quotient of the square roots. For example, \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\) where \(b \neq 0\).
3. Special Square Roots

   Some numbers have square roots that are whole numbers, known as perfect squares. Examples include:

   • \(\sqrt{1} = 1\)
   • \(\sqrt{4} = 2\)
   • \(\sqrt{9} = 3\)
   • \(\sqrt{16} = 4\)
   • \(\sqrt{25} = 5\)
4. Simplifying Non-Perfect Square Roots

   To simplify square roots that are not perfect squares, we use methods such as prime factorization and identifying perfect square factors, which we will cover in the next sections.

With these fundamental concepts in mind, we can now move on to the specific techniques for simplifying the square root of 56.

Prime factorization is a method used to simplify square roots by breaking down the number into its prime factors. This method is particularly useful for simplifying the square root of 56. Follow the steps below to understand and apply the prime factorization method:

1. Identify the Prime Factors

   Start by dividing the number by the smallest prime number and continue dividing until all factors are prime.

   • 56 is an even number, so it is divisible by 2: \(56 \div 2 = 28\).
   • 28 is also even, so divide by 2 again: \(28 \div 2 = 14\).
   • 14 is even, so divide by 2 once more: \(14 \div 2 = 7\).
   • 7 is a prime number and cannot be divided further.

   Thus, the prime factors of 56 are \(2 \times 2 \times 2 \times 7\) or \(2^3 \times 7\).

2. Group the Prime Factors

   Next, pair the prime factors to simplify the square root. Since square roots are based on pairs of numbers, look for pairs in the prime factorization:

   • The prime factors of 56: \(2^3 \times 7\).
   • Pair the 2s: \(2^2 \times 2 \times 7\).
3. Extract the Pairs

   For each pair of prime factors, take one factor out of the square root:

   • \(\sqrt{2^2 \times 2 \times 7} = \sqrt{2^2} \times \sqrt{2 \times 7}\).
   • Simplify the pairs: \(2 \times \sqrt{14}\).

   Thus, the simplified form of \(\sqrt{56}\) is \(2\sqrt{14}\).

By using the prime factorization method, you can simplify the square root of 56 to \(2\sqrt{14}\). This method can be applied to other numbers to simplify their square roots as well.

Identifying perfect square factors is an essential step in simplifying square roots. Perfect square factors are numbers that are the square of an integer. By recognizing these factors, you can simplify the square root more efficiently. Here’s a step-by-step guide to identifying perfect square factors for simplifying the square root of 56:

1. Understand Perfect Squares

   A perfect square is a number that can be expressed as the product of an integer with itself. Examples include 1, 4, 9, 16, 25, etc.

2. List the Factors of the Number

   Identify all the factors of the number whose square root you are simplifying. For 56, the factors are:

   • 1
   • 2
   • 4
   • 7
   • 8
   • 14
   • 28
   • 56
3. Identify the Perfect Square Factors

   From the list of factors, identify which ones are perfect squares. For 56, the perfect square factors are:

   • 1 (\(1^2\))
   • 4 (\(2^2\))
4. Simplify the Square Root

   Use the largest perfect square factor to simplify the square root. For \(\sqrt{56}\), the largest perfect square factor is 4.

   • Write 56 as the product of 4 and another number: \(56 = 4 \times 14\).
   • Simplify \(\sqrt{56}\) using the perfect square factor: \(\sqrt{56} = \sqrt{4 \times 14}\).
   • Since \(\sqrt{4} = 2\), this can be simplified to: \(\sqrt{4} \times \sqrt{14} = 2\sqrt{14}\).

By identifying and using perfect square factors, you can simplify the square root of 56 to \(2\sqrt{14}\). This approach helps in breaking down complex square roots into simpler forms.

Simplifying the square root of 56 involves breaking it down into its prime factors and then using perfect square factors to simplify further. Here is a step-by-step guide to the simplification process:

1. Prime Factorization

   Start by finding the prime factors of 56:

   • 56 is divisible by 2: \(56 \div 2 = 28\).
   • 28 is divisible by 2: \(28 \div 2 = 14\).
   • 14 is divisible by 2: \(14 \div 2 = 7\).
   • 7 is a prime number.

   So, the prime factorization of 56 is \(2^3 \times 7\).

2. Identifying Perfect Square Factors

   Next, identify any perfect square factors within the prime factorization:

   • The prime factors of 56 are \(2^3 \times 7\).
   • We can rewrite \(2^3\) as \(2^2 \times 2\).
   • So, \(56 = 2^2 \times 2 \times 7\).
   • The perfect square factor here is \(2^2 = 4\).
3. Simplifying the Square Root

   Now, simplify the square root using the perfect square factor:

   • \(\sqrt{56} = \sqrt{2^2 \times 2 \times 7}\).
   • Separate the perfect square factor: \(\sqrt{2^2} \times \sqrt{2 \times 7}\).
   • Simplify \(\sqrt{2^2}\) to 2: \(2 \times \sqrt{14}\).

   Thus, the simplified form of \(\sqrt{56}\) is \(2\sqrt{14}\).

By following these steps, you can easily simplify the square root of 56 to \(2\sqrt{14}\). This method can be applied to simplify other square roots as well.

After simplifying the square root of 56 to \(2\sqrt{14}\), it is important to verify the correctness of this simplified form. Here is a step-by-step process to verify the simplified form:

1. Calculate the Original Square Root

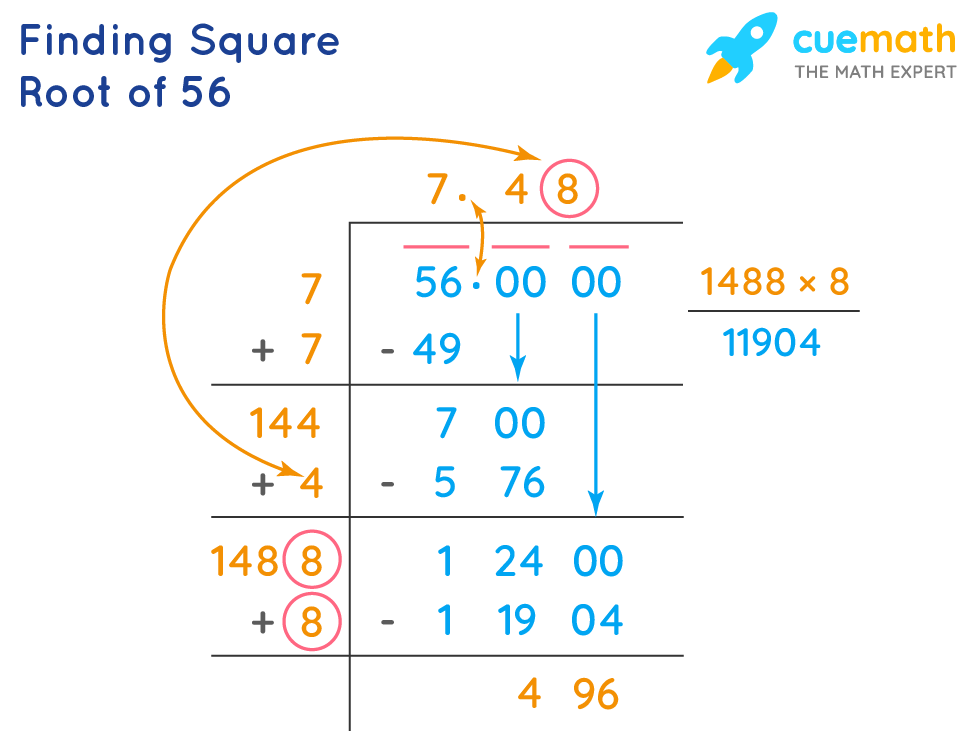
   First, calculate the square root of 56 using a calculator to get a decimal approximation:

   • \(\sqrt{56} \approx 7.4833\).
2. Calculate the Simplified Form

   Next, calculate \(2\sqrt{14}\) to ensure it matches the original square root:

   • Find the square root of 14: \(\sqrt{14} \approx 3.7417\).
   • Multiply by 2: \(2 \times 3.7417 \approx 7.4834\).
3. Compare the Results

   Compare the decimal approximations to verify they are equal:

   • Original square root: \(\sqrt{56} \approx 7.4833\).
   • Simplified form: \(2\sqrt{14} \approx 7.4834\).

   Both results are very close, confirming that the simplified form \(2\sqrt{14}\) is accurate.

By following this verification process, you can be confident that the simplified form of the square root of 56, \(2\sqrt{14}\), is correct. This verification method can be used for other square roots to ensure accuracy.

Simplifying square roots can sometimes lead to errors if not done carefully. Here are some common mistakes to avoid when simplifying the square root of 56 and other numbers:

1. Incorrect Prime Factorization

   Ensure that you correctly identify the prime factors of the number. A mistake in the prime factorization can lead to an incorrect simplification.

   • For example, the prime factors of 56 are \(2^3 \times 7\). Misidentifying these factors will result in errors in the simplification process.
2. Forgetting to Pair Prime Factors

   When simplifying, remember to look for pairs of prime factors. Only paired factors can be taken out of the square root.

   • For instance, in \(2^3 \times 7\), you can take out \(2^2\) as 2, but the remaining 2 and 7 stay inside the square root.
3. Not Identifying Perfect Square Factors

   Always identify the largest perfect square factor to simplify the square root efficiently.

   • In the case of 56, the perfect square factor is 4 (\(2^2\)), which simplifies to 2 outside the square root.
4. Incorrect Simplification

   After factoring, ensure you correctly simplify the expression. Missteps in arithmetic can lead to the wrong result.

   • For example, \(\sqrt{56} = \sqrt{4 \times 14} = 2\sqrt{14}\), not \(4\sqrt{14}\).
5. Verification

   Always verify your simplified form by calculating the decimal approximations to ensure they match the original value.

   • \(\sqrt{56} \approx 7.4833\) should match \(2\sqrt{14} \approx 7.4834\).

By being aware of these common mistakes and taking care to avoid them, you can accurately simplify square roots and strengthen your understanding of this important mathematical concept.

Square roots are not just theoretical concepts; they have numerous practical applications in various fields. Understanding how to simplify and use square roots is essential in real-world situations. Here are some practical applications:

1. Geometry and Trigonometry

   Square roots are used to calculate distances, areas, and volumes in geometric shapes. For example:

   • Pythagorean Theorem: In a right-angled triangle, the length of the hypotenuse is found using \(\sqrt{a^2 + b^2}\).
   • Circle Area: The radius of a circle can be derived from the area \(A = \pi r^2\) using \(r = \sqrt{\frac{A}{\pi}}\).
2. Physics

   Square roots are used to solve problems involving speed, acceleration, and energy. For instance:

   • Velocity: The root-mean-square velocity of gas molecules is given by \(v_{rms} = \sqrt{\frac{3kT}{m}}\).
   • Kinetic Energy: The energy of an object is \(KE = \frac{1}{2}mv^2\), and velocity can be derived using \(v = \sqrt{\frac{2KE}{m}}\).
3. Engineering

   Engineers use square roots in various calculations, including stress analysis and electrical engineering:

   • Structural Analysis: Calculating the natural frequency of a structure involves square roots, \(f_n = \frac{1}{2\pi}\sqrt{\frac{k}{m}}\).
   • Ohm's Law: In AC circuits, impedance \(Z = \sqrt{R^2 + (XL - XC)^2}\) involves square roots.
4. Statistics

   Square roots are crucial in statistical formulas and probability:

   • Standard Deviation: A measure of data dispersion is given by \(\sigma = \sqrt{\frac{\sum (x_i - \mu)^2}{N}}\).
   • Regression Analysis: The correlation coefficient involves square root calculations.
5. Finance

   Square roots are used in financial models to assess risk and return:

   • Compound Interest: The future value of investments involves calculations with square roots.
   • Volatility: Standard deviation in finance is a measure of asset price volatility.

These examples demonstrate the importance of square roots in various disciplines. Mastering square roots and their simplifications can enhance problem-solving skills in academic and professional settings.

Understanding square roots can sometimes be challenging. Here are some frequently asked questions that might help clarify any doubts:

• What is a square root?

  A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 56 is a number that when squared equals 56.

• How do you find the square root of 56?

  To find the square root of 56, you can use the prime factorization method or a calculator. The prime factorization method involves breaking down 56 into its prime factors and simplifying.

• Can the square root of 56 be simplified?

  Yes, the square root of 56 can be simplified. By expressing 56 as the product of its prime factors, 56 = 2^3 * 7, and then simplifying, we get:

  \(\sqrt{56} = \sqrt{2^3 \times 7} = 2 \sqrt{14}\)

• Is \(\sqrt{56}\) a rational or irrational number?

  The square root of 56 is an irrational number because it cannot be expressed as a simple fraction and its decimal form is non-repeating and non-terminating.

• What are perfect squares?

  Perfect squares are numbers that are the square of an integer. For example, 1, 4, 9, 16, 25, and 36 are perfect squares because they are the squares of 1, 2, 3, 4, 5, and 6 respectively.

• How do you verify the simplified form of a square root?

  To verify the simplified form of a square root, you can square the simplified expression and check if you get the original number. For example:

  \((2 \sqrt{14})^2 = 4 \times 14 = 56\)

• Why is simplifying square roots useful?

  Simplifying square roots makes them easier to work with in mathematical calculations and helps in better understanding the properties of the number.

• Are there any tools to help with square roots?

  Yes, there are various tools available such as scientific calculators, online calculators, and mathematical software that can help find and simplify square roots.

• What are some practical applications of square roots?

  Square roots are used in various fields including geometry (calculating the side length of a square given its area), physics (solving equations involving acceleration and distance), and finance (calculating standard deviation in statistics).

The square root of 56, while not a perfect square, offers an intriguing glimpse into the world of irrational numbers and their properties. Simplifying the square root of 56 yields \( \sqrt{56} = 2\sqrt{14} \), which provides a cleaner, more manageable form for calculations and applications.

Understanding the square root of 56 involves several methods, including prime factorization, long division, and approximation techniques. Each method highlights different mathematical principles and offers valuable insights into the nature of square roots. For instance, through prime factorization, we break down 56 into its prime factors (2, 2, 2, and 7), leading us to the simplified form \( 2\sqrt{14} \).

Moreover, recognizing that 56 is not a perfect square underscores its classification as an irrational number. This means its decimal representation is non-repeating and non-terminating, a key characteristic that differentiates it from rational numbers.

In practical terms, the square root of 56 is approximately 7.48, a value useful in various scientific and engineering applications where precise calculations are essential. Tools such as calculators and computer software can quickly provide this approximation, facilitating ease of use in real-world scenarios.

By exploring the square root of 56, we've not only simplified a specific mathematical expression but also gained a deeper appreciation for the techniques and tools that make such simplifications possible. Whether through manual calculation or digital assistance, the process enriches our mathematical understanding and equips us with the skills to tackle similar problems with confidence.