Topic square root 42 simplified: The square root of 42 simplified reveals fascinating insights into its mathematical properties. Understanding how to break down and approximate √42 can enhance your grasp of square roots and their practical applications. Dive into this exploration of simplifying the square root of 42 and discover its significance in various mathematical contexts.
Table of Content
- Square Root of 42 Simplified
- Introduction to Square Root of 42
- Understanding Square Roots and Simplification
- Mathematical Simplification of √42
- Approximation of √42
- Uses and Applications of √42
- Visual Representation of √42
- Comparison with Other Square Roots
- Conclusion on Simplifying √42
- Frequently Asked Questions about √42
- YOUTUBE:
Square Root of 42 Simplified
The square root of 42 is an irrational number, which means it cannot be expressed exactly as a simple fraction. However, it can be simplified using prime factorization to understand its approximate value and relationship to simpler roots.
Prime Factorization of 42
To simplify the square root of 42, we first find the prime factorization of 42:
- 42 = 2 × 3 × 7
Simplifying the Square Root
The square root of a product can be expressed as the product of the square roots of the factors:
\(\sqrt{42} = \sqrt{2 \times 3 \times 7}\)
Further Simplification
Since none of the factors (2, 3, and 7) are perfect squares, the square root of 42 cannot be simplified further into simpler square roots:
\(\sqrt{42} \approx 6.48\)
Approximation
For practical purposes, the square root of 42 is approximately:
\(\sqrt{42} \approx 6.48\)
Conclusion
While the square root of 42 cannot be simplified into a neat fraction or further broken down, understanding its prime factorization helps in grasping its approximate value and relationship to other numbers.

READ MORE:
Introduction to Square Root of 42
The square root of 42 is a mathematical expression that represents a value which, when multiplied by itself, equals 42. This value is denoted as \( \sqrt{42} \). The concept of square roots is fundamental in mathematics, providing a basis for various calculations and problem-solving techniques. Let's explore the details and simplification process of \( \sqrt{42} \).
To begin with, it's important to understand the nature of the number 42:
- 42 is a composite number.
- It can be factored into prime numbers.
Prime factorization of 42 is:
\( 42 = 2 \times 3 \times 7 \)
Using this factorization, we can express the square root of 42:
\( \sqrt{42} = \sqrt{2 \times 3 \times 7} \)
Simplifying square roots involves breaking down the number into its prime factors and identifying any pairs of factors. However, in the case of 42, none of the prime factors are perfect squares, which means \( \sqrt{42} \) cannot be simplified further in terms of exact roots:
\( \sqrt{42} \approx 6.4807 \)
This value is irrational, meaning it cannot be expressed as a simple fraction, but it can be approximated for practical uses.
In summary, the square root of 42 provides an interesting look into the properties of numbers and the methods used to simplify and approximate roots in mathematics.
Understanding Square Roots and Simplification
A square root of a number is a value that, when multiplied by itself, yields the original number. The square root is denoted by the radical symbol \( \sqrt{} \). For instance, \( \sqrt{42} \) represents the number that, when squared, equals 42. Square roots are fundamental in various areas of mathematics, including algebra and geometry.
Simplifying square roots involves expressing the root in its simplest form. This process often requires breaking down the number under the square root into its prime factors and looking for pairs of factors. Here’s how you can simplify a square root step by step:
- Prime Factorization:
Break down the number inside the square root into its prime factors. For 42, the prime factorization is:
\( 42 = 2 \times 3 \times 7 \)
- Group the Factors:
Identify pairs of prime factors. Since 42 is composed of the prime numbers 2, 3, and 7, none of these factors form pairs:
- \( \sqrt{42} = \sqrt{2 \times 3 \times 7} \)
- Simplify the Square Root:
If there were pairs of factors, we could simplify by taking one factor out of the square root for each pair. However, since 42 does not have repeated prime factors, \( \sqrt{42} \) cannot be simplified further:
\( \sqrt{42} \approx 6.4807 \)
- Approximation:
For practical purposes, we often approximate square roots to a certain number of decimal places. The square root of 42 is approximately 6.48 when rounded to two decimal places.
Understanding the process of simplifying square roots helps in various mathematical applications, such as solving quadratic equations, working with geometric shapes, and analyzing data. Simplified roots are easier to work with and provide clearer insights into the properties of numbers.
Mathematical Simplification of √42
The process of simplifying the square root of 42, denoted as \( \sqrt{42} \), involves breaking down the number into its prime factors and then applying the properties of square roots. Here's a step-by-step guide to the mathematical simplification of \( \sqrt{42} \):
- Prime Factorization:
First, find the prime factors of 42. The prime factorization is:
\( 42 = 2 \times 3 \times 7 \)
- Express the Square Root:
Rewrite the square root of 42 using its prime factors:
\( \sqrt{42} = \sqrt{2 \times 3 \times 7} \)
- Identify Perfect Squares:
Check for any pairs of prime factors that can be simplified. A pair of identical factors can be taken out of the square root as a single factor. In this case, there are no pairs of prime factors in 42 (2, 3, and 7 are all unique).
- Since there are no perfect square factors, \( \sqrt{42} \) cannot be simplified further in exact terms.
- Approximation:
While \( \sqrt{42} \) cannot be simplified exactly, it can be approximated. Using a calculator or estimation methods, the approximate value of \( \sqrt{42} \) is:
\( \sqrt{42} \approx 6.4807 \)
- Usage in Calculations:
For most practical applications, the approximate value is used. For instance, in engineering, physics, and other sciences, \( \sqrt{42} \approx 6.48 \) is often sufficient.
In conclusion, the square root of 42 cannot be simplified to a more basic form using prime factorization due to the absence of perfect square factors. However, understanding its prime factors and approximate value is crucial for various mathematical and practical applications.
Approximation of √42
The square root of 42, denoted as \( \sqrt{42} \), is an irrational number, meaning it cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion. To work with this number in practical applications, we often approximate it. Here is a detailed approach to approximating \( \sqrt{42} \):
- Initial Estimation:
Identify two perfect squares between which 42 lies. These are 36 (since \( 6^2 = 36 \)) and 49 (since \( 7^2 = 49 \)). Therefore:
\( 6 < \sqrt{42} < 7 \)
- Refine the Approximation:
To get a more precise value, we can use the average method. Start with the midpoint of 6 and 7:
\( \text{Midpoint} = \frac{6 + 7}{2} = 6.5 \)
Square this midpoint to see how close it is to 42:
\( 6.5^2 = 42.25 \)
Since 42.25 is slightly greater than 42, we know \( \sqrt{42} \) is slightly less than 6.5.
- Further Refinement:
Adjust the midpoint for more accuracy. Try 6.4 and 6.45:
- \( 6.4^2 = 40.96 \) (too low)
- \( 6.45^2 = 41.6025 \) (closer, but still low)
Continue refining within the range until the desired precision is reached. For instance:
\( 6.48^2 = 41.9904 \)
\( 6.481^2 = 42.003361 \)
- Using a Calculator:
For exact calculations, using a scientific calculator will give the value:
\( \sqrt{42} \approx 6.4807407 \)
- Practical Approximation:
For most practical purposes, rounding to two decimal places is sufficient:
\( \sqrt{42} \approx 6.48 \)
Approximating \( \sqrt{42} \) is essential in various fields such as engineering, physics, and everyday problem-solving. This step-by-step method ensures accuracy and helps in understanding the nature of irrational numbers.
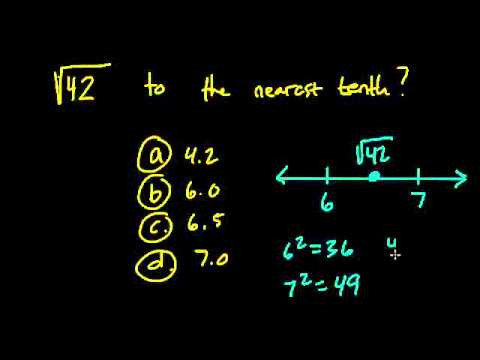
Uses and Applications of √42
The square root of 42, approximately 6.48, is a mathematical concept with several practical applications across various fields. Here are some key areas where √42 is utilized:
1. Geometry and Measurement
In geometry, the square root of 42 is used to calculate the side length of a square with an area of 42 square units. This application is essential in fields like architecture and construction, where accurate measurements are crucial for designing structures.
- Determining the side length of a square area of 42 square units: √42 ≈ 6.48 units
- Calculating the diagonal of a square with side lengths of 42 units using the Pythagorean theorem.
2. Engineering and Physics
√42 plays a role in various calculations and problem-solving scenarios in engineering and physics. For example:
- In electrical engineering, it can be used to determine the magnitude of alternating current (AC) or voltage in certain circuits.
- In physics, it's used in equations related to waveforms and oscillations, such as calculating the angular frequency and period of an oscillating system in simple harmonic motion.
3. Accident Investigation
Police use square roots to determine the speed of a car before applying brakes by measuring the length of skid marks. For instance, if the length of the skid marks is d feet, the speed of the car can be estimated using the formula:
speed ≈ √(24 * d) mphFor a car that leaves 190 feet of skid marks, the speed before braking can be calculated as:
speed ≈ √(24 * 190) ≈ 67.5 mph4. Area Calculations
When given the area of a square, the square root is used to find the length of each side. For instance:
| Area (square units) | Length of Side (units) |
|---|---|
| 9 | √9 = 3 |
| 144 | √144 = 12 |
| 42 | √42 ≈ 6.48 |
5. Free-fall Motion
In physics, the time it takes for an object to fall from a certain height can be calculated using the square root. For example, if an object is dropped from a height of h feet, the time in seconds to reach the ground is given by:
time = √(h) / 4For a height of 64 feet, the fall time would be:
time = √(64) / 4 = 8 / 4 = 2 secondsOverall, the square root of 42 is an invaluable tool in various practical applications, providing accurate measurements and aiding in problem-solving across different disciplines.
Visual Representation of √42
Visualizing the square root of 42 can be a fascinating way to understand its mathematical properties. Here are several methods to represent and understand √42 visually:
- Graphical Representation:
One way to represent √42 is through a number line. Plotting points for perfect squares close to 42, such as 36 (6²) and 49 (7²), helps to locate √42 between these values. By interpolating between 6 and 7, you can visually approximate √42 to be around 6.48.

- Geometric Squares:
Using square areas is another effective method. Draw a square with an area of 42 units². The side length of this square will be √42. While constructing such a square precisely can be challenging, it gives a visual approximation of the square root.

- Square Root Spiral:
A creative and intricate visual method is the square root spiral, where each step on the spiral represents the square root of successive integers. For √42, you would plot the 42nd step on the spiral, which visually represents its position relative to other square roots.

- Cartesian Plane:
On a Cartesian plane, plotting the function y = √x and identifying the point where x = 42 provides another visual understanding. This point's y-coordinate gives the value of √42.

Each of these methods provides a unique perspective on understanding and visualizing √42, helping to deepen the comprehension of square roots and their applications in various mathematical contexts.
Comparison with Other Square Roots
When comparing the square root of 42 with other square roots, it is useful to consider the values of other nearby numbers. Here is a detailed comparison:
- Square Root of 36 (√36):
- √36 = 6
- 36 is a perfect square, making its square root an integer.
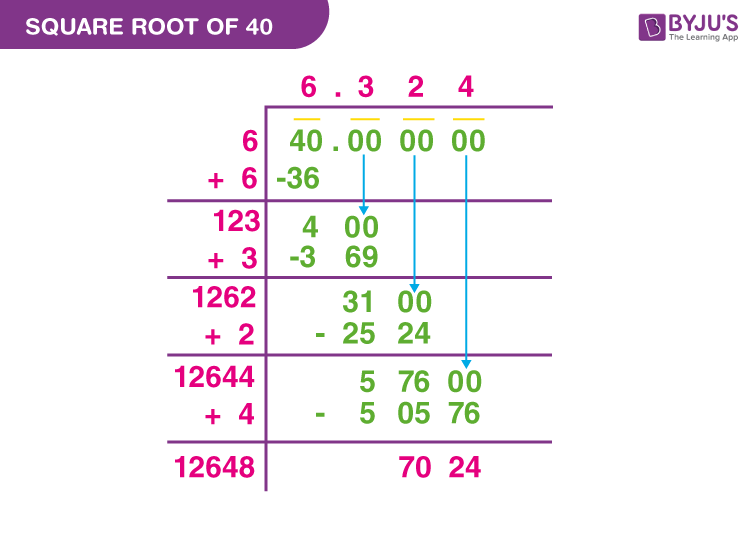
- Square Root of 40 (√40):
- √40 ≈ 6.3246
- 40 is not a perfect square, so its square root is an irrational number.
- Simplified form: √40 = 2√10
- Square Root of 42 (√42):
- √42 ≈ 6.4807
- 42 is not a perfect square, making its square root irrational.
- 42 has no perfect square factors, so it cannot be simplified further.
- Square Root of 49 (√49):
- √49 = 7
- 49 is a perfect square, resulting in an integer square root.
Here is a table comparing these square roots for easier visualization:
| Number | Square Root | Type | Simplified Form |
|---|---|---|---|
| 36 | 6 | Perfect Square | 6 |
| 40 | 6.3246 | Irrational | 2√10 |
| 42 | 6.4807 | Irrational | √42 |
| 49 | 7 | Perfect Square | 7 |
This comparison highlights how the square root of 42 fits within the context of other nearby square roots, demonstrating its properties and how it contrasts with both perfect squares and other non-perfect squares.
Conclusion on Simplifying √42
The square root of 42, denoted as √42, is an irrational number that cannot be simplified into a smaller radical form. This conclusion is drawn based on its prime factorization, which results in 2, 3, and 7 – none of which are perfect squares. Consequently, the square root of 42 remains in its radical form as √42.
For practical purposes, the approximate decimal value of √42 is widely used. By using methods such as long division, we find that √42 is approximately 6.4807. This approximation is helpful in various applications where an exact radical form is not required.
The process of understanding and simplifying square roots, even those that cannot be simplified further, is crucial in mathematics. It involves identifying prime factors and determining the presence of perfect squares. In the case of √42, this understanding reinforces the importance of approximation techniques and the acceptance of its radical form.
In conclusion, while the square root of 42 cannot be simplified into a simpler radical form, its decimal approximation provides a useful alternative for practical applications. The study of such numbers enhances our comprehension of irrational numbers and their properties within the broader context of mathematics.
Frequently Asked Questions about √42
Below are some frequently asked questions about the square root of 42, along with detailed answers.
- What is the square root of 42?
The square root of 42 is an irrational number, approximately equal to 6.4807.
- Is 42 a perfect square?
No, 42 is not a perfect square because it cannot be expressed as the square of an integer.
- Can the square root of 42 be simplified?
No, √42 cannot be simplified further because 42 does not have a square factor other than 1.
- What is the square root of 42 in exponential form?
The square root of 42 in exponential form is \(42^{1/2}\).
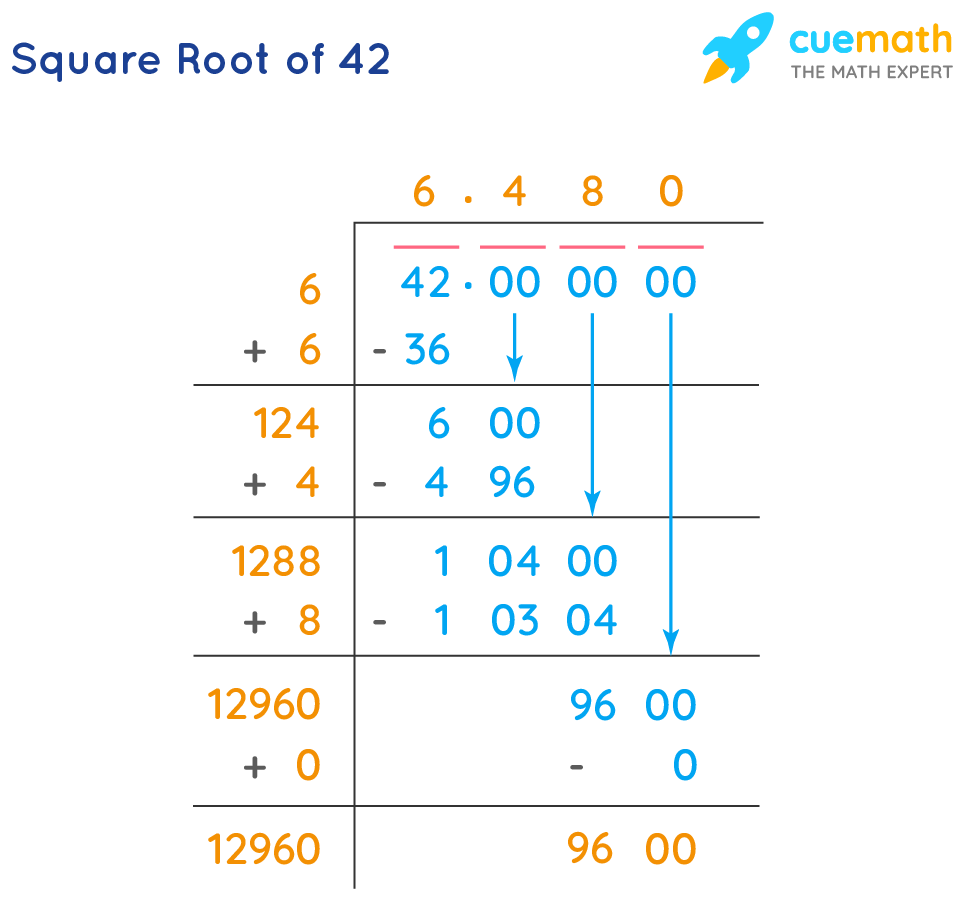
- How can the square root of 42 be calculated using long division?
The square root of 42 can be calculated using the long division method, which involves pairing the digits and finding a number that when multiplied by itself gives a value close to 42. This method yields a result of approximately 6.4807.
- What is the negative square root of 42?
The negative square root of 42 is approximately -6.4807.
- What is the square of 42?
The square of 42 is \(42^2 = 1764\).
- Is the square root of 42 rational or irrational?
The square root of 42 is an irrational number because it cannot be expressed as a simple fraction.
- How can the square root of 42 be calculated using a calculator?
To calculate the square root of 42 using a calculator, simply enter 42 and press the square root (√) button. The result will be approximately 6.4807.
Đơn giản hóa một phân số dưới dấu căn - Thủ thuật hợp pháp cho toán học
READ MORE:
09 - Đơn giản hóa căn bậc hai (Căn bậc hai) với phép nhân và chia, Phần 1