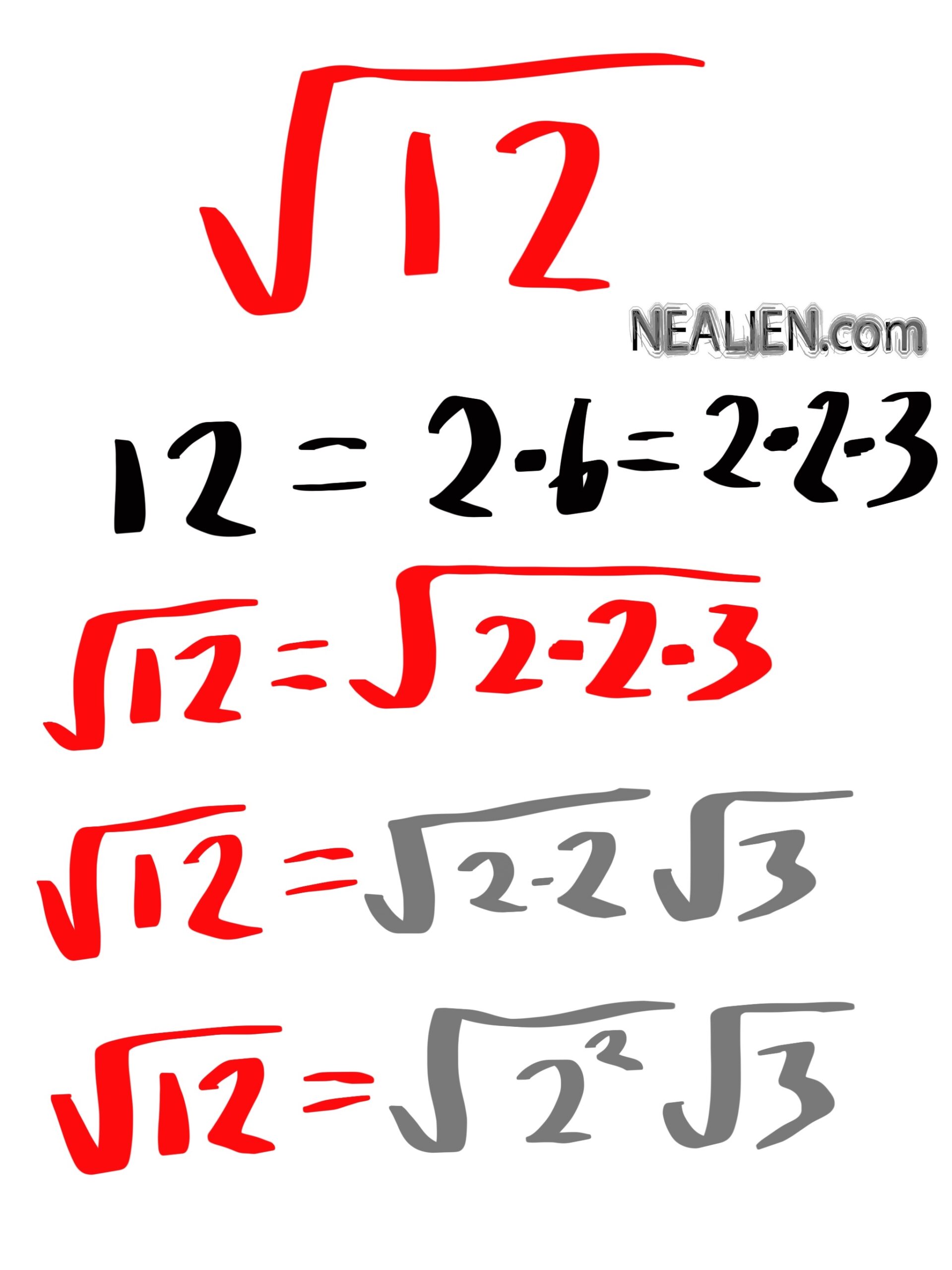Simplify the Square Root of 162 Easily and Effectively

The square root of 162 can be simplified by breaking down the number into its prime factors and simplifying further.

Step-by-Step Simplification

1. Prime factorize 162:
   • 162 ÷ 2 = 81
   • 81 ÷ 3 = 27
   • 27 ÷ 3 = 9
   • 9 ÷ 3 = 3
   • 3 ÷ 3 = 1
   Therefore, the prime factors of 162 are \(2 \times 3^4\).
2. Rewrite 162 as a product of its prime factors: \(162 = 2 \times 3^4\).
3. Use the property of square roots: \(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}\).
4. Simplify \(\sqrt{2 \times 3^4}\):
   • \(\sqrt{162} = \sqrt{2 \times 3^4}\)
   • \(\sqrt{2 \times 3^4} = \sqrt{2} \times \sqrt{3^4}\)
   • \(\sqrt{3^4} = 3^2 = 9\)
   Therefore, \(\sqrt{162} = 3^2 \times \sqrt{2} = 9\sqrt{2}\).

Final Simplified Form

The simplified form of the square root of 162 is:

\[\sqrt{162} = 9\sqrt{2}\]

This shows that the square root of 162 simplifies to 9 times the square root of 2.

The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 is 3, because 3 x 3 = 9. Square roots are fundamental in various fields of mathematics and have numerous practical applications.

In mathematical notation, the square root of a number x is written as √x. For instance, the square root of 162 is denoted as √162. Understanding square roots is essential for solving quadratic equations, performing algebraic manipulations, and working in geometry and trigonometry.

Here are some key points to understand about square roots:

• Positive and Negative Roots: Every positive number has two square roots: one positive and one negative. For example, √9 = 3 and √9 = -3.
• Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are called perfect squares because their square roots are whole numbers.
• Irrational Numbers: The square roots of non-perfect squares are irrational numbers. For instance, √2 and √162 are irrational because they cannot be expressed as a simple fraction.

When simplifying square roots, we aim to express the square root in its simplest form. This involves finding the prime factors of the number and pairing them to move outside the square root symbol.

Let's consider an example to illustrate the concept:

1. Identify the number you want to simplify the square root of, e.g., √162.
2. Find the prime factors of the number. For 162, the prime factors are 2 and 81 (since 162 = 2 x 81), and then further factoring 81 gives 3 x 3 x 3 x 3 (since 81 = 3 x 3 x 3 x 3).
3. Pair the prime factors to simplify: √162 = √(2 x 3 x 3 x 3 x 3) = 3 x 3√2 = 9√2.

Thus, the simplified form of √162 is 9√2. This simplification process is crucial for making calculations easier and more manageable in various mathematical problems.

Simplifying a square root involves breaking down the number inside the radical into its prime factors and then simplifying the expression to its simplest form. This process helps to make complex radical expressions more manageable and easier to work with. Here's how you can understand and simplify the square root of 162:

1. Prime Factorization:

   Start by finding the prime factors of 162. The prime factorization of 162 is:

   \[ 162 = 2 \times 3^4 \]

2. Group the Factors:

   Group the prime factors in pairs of equal factors. For 162, we have:

   \[ 162 = 2 \times (3^2 \times 3^2) \]

3. Simplify the Radical:

   Take one factor out of each pair of equal factors. This gives us:

   \[ \sqrt{162} = \sqrt{2 \times (3^2 \times 3^2)} = 3 \times 3 \times \sqrt{2} = 9\sqrt{2} \]

4. Final Simplified Form:

   The simplified form of the square root of 162 is:

   \[ \sqrt{162} = 9\sqrt{2} \]

This process of simplification is beneficial in various mathematical operations, as it reduces the complexity of the expression and makes it easier to work with in subsequent calculations.

To simplify the square root of 162, we need to break it down into its prime factors and identify any perfect squares. Here's a step-by-step process to understand the simplification:

1. Prime Factorization:

   First, we find the prime factors of 162. The prime factorization of 162 is:
   \[
   162 = 2 \times 3 \times 3 \times 3 \times 3 = 2 \times 3^4
   \]

2. Identify Perfect Squares:

   Next, we look for perfect squares within the prime factors. Here, \(3^4\) (which is 81) is a perfect square.

3. Rewrite the Expression:

   We can rewrite the square root of 162 by separating the perfect square from the non-perfect square:
   \[
   \sqrt{162} = \sqrt{2 \times 81} = \sqrt{2} \times \sqrt{81}
   \]

4. Simplify the Perfect Square:

   The square root of 81 is 9:
   \[
   \sqrt{81} = 9
   \]
   Therefore,
   \[
   \sqrt{162} = 9 \sqrt{2}
   \]

Thus, the simplified form of \(\sqrt{162}\) is \(9 \sqrt{2}\).

The prime factorization method is a systematic way of breaking down a number into its prime factors. To simplify the square root of 162 using this method, follow these detailed steps:

1. Find the prime factors of 162:

   Start by dividing 162 by the smallest prime number, which is 2:

   \(162 \div 2 = 81\)

   Next, divide 81 by the smallest prime number, which is 3:

   \(81 \div 3 = 27\)

   Continue dividing by 3:

   \(27 \div 3 = 9\)

   And again:

   \(9 \div 3 = 3\)

   Finally:

   \(3 \div 3 = 1\)

   So, the prime factors of 162 are:

   \(162 = 2 \times 3 \times 3 \times 3 \times 3\) or \(162 = 2 \times 3^4\)

2. Group the factors in pairs:

   Since we are simplifying the square root, we need to group the prime factors in pairs of the same number:

   \(162 = (3 \times 3) \times (3 \times 3) \times 2\)

3. Simplify the square root:

   Take one factor out of each pair and place them outside the radical. Since \(\sqrt{a \times a} = a\), this simplifies to:

   \(\sqrt{162} = \sqrt{(3 \times 3) \times (3 \times 3) \times 2} = 3 \times 3 \times \sqrt{2}\)

   This further simplifies to:

   \(\sqrt{162} = 9\sqrt{2}\)

4. Final Result:

   Thus, the simplified form of the square root of 162 is:

   \(\sqrt{162} = 9\sqrt{2}\)

In summary, by using the prime factorization method, we have expressed the square root of 162 in its simplest radical form as \(9\sqrt{2}\).

Simplifying the square root of 162 involves breaking it down into a product of simpler square roots. Here's a detailed step-by-step process:

1. Identify the prime factors of 162.

   Start by dividing 162 by the smallest prime number, which is 2:

   • 162 ÷ 2 = 81

   Next, find the prime factors of 81. Since 81 is an odd number, the next smallest prime factor is 3:

   • 81 ÷ 3 = 27
   • 27 ÷ 3 = 9
   • 9 ÷ 3 = 3
   • 3 ÷ 3 = 1

   Thus, the prime factorization of 162 is \( 2 \times 3^4 \).

2. Write 162 as a product of its prime factors inside the square root:

   \[ \sqrt{162} = \sqrt{2 \times 3^4} \]

3. Split the square root into the product of square roots:

   \[ \sqrt{162} = \sqrt{2} \times \sqrt{3^4} \]

4. Simplify the square root of the perfect square:

   \[ \sqrt{3^4} = \sqrt{(3^2)^2} = 3^2 = 9 \]

   Thus,

   \[ \sqrt{162} = \sqrt{2} \times 9 \]

5. Write the simplified form:

   \[ \sqrt{162} = 9 \sqrt{2} \]

Therefore, the simplified form of \(\sqrt{162}\) is \(9 \sqrt{2}\).

To help visualize the process of simplifying the square root of 162, we can use a combination of factor trees and geometric interpretation.

Prime Factorization Using a Factor Tree

A factor tree breaks down 162 into its prime factors:

• Start with the number 162.
• Divide by the smallest prime number 2 to get 81.
• Divide 81 by the next smallest prime, which is 3, to get 27.
• Divide 27 by 3 to get 9.
• Divide 9 by 3 to get 3.
• Divide 3 by 3 to get 1.

The prime factorization can be represented as a factor tree:

This shows:

\[ 162 = 2 \times 3 \times 3 \times 3 \times 3 = 2 \times 3^4 \]

Simplifying the Square Root

Using the prime factorization, we can simplify the square root of 162 as follows:

1. Write the number inside the square root as a product of its prime factors:

\[ \sqrt{162} = \sqrt{2 \times 3^4} \]

2. Separate the square root into the product of square roots:

\[ \sqrt{162} = \sqrt{2} \times \sqrt{3^4} \]

3. Simplify the square root of the perfect square:

\[ \sqrt{3^4} = 3^2 = 9 \]

4. Combine the simplified parts:

\[ \sqrt{162} = 9 \times \sqrt{2} \]

Geometric Interpretation

Imagine a square with an area of 162 square units. The side length of this square would be the square root of 162.

To visualize this:

• Consider that \(\sqrt{162}\) is approximately 12.7279, which is the side length of the square.
• When simplified, \(\sqrt{162}\) becomes \(9\sqrt{2}\).
• This means you can represent the side length as 9 units multiplied by \(\sqrt{2}\), showing how the larger area can be simplified into a product involving a simpler square root.

Summary

By using visual tools like factor trees and geometric representations, we can better understand and simplify the square root of 162 to \(9 \sqrt{2}\).

Simplifying square roots can be tricky, and it's easy to make mistakes. Here are some common pitfalls to watch out for when simplifying the square root of 162:

1. Incorrect Prime Factorization: Make sure to break down the number into the correct prime factors.

   For example, the correct prime factorization of 162 is:

   \[ 162 = 2 \times 3^4 \]

   Double-check each step of your factorization to ensure accuracy. Missing or incorrect factors can lead to the wrong simplification.

2. Not Simplifying the Square Root of Perfect Squares: Identify and simplify the square root of any perfect squares.

   In the case of 162:

   \[ \sqrt{162} = \sqrt{2 \times 3^4} \]

   Simplify the square root of \(3^4\) to \(3^2 = 9\). Then, write:

   \[ \sqrt{162} = 9 \times \sqrt{2} \]

   Failing to simplify this step can leave the expression in a more complex form than necessary.

3. Incorrect Separation of Square Roots: Separate the square roots accurately when dealing with products inside the radical.

   For example:

   \[ \sqrt{2 \times 3^4} = \sqrt{2} \times \sqrt{3^4} \]

   Incorrect separation might look like:

   \[ \sqrt{2 \times 3^4} \neq \sqrt{2 \times 3} \times \sqrt{3} \]

   This can lead to incorrect results and further complicate the simplification process.

4. Forgetting to Simplify the Radicand: Always simplify the expression under the square root as much as possible before applying other simplification steps.

   For instance:

   If given \(\sqrt{162}\), simplify \(162\) to its prime factors:

   \[ \sqrt{162} = \sqrt{2 \times 3^4} \]

   Then proceed with the simplification steps:

   \[ \sqrt{162} = \sqrt{2} \times 9 = 9\sqrt{2} \]

5. Assuming Non-Square Numbers Are Perfect Squares: Verify if the number inside the square root is a perfect square or can be simplified further.

   For example:

   \[ 162 \] is not a perfect square, but it can be simplified to:

   \[ 9 \times \sqrt{2} \]

   Always confirm the nature of the number to avoid incorrect assumptions.

By being mindful of these common mistakes, you can ensure accurate and efficient simplification of square roots like \(\sqrt{162}\).

Simplified square roots are not just an abstract mathematical concept; they have numerous practical applications across various fields. Here are some key areas where simplified square roots like \( \sqrt{162} = 9\sqrt{2} \) are useful:

1. Engineering and Construction

In engineering and construction, square roots are used to calculate dimensions and angles. For example:

• Area and Diagonal Calculations: The square root is essential when determining the length of a diagonal in a rectangular space. For instance, if a room's area is given and you need to find the diagonal, using the simplified square root helps in quick calculations.
• Stress and Load Calculations: Engineers use square roots to determine stress and load factors on structures, ensuring they are built safely and efficiently.

2. Physics

In physics, square roots are frequently used in formulas involving areas, volumes, and other measurements. Examples include:

• Wave Mechanics: Simplified square roots help in calculating the amplitude and frequency of waves, such as sound and light waves, where precise measurements are crucial.
• Energy Calculations: Formulas involving kinetic energy and potential energy often require the use of square roots. For example, in calculating the velocity of an object under gravitational force.

3. Computer Graphics

Simplified square roots are vital in computer graphics for rendering images and animations. Applications include:

• Distance Calculations: Calculating distances between points in 2D or 3D space often involves square roots. Simplified forms make these calculations faster and more efficient.
• Scaling and Transformation: Simplified square roots help in scaling objects and transforming coordinates, which are fundamental in creating realistic graphics.

4. Finance and Economics

In finance and economics, simplified square roots are used in various analytical models. Examples include:

• Risk Assessment: Calculating standard deviation, which measures the risk or volatility of an investment, involves square roots. Simplified forms make these calculations easier to manage.
• Compound Interest: Formulas for compound interest and growth rates often use square roots, especially in long-term projections.

5. Everyday Problem Solving

Simplified square roots also find applications in everyday life. Examples include:

• Cooking and Baking: When scaling recipes up or down, square roots help to maintain proportionality in ingredient quantities.
• Home Improvement: Calculating the amount of materials needed for a project, such as flooring or tiling, often involves square roots.

Understanding and simplifying square roots like \( \sqrt{162} = 9\sqrt{2} \) enables us to solve practical problems more efficiently in various fields, from science and engineering to finance and daily life.

To reinforce your understanding of simplifying square roots, try solving these practice problems. Each problem will help you apply the concepts discussed in this guide.

1. Problem 1: Simplify \(\sqrt{98}\)

   Break down 98 into its prime factors:

   \[ 98 = 2 \times 7^2 \]

   Simplify the square root:

   \[ \sqrt{98} = \sqrt{2 \times 7^2} = 7 \sqrt{2} \]

2. Problem 2: Simplify \(\sqrt{200}\)

   Find the prime factorization of 200:

   \[ 200 = 2^3 \times 5^2 \]

   Simplify the square root:

   \[ \sqrt{200} = \sqrt{2^3 \times 5^2} = 5 \times \sqrt{4 \times 2} = 10 \sqrt{2} \]

3. Problem 3: Simplify \(\sqrt{450}\)

   Prime factorize 450:

   \[ 450 = 2 \times 3^2 \times 5^2 \]

   Simplify the square root:

   \[ \sqrt{450} = \sqrt{2 \times 3^2 \times 5^2} = 3 \times 5 \times \sqrt{2} = 15 \sqrt{2} \]

4. Problem 4: Simplify \(\sqrt{242}\)

   Break down 242 into its prime factors:

   \[ 242 = 2 \times 11^2 \]

   Simplify the square root:

   \[ \sqrt{242} = \sqrt{2 \times 11^2} = 11 \sqrt{2} \]

5. Problem 5: Simplify \(\sqrt{288}\)

   Find the prime factors of 288:

   \[ 288 = 2^5 \times 3^2 \]

   Simplify the square root:

   \[ \sqrt{288} = \sqrt{2^5 \times 3^2} = \sqrt{(2^4 \times 2) \times 3^2} = 4 \times 3 \times \sqrt{2} = 12 \sqrt{2} \]

By working through these problems, you can practice breaking down numbers into their prime factors and simplifying their square roots. If you find these exercises helpful, try creating your own problems by choosing any number and following the steps to simplify its square root.

In this guide, we explored the process of simplifying the square root of 162 and delved into various related aspects. Let's summarize the key points we covered:

1. Introduction to Square Roots: We began by understanding what square roots represent and their importance in mathematics.

2. Understanding the Concept of Simplification: Simplifying square roots involves breaking down numbers into simpler, more manageable components, making calculations easier and more intuitive.

3. Breaking Down the Square Root of 162: We determined the prime factors of 162, which are \(2\) and \(3^4\). This step is crucial for the simplification process.

4. Prime Factorization Method: We used prime factorization to simplify \(\sqrt{162}\) into \(9\sqrt{2}\). This method helps to express the square root in its simplest form by identifying perfect squares within the radicand.

5. Step-by-Step Simplification Process: By following a clear, step-by-step approach, we simplified \(\sqrt{162}\) into \(9\sqrt{2}\), making the process understandable and replicable for other numbers.

6. Visual Representation and Explanation: Visual tools like factor trees and geometric interpretations provided intuitive ways to grasp the simplification of square roots, reinforcing the mathematical steps with concrete examples.

7. Common Mistakes to Avoid: We highlighted common errors such as incorrect factorization, improper separation of square roots, and neglecting to simplify the radicand. Recognizing these mistakes helps ensure accurate simplifications.

8. Practical Applications of Simplified Square Roots: Simplified square roots are widely used in various fields such as engineering, physics, computer graphics, finance, and everyday problem-solving, demonstrating their real-world relevance and utility.

9. Further Practice Problems: Practicing with additional problems allows you to apply the techniques learned and become proficient in simplifying square roots.

By mastering the simplification of square roots like \(\sqrt{162}\), you enhance your mathematical skills and gain the ability to solve complex problems with greater ease. Whether in academic pursuits, professional applications, or daily tasks, understanding how to simplify square roots equips you with valuable tools for efficient and accurate calculations.

Keep practicing and exploring, and you'll find that the principles of simplifying square roots are not only manageable but also incredibly useful in a variety of contexts.