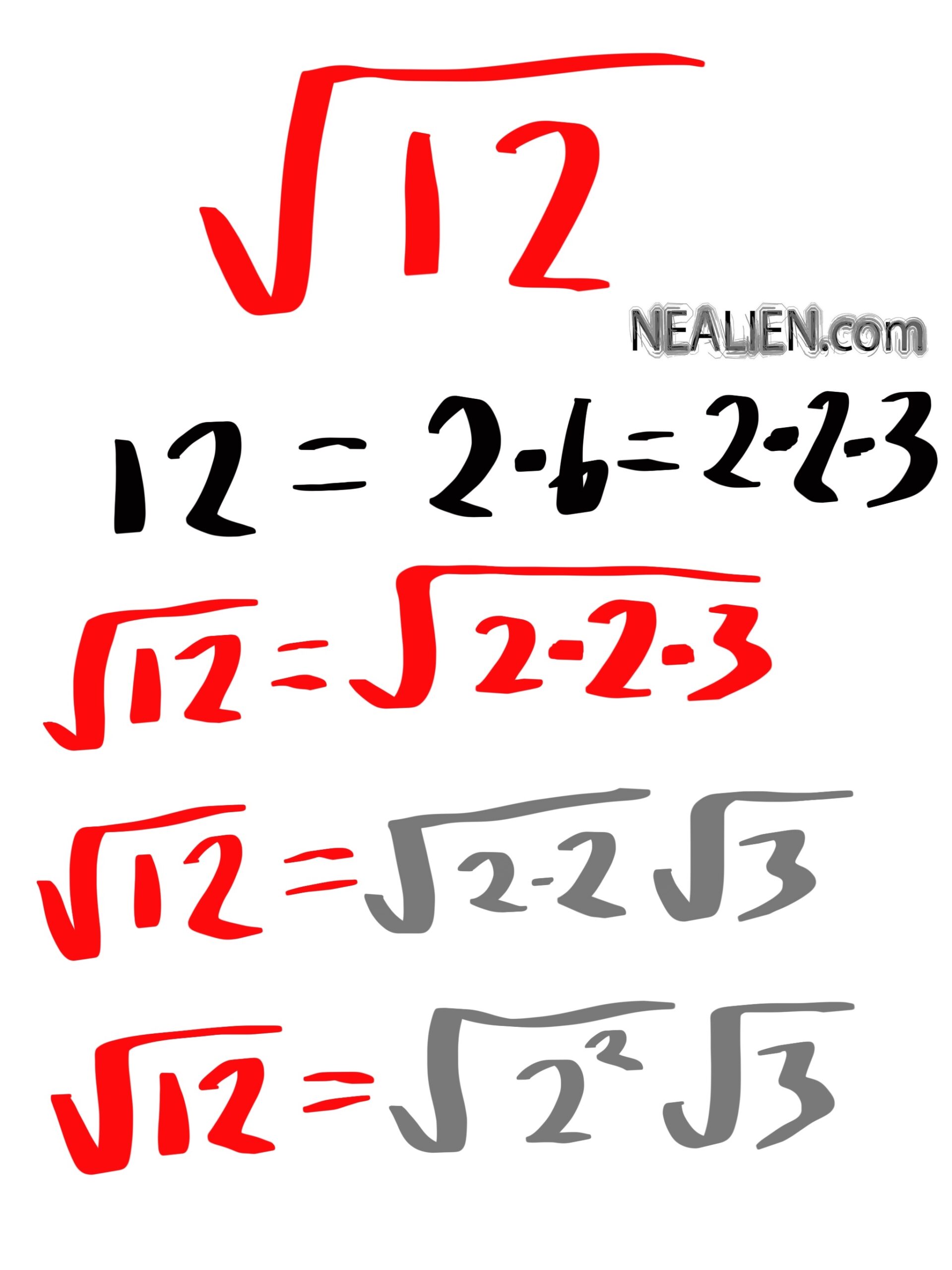Topic simplify square root expressions: Simplifying square root expressions can seem daunting, but with the right techniques and practice, it becomes a manageable and rewarding skill. This article will guide you through the essential methods and strategies, ensuring you gain confidence and proficiency in simplifying any square root expression you encounter.
Table of Content
- Simplifying Square Root Expressions
- Introduction
- Basic Concepts of Square Roots
- Methods of Simplifying Square Root Expressions
- Prime Factorization
- Pairing Prime Factors
- Combining and Simplifying Radicals
- Simplifying Square Roots with Variables
- Simplifying Expressions with Multiple Square Roots
- Techniques for Complex Denominators
- Simplifying Square Roots with Fractions
- Special Cases in Square Root Simplification
- Square Root Addition and Subtraction
- Using the Distributive Property
- Practice Problems and Solutions
- Common Mistakes to Avoid
- Advanced Simplification Techniques
- Application of Square Root Simplification in Algebra
- YOUTUBE: Video này giới thiệu cách đơn giản hóa căn bậc hai, giúp bạn hiểu và áp dụng vào các bài toán liên quan đến số mũ, căn bậc hai, và ký hiệu khoa học.
Simplifying Square Root Expressions
Simplifying square root expressions involves several techniques that help to make the expression more manageable. Below are some common methods and steps to simplify these expressions:
Basic Simplification
To simplify a square root expression, follow these steps:
- Find the prime factorization of the number under the square root.
- Pair the prime factors.
- Move each pair of prime factors out from under the square root.
For example, to simplify \(\sqrt{50}\):
\[
\sqrt{50} = \sqrt{2 \cdot 5 \cdot 5} = 5\sqrt{2}
\]
Simplifying Expressions with Variables
When simplifying square root expressions that include variables, treat the variables the same way you treat numbers:
\[
\sqrt{x^4y^2} = \sqrt{(x^2)^2(y)^2} = x^2y
\]
Rationalizing the Denominator
Sometimes it is necessary to eliminate a square root from the denominator of a fraction. This process is called rationalizing the denominator. Here’s how to do it:
- Multiply both the numerator and the denominator by the square root that is in the denominator.
- Simplify the resulting expression.
For example, to rationalize \(\frac{3}{\sqrt{5}}\):
\[
\frac{3}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{3\sqrt{5}}{5}
\]
Examples and Practice
- \(\sqrt{72} = \sqrt{36 \cdot 2} = 6\sqrt{2}\)
- \(\sqrt{18x^3} = \sqrt{9 \cdot 2x^3} = 3x\sqrt{2x}\)
- \(\frac{7}{\sqrt{3}} = \frac{7\sqrt{3}}{3}\)
- \(\frac{\sqrt{8}}{4} = \frac{2\sqrt{2}}{4} = \frac{\sqrt{2}}{2}\)
Special Cases
Sometimes, you may encounter square root expressions involving addition or subtraction. These expressions require different strategies:
- Combine like terms if possible.
- Use the distributive property if needed.
For example, to simplify \(\sqrt{45} + \sqrt{20}\):
\[
\sqrt{45} + \sqrt{20} = \sqrt{9 \cdot 5} + \sqrt{4 \cdot 5} = 3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5}
\]
Conclusion
Simplifying square root expressions is a valuable skill in algebra that involves understanding and applying prime factorization, rationalizing the denominator, and combining like terms. Practice these techniques to master simplifying any square root expression you encounter.

READ MORE:
Introduction
Welcome to our comprehensive guide on simplifying square root expressions. Square roots are a fundamental concept in mathematics, appearing in various fields such as algebra, geometry, and calculus. Simplifying square roots can make complex calculations more manageable and help in solving equations efficiently. In this guide, we will explore different techniques and methods to simplify square root expressions step-by-step.
Understanding how to simplify square roots is essential for students and professionals alike. Simplifying square root expressions involves breaking down the radicand (the number under the square root) into its prime factors and then applying various mathematical properties to reduce it to its simplest form. This process not only simplifies calculations but also provides a deeper understanding of the properties of numbers.
Throughout this guide, we will cover the following topics:
- Basic Concepts of Square Roots: Understanding the definition and properties of square roots.
- Methods of Simplifying Square Root Expressions: Various techniques to simplify square roots using prime factorization and other methods.
- Prime Factorization: Breaking down the radicand into its prime factors to simplify the expression.
- Pairing Prime Factors: Identifying and pairing prime factors to simplify the square root.
- Combining and Simplifying Radicals: Combining multiple square root expressions and simplifying them.
- Simplifying Square Roots with Variables: Techniques to simplify square roots that involve variables.
- Simplifying Expressions with Multiple Square Roots: Methods to handle expressions that contain more than one square root.
- Rationalizing the Denominator: Techniques to eliminate square roots from the denominator of a fraction.
- Techniques for Complex Denominators: Advanced methods to simplify expressions with complex denominators.
- Simplifying Square Roots with Fractions: Simplifying square roots that involve fractions.
- Special Cases in Square Root Simplification: Handling unique and special cases that arise in simplification.
- Square Root Addition and Subtraction: Methods to add and subtract square root expressions.
- Using the Distributive Property: Applying the distributive property to simplify expressions involving square roots.
- Practice Problems and Solutions: A set of practice problems with detailed solutions to reinforce the concepts learned.
- Common Mistakes to Avoid: Identifying and avoiding common errors in simplifying square roots.
- Advanced Simplification Techniques: Exploring more advanced techniques for simplifying square roots.
- Application of Square Root Simplification in Algebra: Applying the learned techniques in various algebraic contexts.
By the end of this guide, you will be equipped with the knowledge and skills to simplify square root expressions confidently and efficiently. Let's get started on this mathematical journey!
Basic Concepts of Square Roots
Understanding the basic concepts of square roots is essential for simplifying square root expressions effectively. A square root is a value that, when multiplied by itself, yields the original number. For instance, the square root of 9 is 3 because 3 multiplied by 3 equals 9. This can be expressed mathematically as:
\[ \sqrt{9} = 3 \] or \[ 3^2 = 9 \]
The symbol used to represent the square root is called the radical symbol (√), and the number under the radical symbol is known as the radicand. For example, in \(\sqrt{16}\), 16 is the radicand, and the expression represents the square root of 16, which is 4.
Key concepts related to square roots include:
- Perfect Squares: Numbers like 1, 4, 9, 16, and 25 are perfect squares because their square roots are whole numbers. For example, \(\sqrt{16} = 4\).
- Imperfect Squares: Numbers that are not perfect squares, such as 2, 3, or 5, have square roots that are irrational numbers. These cannot be expressed as a simple fraction and have non-repeating decimal expansions.
- Positive and Negative Roots: While the principal square root is always non-negative, every positive number actually has two square roots: one positive and one negative. For example, the square roots of 25 are 5 and -5.
Several methods can be used to find square roots, especially when dealing with imperfect squares:
- Prime Factorization: Breaking down a number into its prime factors and then pairing the factors. For example, to find the square root of 144, we factorize it as \(2 \times 2 \times 2 \times 2 \times 3 \times 3\), then pair the factors to get \(2 \times 2 \times 3 = 12\). Thus, \(\sqrt{144} = 12\).
- Repeated Subtraction Method: This involves subtracting successive odd numbers from the original number until zero is reached. The number of subtractions performed gives the square root. For example, for 25: \(25 - 1 = 24\), \(24 - 3 = 21\), \(21 - 5 = 16\), \(16 - 7 = 9\), \(9 - 9 = 0\). Thus, the square root of 25 is 5.
- Long Division Method: This method is useful for larger numbers and involves dividing the number into pairs of digits, then finding a number that squares to each pair.
Understanding these basic concepts and methods is crucial for mastering square root simplification and applying it in more complex mathematical problems.
Methods of Simplifying Square Root Expressions
There are several methods to simplify square root expressions. These methods help to break down the square roots into more manageable parts, making it easier to handle and compute. Here are the main methods:
-
Prime Factorization
Prime factorization involves breaking down the number under the square root into its prime factors. For example, to simplify \( \sqrt{72} \):
- Find the prime factors of 72: \( 72 = 2 \times 2 \times 2 \times 3 \times 3 \).
- Group the prime factors into pairs: \( 72 = (2 \times 2) \times (2 \times 3 \times 3) = 4 \times 18 \).
- Take one number from each pair out of the square root: \( \sqrt{72} = \sqrt{4 \times 18} = 2 \sqrt{18} \).
- Simplify further if possible: \( 18 = 2 \times 3 \times 3 \), so \( \sqrt{18} = 3 \sqrt{2} \), giving \( 2 \times 3 \sqrt{2} = 6 \sqrt{2} \).
-
Pairing Method
The pairing method involves identifying pairs of identical factors inside the square root and bringing them outside the square root. For example, to simplify \( \sqrt{50} \):
- Find the factors of 50: \( 50 = 2 \times 5 \times 5 \).
- Pair the factors: \( 50 = 5 \times 5 \times 2 \).
- Take one number from each pair out of the square root: \( \sqrt{50} = 5 \sqrt{2} \).
-
Simplifying Fractions
For expressions involving fractions, use the property \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). For example, to simplify \( \sqrt{\frac{16}{9}} \):
- Separate the fraction: \( \sqrt{\frac{16}{9}} = \frac{\sqrt{16}}{\sqrt{9}} \).
- Simplify the numerator and denominator: \( \frac{\sqrt{16}}{\sqrt{9}} = \frac{4}{3} \).
-
Combining Like Terms
Sometimes, you need to combine like terms after simplifying. For example, \( \sqrt{18} + \sqrt{50} \):
- Simplify each square root: \( \sqrt{18} = 3\sqrt{2} \) and \( \sqrt{50} = 5\sqrt{2} \).
- Combine the like terms: \( 3\sqrt{2} + 5\sqrt{2} = 8\sqrt{2} \).
By using these methods, you can simplify square root expressions more effectively, making complex calculations more manageable.
Prime Factorization
Prime factorization is a method used to break down a number into its basic prime components. This technique is essential in simplifying square roots. The process involves several steps to ensure that the square root expression is fully simplified.
Here are the steps to simplify square roots using prime factorization:
- Identify the number whose square root needs to be simplified.
- Break down the number into its prime factors.
- Group the prime factors into pairs.
- Move one factor from each pair outside the square root.
- Multiply the factors outside the square root to get the simplified result.
Let's look at some examples:
| Number | Prime Factorization | Simplification Process | Result |
|---|---|---|---|
| √72 | 72 = 2 × 2 × 2 × 3 × 3 |
|
6√2 |
| √180 | 180 = 2 × 2 × 3 × 3 × 5 |
|
6√5 |
| √50 | 50 = 2 × 5 × 5 |
|
5√2 |
Using prime factorization simplifies square root expressions effectively, making them easier to handle in various mathematical problems.

Pairing Prime Factors
Pairing prime factors is an essential step in simplifying square root expressions. This method involves identifying and grouping the prime factors of a number into pairs. Each pair of the same factor can be taken out of the square root as a single factor. Here is a step-by-step process for pairing prime factors:
- Prime Factorization:
First, decompose the number under the square root into its prime factors. For example, let's consider the number 72:
\[
72 = 2 \times 2 \times 2 \times 3 \times 3
\] - Group the Prime Factors:
Next, group the prime factors into pairs. Each pair will be represented as a square of the prime factor. For the example above, the pairs are:
\[
72 = (2 \times 2) \times (3 \times 3) \times 2 = 2^2 \times 3^2 \times 2
\] - Extract the Pairs:
For each pair of prime factors, extract one factor from the square root. The remaining unpaired factors stay inside the square root. Continuing with our example:
\[
\sqrt{72} = \sqrt{2^2 \times 3^2 \times 2} = 2 \times 3 \times \sqrt{2} = 6\sqrt{2}
\]
Let’s look at another example to solidify this concept. Consider the number 200:
- Prime Factorization:
\[
200 = 2 \times 2 \times 2 \times 5 \times 5
\] - Group the Prime Factors:
\[
200 = (2 \times 2) \times (5 \times 5) \times 2 = 2^2 \times 5^2 \times 2
\] - Extract the Pairs:
\[
\sqrt{200} = \sqrt{2^2 \times 5^2 \times 2} = 2 \times 5 \times \sqrt{2} = 10\sqrt{2}
\]
By using this method, you can simplify any square root expression involving integers. Remember, pairing prime factors and extracting them is a straightforward way to handle square roots efficiently.
Combining and Simplifying Radicals
Simplifying and combining radicals involves breaking down the radicand (the number inside the radical) into its prime factors and then applying the product rule for radicals. This process can be done step-by-step as follows:
Step-by-Step Guide
-
Identify and factor the radicand: Break down the number inside the radical into its prime factors.
For example, consider the expression \( \sqrt{72} \):
- 72 can be factored into \( 2^3 \cdot 3^2 \).
-
Group the factors: Pair the prime factors to simplify the radical.
Using the example \( \sqrt{72} \), we group the factors as follows:
- \( 72 = 2^2 \cdot 2 \cdot 3^2 \)
- Therefore, \( \sqrt{72} = \sqrt{(2^2 \cdot 3^2 \cdot 2)} = \sqrt{(4 \cdot 9 \cdot 2)} = \sqrt{(36 \cdot 2)} \).
-
Apply the product rule for radicals: Use the property \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \) to separate the factors.
Continuing with \( \sqrt{72} \):
- \( \sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} \).
- Since \( \sqrt{36} = 6 \), we get \( 6\sqrt{2} \).
Examples of Combining Radicals
Combining radicals follows the same rules as combining like terms in algebra. Radicals can be combined if they have the same radicand.
-
Addition of Radicals:
For example, \( 3\sqrt{2} + 4\sqrt{2} \) can be combined because the radicand is the same:
- \( 3\sqrt{2} + 4\sqrt{2} = (3 + 4)\sqrt{2} = 7\sqrt{2} \).
-
Subtraction of Radicals:
For example, \( 5\sqrt{3} - 2\sqrt{3} \) can be combined similarly:
- \( 5\sqrt{3} - 2\sqrt{3} = (5 - 2)\sqrt{3} = 3\sqrt{3} \).
Practice Problems
Try simplifying and combining the following radical expressions:
- Simplify \( \sqrt{50} \).
- Combine \( 2\sqrt{18} + 3\sqrt{8} \).
Solutions:
-
\( \sqrt{50} = \sqrt{25 \cdot 2} = 5\sqrt{2} \).
-
First, simplify each radical:
- \( 2\sqrt{18} = 2\sqrt{9 \cdot 2} = 2 \cdot 3\sqrt{2} = 6\sqrt{2} \).
- \( 3\sqrt{8} = 3\sqrt{4 \cdot 2} = 3 \cdot 2\sqrt{2} = 6\sqrt{2} \).
Then, combine the like terms:
- \( 6\sqrt{2} + 6\sqrt{2} = 12\sqrt{2} \).
Conclusion
Combining and simplifying radicals can greatly simplify expressions and make them easier to work with. By factoring the radicand, applying the product rule, and combining like terms, complex radical expressions can be simplified effectively.
Simplifying Square Roots with Variables
When simplifying square roots that contain variables, we can follow a systematic approach to ensure accuracy. Here's a step-by-step guide:
- Identify Perfect Squares: Look for variable terms that can be rewritten as perfect squares. For example, \( x^4 \) can be written as \( (x^2)^2 \).
- Separate the Radicals: Use the property \( \sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} \) to split the square root into simpler parts. For example, \( \sqrt{9x^6} \) can be split into \( \sqrt{9} \cdot \sqrt{x^6} \).
- Simplify Each Part: Simplify the numerical part and the variable part separately. For the example \( \sqrt{9x^6} \):
- Simplify the numerical part: \( \sqrt{9} = 3 \)
- Simplify the variable part: \( \sqrt{x^6} = x^3 \) (because \( x^6 = (x^3)^2 \))
- Combine the Results: Multiply the simplified numerical part and the variable part to get the final result. In our example, \( \sqrt{9x^6} = 3x^3 \).
Here are a few more examples to illustrate the process:
Example 1: Simplify \( \sqrt{16y^8} \)
- Separate the radicals: \( \sqrt{16} \cdot \sqrt{y^8} \)
- Simplify each part: \( \sqrt{16} = 4 \) and \( \sqrt{y^8} = y^4 \) (because \( y^8 = (y^4)^2 \))
- Combine the results: \( \sqrt{16y^8} = 4y^4 \)
Example 2: Simplify \( \sqrt{49x^{10}y^6} \)
- Separate the radicals: \( \sqrt{49} \cdot \sqrt{x^{10}} \cdot \sqrt{y^6} \)
- Simplify each part: \( \sqrt{49} = 7 \), \( \sqrt{x^{10}} = x^5 \) (because \( x^{10} = (x^5)^2 \)), and \( \sqrt{y^6} = y^3 \) (because \( y^6 = (y^3)^2 \))
- Combine the results: \( \sqrt{49x^{10}y^6} = 7x^5y^3 \)
These steps can be applied to any square root expression containing variables, helping to simplify complex expressions into more manageable forms.
Simplifying Expressions with Multiple Square Roots
Simplifying expressions with multiple square roots can be achieved by using the product rule, which states that the square root of a product is the product of the square roots. Here is a detailed, step-by-step guide to simplify such expressions:
-
Combine the Radicands:
When dealing with multiple square roots, start by combining the radicands (the numbers inside the square roots) under a single radical sign. For example, to simplify
-
Factor the Combined Radicand:
Next, factor the combined radicand into its prime factors. For example,
90 2*3*3*5 -
Pair and Simplify:
Look for pairs of prime factors inside the radical. Each pair can be simplified and pulled out of the square root. For example,
2*3*3*5 3 10 -
Example Problem:
Let's simplify
18 2 18*2 36 - Simplify to get
6
By following these steps, you can simplify any expression involving multiple square roots, ensuring the expression is as simplified as possible.

Techniques for Complex Denominators
When simplifying square root expressions with complex denominators, it's essential to eliminate the radicals from the denominator. Here are detailed steps and techniques to achieve this:
1. Rationalizing Denominators with Single Terms
To rationalize a denominator with a single term involving a square root:
- Identify the radical in the denominator. For example, in the expression \(\frac{1}{\sqrt{5}}\).
- Multiply both the numerator and the denominator by the same radical to eliminate the square root. In this case, multiply by \(\frac{\sqrt{5}}{\sqrt{5}}\):
- The result is a rationalized denominator: \(\frac{\sqrt{5}}{5}\).
\(\frac{1}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{5}\).
2. Rationalizing Denominators Using the Conjugate
When the denominator is a binomial involving square roots, use the conjugate to rationalize it. The conjugate of a binomial \(a \pm \sqrt{b}\) is \(a \mp \sqrt{b}\).
- Identify the binomial denominator. For example, in \(\frac{1}{\sqrt{3} + 2}\).
- Multiply the numerator and the denominator by the conjugate of the denominator. Here, the conjugate of \(\sqrt{3} + 2\) is \(\sqrt{3} - 2\):
- The result is a simplified expression: \(-\sqrt{3} + 2\).
\(\frac{1}{\sqrt{3} + 2} \cdot \frac{\sqrt{3} - 2}{\sqrt{3} - 2} = \frac{\sqrt{3} - 2}{(\sqrt{3})^2 - (2)^2} = \frac{\sqrt{3} - 2}{3 - 4} = \frac{\sqrt{3} - 2}{-1} = -(\sqrt{3} - 2)\).
3. Rationalizing Higher Order Roots
For higher-order roots, such as fourth roots, ensure the radicand becomes a perfect power matching the root's order:
- Identify the higher-order root in the denominator. For example, in \(\frac{3\sqrt[4]{11}}{\sqrt[4]{2}}\).
- Multiply by a term that will make the denominator a perfect power. Here, multiply by \(\frac{\sqrt[4]{8}}{\sqrt[4]{8}}\):
- The denominator is now rationalized: \(\frac{3\sqrt[4]{88}}{2}\).
\(\frac{3\sqrt[4]{11}}{\sqrt[4]{2}} \cdot \frac{\sqrt[4]{8}}{\sqrt[4]{8}} = \frac{3\sqrt[4]{88}}{\sqrt[4]{16}} = \frac{3\sqrt[4]{88}}{2}\).
These techniques help in simplifying expressions with complex denominators, making them more manageable and easier to understand.
Simplifying Square Roots with Fractions
When simplifying square roots with fractions, the process involves simplifying the square roots and then rationalizing the denominator. Let's break down the steps in detail:
-
Simplify the Square Roots
Start by simplifying the square roots in both the numerator and the denominator. For instance:
\[\frac{\sqrt{72}}{\sqrt{18}}\]
Simplify each square root:
\[\sqrt{72} = \sqrt{36 \times 2} = 6\sqrt{2}\]
\[\sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2}\]
-
Simplify the Fraction
Once the square roots are simplified, reduce the fraction if possible:
\[\frac{6\sqrt{2}}{3\sqrt{2}} = \frac{6}{3} = 2\]
-
Rationalize the Denominator (if needed)
If the denominator still contains a square root, rationalize it by multiplying the numerator and the denominator by the conjugate of the denominator:
For example:
\[\frac{5}{\sqrt{3}} = \frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3}\]
Let's look at another example for clarity:
Example: Simplify \[\frac{4}{\sqrt{8}}\]
-
Simplify the square root:
\[\sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2}\]
-
Rewrite the fraction:
\[\frac{4}{\sqrt{8}} = \frac{4}{2\sqrt{2}} = \frac{2}{\sqrt{2}}\]
-
Rationalize the denominator:
\[\frac{2}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}} = \frac{2\sqrt{2}}{2} = \sqrt{2}\]
With practice, simplifying square roots with fractions will become straightforward and manageable. Remember to always simplify the square roots first, then rationalize the denominator to ensure the fraction is in its simplest form.
Special Cases in Square Root Simplification
Simplifying square root expressions can often involve special cases that require particular attention. These cases may include dealing with fractions, expressions involving variables, and expressions under certain conditions. Below are detailed steps and examples for handling these special cases.
Square Roots of Perfect Squares
When the radicand (the number under the square root sign) is a perfect square, the square root simplifies to an integer.
- \(\sqrt{36} = 6\)
- \(\sqrt{144} = 12\)
Square Roots of Fractions
To simplify the square root of a fraction, use the quotient rule: \(\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\).
- \(\sqrt{\frac{25}{4}} = \frac{\sqrt{25}}{\sqrt{4}} = \frac{5}{2}\)
- \(\sqrt{\frac{49}{9}} = \frac{\sqrt{49}}{\sqrt{9}} = \frac{7}{3}\)
Expressions with Variables
When simplifying square roots involving variables, consider the exponent of the variable:
- If the exponent is even, the square root is the variable raised to half the exponent: \(\sqrt{x^6} = x^3\).
- If the exponent is odd, separate it into even and odd parts: \(\sqrt{x^5} = \sqrt{x^4 \cdot x} = x^2 \sqrt{x}\).
Examples:
- \(\sqrt{a^4} = a^2\)
- \(\sqrt{a^6b^{10}} = a^3b^5\)
- \(\sqrt{y^5} = y^2 \sqrt{y}\)
Square Roots Involving Negative Numbers
Square roots of negative numbers are not real numbers. They are expressed in terms of imaginary numbers using \(i\), where \(i = \sqrt{-1}\).
- \(\sqrt{-4} = 2i\)
- \(\sqrt{-9} = 3i\)
Complex Radicands
For expressions that are more complex, such as those involving multiple terms or factors, use the product rule: \(\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\).
- \(\sqrt{75} = \sqrt{25 \cdot 3} = 5\sqrt{3}\)
- \(\sqrt{50x^2 y^3 z} = \sqrt{25x^2 \cdot 2y^3 \cdot z} = 5x y\sqrt{2y z}\)
Rationalizing the Denominator
When a fraction has a square root in the denominator, rationalize it by multiplying the numerator and the denominator by the conjugate or by the square root itself:
- \(\frac{1}{\sqrt{2}} = \frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)
- \(\frac{3}{\sqrt{5} + 2} = \frac{3}{\sqrt{5} + 2} \cdot \frac{\sqrt{5} - 2}{\sqrt{5} - 2} = \frac{3(\sqrt{5} - 2)}{5 - 4} = 3(\sqrt{5} - 2)\)
These special cases in square root simplification require careful application of mathematical rules and properties to achieve the simplest form of the expression. Practice with these methods will improve your ability to handle complex square root problems efficiently.
Square Root Addition and Subtraction
When adding or subtracting square root expressions, it is essential that the radicands (the numbers under the square root) and the index (the type of root, e.g., square root) are the same. This is similar to combining like terms in algebra.
Steps for Adding and Subtracting Square Roots
- Simplify each radical: Before adding or subtracting, ensure that each square root is in its simplest form. For example, simplify \(\sqrt{18}\) to \(3\sqrt{2}\).
- Combine like terms: Only square roots with the same radicand can be added or subtracted. For instance, \(2\sqrt{3}\) and \(5\sqrt{3}\) can be combined to make \(7\sqrt{3}\).
Examples
- Example 1: Simplify \(\sqrt{2} + 3\sqrt{2}\)
Since both terms have the same radicand (\(\sqrt{2}\)), we can combine them: \(1\sqrt{2} + 3\sqrt{2} = 4\sqrt{2}\).
- Example 2: Simplify \(5\sqrt{12} + 2\sqrt{3}\)
First, simplify \(\sqrt{12}\) to \(2\sqrt{3}\):
- \(5\sqrt{12} = 5\sqrt{4 \times 3} = 5 \times 2\sqrt{3} = 10\sqrt{3}\)
- Now, combine \(10\sqrt{3} + 2\sqrt{3} = 12\sqrt{3}\)
- Example 3: Simplify \(3\sqrt{8} + 5\sqrt{2}\)
First, simplify \(\sqrt{8}\) to \(2\sqrt{2}\):
- \(3\sqrt{8} = 3\sqrt{4 \times 2} = 3 \times 2\sqrt{2} = 6\sqrt{2}\)
- Now, combine \(6\sqrt{2} + 5\sqrt{2} = 11\sqrt{2}\)
- Example 4: Simplify \(20\sqrt{72a^3b^4c} - 14\sqrt{8a^3b^4c}\)
Rewrite each term with the same radicand:
- \(20\sqrt{72a^3b^4c} = 20 \times 6a^2b^2\sqrt{2ac} = 120a^2b^2\sqrt{2ac}\)
- \(14\sqrt{8a^3b^4c} = 14 \times 2a^2b^2\sqrt{2ac} = 28a^2b^2\sqrt{2ac}\)
- Now, combine \(120a^2b^2\sqrt{2ac} - 28a^2b^2\sqrt{2ac} = 92a^2b^2\sqrt{2ac}\)
Always ensure to simplify each radical expression before performing addition or subtraction. This process helps in identifying like terms that can be combined to simplify the expression further.

Using the Distributive Property
The distributive property is a fundamental algebraic property used to simplify expressions by distributing a single term across terms inside parentheses. It is expressed as \( a(b + c) = ab + ac \). This property is particularly useful when dealing with square root expressions.
Here are some steps to use the distributive property for simplifying square root expressions:
- Identify the terms: Recognize the terms inside and outside the parentheses that need to be distributed.
- Distribute the term: Multiply the term outside the parentheses by each term inside the parentheses.
- Simplify: Simplify the resulting expression, if possible.
Let's look at some examples:
- Example 1: Simplify \( 2(\sqrt{4} + \sqrt{10}) \)
- Distribute \( 2 \) across \( \sqrt{4} \) and \( \sqrt{10} \): \( 2 \times \sqrt{4} + 2 \times \sqrt{10} \)
- Simplify the square roots: \( 2 \times 2 + 2 \times \sqrt{10} \)
- Result: \( 4 + 2\sqrt{10} \)
- Example 2: Simplify \( \sqrt{5}(\sqrt{8} + \sqrt{10}) \)
- Distribute \( \sqrt{5} \) across \( \sqrt{8} \) and \( \sqrt{10} \): \( \sqrt{5} \times \sqrt{8} + \sqrt{5} \times \sqrt{10} \)
- Combine the square roots: \( \sqrt{40} + \sqrt{50} \)
- Simplify the square roots: \( 2\sqrt{10} + 5\sqrt{2} \)
- Example 3: Simplify \( \sqrt{3}(\sqrt{9} + \sqrt{21}) \)
- Distribute \( \sqrt{3} \) across \( \sqrt{9} \) and \( \sqrt{21} \): \( \sqrt{3} \times \sqrt{9} + \sqrt{3} \times \sqrt{21} \)
- Combine the square roots: \( \sqrt{27} + \sqrt{63} \)
- Simplify the square roots: \( 3\sqrt{3} + 3\sqrt{7} \)
Using the distributive property can simplify complex square root expressions and make it easier to handle and solve them in algebraic problems.
Practice Problems and Solutions
Practice problems are essential for mastering the simplification of square root expressions. Here are a few problems and their step-by-step solutions to help you understand the process.
Problem 1: Simplify \( \sqrt{72} \)
- Factor 72 into its prime factors: \( 72 = 2^3 \times 3^2 \).
- Group the prime factors into pairs: \( 72 = (2^2 \times 3^2) \times 2 \).
- Take out the pairs from under the square root: \( \sqrt{72} = \sqrt{(2^2 \times 3^2) \times 2} = 2 \times 3 \times \sqrt{2} \).
- Simplify: \( \sqrt{72} = 6\sqrt{2} \).
Problem 2: Simplify \( \sqrt{50x^2y^3} \)
- Factor the expression into its prime factors: \( 50x^2y^3 = 2 \times 5^2 \times x^2 \times y^2 \times y \).
- Group the prime factors into pairs: \( 50x^2y^3 = (5^2 \times x^2 \times y^2) \times 2y \).
- Take out the pairs from under the square root: \( \sqrt{50x^2y^3} = \sqrt{(5^2 \times x^2 \times y^2) \times 2y} = 5xy \sqrt{2y} \).
- Simplify: \( \sqrt{50x^2y^3} = 5xy\sqrt{2y} \).
Problem 3: Simplify \( \sqrt{\frac{18}{2}} \)
- Simplify the fraction under the square root: \( \frac{18}{2} = 9 \).
- Take the square root: \( \sqrt{9} = 3 \).
Problem 4: Simplify \( \sqrt{8} + \sqrt{18} \)
- Factor the square roots: \( \sqrt{8} = \sqrt{4 \times 2} = 2\sqrt{2} \) and \( \sqrt{18} = \sqrt{9 \times 2} = 3\sqrt{2} \).
- Combine like terms: \( 2\sqrt{2} + 3\sqrt{2} = 5\sqrt{2} \).
Problem 5: Rationalize the denominator of \( \frac{5}{\sqrt{3}} \)
- Multiply the numerator and denominator by \( \sqrt{3} \): \( \frac{5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{5\sqrt{3}}{3} \).
- Simplify the expression: \( \frac{5\sqrt{3}}{3} \).
Practice More
Try the following problems on your own and check the solutions provided:
- Simplify \( \sqrt{200} \).
- Simplify \( \sqrt{48x^4} \).
- Simplify \( \sqrt{\frac{45}{5}} \).
- Combine \( \sqrt{27} + \sqrt{12} \).
- Rationalize the denominator of \( \frac{4}{\sqrt{5}} \).
With practice, you'll become more confident in simplifying square root expressions!
Common Mistakes to Avoid
When simplifying square root expressions, there are several common mistakes that students often make. Understanding and avoiding these mistakes can help ensure accurate and efficient simplification of square roots.
- Ignoring Prime Factorization: Always perform prime factorization first to break down the number inside the square root into its prime factors. This helps in identifying pairs of prime numbers for simplification.
- Forgetting to Simplify Completely: Ensure that the square root expression is simplified as much as possible. Sometimes, students stop too early without fully reducing the expression.
- Incorrect Pairing of Factors: When pairing prime factors, make sure to correctly identify and pair them. Mistakes in pairing can lead to incorrect simplification.
- Not Rationalizing the Denominator: If there is a square root in the denominator, always rationalize it by multiplying both the numerator and the denominator by the appropriate value to eliminate the square root from the denominator.
- Misapplying Properties of Radicals: Be careful when applying properties of radicals such as the product rule \( \sqrt{a} \cdot \sqrt{b} = \sqrt{ab} \) and the quotient rule \( \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \). These properties only hold under certain conditions.
- Errors with Variables: When simplifying square roots that include variables, remember to treat variables just like numbers, applying the same rules for pairing and simplifying.
- Omitting Absolute Value: For even roots, such as square roots, when variables are involved, consider the absolute value to ensure the result is non-negative. For example, \( \sqrt{x^2} = |x| \).
By being mindful of these common mistakes, you can improve your accuracy in simplifying square root expressions and develop a stronger understanding of the underlying concepts.
Advanced Simplification Techniques
In this section, we will explore advanced techniques for simplifying square root expressions. These methods go beyond basic factorization and can be particularly useful for more complex problems.
Using the Product Rule
The product rule for square roots states that for any non-negative numbers \(a\) and \(b\), the square root of their product is the product of their square roots:
\[\sqrt{ab} = \sqrt{a} \cdot \sqrt{b}\]
Example:
\[\sqrt{72} = \sqrt{36 \cdot 2} = \sqrt{36} \cdot \sqrt{2} = 6\sqrt{2}\]
Combining Multiple Radicals
When dealing with the product of multiple square roots, you can combine them into a single radical and then simplify:
Example:
\[\sqrt{12} \cdot \sqrt{3} = \sqrt{12 \cdot 3} = \sqrt{36} = 6\]
Using the Quotient Rule
The quotient rule allows you to simplify the square root of a fraction by separating the numerator and the denominator:
\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}\]
Example:
\[\sqrt{\frac{50}{2}} = \frac{\sqrt{50}}{\sqrt{2}} = \frac{5\sqrt{2}}{\sqrt{2}} = 5\]
Simplifying Expressions with Variables
To simplify square roots with variables, factor out the squares from under the radical:
Example:
\[\sqrt{50x^2y^3z} = \sqrt{25 \cdot 2 \cdot x^2 \cdot y^2 \cdot y \cdot z} = 5xy\sqrt{2yz}\]
Simplifying Sums and Differences
When simplifying sums or differences of square roots, first simplify each term and then combine like radicals:
Example:
\[2\sqrt{12} + 9\sqrt{3} = 2 \cdot 2\sqrt{3} + 9\sqrt{3} = 4\sqrt{3} + 9\sqrt{3} = 13\sqrt{3}\]
Dealing with Higher Powers
For expressions involving higher powers under the radical, use the following approach:
Example:
\[\sqrt{81a^4b^4 \cdot 2a} = \sqrt{81a^4b^4} \cdot \sqrt{2a} = 9a^2b^2\sqrt{2a}\]
Complex Expressions
For more complex expressions, break them down into simpler parts, apply the relevant rules, and then recombine:
Example:
\[\sqrt{20} \cdot \sqrt{5}\sqrt{2} = \sqrt{20 \cdot 5 \cdot 2} = \sqrt{200} = \sqrt{100 \cdot 2} = 10\sqrt{2}\]
Practice Problems
- Simplify \(\sqrt{45} + \sqrt{80}\)
- Simplify \(\sqrt{75x^2y^4} - \sqrt{27x^2y^4}\)
- Simplify \(\sqrt{\frac{8x^3}{2x}}\)

Application of Square Root Simplification in Algebra
Simplifying square root expressions is an essential skill in algebra, allowing us to solve various real-world problems. Here are some key applications:
-
Geometry:
Square root simplification is often used to find the length of the sides of squares and other geometric shapes. For example, if the area of a square is given, the side length can be found by taking the square root of the area.
Example: If the area of a square is \(A = 370 \, \text{sq ft}\), the side length \(s\) is given by:
\[\sqrt{370} \approx 19.2 \, \text{ft}\]
-
Physics:
In physics, the time it takes for an object to fall to the ground is calculated using square roots. The formula to determine the time \(t\) is:
\[t = \frac{\sqrt{h}}{4}\]
where \(h\) is the height from which the object is dropped. For example, if an object is dropped from a height of 64 feet, the time to reach the ground is:
\[t = \frac{\sqrt{64}}{4} = \frac{8}{4} = 2 \, \text{seconds}\]
-
Accident Investigations:
Police use the length of skid marks to determine the speed of vehicles before braking. The speed \(v\) can be estimated using the formula:
\[v = \sqrt{24d}\]
where \(d\) is the length of the skid marks. For example, if the skid marks are 190 feet long, the speed of the car is:
\[v = \sqrt{24 \times 190} \approx 67.5 \, \text{mph}\]
Understanding and applying square root simplification in these contexts not only helps in solving algebraic problems but also in interpreting real-world scenarios effectively.
Video này giới thiệu cách đơn giản hóa căn bậc hai, giúp bạn hiểu và áp dụng vào các bài toán liên quan đến số mũ, căn bậc hai, và ký hiệu khoa học.
Đơn giản hóa căn bậc hai | Số mũ, căn bậc hai, và ký hiệu khoa học | Toán cơ bản | Khan Academy
READ MORE:
Video này hướng dẫn cách đơn giản hóa căn bậc hai, giúp bạn nắm vững các kỹ thuật cần thiết để giải các bài toán về căn bậc hai một cách hiệu quả.
Cách Đơn Giản Hóa Căn Bậc Hai